一元一次方程
例题1: 这是北师大版小学六年级上册课本95页的一道解方程练习题:
大家可以先口算一下,这道题里面的x的值为200
接下来我们用python来实现,代码如下,每一句代码后面都写有解释语:
# 一元一次方程 x = sy.symbols("x") # 申明未知数"x" a = sy.solve((x+(1/5)*x-240),[x]) # 写入需要解的方程体 print(a)
大家应该注意到了,在写入方程体的时候,(上面的第三行代码)我们并没有原封不动的将原方程写进去,而是换了一种写法,将等号右边的数移到了等号左边(当然,移动的过程中注意要变号哦!)然后将等号丢弃,最后变成了一个式子。这个是我们的一个固定写法,大家记住就可以了。
注意:注意!!在数学里面数字和未知数相乘时中间可以不加任何符号,比如2x就代表2乘以x,但在计算机里,乘法必须写成*乘的形式。比如2*x,而不能直接写出2x,此处一定要注意!
这是运行后的结果:
大家可以看到,结果被一对大括号包裹着,冒号前是要求的未知数,冒号后即是程序运行后得出的结果。
我们的计算机还是很聪明的,是吧!
例题2: 接下来,我们再来尝试一下分式方程:
以下为2018成都市的中考数学真题A卷第8题:
用同样的程序逻辑,填好我们要求的方程,代码如下:
x = sy.symbols("x")
a = sy.solve([(x+1)/x+1/(x-2)-1],[x])
print(a)
#{x: 1}
运行结果:
二元一次方程
例题3: 接下来我们来试一下两个未知数的
这是北师大版初中八年级上册课本132页的一道练习题:
用python来实现,
# 二元一次方程 x,y = sy.symbols("x y") a = sy.solve([3*x-2*y-3,x+2*y-5],[x,y]) print(a) # {x: 2, y: 3/2}
运行结果:
所以正确答案为:C答案
以下为2018成都市的中考数学真题B卷第21题:
用Python实现:
x,y = sy.symbols("x y") a = sy.solve([x + y - 0.2,x + 3*y -1],[x,y]) x = a[x] y = a[y] re = x**2+4*x*y +4*y**2 print(re)
注意:
- 不要省略乘号“*”
- “**”代表乘方
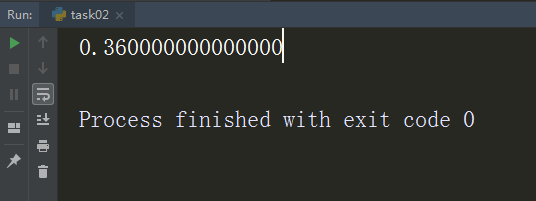
运行结果截图:
多元线性方程组求解
求解线性方程组比较简单,只需要用到一个函数(scipy.linalg.solve)就可以了。
import numpy as np from scipy.linalg import solve #输出系数矩阵 a=np.array([[3,1,-2],[1,-1,4],[2,0,3]]) #值 b=np.array([5,-2,2.5]) #计算 x=solve(a,b) #打印结果 print(x)
[0.5 4.5 0.5]
sympy 数学方程求解
SymPy是比较强大的,可以做到符号的化简,求值等。SymPy是符号数学的Python库。它的目标是成为一个全功能的计算机代数系统,同时保持代码简洁、易于理解和扩展。 SymPy完全是用Python写的,并不需要外部的库。
可以做到先设置变量,然后打印不需要设置值的功能,例如:在我们日常书写中print(x+y)是会报错的,然而使用了如下就不会报错了:
from sympy import * x,y= symbols('x,y') print(x + y+x+y)
2*x + 2*y
公式与代码之间转换:
- 加号 +
- 减号 -
- 除号 /
- 乘号 *
- 指数 **
- 对数 log()
- e的指数次幂 exp()