深入理解计算机系统——实验（二）Data Lab（附解释）

2020-4-18更新

有朋友对下列第5个函数bang中我的分析提出了质疑，隔了一年多我也不大记得了。

首先关于补码（Two's complement），给出wikipedia中的定义：

Two's complement is a mathematical operation on binary numbers, and is an example of a radix complement. It is used in computing as a method of signed number representation.

The two's complement of an N-bit number is defined as its complement with respect to . For instance, for the three-bit number 010, the two's complement is 110, because 010 + 110 = 1000. The two's complement is calculated by inverting the digits and adding one.

wikipedia中提到了它的歧义性：

Potential ambiguities of terminology

The term two's complement can mean either a number format or a mathematical operator. For example, 0111 represents decimal 7 in two's-complement notation, but the two's complement of 7 in a 4-bit register is actually the "1001" bit string (the same as represents 9 = 24 − 7 in unsigned arithmetics) which is the two's complement representation of −7. The statement "convert x to two's complement" may be ambiguous, since it could describe either the process of representing x in two's-complement notation without changing its value, or the calculation of the two's complement, which is the arithmetic negative of x if two's complement representation is used.

附图表一张：

但是我百度到，绝大多是这个：

可能只是将补码指定为一种编码方式吧，所以正整数不能求补码，因为它的补码就是它的二进制表示？？

算了，反正我给出的分析中，”补码”指的是更广义的，正整数也能求补码（参见上图Three-bit signed integers），求补码的方式就是除符号位外，各位取反，然后+1。然后通过这个方式目算可能有点困难，于是还有一种简单的方式可以用来目算（原理一样）：从最低位到第一个1之间不变，其他位按位取反。

我本意是通过这个角度来说明该条件下只有0x00000000与其补码按位或运算之后最高位是0，其他数都是1，然后可以通过这个来实现逻辑非的操作。如评论区朋友所指，这个数也就是0，可参考评论区。

写在最后：关于补码的定义，有考试的话就按课本上的来吧。感谢评论区朋友的“指正”。

------------------------------------------------------------------------------------------------------------------

2019-6-15更新
要期末考试啦，翻了下书，发现第8个函数divpwr2中的偏置值为2^n-1的证明就在教材中，教材是华章教育的《深入理解计算机系统》（原书第2版），证明部分在P64-P66。

------------------------------------------------------------------------------------------------------------------

2019-3-30更新
感谢TJC大佬指正，下列第14个函数float_i2f思路中我的表述“四舍五入”不当，应当修改成向偶数舍入，也就是向最接近的值舍入。
------------------------------------------------------------------------------------------------------------------

1、bitAnd

 *   bitAnd - x&y using only ~ and | 
 *   Example: bitAnd(6, 5) = 4
 *   Legal ops: ~ |
 *   Max ops: 8
 *   Rating: 1

用~（按位取反）和|（按位或）表示&（按位与），由德摩根律可受启发

int bitAnd(int x, int y) 
{
	return ~((~x)|(~y));
}

2、getByte

 *   getByte - Extract byte n from word x
 *   Bytes numbered from 0 (LSB) to 3 (MSB)
 *   Examples: getByte(0x12345678,1) = 0x56
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 6
 *   Rating: 2

取整型的第多少个字节。编号是从LSB（Least Significant Bit，最低有效位为0）到MSB（Most Significant Bit，最高有效位为3）。利用按位与&，1&X=X，0&X=0（X代表0或1）的特性，只要把要取的第n个字节移到最低位后和0xff按位与，第n个字节会保留，编号大于n的字节会被清零。因为1个字节是8位，因此取第n个字节时要先将其右移8*n位，8*n用位运算可表示为（n<<3）

int getByte(int x, int n)
{
	return (x>>(n<<3))&0xff;
}

3、logicalShift

 *   logicalShift - shift x to the right by n, using a logical shift
 *   Can assume that 0 <= n <= 31
 *   Examples: logicalShift(0x87654321,4) = 0x08765432
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 20
 *   Rating: 3 

进行逻辑右移。因为c语言里的>>运算符默认是算术右移（算术右移符号位补位，逻辑右移0补位），所以可以先进行算术右移，再将补位的符号位（可能是0或1）换成0，这个替换的过程可以利用第二个函数用的方法，采用掩码。
假设要逻辑右移n位，就需要将最高位的n位符号位全部替换成0，那么就可以利用左边n位为0，右边32-n位为1的掩码与算术右移n位后的原码按位与&，便可得到逻辑右移n位后的目标数。
怎样构造这个掩码呢，先将1左移（不管是算术左移还是逻辑左移，都是0补位）31位，按位取反后，再右移(n-1)位，由于这里规定不能用减法（n+(-1)也行），故先左移n位再右移1位，这样最低位会变成0所以需要将其变成1。以n为4为例：

int logicalShift(int x, int n) 
{
	int mask;
  	x>>=n;
        mask=(((~(1<<31))>>n)<<1)|1;
        return x&mask;
}

4、bitCount

 *   bitCount - returns count of number of 1's in word
 *   Examples: bitCount(5) = 2, bitCount(7) = 3
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 40
 *   Rating: 4

求一个数的二进制表示中1的位数。采用自底向上的方式进行求解，先求两位中1的个数、再求四位中1的个数……最后求三十二位中1的个数，同时也利用到了掩码。

下图（图片来源见参考资料第一条）以8位为例，利用移位操作与掩码、按位与自底向上求解。

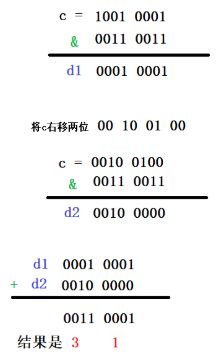
int bitCount(int x) 
{
        //若不能直接用这些数，可通过计算得到
  	int mask_1 =0x55555555;//01 01 01 01 01 01...
  	int mask_2 =0x33333333;//0011 0011 0011...
  	int mask_4 =0x0f0f0f0f;//00001111 00001111...
  	int mask_8 =0x00ff00ff;//0000000011111111 0000000011111111
  	int mask_16=0x0000ffff;//00000000000000001111111111111111
  	x=(x&mask_1)+((x>>1)&mask_1);
  	x=(x&mask_2)+((x>>2)&mask_2);
  	//下面三组最高位不会是1了 ，减少运算次数
  	x=(x+(x>>4))&mask_4;//x=(x&mask_4)+((x>>4)&mask_4);
  	x=(x+(x>>8))&mask_8;//x=(x&mask_8)+((x>>8)&mask_8);
  	x=(x+(x>>16))&mask_16;//x=(x&mask_16)+((x>>16)&mask_16);
  	return x;
}

修改如下：
 

int bitCount(int x) 
{
  	int mask_1,mask_2,mask_4,mask_8,mask_16;
  	mask_1=0x55|(0x55<<8);
  	mask_1=mask_1|(mask_1<<16);
  	mask_2=0x33|(0x33<<8);
  	mask_2=mask_2|(mask_2<<16);
  	mask_4=0x0f|(0x0f<<8);
  	mask_4=mask_4|(mask_4<<16);
  	mask_8=0xff|(0xff<<16);
  	mask_16=0xff|(0xff<<8);
  	x=(x&mask_1)+((x>>1)&mask_1);
  	x=(x&mask_2)+((x>>2)&mask_2);
  	//下面三组最高位不会是1了 
  	x=(x+(x>>4))&mask_4;//x=(x&mask_4)+((x>>4)&mask_4);
  	x=(x+(x>>8))&mask_8;//x=(x&mask_8)+((x>>8)&mask_8);
  	x=(x+(x>>16))&mask_16;//x=(x&mask_16)+((x>>16)&mask_16);
  	return x;
}

5、bang

 *   bang - Compute !x without using !
 *   Examples: bang(3) = 0, bang(0) = 1
 *   Legal ops: ~ & ^ | + << >>
 *   Max ops: 12
 *   Rating: 4 

不利用逻辑符号!求一个数的逻辑非，也就是判断该数的二进制位是否全为0，若全为0则返回1，否则返回0。
我们知道一个求补码的方法：从最低位到第一个1之间不变，其他位按位取反。
以八位为例，如10010010的补码为01101110，10000000的补码为10000000，00000000的补码为00000000。
可以得出，32位中只有0x00000000和0x80000000的补码是其本身，且只有0x00000000与其补码按位或运算之后最高位是0，其他数都是1。将原码与其补码按位或后右移31位判断最高位，若最高位为0说明原码是0应该返回1，若最高位是1说明原码不是0返回0。

int bang(int x) 
{
    int mask=~x+1;//x的补码
    return ~((x|mask)>>31)&1; //移位后进行位反操作再&1，得到正确映射关系
}

6、tmin

 *   tmin - return minimum two's complement integer 
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 4
 *   Rating: 1

返回最小的二进制补码integer。1000 0000 0000 0000 0000 0000 0000 0000即0x80000000

int tmin(void)
{
  	return 0x80<<24;
}

7、fitsBits

 *  fitsBits - return 1 if x can be represented as an 
 *  n-bit, two's complement integer.
 *   1 <= n <= 32
 *   Examples: fitsBits(5,3) = 0, fitsBits(-4,3) = 1
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 15
 *   Rating: 2

判断x能否由n位二进制补码表示。x是肯定能用32位表示的，能否用n位表示可看成符号拓展的逆过程。所以经过x<<(32-n)>>(32-n)后若与原来的x相等则表示能用n位二进制补码表示x。判断相等可利用异或，相同为0，不同为1，前面加个!得到正确映射关系。

 

int fitsBits(int x, int n) 
{
	int shiftnumber=32+~n+1;//32-n
        int xx=x<>shiftnumber;
        return !(xx^x);//和原来相同返回1，表示能用n位表示 
}

8、divpwr2

 *  divpwr2 - Compute x/(2^n), for 0 <= n <= 30
 *  Round toward zero
 *   Examples: divpwr2(15,1) = 7, divpwr2(-33,4) = -2
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 15
 *   Rating: 2

将一个数x除以2的n次方。若x代表正数，直接右移n位即可，即x/(2^n)=x>>n。若x代表负数，除法与右移并不相同，原因是除法是向0取整，而右移位是向负取整（见参考资料第3条），此时x/(2^n)=(x+(1<>n。（由于不能用-号，-1可用~0表示，此处偏置值为何是2^n-1呢，卡了好久，没找出证明就先记着吧）。接下来需要构造一个数使得其在x为正数时等于0，x为负数时等于(1<

int divpwr2(int x, int n) 
{
    int mask=x>>31;
    int bias=mask&((1<>n;
}

9、negate

 *   negate - return -x 
 *   Example: negate(1) = -1.
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 5
 *   Rating: 2

求相反数。送分题。先按位取反再加个1。

int negate(int x) 
{
  	return ~x+1;
}

10、isPositive

 *  isPositive - return 1 if x > 0, return 0 otherwise 
 *   Example: isPositive(-1) = 0.
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 8
 *   Rating: 3

判断是否大于0。正数的符号位为0，0的符号位也为0。

int isPositive(int x) 
{
  	return !((!x)|(x>>31));
}

11、isLessOrEqual

 *  isLessOrEqual - if x <= y  then return 1, else return 0 
 *   Example: isLessOrEqual(4,5) = 1.
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 24
 *   Rating: 3

若y>=x则返回1。将y-x（y+~x+1），当y、x同号时判断y-x符号位即可，当y、x异号时可能会发生溢出，需要看y、x的符号位。

int isLessOrEqual(int x, int y) 
{
  	int signx=(x>>31)&1;//x的符号位 
  	int signy=(y>>31)&1;//y的符号位 
  	int signy_x=((y+~x+1)>>31)&1;//y-x的符号位 
  	return (!(signx^signy)&!signy_x) | ((signx^signy)&signx);//同号 异号 
}

12、ilog2

 *  ilog2 - return floor(log base 2 of x), where x > 0
 *   Example: ilog2(16) = 4
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 90
 *   Rating: 4

返回log(x)。即求最高位1的索引（0~31）。详见注释。

int ilog2(int x) 
{
	int sign,shift1,shift2,shift3,shift4,shift5;
  	sign=!!(x>>16);//若x表示的二进制数左边16位没有1，sign为0,有1则sign为1 
  	shift1=sign<<4;//0^4 or 2^4
	x=x>>shift1;//若sign为1，丢掉右边16位，因为1必定出现在左边16位中 
	
	sign=!!(x>>8);//若x表示的二进制数左边8位没有1，sign为0,有1则sign为1 
	shift2=sign<<3;//0^3 or 2^3
	x=x>>shift2;//若sign为1，丢掉右边8位，因为1必定出现在左边8位中 
	
	sign=!!(x>>4);//若x表示的二进制数左边4位没有1，sign为0,有1则sign为1 
	shift3=sign<<2;//0^2 or 2^2
	x=x>>shift3;//若sign为1，丢掉右边4位，因为1必定出现在左边4位中 
	
	sign=!!(x>>2);//若x表示的二进制数左边2位没有1，sign为0,有1则sign为1 
	shift4=sign<<1;//0^1 or 2^1
	x=x>>shift4;//若sign为1，丢掉右边2位，因为1必定出现在左边2位中 
	
	sign=!!(x>>1);//若x表示的二进制数左边1位没有1，sign为0,有1则sign为1 
	shift5=sign; 
	
	return shift1+shift2+shift3+shift4+shift5;//偏移量相加即得结果 
}

13、float_neg

 *  float_neg - Return bit-level equivalent of expression -f for
 *   floating point argument f.
 *   Both the argument and result are passed as unsigned int's, but
 *   they are to be interpreted as the bit-level representations of
 *   single-precision floating point values.
 *   When argument is NaN, return argument.
 *   Legal ops: Any integer/unsigned operations incl. ||, &&. also if, while
 *   Max ops: 10
 *   Rating: 2

当实参为NaN时（阶码全为1，小数域非零），返回该实参。其他情况更改一下符号位即可。
阶码为第23位到第30位共8位，小数域为第0位到第22位共23位。
判断阶码是否全为1：(uf>>23)&0xff^0xff，若全为1则结果为0x00
判断小数域是否全为0：!(uf&((1<<23)-1)，若全为0则结果为1，否则为0
更改符号位（最高位）：uf^(1<<31)

unsigned float_neg(unsigned uf) 
{
  	if((((uf>>23)&0xff)^0xff)||!(uf&((1<<23)-1))) uf=(1<<31)^uf;
  	return uf;
}

14、float_i2f

 *   float_i2f - Return bit-level equivalent of expression (float) x
 *   Result is returned as unsigned int, but
 *   it is to be interpreted as the bit-level representation of a
 *   single-precision floating point values.
 *   Legal ops: Any integer/unsigned operations incl. ||, &&. also if, while
 *   Max ops: 30
 *   Rating: 4

将int型转换为float型。
符号位（sign）：看最高有效位即可；
int型（二进制表示）可假想小数点在最低有效位右边，（所以肯定是左移了），左移shiftnum-1位，使得小数点移动到第一个有效数字（1）的右边（不代表小数点移动的是shiftnum-1位，这里利用左移使得第一个有效数字1在最高有效位，可以计算小数点移动了32-shiftnum位），那么小数点右边第1位（首位）到第23位就是浮点数表示的尾数部分了，因为这里只要取23位所以存在精度问题，这里采取四舍五入向偶数舍入的方式；
阶码部分看小数点移动的位数，加上偏置置（float中为127）即可。即(127+32-shiftnum)<<23。

unsigned float_i2f(int x) 
{
	//注意这里定义的是unsigned，右移和左移都会是逻辑移位，即补0 
	unsigned absx,sign,flag,temp,aftershift,shiftnum;
	absx=x;
	sign=x&(1<<31);//符号位
	if(sign) absx=-x;
	aftershift=absx; 
	if(!x) return 0; 
	shiftnum=0;
	//左移shiftnum-1位 
	while(1)
	{
		temp=aftershift;
		//aftershift要多移一位，aftershift的高位往低位数共23位即float的尾码部分 
		aftershift=aftershift<<1;
		shiftnum++;
		if(temp&0x80000000) break;//1000 0000 0000…… ，最高位为1 
	}
	//aftershift的前23位要充当float的尾码部分，四舍五入，判断进位 
  	if((aftershift&0x01ff)>0x0100)  flag=1;//后9位中 第1位为1，后8位有1 
	else if((aftershift&0x03ff)==0x0300) flag=1;//后9位中 第一位为1，后8位为0
	else flag=0;
	return  sign+((159-shiftnum)<<23)+(aftershift>>9)+flag;
}

15、float_twice

 *   float_twice - Return bit-level equivalent of expression 2*f for
 *   floating point argument f.
 *   Both the argument and result are passed as unsigned int's, but
 *   they are to be interpreted as the bit-level representation of
 *   single-precision floating point values.
 *   When argument is NaN, return argument
 *   Legal ops: Any integer/unsigned operations incl. ||, &&. also if, while
 *   Max ops: 30
 *   Rating: 4
计算float类型的uf的两倍。
可以看到，对于非规格化值使阶码值为1-Bias而不是简单的-Bias提供了一种从非规格化值平滑转换到规格化值的方法。

unsigned float_twice(unsigned uf) 
{
	if((uf&0x7f800000)==0)  //阶码为0，非规格化数
		uf=((uf&0x007fffff)<<1)|(uf&0x80000000);//尾数域左移一位，别忘了符号
	else if((uf&0x7f800000)!=0x7f800000) //不是NaN ，阶码不是全1 
		uf=uf+0x800000;//阶码+1，2^(1+1)=2*2 
	//NaN，就地返回吧 
  	return uf;
}

 

检测结果：

参考资料：
1、https://www.52pojie.cn/thread-789291-1-1.html
2、https://blog.csdn.net/qq_19762007/article/details/80038755
3、https://www.cnblogs.com/tlz888/p/9185403.html
4、https://blog.csdn.net/u014124795/article/details/38471797
5、https://blog.csdn.net/lwfcgz/article/details/8515188