15 离群点和高杠杆率点
15 离群点和高杠杆率点
标签:机器学习与数据挖掘
(此篇R代码对应本博客系列《12 R语言手册(第五站 多元回归》)
1.离群值
离群值的标准残差的据绝对值非常大,我们研究的时候可以单独把这类值来出来看一下,以使我们的预测模型的不会受到太大干扰。
那我们如何揪出离群值呢?看图
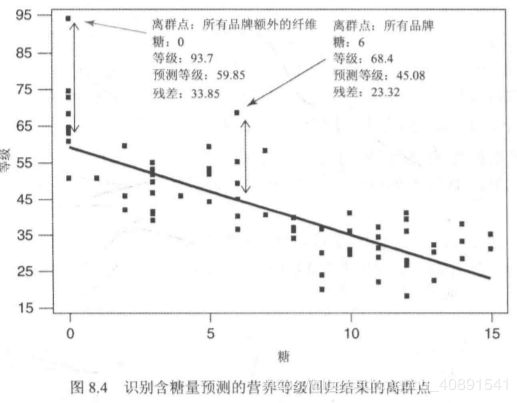
这里有两个特别离群的点,他们的残差都比一般的值要大一些。但是对于不同的变量,就有不同的度量和方差,我们需要将它们标准化,这样就有了标准残差。
令 S i , resid S_{i, \text {resid}} Si,resid表示第 i i i 个残差的标准误差 ,则:
s i , resid = s 1 − h i s_{i, \text {resid}}=s \sqrt{1-h_{i}} si,resid=s1−hi
(其中, h i h_i hi表示第i个观察对象的杠杆率点。)
标准残差 等于:
residual i , standardized = y i − y ^ i s i , resid _{i, \text { standardized }}=\frac{y_{i}-\hat{y}_{i}}{s_{i, \text {resid}}} i, standardized =si,residyi−y^i
以经验之谈的话,标准残差值超过2的话,就视为离群点。
2.高杠杆率点
话说回来,在定义残差的标准误差时,没有给出高杠杆率点的定义,现在给出。第 i i i 个观察点的杠杆率点 h i h_i hi 定义如下:
h i = 1 n + ( x i − x ‾ ) 2 ∑ ( x i − x ‾ ) 2 h_{i}=\frac{1}{n}+\frac{\left(x_{i}-\overline{x}\right)^{2}}{\sum\left(x_{i}-\overline{x}\right)^{2}} hi=n1+∑(xi−x)2(xi−x)2
给定数据集,其中 1 / n 1/n 1/n和 ∑ ( x i − x ‾ ) 2 \sum\left(x_{i}-\overline{x}\right)^{2} ∑(xi−x)2可以认为是常量,因此第;个观察点的杠杆率点仅依赖 ( x i − x ‾ ) 2 \left(x_{i}-\overline{x}\right)^{2} (xi−x)2,即预测变量值与预测变量均值的差的平方。在x取值范围内,观察点与观察点均值的差别越大,杠杆率值就越大。杠杆率点最低取值为 1 / n 1/n 1/n,最大取值为 1。观察点的杠杆率值比 2 ( m + 1 ) / n 2(m+1)/n 2(m+1)/n或 3 ( m + 1 ) / n 3(m+1)/n 3(m+1)/n大,则可以认为其杠杆率值较高(其中m表示预测变量的个数)。
比如,在定向旅行中,假设具有一个新的观察点,一个实际的优秀定向运动竞争,他运动了16小时,运动距离为39千米。图8.5给出了散点图,更新为11个参与者。
这就说明这是一个高杠杆率点吗?是的。我们先来看这11个数据的回归分析结果:
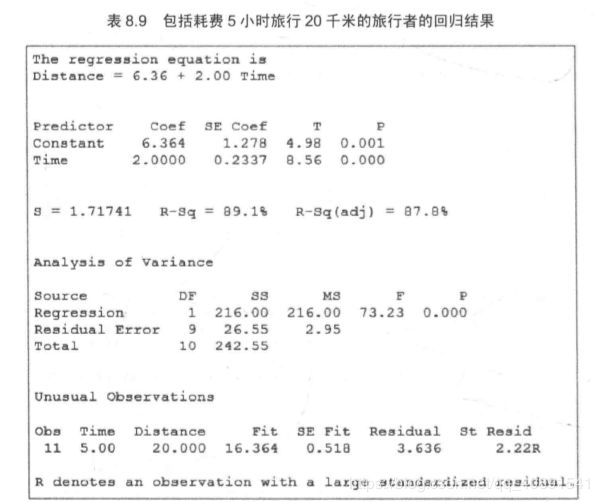
现在,我们考察该观察者是否具有影响。评估新观察点出现后对回归系数的影响情况。y轴截距发生了变化,从 b 0 b_0 b0=6.00变化为 b 0 b_0 b0=6.36。但新旅行者的出现并未使斜率发生变化,仍然是 b 1 b_1 b1=2.00。
这个离群点对估计回归有一定的影响力,稍稍使截距移动了一点,但是未对斜率造成影响。
我们再说说这个杠杆率的取名含义,如果一个点,加入之后,可以使一个线性模型变动特别大,那么它就是高杠杆率点。虽然这里它没有使模型发生很大的变化。
3.例子
这个时候,我们就应该再捋一捋概念,算一算题目了。
观察如下数据集:
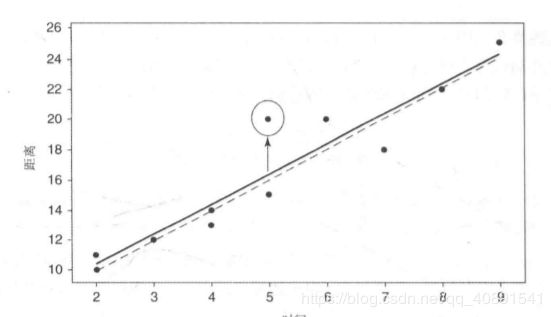
可如下计算该观察点的杠杆率(x=5,y=20)。由 x ^ \hat{x} x^=5,可得:
∑ ( x i − x ‾ ) 2 = ( 2 − 5 ) 2 + ( 2 − 5 ) 2 + ( 3 − 5 ) 2 + … + ( 9 − 5 ) 2 + ( 5 − 5 ) 2 = 54 \sum\left(x_{i}-\overline{x}\right)^{2}=(2-5)^{2}+(2-5)^{2}+(3-5)^{2}+\ldots+(9-5)^{2}+(5-5)^{2}=54 ∑(xi−x)2=(2−5)2+(2−5)2+(3−5)2+…+(9−5)2+(5−5)2=54
由此可得该新观察点的杠杆率为:
h ( s , 20 ) = 1 11 + ( 5 − 5 ) 2 54 = 0.0909 h_{(s, 20)}=\frac{1}{11}+\frac{(5-5)^{2}}{54}=0.0909 h(s,20)=111+54(5−5)2=0.0909
在得到该观察点的杠杆率后,我们可以如下得到标准残差。首先,获得残差的标准误差:
s ( 5 , 20 ) , r a i d = 1.71741 1 − 0.0909 = 1.6375 s_{(5,20), \mathrm{raid}}=1.71741 \sqrt{1-0.0909}=1.6375 s(5,20),raid=1.717411−0.0909=1.6375
由此获得标准残差:
r e s i d u a l ( 5 , 20 ) , standardized = y i − y ^ i s ( 5 , 20 ) , resid = 20 − 16.364 1.6375 = 2.22 residual_{(5,20), \text { standardized }}=\frac{y_{i}-\hat{y}_{i}}{s_{(5,20), \text { resid }}}=\frac{20-16.364}{1.6375}=2.22 residual(5,20), standardized =s(5,20), resid yi−y^i=1.637520−16.364=2.22
注意它的标准残差值是2.22,比2.0稍大一定,因此,它被视为轻度离群点。
4.库克距离
库克距离是最常用的度量观察点影响的方法。它既考虑到观察点残差的大小,又考虑了杠杆率。对第i个观察点,库克距离形式如下:
D i = ( y i − y ^ i ) 2 ( m + 1 ) s 2 [ h i ( 1 − h i ) 2 ] D_{i}=\frac{\left(y_{i}-\hat{y}_{i}\right)^{2}}{(m+1) s^{2}}\left[\frac{h_{i}}{\left(1-h_{i}\right)^{2}}\right] Di=(m+1)s2(yi−y^i)2[(1−hi)2hi]
(其中 ( y i − y ^ i ) \left(y_{i}-\hat{y}_{i}\right) (yi−y^i)表示第 $ i $ 个观察点的残差, s s s 表示估计的标准差, h i h_i hi 表示第 $ i $ 个观察点的杠杆率,$ m $ 表示预测变量的数目。)
确定某一观察点是否具有影响的经验规则是其库克距离超过1.0。更精确地说,也可以比较库克距离与具有(m,n-m-1)自由度的 F F F 分布的百分位数。如果观察值位于该分布的第1个四分之一位(低于25%),则观察点对回归的影响较小。如果库克距离大于该分布的中位数,则该观察点具有一定的影响。对上述观察点来说,其库克距离为0.2465,位于 F 2 , 9 F_{2,9} F2,9 分布的第22个百分位处,表明该观察点的影响较小。