图像旋转算法原理 Python实现
旋转原理
参考博客:https://blog.csdn.net/liyuan02/article/details/6750828
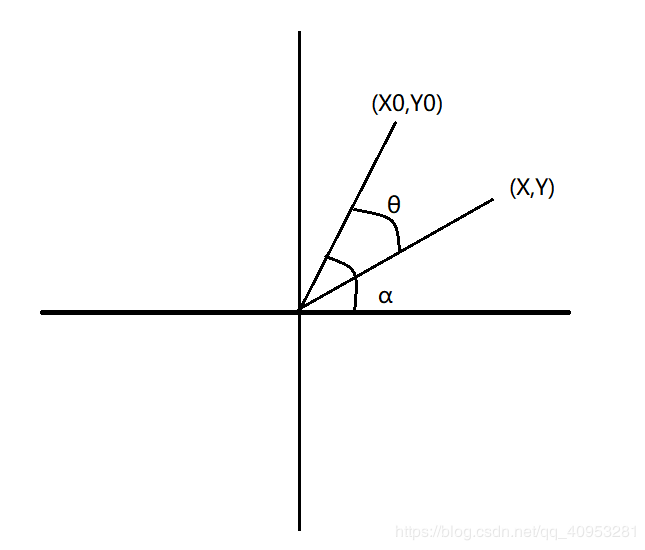
如下图,推导点 ( x 0 , y 0 ) (x_0,y_0) (x0,y0)旋转 θ \theta θ到到点 ( x , y ) (x,y) (x,y),半径为R
对于两点坐标可以这样表示:
x 0 = R ∗ cos α y 0 = R ∗ sin α F o r : x x = R ∗ cos ( α − θ ) = R ∗ ( cos α cos θ + sin α sin θ ) = x 0 cos θ + y 0 sin θ F o r : y y = R ∗ ( sin ( α − θ ) ) = R ∗ ( sin α cos θ − cos α sin θ ) = y 0 cos θ − x 0 sin θ \begin{aligned} x_0 =& R*\cos\alpha \\ y_0 =& R*\sin\alpha \\ For:x\\ x =& R*\cos(\alpha-\theta) \\ =& R*(\cos\alpha\cos\theta+\sin\alpha\sin\theta) \\ =& x_0\cos\theta+y_0\sin\theta \\ For:y\\ y =& R*(\sin(\alpha-\theta)) \\ =& R*(\sin\alpha\cos\theta-\cos\alpha\sin\theta) \\ =& y_0\cos\theta-x_0\sin\theta \end{aligned} x0=y0=For:xx===For:yy===R∗cosαR∗sinαR∗cos(α−θ)R∗(cosαcosθ+sinαsinθ)x0cosθ+y0sinθR∗(sin(α−θ))R∗(sinαcosθ−cosαsinθ)y0cosθ−x0sinθ
使用矩阵表示有:
[ x y 1 ] = [ x 0 y 0 1 ] ∗ [ cos θ − sin θ 0 sin θ cos θ 0 0 0 1 ] \left[ \begin{matrix} x & y & 1 \end{matrix} \right]= \left[ \begin{matrix} x_0 & y_0 & 1 \end{matrix} \right] * \left[ \begin{matrix} \cos\theta & -\sin\theta & 0 \\ \sin\theta & \cos\theta & 0 \\ 0 & 0 & 1 \end{matrix} \right] [xy1]=[x0y01]∗⎣⎡cosθsinθ0−sinθcosθ0001⎦⎤
此为顺时针旋转 θ \theta θ ,逆时针旋转 θ \theta θ只需要将 θ = − θ \theta=-\theta θ=−θ 即可,易得: ( x , y ) → ( x 0 , y 0 ) (x,y)\rightarrow(x_0,y_0) (x,y)→(x0,y0)
[ x 0 y 0 1 ] = [ x y 1 ] ∗ [ cos θ sin θ 0 − sin θ cos θ 0 0 0 1 ] \left[ \begin{matrix} x_0 & y_0 & 1 \end{matrix} \right]= \left[ \begin{matrix} x & y & 1 \end{matrix} \right]* \left[ \begin{matrix} \cos\theta & \sin\theta & 0 \\ -\sin\theta & \cos\theta & 0 \\ 0 & 0 & 1 \end{matrix} \right] [x0y01]=[xy1]∗⎣⎡cosθ−sinθ0sinθcosθ0001⎦⎤
用于实际的旋转矩阵
上一部分的旋转矩阵是以数字坐标系推导的,而图像坐标系是以左上角为原点的图像坐标系,我们需要将图像坐标系转换为数字坐标系,方便的也需要从数字坐标系到图像坐标系的逆转换
假设原图片大小为 W , H W,H W,H,旋转后所包含图片的最小矩形大小为 W ′ , H ′ W^{'},H^{'} W′,H′
设数字坐标系点为 ( x , y ) (x,y) (x,y)其相应的图像坐标系点为 ( x 0 , y 0 ) (x_0,y_0) (x0,y0) 有如下表达式:
[ x y 1 ] = [ x 0 y 0 1 ] ∗ [ 1 0 0 0 − 1 0 − 0.5 W 0.5 H 1 ] [ x 0 y 0 1 ] = [ x y 1 ] ∗ [ 1 0 0 0 − 1 0 0.5 W ′ 0.5 H ′ 1 ] \left[ \begin{matrix} x & y & 1 \end{matrix} \right] = \left[ \begin{matrix} x_0 & y_0 & 1 \end{matrix} \right] * \left[ \begin{matrix} 1 & 0 & 0 \\ 0 & -1 & 0 \\ -0.5W & 0.5H & 1 \end{matrix} \right] \left[ \begin{matrix} x_0 & y_0 & 1 \end{matrix} \right] = \left[ \begin{matrix} x & y & 1 \end{matrix} \right]* \left[ \begin{matrix} 1 & 0 & 0 \\ 0 & -1 & 0 \\ 0.5W^{'} & 0.5H^{'} & 1 \end{matrix} \right] [xy1]=[x0y01]∗⎣⎡10−0.5W0−10.5H001⎦⎤[x0y01]=[xy1]∗⎣⎡100.5W′0−10.5H′001⎦⎤
假设在图像坐标系中有点 ( x 0 , y 0 ) (x_0,y_0) (x0,y0)顺时针旋转 θ \theta θ 到 ( x , y ) (x,y) (x,y)处转换后大小为 W ′ , H ′ W^{'},H^{'} W′,H′,转换公式有:
(1) [ x y 1 ] = [ x 0 y 0 1 ] ∗ [ 1 0 0 0 − 1 0 − 0.5 W 0.5 H 0 ] ∗ [ cos θ − sin θ 0 sin θ cos θ 0 0 0 1 ] ∗ [ 1 0 0 0 − 1 0 0.5 W ′ 0.5 H ′ 1 ] \left[ \begin{matrix} x & y & 1 \end{matrix} \right]= \left[ \begin{matrix} x_0 & y_0 & 1 \end{matrix} \right] * \left[ \begin{matrix} 1 & 0 & 0 \\ 0 & -1 &0 \\ -0.5W & 0.5H & 0 \\ \end{matrix} \right] * \left[ \begin{matrix} \cos\theta & -\sin\theta & 0 \\ \sin\theta & \cos\theta & 0 \\ 0 & 0 & 1 \end{matrix} \right] * \left[ \begin{matrix} 1 & 0 & 0 \\ 0 & -1 & 0 \\ 0.5W^{'} & 0.5H^{'} & 1 \end{matrix} \right]\tag{1} [xy1]=[x0y01]∗⎣⎡10−0.5W0−10.5H000⎦⎤∗⎣⎡cosθsinθ0−sinθcosθ0001⎦⎤∗⎣⎡100.5W′0−10.5H′001⎦⎤(1)
(2) [ x 0 y 0 1 ] = [ x y 1 ] ∗ [ 1 0 0 0 − 1 0 − 0.5 W ′ 0.5 H ′ 1 ] ∗ [ cos θ sin θ 0 − sin θ cos θ 0 0 0 1 ] ∗ [ 1 0 0 0 − 1 0 0.5 W 0.5 H 0 ] \left[ \begin{matrix} x_0 & y_0 & 1 \end{matrix} \right]= \left[ \begin{matrix} x & y & 1 \end{matrix} \right] * \left[ \begin{matrix} 1 & 0 & 0 \\ 0 & -1 & 0 \\ -0.5W^{'} & 0.5H^{'} & 1 \end{matrix} \right] * \left[ \begin{matrix} \cos\theta & \sin\theta & 0 \\ -\sin\theta & \cos\theta & 0 \\ 0 & 0 & 1 \end{matrix} \right] * \left[ \begin{matrix} 1 & 0 & 0 \\ 0 & -1 &0 \\ 0.5W & 0.5H & 0 \\ \end{matrix} \right]\tag{2} [x0y01]=[xy1]∗⎣⎡10−0.5W′0−10.5H′001⎦⎤∗⎣⎡cosθ−sinθ0sinθcosθ0001⎦⎤∗⎣⎡100.5W0−10.5H000⎦⎤(2)
(1)式为前向映射(直接从原图映射到旋转后的图),(2)式为后向映射(用于旋转后映射到旋转前)
为什么需要后向映射而不是前向映射
之所以有后向映射是因为在前向映射中获取的旋转后坐标是浮点数,但是像素只能是整数,所以就产生了像素缺失
而从后向前映射像素信息都是存在的,但又存在映射到原图中的浮点坐标改如何选择颜色信息的问题
这就有内插值的问题,提供的解决办法有三个,最邻近内插、双线性内插、双三次内插,最邻近就是直接对浮点坐标取整,取最接近它的像素值,双线性内插就是取与它相邻的4个点,求线性渲染值
其本质就是:假设在数轴上有两个点A,B(A 双三次内插有点麻烦,这里。。我也不清楚,嘿嘿 可以参考https://blog.csdn.net/caomin1hao/article/details/81092134 所需外部库: 使用按像素遍历,比较耗时 后向映射中使用最邻近内插和双线性内插(双三次内插暂未处理) 可以看出来双线性比最邻近好的多了Python 实践
import numpy as np
import matplotlib.pyplot as plt
import skimage.data
import skimage.io
angle = 30*np.pi/180
# 读取库图片 Attention 转换 默认为int8 运算时可能会溢出
img = skimage.data.chelsea().astype(int)
# 设置新的图像大小
h,w = img.shape[0],img.shape[1]
newW = int(w*abs(np.cos(angle)) + h*abs(np.sin(angle)))+1
newH = int(w*abs(np.sin(angle)) + h*abs(np.cos(angle)))+1
# Attention dtype
newimg1 = np.zeros((newH,newW,3),dtype = int)
newimg2 = np.zeros((newH,newW,3),dtype = int)
newimg3 = np.zeros((newH,newW,3),dtype = int)
# 设置旋转矩阵 scr -> dex
trans1 = np.array([[1,0,0],[0,-1,0],[-0.5*w,0.5*h,1]])
trans1 = trans1.dot(np.array([[np.cos(angle),-np.sin(angle),0],[np.sin(angle),np.cos(angle),0],[0,0,1]]))
trans1 = trans1.dot(np.array([[1,0,0],[0,-1,0],[0.5*newW,0.5*newH,1]]))
# des -> src
trans2 = np.array([[1,0,0],[0,-1,0],[-0.5*newW,0.5*newH,1]])
trans2 = trans2.dot(np.array([[np.cos(angle),np.sin(angle),0],[-np.sin(angle),np.cos(angle),0],[0,0,1]]))
trans2 = trans2.dot(np.array([[1,0,0],[0,-1,0],[0.5*w,0.5*h,1]]))
# 开始旋转
for x in range(w):
for y in range(h):
newPos = np.array([x,y,1]).dot(trans1)
newimg1[int(newPos[1])][int(newPos[0])] = img[y][x]
for x in range(newW):
for y in range(newH):
srcPos = np.array([x,y,1]).dot(trans2)
if srcPos[0] >= 0 and srcPos[0] < w and srcPos[1] >= 0 and srcPos[1] < h:
# 最邻近内插
newimg2[y][x] = img[int(srcPos[1])][int(srcPos[0])]
# 双线性内插
bix,biy = int(srcPos[0]),int(srcPos[1]) # 取左上角坐标
# 避免最后一行溢出
if bix < w-1 and biy < h-1:
# 沿 X 方向线性内插
rgbX1 = img[biy][bix] + (img[biy][bix+1] - img[biy][bix])*(srcPos[0]-bix)
rgbX2 = img[biy+1][bix] + (img[biy+1][bix+1] - img[biy+1][bix])*(srcPos[0]-bix)
# 沿 Y 方向内插
rgb = rgbX1 + (rgbX2-rgbX1)*(srcPos[1]-biy)
newimg3[y][x] = rgb
# 绘图
sub = plt.subplot(2,2,1)
sub.set_title("Src Img")
plt.imshow(img)
sub = plt.subplot(2,2,2)
sub.set_title("Src->Des")
plt.imshow(newimg1)
sub = plt.subplot(2,2,3)
sub.set_title("Des->Src & Nearest")
plt.imshow(newimg2)
sub = plt.subplot(2,2,4)
sub.set_title("Des->Src & Bilinear")
plt.imshow(newimg3)
plt.show()
效果图展示