数据结构绪论（1）

之后写的一些数据结构的内容和感想是基于清华大学的数据结构（C++语言版   第3版）以及对应的网课，后续会在PTA上面刷浙大的数据结构题目集，会挑一部分有趣的题目贴过来，记一下解题思路。希望能好好学好数据结构，加油咯！

目录

第一章      绪论(1)

1.1计算机与算法

1.绳索计算机

2.尺规计算机

3.冒泡排序（起泡排序）

4.算法 ：

5.什么是好算法 :

---

第一章      绪论(1)

1.1计算机与算法

在开篇作者就说，人与动物的根本区别是在于理性，而计算是理性的重要而具体的形式。计算机是人类从事计算的工具，是抽象计算模型的具体物化。让我想起了高中语文老师对人的定义--一种能制造并且会使用工具的高等动物，之所以有区别是我们能制造出类似计算机这样的工具，并且能去不断发展使用好它。要想去驾驭好计算机，我们得通过深入思考与分析获得对问题本质的透彻理解，按照积淀的框架与模式设计设计出合乎问题内在规律的算法，选用、改进或定制足以支撑算法高效实现的数据结构。

计算机科学（computer science）的核心在于研究计算方法与过程的规律，而不仅仅是作为计算工具的计算机本身，因此E. Dijkstra及其追随者更倾向于将这门科学称作计算科学（computing science）。

计算 = 信息处理

计算模型 = 计算机 = 信息处理工具

1. 计算机的本质是计算，计算是寻找对象的规律，并从中找到技巧。计算的目标是高效，低耗。

2. 算法就是借助一定的工具，在一定的规则下，以明确而机械的形式来进行的计算。
算法定义：基于特定的计算类型，旨在解决某一信息处理问题而设计的一个指令序列。

首先给出了三个例子，来说计算机与算法的关系

1.1.1绳索计算机

作者用这个例子说明这套计算工具与计算机在本质来看，它们的相似之处多余差异之处，都是用于支持和实现计算过程的物理机制。

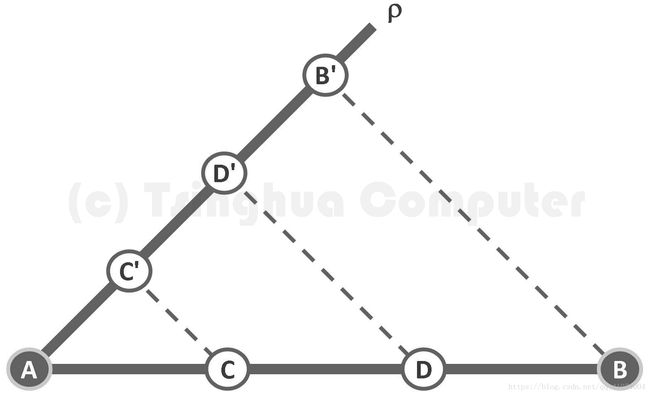
1.1.2.尺规计算机

第二个例子是在AB上取出等分点，用直尺和圆规构成的一种物理机制类比来看计算机。

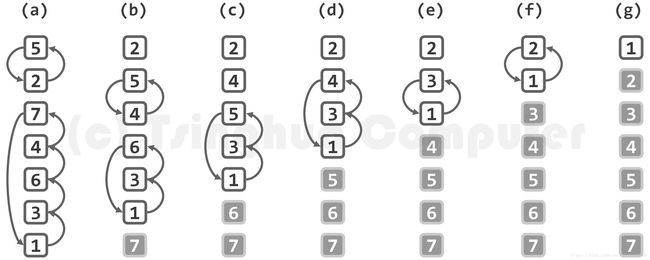
1.1.3.冒泡排序（起泡排序）

这是正式的在讲第一个算法，用于排序的冒泡排序（从一开始学C老师就是这样叫的，所以觉得书上的起泡排序不是很习惯）

乍一看觉得这个排序有点复杂，但是很好理解，每次循环的时候将前后两个元素排序，从头到尾，不断将顺序拍好的元素往后排，使得它从局部有序慢慢变成整体有序，像气泡在水中的上下浮动，大的气泡慢慢浮出水面。在CS50的一集末尾有请学生在台上演示，感觉很形象。https://www.bilibili.com/video/av26393783/?p=8

代码如下 ：

0001    void bubblesort1A ( int A[], int n ) { //起泡排序算法（版本1A）：0 <= n
0002      bool sorted = false; //整体排序标志，首先假定尚未排序
0003        while ( !sorted ) { //在尚未确认已全局排序之前，逐趟进行扫描交换
0004          sorted = true; //假定已经排序
0005          for ( int i = 1; i < n; i++ ) { //自左向右逐对检查当前范围A[0, n)内的各相邻元素
0006            if ( A[i - 1] > A[i] ) { //一旦A[i - 1]与A[i]逆序，则
0007              swap ( A[i - 1], A[i] ); //交换之，并
0008              sorted = false; //因整体排序不能保证，需要清除排序标志
0009            }
0010         }
0011         n--; //至此末元素必然就位，故可以缩短待排序序列的有效长度
0012      }
0013    } //借助布尔型标志位sorted，可及时提前退出，而不致总是蛮力地做n - 1趟扫描交换
 

1.1.4.算法 ：

1. 一个有限制令集
2. 接受一些输入(有些情况不需要输入)
3. 产生输出
4. 一定在有限步骤之后终止

• 有充分明确的目标,不可以有歧义
• 计算机能处理的范围之内
• 描述应不依赖于任何一种计算机语言以及具体的实现手段

 

算法应该具有以下几点 :

1. 输入与输出
2. 基本操作、确定性与可行性
3. 有穷性与正确性
4. 退化与鲁棒性
5. 重用性

1.输入与输出

输入 ：对所求解决问题特定实例的这种描述

输出 ：经过计算与处理之后得到的信息，即针对输入问题实例的答案

2.基本操作、确定性与可行性

基本操作 ：若干语义明确的指令序列

确定性与可行性 ：算法应可描述为由若干语义明确的基本操作组成的指令序列，且每一基本操作在对应的计算模型中均可兑现。

3.有穷性与正确性

有穷性 ：算法应在执行有限次基本操作之后终止并给出输出

正确性 ：所给的输出应符合由问题本身在事先确定的的条件

4.退化与鲁棒性

退化与鲁棒性 ：如算法数据的各种极端的输入实例都属于退化(degeneracy)情况，鲁棒性(robustness)要求尽可能充分地应对此类情况。  鲁棒性-->健壮性

1.1.5.什么是好算法 :

在视频中老师首先从三个问题引入了计算问题。接着又说明了什么是算法，算法的特点有哪些，这些特点中什么又是最关键的。算法分析包括了正确性的分析以及效率界定.通过求hailstone序列长度的例子说明了 程序≠算法。 本门课的重点在算法的效率上。 (算法+数据结构)*效率=解决问题