Leetcode动态规划算法题(Java实现)
算法很差,最近准备刷算法题,先从动态规划开始。
含义
动态规划(Dynamic programming,简称 DP)是一种在数学、管理科学、计算机科学、经济学和生物信息学中使用的,通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。
动态规划常常适用于有重叠子问题和最优子结构性质的问题,动态规划方法所耗时间往往远少于朴素解法。
动态规划背后的基本思想非常简单。大致上,若要解一个给定问题,我们需要解其不同部分(即子问题),再根据子问题的解以得出原问题的解。动态规划往往用于优化递归问题,例如斐波那契数列,如果运用递归的方式来求解会重复计算很多相同的子问题,利用动态规划的思想可以减少计算量。
通常许多子问题非常相似,为此动态规划法试图仅仅解决每个子问题一次,具有天然剪枝的功能,从而减少计算量:一旦某个给定子问题的解已经算出,则将其记忆化存储,以便下次需要同一个子问题解之时直接查表。这种做法在重复子问题的数目关于输入的规模呈指数增长时特别有用。
Easy难度
1 最大子序和
public int maxSubArray(int[] nums) {
int max=nums[0];
int temp=nums[0];
for(int i=1;i<nums.length;i++){
//当前和为负数,越加越小,直接使用当前值
if(temp<0)
temp=nums[i];
else
temp+=nums[i];
max=Math.max(max,temp);
}
return max;
}
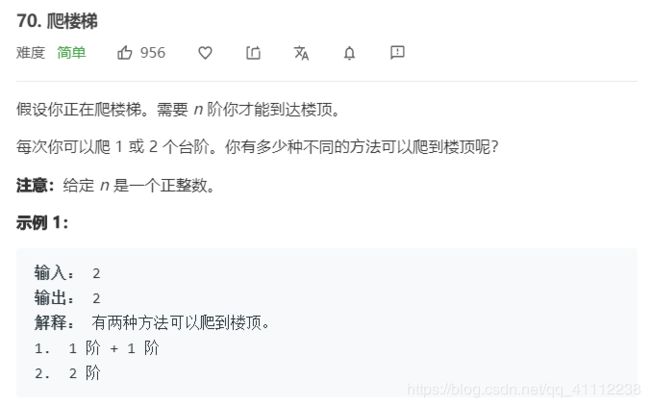
2 爬楼梯
public int climbStairs(int n) {
//经典题目了,爬到n的结果是n-1的结果加上n-2的结果
if(n==0||n==1||n==2)
return n;
int[] dp=new int[n+1];
dp[0]=0;
dp[1]=1;
dp[2]=2;
for(int i=3;i<n+1;i++){
dp[i]=dp[i-1]+dp[i-2];
}
return dp[n];
}
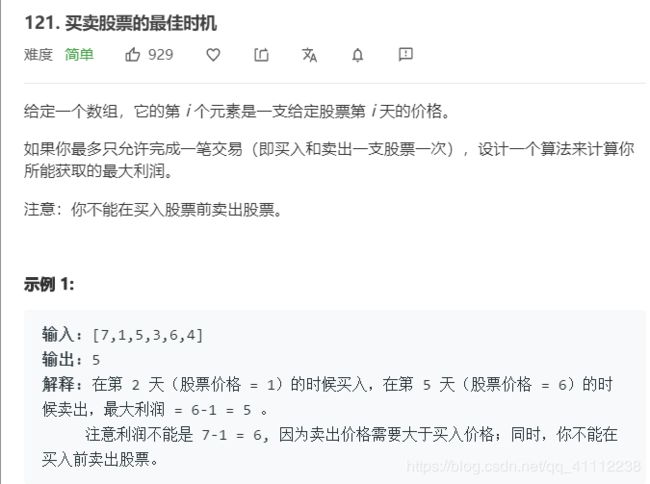
3 买卖股票的最佳时机
public int maxProfit(int[] prices) {
if(prices.length==0)
return 0;
int max=0;
int min=prices[0];
for(int i=1;i<prices.length;i++){
if(max<prices[i]-min)
max=prices[i]-min;
min=Math.min(min,prices[i]);
}
return max;
}
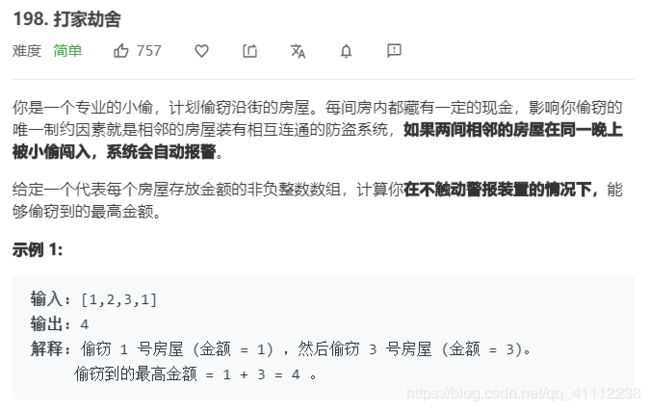
4 打家劫舍
public int rob(int[] nums) {
//dp[i]表示偷到第i家的最大金额,
//根据题意dp[i]=Math.max(dp[i-2]+nums[i],dp[i-1])
if(nums.length==0)
return 0;
if(nums.length==1)
return nums[0];
int[] dp=new int[nums.length+1];
dp[0]=0;//没有偷,金额0
dp[1]=nums[0];//偷到第一家,最高金额肯定就是第一家的金额
for(int i=2;i<nums.length+1;i++){
//由于dp中加了第0家的概念,因此对应nums[i-1]
dp[i]=Math.max(dp[i-2]+nums[i-1],dp[i-1]);
}
return dp[nums.length];
}
5 区域和检索-数组不可变
class NumArray {
//sum[i+1]表示nums[0]到nums[i]的和
private int[] sum;
public NumArray(int[] nums) {
sum=new int[nums.length+1];
for(int i=0;i<nums.length;i++){
sum[i+1]=sum[i]+nums[i];
}
}
public int sumRange(int i, int j) {
//sumRange(i,j)=sumRange(0,j)-sumRange(0,i-1)
return sum[j+1]-sum[i];
}
}
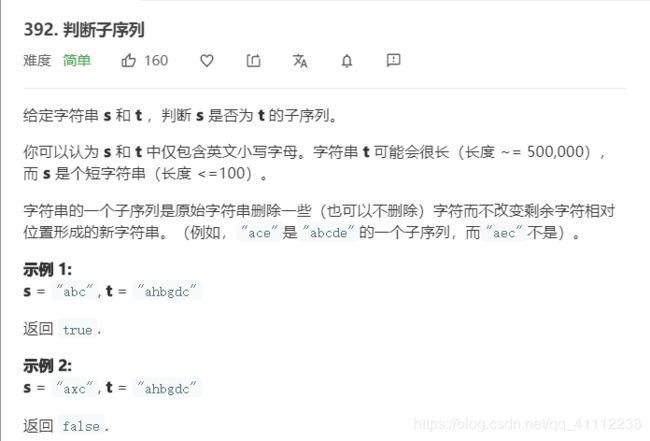
6 判断子序列
public boolean isSubsequence(String s, String t) {
int index=-1;
for(int i=0;i<s.length();i++){
char c=s.charAt(i);
//每次判断从当前索引的下一个开始,indexOf方法寻找从index+1开始第一个为c的索引
index=t.indexOf(c,index+1);
if(index==-1)
return false;
}
return true;
}
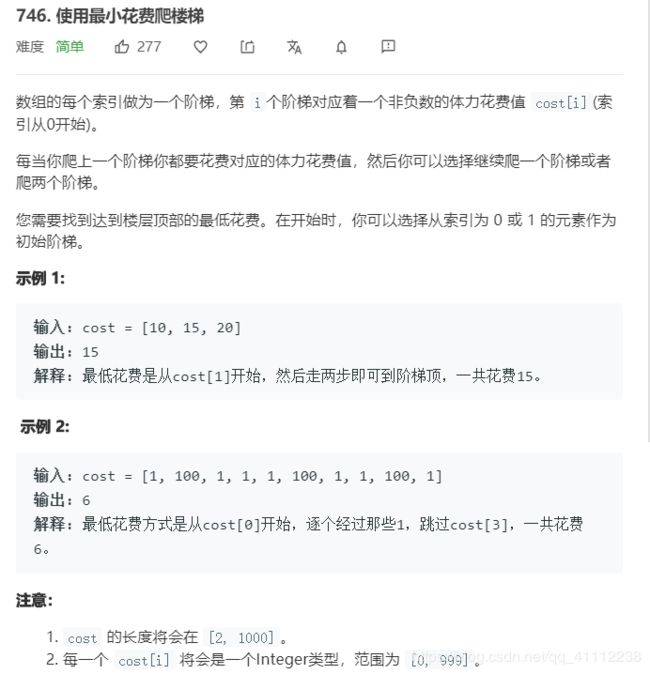
7 使用最小花费爬楼梯
public int minCostClimbingStairs(int[] cost) {
//动态规划
int[] dp=new int[cost.length];
dp[0]=cost[0];
dp[1]=cost[1];
for(int i=2;i<cost.length;i++)
dp[i]=Math.min(dp[i-1],dp[i-2])+cost[i];
return Math.min(dp[dp.length-1],dp[dp.length-2]);
}
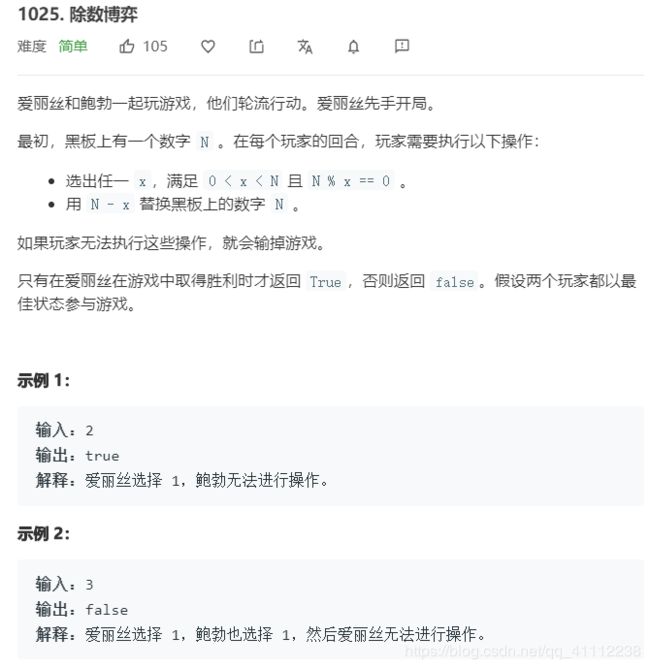
8 除数博弈
public boolean divisorGame(int N) {
//N为2时,赢,N为3时,输
//因此N为4时,只要取1个,就可以赢(对方是3,输)
//因此N为偶数可以赢,为奇数就输了
return N%2==0;
}
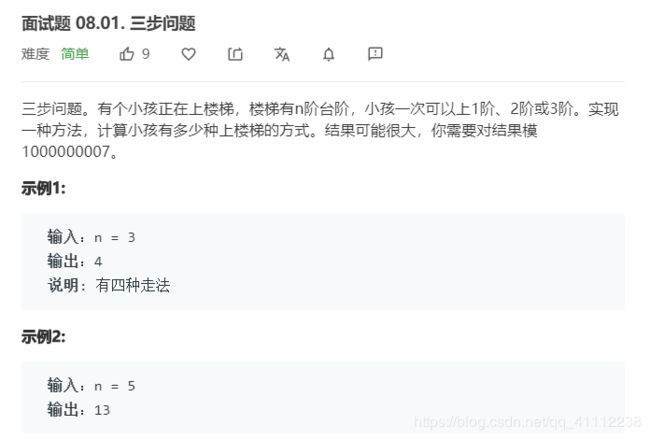
9 三步问题
public int waysToStep(int n) {
int num=1000000007;
//一楼一种:1,二楼两种1 1,2
if(n==1||n==2)
return n;
//三楼4种 1 1 1 1,1 2,2 1,3
if(n==3)
return 4;
//dp[i]表示i+1楼的方法数
int[] dp=new int[n];
dp[0]=1;
dp[1]=2;
dp[2]=4;
for(int i=3;i<dp.length;i++){
dp[i]=((dp[i-1]%num+dp[i-2]%num)%num+dp[i-3]%num)%num;
}
return dp[n-1];
}
10 按摩师
public int massage(int[] nums) {
if(nums.length==0)
return 0;
if(nums.length==1)
return nums[0];
int[] dp=new int[nums.length+1];
dp[0]=0;
dp[1]=nums[0];
for(int i=2;i<dp.length;i++){
dp[i]=Math.max(dp[i-2]+nums[i-1],dp[i-1]);
}
return dp[dp.length-1];
}
Medium难度
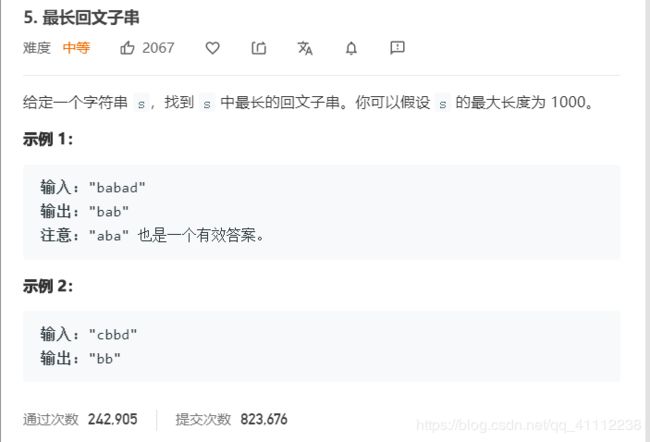
1 最长回文子串
public String longestPalindrome(String s) {
int len=s.length();
if(len<2)//长度为0或1,返回自己
return s;
int maxLen=1;
int start=0;
//dp[i][j]表示字符串s的i到j字串是否为回文串
boolean[][] dp=new boolean[len][len];
//初始化,单个字符串肯定是回文串
for(int i=0;i<dp.length;i++)
dp[i][i]=true;
//由于是回文串,只需要判断一半就行
for(int j=1;j<s.length();j++){
for(int i=0;i<j;i++){
//首尾不相等,肯定不是回文串,相等判断才继续判断
if(s.charAt(i)==s.charAt(j)){
if(j-i<3)//表示字串长度为0-2,首尾又相等,肯定是回文串
dp[i][j]=true;
else
dp[i][j]=dp[i+1][j-1];//除去首尾继续判断
}
if(dp[i][j]){//保持状态
len=j-i+1;
if(len>maxLen){
maxLen=len;
start=i;
}
}
}
}
//从start开始,长度为maxLen的字串就是结果
return s.substring(start,start+maxLen);
}
2 不同路径
public int uniquePaths(int m, int n) {
//n行m列
int[][] dp=new int[n][m];
//到第一行哪一列都m只有一种,就是向右走几个的问题
for(int i=0;i<m;i++)
dp[0][i]=1;
//到第一列哪一行都只有一种,就是向下走几个的问题
for(int i=0;i<n;i++)
dp[i][0]=1;
//到i行j列的路径数=到i-1行j列(上边格子)的数量+到i行j-1列(左边格子)的数量
for(int i=1;i<n;i++)
for(int j=1;j<m;j++)
dp[i][j]=dp[i-1][j]+dp[i][j-1];
return dp[n-1][m-1];
}
3 不同路径2
public int uniquePathsWithObstacles(int[][] dp) {
if(dp[0][0]==1)//第一个就是障碍物,不用计算了
return 0;
//行和列
int m=dp.length;
int n=dp[0].length;
//初始化第一行
int index=0;
//没遇到障碍物就初始化为0,障碍物及其之后都初始化0
while(index<n&&dp[0][index]!=1)
dp[0][index++]=1;
while(index<n){
dp[0][index++]=0;
}
//初始化第一列
index=1;
while(index<m&&dp[index][0]!=1)
dp[index++][0]=1;
while(index<m){
dp[index++][0]=0;
}
//动态规划填表
for(int i=1;i<m;i++){
for(int j=1;j<n;j++){
if(dp[i][j]==1)
dp[i][j]=0;//当前位置是障碍物,到达路径为0
else
dp[i][j]=dp[i-1][j]+dp[i][j-1];
}
}
return dp[m-1][n-1];
}
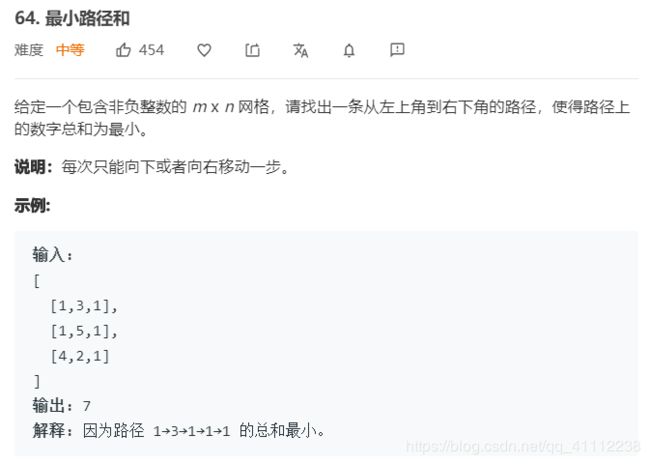
4 最小路径和
public int minPathSum(int[][] grid) {
//初始化第一行
for(int i=1;i<grid[0].length;i++){
grid[0][i]+=grid[0][i-1];
}
//初始化第一列
for(int i=1;i<grid.length;i++){
grid[i][0]+=grid[i-1][0];
}
//动态规划
for(int i=1;i<grid.length;i++){
for(int j=1;j<grid[0].length;j++){
grid[i][j]+=Math.min(grid[i-1][j],grid[i][j-1]);
}
}
return grid[grid.length-1][grid[0].length-1];
}
5 解码方法
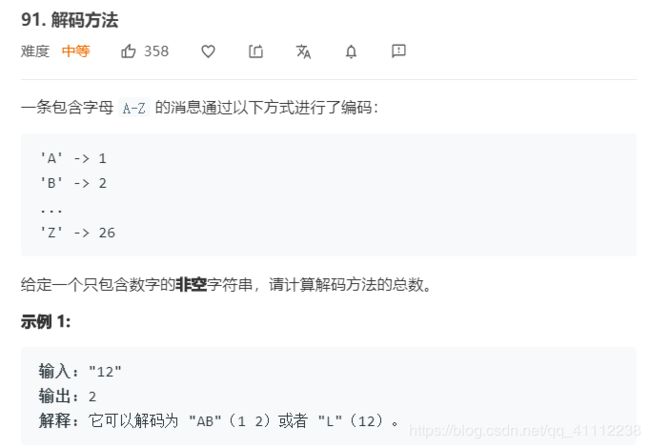
当前位置如果不为0,但不能和前一位数字组成1~26的数字,就等于前一位的解法数
例如1231的解法数=123的解法数
如果当前位置和前一位可以组成1~26的数字,就额外加上前两位的解法
例如1211的解法数=121的解法数+12的解法数
public int numDecodings(String s) {
if(s.charAt(0)=='0')
return 0;
//dp[i]表示到i-1位置为止的解密方法数
int[] dp=new int[s.length()+1];
dp[0]=1;
dp[1]=1;
for(int i=2;i<dp.length;i++){
if(s.charAt(i-1)!='0')
dp[i]=dp[i-1];
if(s.charAt(i-2)=='1'||(s.charAt(i-2)=='2'&&s.charAt(i-1)<='6'))
dp[i]+=dp[i-2];
}
return dp[dp.length-1];
}
6 不同的二叉搜索树
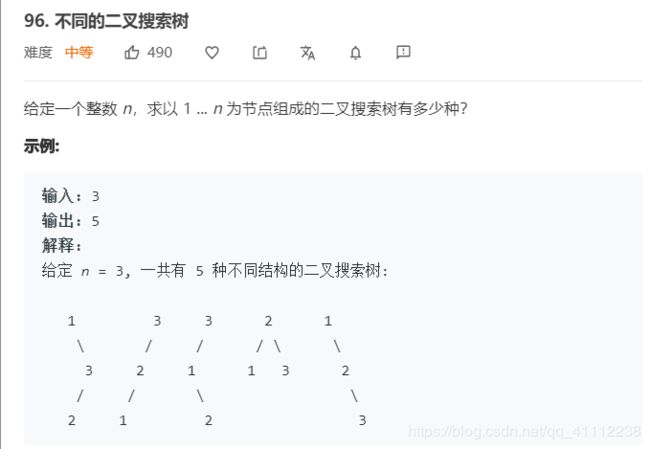
设dp[N]为1-N的不同二叉树个数,而f(i)是以i为节点的不同二叉树个数,那么dp[N]=f(1)+f(2)+…+f(n),f(i)=dp(i-1)*dp(N-i),因为左边有i-1个节点,右边有N-i个节点。
根据此关系写代码:
public int numTrees(int n) {
int[] dp=new int[n+1];
dp[0]=1;
dp[1]=1;
for(int N=2;N<=n;N++){
for(int i=1;i<N+1;i++){
dp[N]+=dp[i-1]*dp[N-i];
}
}
return dp[n];
}
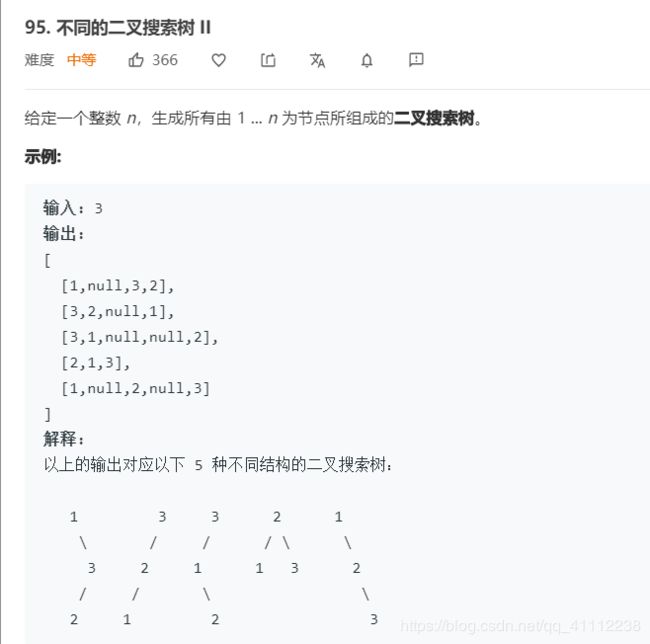
7 不同的二叉搜索树2
public List<TreeNode> generateTrees(int n) {
if(n==0)
return new ArrayList<TreeNode>();
return generateTrees(1,n);
}
private List<TreeNode> generateTrees(int start, int end) {
List<TreeNode> list=new ArrayList<>();
if(start>end){
list.add(null);
return list;
}
for(int i=start;i<=end;i++){
//以i为根节点,i左边为左子树,i右边为右子树
List<TreeNode> leftList=generateTrees(start,i-1);
List<TreeNode> rightList=generateTrees(i+1,end);
for(TreeNode lChild:leftList){
for(TreeNode rChild:rightList){
TreeNode node = new TreeNode(i);
node.left=lChild;
node.right=rChild;
list.add(node);
}
}
}
return list;
}
8 三角形最小路径和
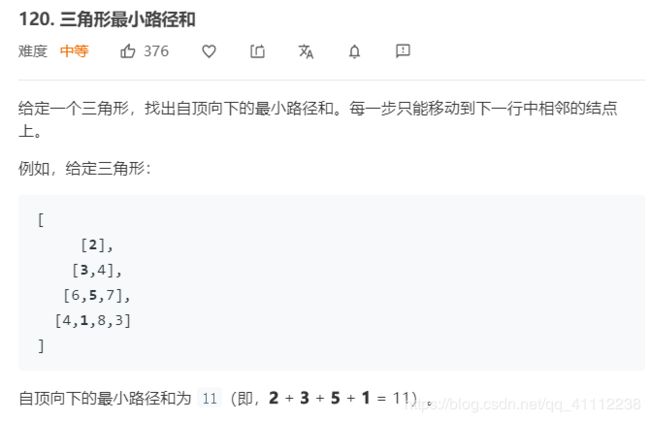
如果是边界的两个值,那么最小值就是上面边界的累加值加上自己,否则就是两边的较小值加上自己,最后把最后一行遍历,寻找最小值即可。
public int minimumTotal(List<List<Integer>> triangle) {
int n=triangle.size();
int[][] dp=new int[n][n];
dp[0][0]=triangle.get(0).get(0);
for(int i=1;i<n;i++){
List<Integer> list = triangle.get(i);
for(int j=0;j<=i;j++){
if(j==0) {//左边界
dp[i][j] = dp[i-1][j] + list.get(j);
}else if(j==i){//右边界
dp[i][j] = dp[i-1][j-1] + list.get(j);
}else {
dp[i][j] = Math.min(dp[i-1][j-1],dp[i-1][j])+list.get(j);
}
}
}
int min=Integer.MAX_VALUE;
for(int j=0;j<n;j++){
if(dp[n-1][j]<min)
min=dp[n-1][j];
}
return min;
}
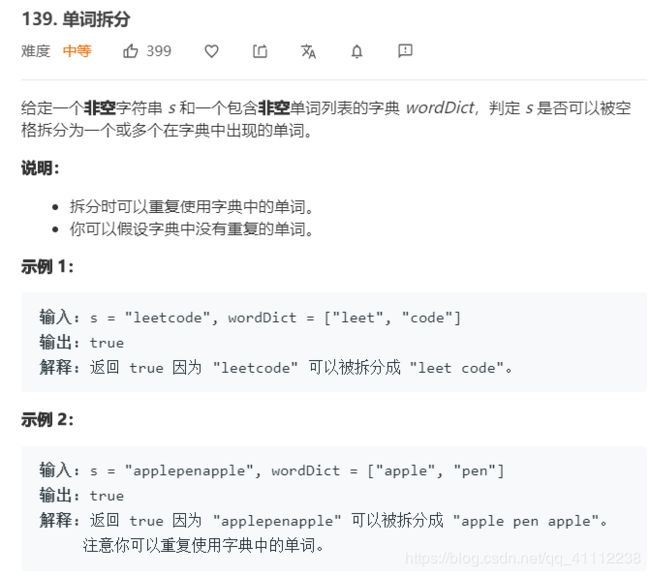
9 单词拆分
public boolean wordBreak(String s, List<String> wordDict) {
//去重
HashSet<String> set = new HashSet<>(wordDict);
//dp[i]表示到i+1位置截至,是否可成功拆分
boolean[] dp=new boolean[s.length()+1];
dp[0]=true;
for(int i=1;i<dp.length;i++){
for(int j=0;j<i;j++){
if(dp[j]&&set.contains(s.substring(j,i))){
dp[i]=true;
break;
}
}
}
return dp[dp.length-1];
}
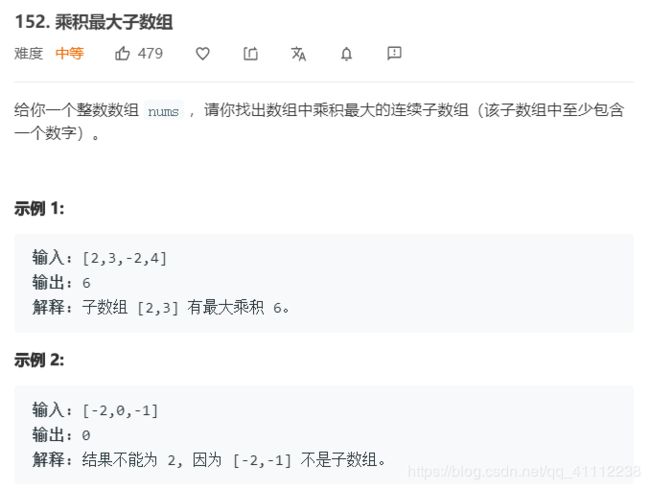
10 乘积最大子数组
public int maxProduct(int[] nums) {
int max=Integer.MIN_VALUE;
int tmpMax=1;
int tmpMin=1;
for(int i=0;i<nums.length;i++){
if(nums[i]<0){
int tmp=tmpMax;
tmpMax=tmpMin;
tmpMin=tmp;
}
tmpMax=Math.max(tmpMax*nums[i],nums[i]);
tmpMin=Math.min(tmpMin*nums[i],nums[i]);
max=Math.max(tmpMax,max);
}
return max;
}
11 打家劫舍2
相等于计算两边打家劫舍1,范围是第一个到倒数第二个,或者第二个到最后一个
public int rob(int[] nums) {
if(nums.length==0)
return 0;
if(nums.length==1)
return nums[0];
int max1=robHelp(Arrays.copyOfRange(nums,0,nums.length-1));
int max2=robHelp(Arrays.copyOfRange(nums,1,nums.length));
return Math.max(max1,max2);
}
public int robHelp(int[] nums) {
int[] dp=new int[nums.length+1];
dp[0]=0;
dp[1]=nums[0];
for(int i=2;i<nums.length+1;i++){
dp[i]=Math.max(dp[i-2]+nums[i-1],dp[i-1]);
}
return dp[nums.length];
}
12 最大正方形
public int maximalSquare(char[][] matrix) {
int maxLen=0;
int row=matrix.length;
int col=row>0?matrix[0].length:0;
int[][] dp=new int[row+1][col+1];
for(int i=1;i<=row;i++){
for(int j=1;j<=col;j++){
if(matrix[i-1][j-1]=='1'){
dp[i][j]=Math.min(dp[i-1][j],Math.min(dp[i-1][j-1],dp[i][j-1]))+1;
maxLen=Math.max(maxLen,dp[i][j]);
}
}
}
return maxLen*maxLen;
}
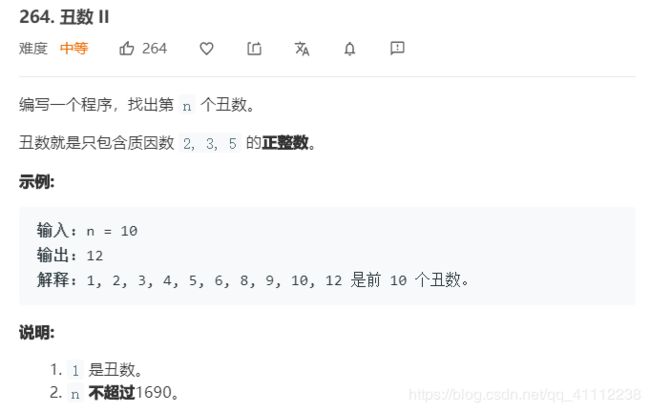
13 丑数
public int nthUglyNumber(int n) {
int[] dp=new int[n];
dp[0]=1;
int index2=0;
int index3=0;
int index5=0;
for(int i=1;i<n;i++){
int min2=dp[index2]*2;
int min3=dp[index3]*3;
int min5=dp[index5]*5;
int min=Math.min(min2,Math.min(min3,min5));
dp[i]=min;
if(min==min2)
index2++;
if(min==min3)
index3++;
if(min==min5)
index5++;
}
return dp[n-1];
}
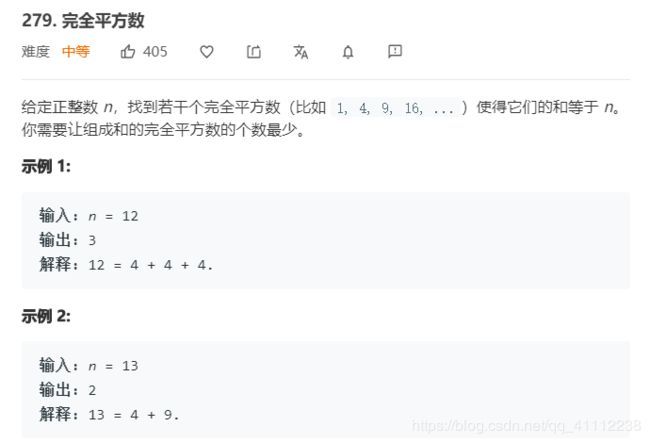
14 完全平方数
public int numSquares(int n) {
int[] dp=new int[n+1];
dp[0]=0;
dp[1]=1;
for(int i=2;i<dp.length;i++){
dp[i]=i;
for(int j=1;i-j*j>=0;j++){
dp[i]=Math.min(dp[i],dp[i-j*j]+1);
}
}
return dp[n];
}
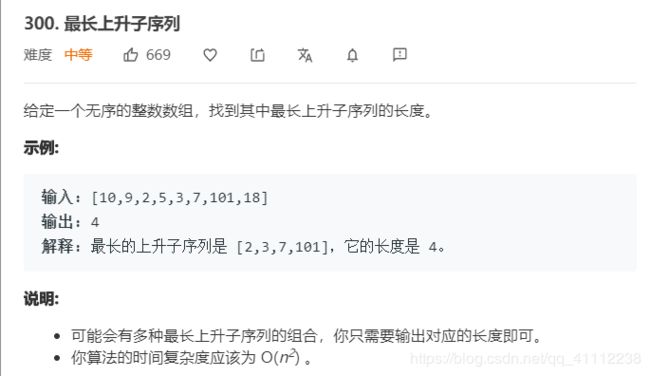
15 最长上升子序列
public int lengthOfLIS(int[] nums) {
if(nums.length==0)
return 0;
int[] dp=new int[nums.length];
Arrays.fill(dp,1);
//保持最大值
int res=1;
for(int i=1;i<dp.length;i++){
for(int j=0;j<i;j++){
if(nums[j]<nums[i])
dp[i]=Math.max(dp[i],dp[j]+1);
}
res=Math.max(res,dp[i]);
}
return res;
}