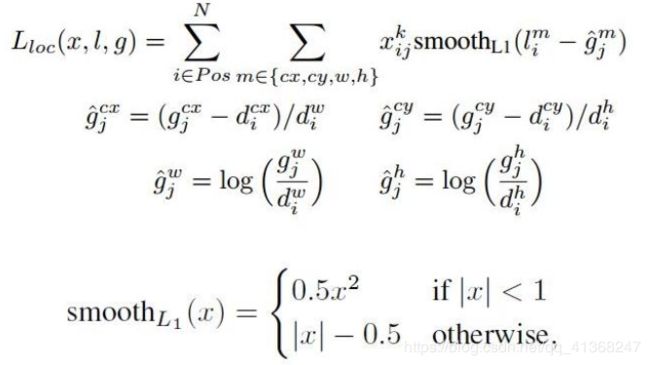目标检测算法——SSD详解

 

目录

一、 背景（基本介绍）

二、 网络结构

三、 具体过程

1. default box 匹配

2. 损失函数

3. 数据增广

4. Atrous Algothrim

5.  NMS（非极大值抑制）

 五、 性能评估

优点：

缺点：

SSD 算法的改进：DSSD

1. DSSD 网络结构

图19 VGG网络与ResNet网络的对比

2. 实现细节

3. 训练与预测

4. 总结

DSSD 检测结果展示

---

一、 背景（基本介绍）

基于“Proposal + Classification”的目标检测方法中，R-CNN 系列（R-CNN、 SPPnet、

Fast R-CNN以及 Faster R-CNN等）取得了非常好的结果，但是在速度方面离实时效果还比较远。在提高 mAP (Mean Average Precision) 的同时兼顾速度，逐渐成为神经网络目标检测领域未来的趋势。YOLO检测算法不仅能够达到实时的效果，而且mAP与前面面提到的 RCNN系列相比有很大的提升。 但是YOLO 有一些缺陷：每个网格只能预测一个物体，容易造成漏检；且对于物体的尺度相对比较敏感，面对尺度变化较大的物体时泛化能力较差。针对

YOLO 中的这些不足，SSD(Single Shot MultiBox Detector)网络在这两方面都有所改进，同时兼顾了 mAP 和实时性的要求。

two-stage 方法与 one-stage 方法

主流的算法主要分为两个类型：

1. two-stage方法：如R-CNN系列算法，其主要思路是先通过启发式方法（selective search）或者 CNN 网络（RPN)产生一系列稀疏的候选框，然后对这些候选框进行分类(classification)与回归(bounding box regression)，two-stage方法的优势是准确度高； 
2. one-stage方法：如YOLO和SSD，其主要思路是均匀地在图片多个层数的特征图上进行密集抽样，抽样时可以采用不同尺度和长宽比，然后利用CNN提取特征后直接进行分类与回归，整个过程只需要一步，所以其优势是速度快。但是均匀的密集采样的一个重要缺点

是训练比较困难，这主要是因为正样本与负样本（背景）极其不均衡，导致模型准确度稍低。

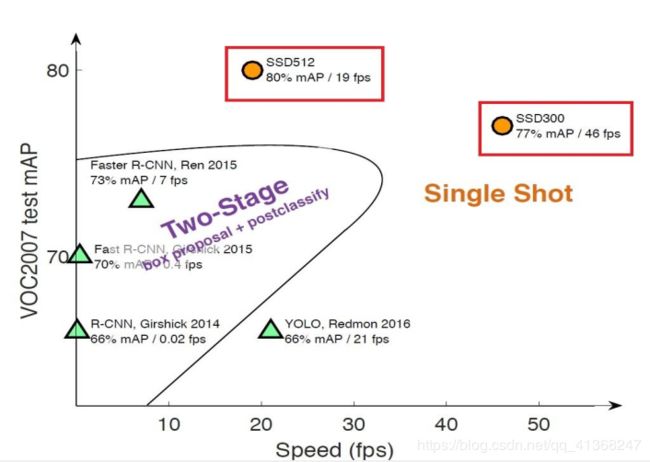
不同算法的性能如图1所示，可以看到两类方法在准确度和速度上的差异。

图 1 不同检测算法的性能对比

 

二、 网络结构

共有两种SSD网络：SSD 300和SSD 512，用于不同输入尺寸的图像识别。下文主要以 SSD 300为例进行分析。

图 2 SSD 300 网络总体架构

SSD 300 中输入图像的大小是 300x300，特征提取部分使用了 VGG16 的卷积层，并将 VGG16的两个全连接层转换成了普通的卷积层（图中conv6和conv7），之后又接了多个卷积（conv8_1，conv8_2，conv9_1，conv9_2，conv10_1，conv10_2），最后用一个Global Average Pool来变成1x1的输出（conv11_2）。 从图中我们可以看出，SSD将conv4_3、conv7、conv8_2、conv9_2、conv10_2、conv11_2都连接到了最后的检测分类层做回归。具体细节如图3：

图 3 SSD 300 网络中多个特定 feature map 同时进行回归分类

 

     观察上述两幅图，我们可以初步得到SSD网络预测过程的基本步骤：

1. 输入一幅图片（300x300），将其输入到预训练好的分类网络（改进的传统的VGG16 网络）中来获得不同大小的特征映射；
2. 抽取Conv4_3、Conv7、Conv8_2、Conv9_2、Conv10_2、Conv11_2层的feature map，然后分别在这些feature map层上面的每一个点构造6个不同尺度大小的Default boxes。然后分别进行检测和分类，生成多个初步符合条件的Default boxes；
3. 将不同feature map获得的Default boxes结合起来，经过NMS（非极大值抑制）方法来抑制掉一部分重叠或者不正确的Default boxes，生成最终的Default boxes 集合（即检测结果）；

这是通过观察 SSD 网络结构得出的大概流程，其中具体的训练过程与相关概念将在下一部分进行介绍。

三、 具体过程

首先列出SSD的三条核心设计理念：

1. 采用多尺度特征图用于检测

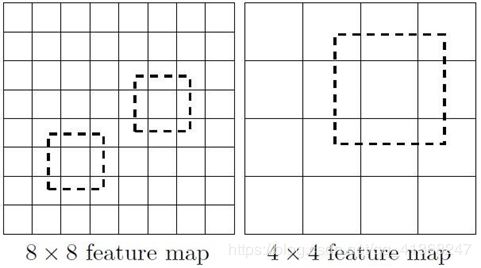
所谓多尺度采用大小不同的特征图，CNN网络一般前面的特征图比较大，后面会逐渐采用stride=2的卷积或者pool来降低特征图大小，这正如图3所示，一个比较大的特征图和一个比较小的特征图，它们都用来做检测。这样做的好处是比较大的特征图来用来检测相对较小的目标，而小的特征图负责检测大目标，如图4所示，8x8的特征图可以划分更多的单元，但是其每个单元的先验框尺度比较小。

图4 不同尺度的特征图标题

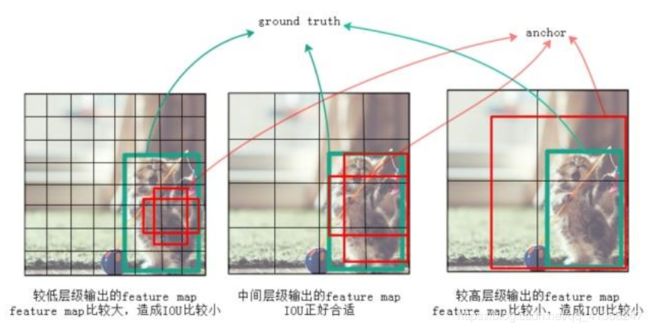
而其作用可以从图5的例子中得到很好的体现。图5(a)中，浅层网络特征图很适合用来识别猫这一目标（蓝色方框），但面对狗这一目标，选框尺寸显得太小无法很好地将目标检测到。而到了深层网络，由于特征图经过池化层后尺寸减小，感受野变大。因此，红色选框可以较准确地识别到狗。究其原因，正是因为每一个特征图中都只能用尺度相同的选框（应称为Default boxes，后文会介绍），导致目标尺寸与选框尺寸差距过大时，无法完成理想检测。

从图5(b)中更是可以直接感受到，采用多尺度特征用于检测可以提高识别的准确度。

(a)

(b)
图 5 多尺度特征图检测的作用

2. 设置Default boxes

SSD借鉴了Faster R-CNN中anchor（如图6）的理念，每个单元设置尺度或者长宽比不同的Default boxes，预测的边界框（bounding boxes）是以这些Default boxes为基准的，在一定程度上减少训练难度。一般情况下，每个单元会设置多个先验框，其尺度和长宽比存在差异。

对应上一条核心思想我们知道，Default boxes其实就是在某一feature map上每一点处选取的不同长宽比的选框。与YOLO不同的是，YOLO在每个位置只选取正方形选框，但是真实目标的形状是多变的，Yolo需要在训练过程中自适应目标的形状。

 图6 Faster R-CNN中的anchor

 

Default boxes 尺寸的确定

Conv7，Conv8_2，Conv9_2，Conv10_2，Conv11_2作为检测所用的特征图，加上Conv4_3层，共提取了6个特征图，其大小分别是(38,38)(19,19)(10,10)(5,5)(3,3)(1,1)。但是不同特征图设置的先验框数目不同。先验框的设置，包括尺度（scale）和长宽比（aspect ratio）两个方面。对于先验框的尺度，其遵守一个线性递增规则：随着特征图大小降低，先验框尺度线性增加：

这里smin是0.2，表示最底层的尺度是0.2,；smax是0.9，表示最高层的尺度是0.9。通过这种计算方法，可以得出6个特征图的default box尺度分别为：[30,60,111,162,213,264]。长宽比用??表示为下式（注意这里一共有5种长宽比）： 

 通过下面的公式计算 default box 的宽度w和高度h:

默认情况下，每个特征图会有一个?? =1且尺度为??的先验框，除此之外，还会设置一个尺度为

的先验框，这样每个特征图都设置了两个长宽比为1但大小不同的正方形先验框。因此，每个特征图一共有6个先验框，但是在实现时，Conv4_3，Conv10_2和Conv11_2层仅使用4个先验框，它们不使用长宽比为3,1/3的先验框。

SSD300一共可以预测的default box个数为：

 所以说SSD本质上是密集采样。

 

3. 采用卷积进行检测

与 Yolo最后采用全连接层不同，SSD直接采用卷积对不同的特征图来进行提取检测结果。

对网络中 6 个特定的卷积层的输出分别用两个 3*3 的卷积核进行卷积，一个输出分类用的confidence，每个default box生成21个confidence（这是针对VOC数据集包含20 个 object 类别而言的，另外一个是背景的分类）；一个输出回归用的 localization，每个 default box生成4个坐标值（x，y，w，h）。

图7给出了一个5*5大小的特征图的检测过程。其中Priorbox是代表default box（只是不同叫法，实际上是一样的），前面已经介绍了生成规则。检测值包含两个部分：类别置信度和边界框位置，各采用一次 3*3 卷积来进行完成。令??为该特征图所采用的先验框数目，那么类别置信度需要的卷积核数量为?? × ?，而边界框位置需要的卷积核数量为?? × 4。

图 7 使用 3*3 卷积核对 feature map 进行处理

 

1. default box 匹配

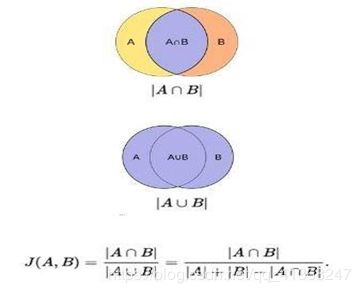
在训练过程中，首先要确定训练图片中的ground truth（真实目标）与哪个先验框来进行匹配，与之匹配的先验框所对应的边界框将负责预测它。在YOLO中，ground truth的中心落在哪个单元格，该单元格中与其IOU(定义见图8)最大的边界框负责预测它。但是在SSD 中却完全不一样，SSD的先验框与ground truth的匹配原则主要有两点。在训练时，ground truth与 default boxes按照如下方式进行配对：

• 首先，寻找与每一个ground truth box有最大IoU的default box，这样就能保证每一个ground truth能与至少一个default box对应起来。
• SSD之后又将剩余还没有配对的default box与任意一个ground truth尝试配对，只要两者之间的IoU大于阈值，就进行匹配（SSD 300 阈值为0.5）。

通常称与ground truth匹配的default box为正样本，反之，若一个default box没有与任何ground truth进行匹配，那么该default box只能与背景匹配，就是负样本。图 9为一个匹配示意图，其中绿色的GT是ground truth，红色为先验框，FP表示负样本，TP 表示正样本。

 图8 IoU的定义（即图中J(A, B)）

 

图9 正样本(TP)与负样本(FP)

 

尽管一个ground truth可以与多个先验框匹配，但是ground truth相对先验框还是太少了，所以负样本相对正样本会很多。为了保证正负样本尽量平衡，SSD 采用了 hard negative mining，就是对负样本进行抽样，抽样时按照置信度误差（预测背景的置信度越小，误差越大）进行降序排列，选取误差的较大的top-k作为训练的负样本，以保证正负样本比例接近1:3。

 

2. 损失函数

在训练样本确定了之后，就是选择损失函数了。损失函数定义为位置误差（locatization loss， loc）与置信度误差（confidence loss, conf）的加权和：

其中N是先验框的正样本数量。c为类别置信度预测值。l 为先验框的所对应边界框的位置预测值，而g是ground truth的位置参数。权重系数α通过交叉验证设置为1。

• 对于位置误差，其采用Smooth L1 loss，定义如下：

  

这里???? ∈ {1,0}为一个指示参数，当???? = 1时表示第i个default boxes与第j个ground truth匹配，并且ground truth的类别为g。由于????的存在，所以位置误差仅针对正样本进行计算。

• 对于置信度误差，其采用softmax loss，定义如下：

     从公式中可以看出，置信度的误差包含两个部分：正样本的误差和负样本的误差。通过图11我们可以更好地观察到具体过程。

 

3. 数据增广

不同于Faster R-CNN，SSD算法使用了多种数据增强的方法，包括水平翻转、裁剪、放大和缩小等。论文明确指出，数据增强可以明显的提高算法的性能。主要的目的是为了使得该算法对输入的不同大小和不同形状的目标具有更好的鲁棒性。直观的理解是通过这个数据增强操作可以增加训练样本的个数，同时构造出更多的不同形状和大小的目标，将其输入到网络中，可以使得网络学习到更加鲁棒的特征。

图10 水平翻转、裁剪、放大和缩小等数据增强的方法

图 11 正样本与负样本分别进行误差计算

 

4. Atrous Algothrim

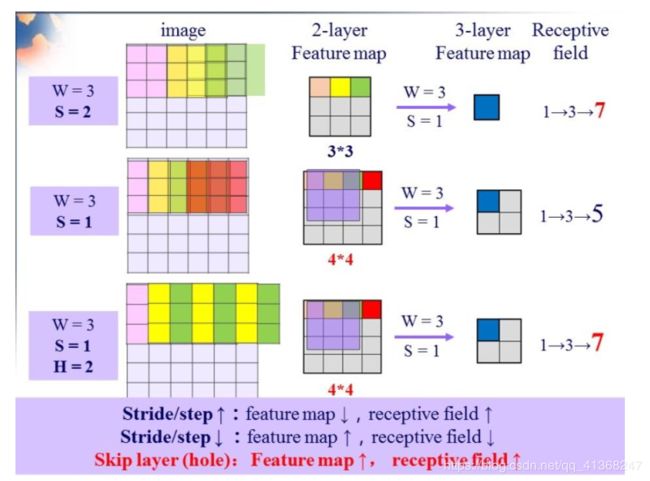
采用 Hole 算法可以利用已经训练好的模型进行微调，又可以改变网络结构得到更加稠密的得分图。其原理如图12。

图 12 Hole 算法扩大感受野

 

图 13 Hole 算法在增加特征图尺寸的同时扩展感受野

 

5.  NMS（非极大值抑制）

在 SSD 算法中，NMS 至关重要。因为多个 feature map 最后会产生大量的 bounding boxes，即最终检测结果。然而在这些bounding boxes中存在着大量的错误的、重叠的、不准确的样本，这不仅造成了巨大的计算量，如果处理不好会影响算法的性能。仅仅依赖于IOU 是不现实的，IOU值设置的太大，可能就会丢失一部分检测的目标，即会出现大量的漏检情况；IOU值设置的太小，则会出现大量的重叠检测，会大大影响检测器的性能。

即使在IOU处理掉大部分的bounding boxes之后，仍然会存在大量的错误的、重叠的、不准确的bounding boxes（如图14），这就需要NMS进行迭代优化。

图14 重叠的、IoU无法剔除的bounding boxes

NMS简单原理：  对于Bounding Box的列表B及其对应的置信度S,采用下面的计算方式.选择具有最大 score的检测框M,将其从B集合中移除并加入到最终的检测结果D中.通常将B中剩余检测框中与M的IoU大于阈值的框从B中移除.重复这个过程,直到B为空。

 

预测过程

预测过程比较简单，对于每个预测框(default boxes)，首先根据类别置信度确定其类别（置信度最大者）与置信度值，并过滤掉属于背景的预测框。然后根据置信度阈值（如0.5）过滤掉阈值较低的预测框。对于留下的预测框进行解码，根据先验框得到其真实的位置参数，一般需要根据置信度进行降序排列，然后仅保留top-k（如400）个预测框。最后就是进行

NMS算法，过滤掉那些重叠度较大的预测框。最后剩余的预测框就是检测结果了。

图 15 使用分类网络给出每个框的每类置信度,使用回归网络修正位置,最终应用 NMS

图15中，（2）中黄色bounding boxes可以代表为正样本。正样本通过分类与回归得到（3）中的各色bounding boxes，到这一步时使用了top-k让选框数量减少。最后再使用NMS 得到（4）。

 

 五、 性能评估

1. 模块性能

图16 SSD训练过程各模块对性能的影响

观察上图可以得到如下的结论：

• • 数据增强方法在SSD算法中起到了关键性的作用，使得mAP从65.5变化到71.6，主要的原因可能是数据增强增加了样本的个数，使得模型可以获得更重更样的样本，即提高了样本的多样性，使得其具有更好的鲁棒性，从而找到更接近GT的bounding boxes。
  • [1/2，2]和[1/3, 3]box可以在一定程度上提升算法的性能，主要的原因可能是这两种box可以在一定程度上增加较大和较小的bounding boxes，可以更更加准确的检测到较大和较小的目标，而且VOC数据集上面的目标一般都比较大。当然，更多的比例可以进一步提升算法的性能。
  • Atrous算法可以轻微提升算法性能，但是其主要的作用是用来提速，论文中表明它可以提速20%。主要的原因可能是虽然该算法可以获得更大的feature map和感受野，但是由于SSD本身利用了多个feature map来获取bounding boxes，bounding boxes的多样性已经足够，由于feature map扩大而多得到的bounding boxes可能是一些重复的，并没有起到提升检测性能的作用。

 

1. SSD 加速的原因
   • 原因 1：首先 SSD 是一个 one-stage 网络，只需要一个阶段就可以输出结果；而 Faster R-CNN是一个two-stage网络。尽管Faster R-CNN的bounding boxes少很多，但是其需要大量的前向和反向推理（训练阶段），而且需要交替的训练两个网络；
   • 原因2：Faster R-CNN中不仅需要训练RPN，而且需要训练Fast R-CNN，而SSD其实相当于一个优化了的RPN网络，不需要进行后面的检测，仅仅前向推理就会花费很多时间；
   • 原因3：YOLO网络虽然比SSD网络看起来简单，但是YOLO网络中含有大量的全连接层。和FC层相比，CONV层具有更少的参数；同时YOLO获得候选bounding boxes的操作比较费时；SSD算法中，调整了VGG网络的架构，将其中的 FC 层替换为 CONV 层，这一点会大大的提升速度。
   • 原因4：使用了Atrous算法，该算法能够提速20%。
   • 原因5：SSD设置了输入图片的大小，它会将不同大小的图片裁剪为300x300，或者

512x512，和Faster-rcnn相比，在输入上就会少很多的计算。

 

1. 优缺点

优点：

 运行速度超过YOLO，精度超过Faster R-CNN（一定条件下，对于稀疏场景的大目标而言）。

缺点：

• 需要人工设置default boxes的初始尺度和长宽比的值。网络中default boxes的基础大小和形状不能直接通过学习获得，而是需要手工设置。而网络中每一层 feature使用的default box大小和形状恰好都不一样，导致调试过程非常依赖经验。
• 对小尺寸的目标识别仍比较差，还达不到 Faster R-CNN 的水准。因为 SSD 使用 conv4_3 低级 feature 去检测小目标，而低级特征卷积层数少，存在特征提取不充分的问题。

 

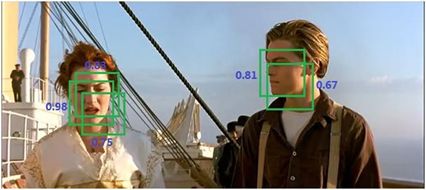
SSD 检测结果展示：

 

SSD 算法的改进：DSSD

SSD算法的局限：

卷积神经网络在结构上存在固有的问题：高层网络感受野比较大，语义信息表征能力强，但是分辨率低，几何细节信息表征能力弱。低层网络感受野比较小，几何细节信息表征能力强，虽然分辨率高，但语义信息表征能力弱。

SSD采用多尺度的特征图来预测物体，使用具有较大感受野的高层特征信息预测大物体，具有较小感受野的低层特征信息预测小物体。

这样就带来一个问题：使用的低层网络的特征信息预测小物体时，由于缺乏高层语义特征，导致SSD对于小物体的检测效果较差。而解决这个问题的思路就是对高层语意信息和低层细节信息进行融合。DSSD采用Top Down的网络结构进行高低层特征的融合并且改进了传统上采样的结构。

DSSD算法思想：

DSSD使用一种通用的Top Down的融合方法，使用VGG和Resnet网络，以及不同大小的训练图片尺寸来验证算法的通用性。

将高层的语义信息融入到低层网络的特征信息中，丰富预测回归位置框和分类任务输入的多尺度特征图，以此来提高检测精度。

在提取出多尺度特征图之后，DSSD 提出由残差单元组成的预测模块，进一步提取深度的特征最后输入给框回归任务和分类任务。

 

1. DSSD 网络结构

图 18 DSSD 网络结构

DSSD的基础是SSD检测网络。经过以上的分析我们知道，SSD算法对小目标不够鲁棒的最主要的原因是浅层feature map的表征能力不够强。

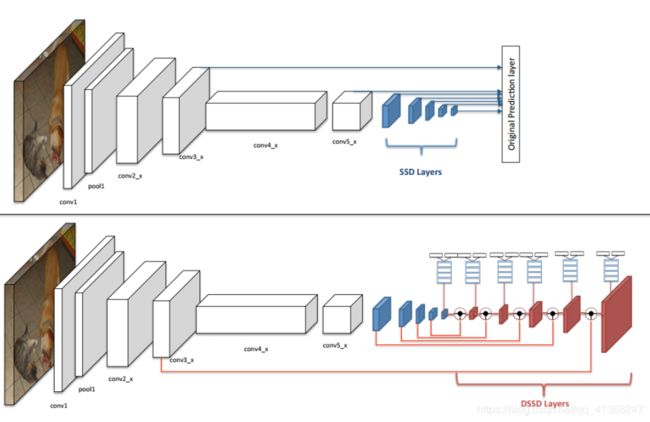
DSSD 就使用了更好的基础网络（ResNet）和 Deconvolution 层，skip 连接来给浅层 feature map更好的表征能力。（图18上半部分）。

 

图19 VGG网络与ResNet网络的对比

DSSD算法将图18中的特定的七层特征图拿出六层（去掉尺寸最小的一层的特征图）输入到反卷积模型里，输出修正的特征图金字塔，形成一个由特征图组成的沙漏结构。最后经预测模块输入给框回归任务和分类任务做预测。

图18基本上展示了DSSD的核心思想，也就是如何利用中间层的上下文信息。

方法就是把红色层做反卷积操作，使其和上一级蓝色层尺度相同，再把二者融合在一起，得到的新的红色层用来做预测。如此反复，仍然形成多尺度检测框架。在图中越往后的红色层分辨率越高，而且包含的上下文信息越丰富，综合在一起，使得检测精度得以提升。

 

2. 实现细节

1. 预测模块

SSD的直接从数个卷积层中分别引出预测函数，预测量多达7000多，梯度计算量也很大。 MS-CNN 方法指出，改进每个任务的子网可以提高准确性。根据这一思想，作者在每一个预测层后增加残差模块，并且对于多种方案进行了对比，如下图所示。

 

图 19 预测模型结构

图中：

1. 1. (a)为SSD使用的方法，直接提取出网络中的多尺度特征图做分类和回归的预测；
   2. (b)为Resnet残差单元的网络结构；
   3. (c)为改进的只含一个残差单元的预测模型，在残差旁路将原来的特征图用的卷积核做处理后与网络主干道的特征图做通道间加法；
   4. (d)为只含两个残差单元的预测模型。

图中四种预测方式的实验结果如下图： 

图20 四种预测模型实验结果

结果表明，增加残差预测模块后，高分辨率图片的检测精度比原始SSD提升明显。

1. 反卷积模块

为了引入更多的高级上下文信息，DSSD在SSD+Resnet-101之上，采用反卷积层来进行预测(Deconvolution Module)。和原始SSD是不同的，最终形成沙漏形的网络。添加额外的反卷积层以连续增加后面特征图的分辨率，为了加强特征，作者在沙漏形网络中采用了跳步连接（skip connection）方法。

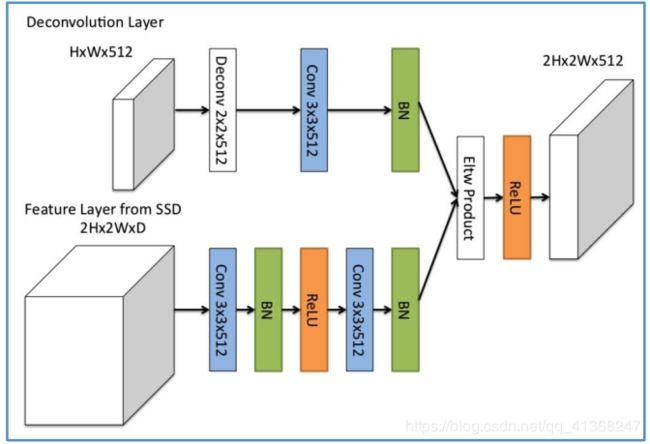
反卷积模型指的是DSSD中高层特征和低层特征的融合模块，其基本结构如下图 21所示。该模块可以适合整个DSSD架构（图18底部实心圆圈）

图 21 反卷积模块基本结构

DSSD 的提出者认为用于精细网络的反卷积模块的分解结构达到的精度可以和复杂网络一样，并且更有效率。因此进行了一定的改进，如图21所示：

1. 在每个卷积层后添加批归一化层；
2. 使用基于学习的反卷积层而不是简单地双线性上采样；
3. 测试了不同的结合方式，元素求和（element-wise sum）与元素点积（element-wise product）方式，实验证明点积计算能得到更好的精度(见图22)。

图22 元素求和与元素点积方法效果对比

 

3. 训练与预测

a) 训练过程

训练的大部分过程和原始SSD类似。

1. 首先，依然采用了SSD的default boxes，把重叠率高于0.5的视为正样本。
2. 设置一些负样本，使得正负样本的比例为3:1。
3. 训练中使Smooth L1+Softmax联合损失函数最小。训练前依然需要数据扩充（包含了hard example mining技巧）。

另外原始SSD的default boxes维度是人工指定的，可能不够高效，为此，DSSD算法在这里采用K-means聚类方法重新得到了7种default boxes维度，得到的这些boxes维度更具代表性。这一点是对上文提到的SSD算法需要人工确定default boxes，很依赖经验这一局限的改进。

而训练阶段DSSD算法独有的过程分为两个阶段：

第一个阶段，加载SSD模型初始化DSSD网络，并冻结SSD网络的参数，然后只增加反卷积模型(不添加预测模型)，在这样的条件下只训练反卷积模型；

第二个阶段，微调第一阶段的模型，解冻第一阶段训练时候冻结的所有参数，并添加预测模型。

b) 预测过程

预测过程较 SSD 算法并无太大差别。同样是选取特定层的 feature map 选取 default boxes。但需要注意的是，由于经过了反卷积层的作用，这些feature map包涵更多的特征信息和更精细的感受野。

对选定的feature map使用新增加的残差模块进行运算后，再做分类与回归（SSD中没有残差模块）。

接着就是SSD算法的流程了，根据置信度进行降序排列保留top-k个预测框。然后进行

NMS 算法，过滤掉那些重叠度较大的预测框。最后剩余的预测框就是检测结果了。见下图。

 图23 DSSD预测过程

 

4. 总结

DSSD针对小目标鲁棒性太差，提出了以下两个贡献：

1. 把SSD的基准网络从VGG换成了Resnet-101，并添加了残差模块，增强了特征提取能力； 
2. 使用反卷积层（deconvolution layer）增加了大量上下文信息。

因此， DSSD算法达到了更好的检测准确率，特别是对小目标也有较好的检测效果。

不足之处是时效性不高，原因：

1. 1. Resnet-101相比VGG有更多的卷积层；
   2. 增加的反卷积层带来的额外的运算；
   3. DSSD中增加了比例为1.6的default boxes，这也增加了预测时间。

DSSD 检测结果展示

 

 

声明：本篇博客并非完全原创，只是将网络上一些对于SSD算法及相关知识分析总结得十分好的文章进行整合编排。本人在此过程中也受益匪浅，特此感谢。参考博客列表或许不完整，如果带给某位博客被我引用却未注明的博主带来困扰，深感抱歉也请联系我~ 

参考资料：

SSD（single shot multibox detector）算法及Caffe代码详解

目标检测算法之SSD

ssd检测算法总结

SSD算法详解