二叉树知识

1. 二叉树的构建

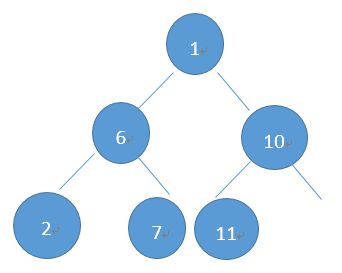
二叉树的基本构建方式为:添加一个节点，如果这是一棵空树，则将该节点作为根节点；否则按照从左到右、先左子树后右子树的顺序逐个添加节点。比如依次添加节点:1,6,10,2,7,11，则得到的二叉树为:

在这里，我们需要借助一个链表来保存节点，以实现二叉树的顺序插入，具体做法如下：
1.0 初始化一个用来保存二叉树节点的空链表；
1.1 插入一个节点，
①如果该树是一棵空树，则将该节点作为根节点，并且将该节点添加到链表中；
②如果该树不为空，取得链表第一个节点的值(注意不是链表的头节点)。如果该节点左子树为空，则将待插入节点添加到左子树，并且将左子树添加到链表；否则将待插入节点添加到右子树，将右子树添加到链表。此时，父节点的左右子树都不为空，将该父节点(即链表第一个节点)
弹出。
按照这样的顺序，我们就可以完成二叉树节点的顺序插入。

 

 

2.二叉树遍历： 

它的前序遍历顺序为：ABDGHCEIF（规则是先是根结点，再前序遍历左子树，再前序遍历右子树）

它的中序遍历顺序为：GDHBAEICF（规则是先中序遍历左子树，再是根结点，再是中序遍历右子树）

它的后序遍历顺序为：GHDBIEFCA（规则是先后序遍历左子树，再是后序遍历右子树，再是根结点）

2.2知道前序遍历和中序遍历可以算出后序，中序和后序可算出前序。但前序和后序算不出中序。

题目：已知二叉树的中根和后根序列怎么确定一棵树：

https://jingyan.baidu.com/article/295430f12112f50c7e0050c3.html

2.3平衡二叉树的概念：树上任意一节点左子树和右子树的深度之差不超过1。

2.4二叉树的度：

子树就是二叉树的分支。度就是分支的数目。
没有分叉的二叉树节点的度就是0度。如果一个节点只有一个分叉就是1度。两个分叉就是2度的子树。

2.5小根堆：

小根堆，最小堆，是一种经过排序的完全二叉树，其中任一非终端节点的数据值均不大于其左子节点和右子节点的值。

 

2.6 二叉树的定义

• 每个节点是一个自引用结构体，形式如下：

typedef int Elemtype;
 
typedef struct BiTNode{
	Elemtype data;
	struct BiTNode *lchild, *rchild;
}BiTNode, *BiTree;

2.7二叉树的插入：

• 思路：将要插入节点的键值与根节点键值比较，如果小于根节点键值，则插入根节点的左子树，如果大于根节点的键值，则插入根节点的右子树，插入子树相当于插入一个更小的树，因此可以用递归方法实现，直到找到没有子树的节点，将新节点插到其下面。注意，新节点插入后，最终只会成为叶节点。

//在给定的BST中插入结点，其数据域为element
int BSTInsert( BiTree *t, Elemtype element )
{
	if( NULL == *t ) {
		(*t) = (BiTree)malloc(sizeof(BiTNode));
		(*t)->data = element;
		(*t)->lchild = (*t)->rchild = NULL;
		return 1;
	}
 
	if( element == (*t)->data )
		return 0;
 
	if( element < (*t)->data )
		return BSTInsert( &(*t)->lchild, element );
 
	return BSTInsert( &(*t)->rchild, element );
}

//创建BST
void CreateBST( BiTree *t, Elemtype *a, int n )
{
	(*t) = NULL;
	for( int i=0; i

2.7二叉树的查找：

• 思路：与插入类似，从根节点开始，将查找的键值与根节点键值比较，若相等，则返回指向该节点的指针，若查找的键值比它大，则从根节点的右子树开始查找，若查找的键值比它小，则从根节点的左子树开始查找。可以用递归方法实现，类似于插入。这里我用迭代实现，能用迭代还是用迭代，因为递归开销比较大。

 
//中序遍历打印BST
void PrintBST( BiTree t )
{
	if( t ) {
		PrintBST( t->lchild );
		printf("%d ", t->data);
		PrintBST( t->rchild );
	}
}

 2.8 二叉树的打印，遍历

int main()
{
	int n;
	int *a;
	BiTree t;
 
	printf("请输入二叉查找树的结点数:\n");
	scanf("%d", &n);
 
	a = (int *)malloc(sizeof(int)*n);
	printf("请输入而查找树的结点:\n");
	for( int i=0; i

typedef struct file{
...
}FileInfo, *FileP;

给struct file 取个别名为FileInfo 
给struct file * 取个别名为FileP

2.9 二叉排序树又叫二叉查找树，英文名称是：Binary Sort Tree.  BST的定义就不详细说了，我用一句话概括：左 < 中 < 右。 根据这个原理，我们可以推断：BST的中序遍历必定是严格递增的。

3.0 二叉树变森林，森林变二叉树

3.1二叉树的孩子兄弟是咋回事？