偏微分方程(Partial Differential Equation I)

---

偏微分方程(Partial Differential Equation I)
偏微分方程(Partial Differential Equation II)
偏微分方程(Partial Differential Equation III)

---

参考文献：

《数学物理方程》| 季孝达
《数学物理方法》| 吴崇试
《数学物理方法》| 梁昆淼
MOOC北京大学《数学物理方法》| 吴崇试 、高春媛

偏微分方程的定解问题

偏微分方程 (Partial Differential Equations, PDE) ，是指含有多元未知函数及其若干阶偏导数的微分方程。
$$F(u,x_1,x_2,\cdots ,\frac{\partial u}{\partial x_1},\frac{\partial u}{\partial x_2},\cdots ,\frac{{\partial }^{2}u}{\partial x_1^2},\cdots )=0\text{\hspace{1em}(1.1)}$$
其中最高阶偏导数的阶称为偏微分方程的阶。

在此引入一些重要的微分算子

Hamilton 算子： $\nabla =(\frac{\partial }{\partial x},\frac{\partial }{\partial y},\frac{\partial }{\partial z})$
Laplace算子 $\Delta =\frac{{\partial }^2}{\partial x^2}+\frac{{\partial }^2}{\partial y^2}+\frac{{\partial }^2}{\partial z^2}=\nabla \cdot \nabla ={\nabla }^2$

定解问题及适定性

数学物理方程 (Equation of Mathematical Physics) ，通常指从物理学及其他各门自然科学、技术科学中产生的偏微分方程。数学物理方程有时还包括常微分方程和积分方程。本课程将着重讨论三类基本的二阶线性偏微分方程。

(1) 弦的横振动方程：未知函数 $u(x,t)$ 表示坐标 $x$ 处弦的横向位移
$$u_{tt}-a^2{u}_{xx}=f(x,t)$$
其中 $a=\sqrt{\frac{T}{\rho }},f=\frac{F}{\rho }$， $\rho$ 为弦的线密度，$T$ 为弦的切应力，$F$ 表示单位长度受到的横向力。

杆的纵振动方程：未知函数 $u(x,t)$ 表示截面相对于平衡位置 $x$ 处的纵向位移
$$u_{tt}-a^2{u}_{xx}=f(x,t)$$
其中 $a=\sqrt{\frac{E}{\rho }},f=\frac{F}{\rho }$， $\rho$ 为杆的线密度，$E$ 为杆的Young模量，$F$ 表示单位长度受到的纵向力

更一般的，三维空间的波动方程 (wave equation)是
$$u_{tt}-a^2\Delta u=f(\mathbf{r},t)\text{\hspace{1em}(1.2)}$$

(2) 热传导方程：(heat equation)未知函数 $u(\mathbf{r},t)$ 表示温度
$$u_t-a^2\Delta u=f(\mathbf{r},t)\text{\hspace{1em}(1.3)}$$
其中 $\frac{\kappa }{\rho c},\frac{F}{\rho c}$，$\kappa$ 称为热传导系数， $\rho$ 是介质的密度，$c$ 是比热容，与介质的质料有关。 $F(x,y,z,t)$ 表示介质中有热源，单位时间内在单位体积介质中产生的热量

(3) 如果热传导方程热源不随时间变化，当温度达到稳定时 $(u_t=0)$ ，温度分布满足 Poisson方程
$$\Delta u=-f/a^2\text{\hspace{1em}(1.4)}$$
如果没有热源 $(f=0)$ ，则有 Laplace方程（也称调和方程）
$$\Delta u=0\text{\hspace{1em}(1.5)}$$
静电场的电势 $u(\mathbf{r})$也满足 Poisson方程
$$\Delta u=-\rho /{ϵ}_0$$
其中 $\rho$ 为电荷密度，${ϵ}_0$ 为真空介电常数。

(4) 如果波动方程 $u(\mathbf{r},t)$ 随时间周期性变化，频率为 $\omega$，则 $u(\mathbf{r},t)=v(\mathbf{r})e^{-i\omega t}$，则 $v(\mathbf{r})$ 满足 Helmholtz 方程
$$\Delta v+k^{2}v=0\text{\hspace{1em}(1.6)}$$
其中 $k=\omega /a$ 称为波数。

通解和特解：如果多元函数 $u$ 具有偏微分方程中出现的各阶连续偏导数，并使方程 恒成立，则称此函数为方程的解，也称古典解。和常微分方程类似，称 $m$ 阶偏微分方程的含有 $m$ 个任意函数的解为通解。通解中的任意函数一旦确定便成为特解。

示例 1：求解偏微分方程
$$u_{xy}=0$$
解：先关于 $y$ 积分，得 $u_x=f(x)$，再关于 $x$ 积分，就得到通解
$$u=\int f(\xi )+f_2(\eta )=f_1(\xi )+f_2(\eta )$$
其中 $f_1,f_2$ 是任意函数。

示例 2：二维Laplace方程的通解
$$u_{xx}+u_{yy}=0$$
引入变换
$$\{\begin{array}{l}\xi =x+iy\\ \eta =x-iy\end{array}$$
根据复合函数偏导法则，进一步求得
$$\{\begin{array}{l}{u}_{xx}=u_{\xi \xi }+2u_{\xi \eta }+u_{\eta \eta }\\ u_{yy}=-(u_{\xi \xi }-2u_{\xi \eta }+u_{\eta \eta })\end{array}$$
原方程变为
$$u_{\xi \eta }=0$$
于是可求得通解
$$u(x,y)=f(x+iy)+g(x-iy)$$

定解条件：通常把反应系统内部作用导出的偏微分方程称为泛定方程。为了完全描写一个实际物理问题的确定解，我们需要在一定的制约条件，称为定解条件。偏微分方程和相应的定解条件就构成一个定解问题。常见的定解条件有以下几类：

• 初始条件：应该完全描写初始时刻（$t=0$）介质内部及边界上任意一点的状况。一般的讲，关于时间 $t$ 的 $m$ 阶偏微分方程，要给出 $m$ 个初始条件才能确定一个特解。
  对于波动方程来说，就是初始时刻的位移和速度
  $$u{|}_{t=0}=\varphi (\mathbf{r}),\frac{\partial u}{\partial t}{|}_{t=0}=\psi (\mathbf{r})$$
  对于热传导方程，只用给出初始时刻物体温度的分布状态
  $$u{|}_{t=0}=\varphi (\mathbf{r})$$
  Laplace 方程和Possion 方程都是描述稳恒状态的，与时间无关，所以不需要初始条件。

• 边界条件：边界条件形式比较多样化，要由具体问题中描述的具体状态决定。总的原则是：边界条件应该完全描写边界上各点在任意时刻的状况。
  对于弦的横振动问题，约束条件通常有以下三种

1. 如果弦的两端固定，那么边界条件就是
   $$u{|}_{x=0}=0,u{|}_{x=l}=0$$

2. 如果一端 $(x=0)$ 固定，另一端 $(x=l)$ 受位移方向的外力 $F(t)$ ，可以推导出
   $$u{|}_{x=0}=0,\frac{\partial u}{\partial x}{|}_{x=l}=\frac{1}{T}F(t)$$
   如果一端固定，另一端外力为 0，即另一端自由，则
   $$u{|}_{x=0}=0,\frac{\partial u}{\partial x}{|}_{x=l}=0$$

3. 如果外力是由弹簧提供的弹性力，即 $F(t)=-ku(l,t)$，其中 $k$ 为弹性系数，则
   $$(\frac{\partial u}{\partial x}+\sigma u){|}_{x=l}=0,\sigma =\frac{k}{T}$$

   对于热传导问题，也有类似的边界条件（以 $\partial \Omega$ 表示区域 $\Omega$ 的边界）

4. 如果边界温度分布已知，则
   $$u{|}_{\mathbf{r}\in \partial \Omega }=f(\mathbf{r},t)$$

5. 如果物体边界和周围介质绝热，则
   $$\frac{\partial u}{\partial n}{|}_{\mathbf{r}\in \partial \Omega }=0$$

6. 设周围介质的温度为 $u_1(\mathbf{r},t)$ ，物体通过边界与周围有热量交换，则
   $$(\frac{\partial u}{\partial n}+\sigma u){|}_{\mathbf{r}\in \partial \Omega }=\sigma u_1$$
   其中 $\sigma =h/k,h$表示两种物质间的热交换系数。

   常见的边界条件数学上分为三类（以 $\partial \Omega$ 表示区域 $\Omega$ 的边界，$f$ 为已知函数）

7. 第一类边界条件 (Dircichlet条件)：直接给出边界上各点未知函数 $u$ 的值
   $$u{|}_{\partial \Omega }=f(\mathbf{r},t)$$

8. 第二类边界条件 (Neu-mann条件)：给出边界外法线方向上方向导数的数值
   $$\frac{\partial u}{\partial n}{|}_{\partial \Omega }=f(\mathbf{r},t)$$

9. 第三类边界条件 (Robin条件)：给出边界上各点的函数值与外法线方向上方向导数的某一线性组合值
   $$(\frac{\partial u}{\partial n}+\sigma u){|}_{\partial \Omega }=f(\mathbf{r},t)$$

• 连接条件：从微分方程的推导知道，方程只在空间区域的内部成立，如果在区域内部出现结构上的跃变，那么在这些跃变点（线，面）上微分方程不再成立，因此需要补充上相应的条件，通常称为连接条件。
  例如，由两段不同材质组成的弦在 $x_0$ 处连接，波动方程需分段讨论，且在连接处位移和张力相等，连接条件为 $u_1(x_0,t)=u_2(x_0,t),\frac{\partial u_1}{\partial x}{|}_{x=x_0-0}=\frac{\partial u_2}{\partial x}{|}_{x=x_0+0}$

定解问题的适定性：定解问题来自于实际，它的解也应该回到实际中去。如果一个定解问题的解存在、唯一且稳定，则称该定解问题是适定的 (well-posed) 。稳定性指的是，如果定解条件的数值有细微的改变，解的数值也作细微的改变。

一阶线性偏微分方程的通解

引例：求解右行单波方程的通解
$$u_t+a{u}_x=0$$
引入变换
$$\{\begin{array}{l}\xi =x-at\\ \eta =x\end{array}$$
根据复合函数偏导法则，进一步求得
$$\{\begin{array}{l}{u}_t=-a{u}_{\xi }\\ u_x=u_{\xi }+u_{\eta }\end{array}$$
原方程变为
$$u_{\eta }=0$$
于是可求得通解
$$u(x,t)=g(x-at)$$

两个自变量一阶线性偏微分方程

先研究两自变量 $x,y$ 的一阶线性偏微分方程
$$a{u}_x+b{u}_y+cu+f=0\text{\hspace{1em}(2.1)}$$
其中 $a,b,c,f$ 都是自变量 $x,y$ 的函数。
(1) 若 $a\equiv 0,b\ne 0$ 方程改写为
$$u_y+\frac{c}{b}u+\frac{f}{b}=0$$
利用一阶线性常微分方程的求解方法可求得通解
$$u=e^{-p(x,y)}[\int e^{p(x,y)}\frac{f(x,y)}{b(x,y)}\mathrm{d}y+g(x)]$$
其中 $p(x,y)=\int \frac{c(x,y)}{b(x,y)}\mathrm{d}y,g(x)$ 是任意函数。
(2) 若 $a(x,y)b(x,y)\ne 0$ 不能直接积分求解。我们希望通过适当的自变量变换和未知函数的变换，使方程简化，并在此基础上对方程求解。

作自变量非奇异变换（可逆）
$$\{\begin{array}{l}\xi =\xi (x,y)\\ \eta =\eta (x,y)\end{array}$$
其中雅可比行列式
$$|J(\xi ,\eta )|=|\frac{\partial (\xi ,\eta )}{\partial (x,y)}|=\left|\begin{array}{cc}{\xi }_x& {\xi }_y\\ {\eta }_x& {\eta }_y\end{array}\right|\ne 0$$
以保证新变量 $\xi ,\eta$ 相互独立，利用链式法则
$$u_x=\frac{\partial u}{\partial \xi }\frac{\partial \xi }{\partial x}+\frac{\partial u}{\partial \eta }\frac{\partial \eta }{\partial x},u_y=\frac{\partial u}{\partial \xi }\frac{\partial \xi }{\partial y}+\frac{\partial u}{\partial \eta }\frac{\partial \eta }{\partial y}$$
可得到新的方程
$$A{u}_{\xi }+B{u}_{\eta }+Cu+F=0\text{\hspace{1em}(2.2)}$$
其中
$$\{\begin{array}{l}A=a{\xi }_x+b{\xi }_y\\ B=a{\eta }_x+b{\eta }_y\\ C=c,F=f\end{array}\text{\hspace{1em}(2.3)}$$
新方程仍然是线性的。
由上式看出，如果取一阶偏微分方程
$$a{z}_x+b{z}_y=0\text{\hspace{1em}(2.4)}$$
的特解作为新的自变量 $\xi$ ，此时 $A=0$，这样方程 (2.2) 得以化简为
$$B{u}_{\eta }+Cu+F=0$$
从而像第一种类型一样积分求解。
上述一阶偏微分方程方程 (2.4) 可变为常微分方程求解，首先修改为
$$a(-\frac{z_x}{z_y})-b=0$$
如果把 $z(x,y)=\text{const}$ 作为定义隐函数 $y=y(x)$ 的方程，则 $dy/dx=-z_x/z_y$，从而
$$a(x,y)\mathrm{d}y-b(x,y)\mathrm{d}x=0\text{\hspace{1em}(2.5)}$$
常微分方程 (2.5) 叫做偏微分方程 (2.1) 的特征方程，特征方程的积分曲线叫做特征线。如果求出了积分曲线簇 $z(x,y)=\text{const}$ ，再任取常数 $c$ 使得 $|J(\xi ,\eta )|\ne 0$ ，以此 $\xi ,\eta$ 作为变量代换，则一阶线性偏微分方程便可求得通解。

二阶线性偏微分方程的分类和标准式

以下研究方程的分类，并把各类方程分别化为标准型，这样以后就只需讨论标准型的解法。

两个自变量方程的分类

先研究两自变量 $x,y$ 的二阶线性偏微分方程
$$a_{11}{u}_{xx}+a_{12}{u}_{xy}+a_{22}{u}_{yy}+b_1{u}_x+b_2{u}_y+cu+f=0\text{\hspace{1em}(3.1)}$$
其中 $a_{11},a_{12},a_{22},b_1,b_2,c,f$ 都是自变量 $x,y$ 的函数。我们希望通过适当的自变量变换和未知函数的变换，使方程简化，并在此基础上对方程进行分类。

作自变量非奇异变换（可逆）
$$\{\begin{array}{l}\xi =\xi (x,y)\\ \eta =\eta (x,y)\end{array}$$
其中雅可比行列式
$$|J|=|\frac{\partial (\xi ,\eta )}{\partial (x,y)}|=\left|\begin{array}{cc}{\xi }_x& {\xi }_y\\ {\eta }_x& {\eta }_y\end{array}\right|\ne 0$$
通过代换可得到新的方程
$$A_{11}{u}_{\xi \xi }+2A_{12}{u}_{\xi \eta }+A_{22}{u}_{\eta \eta }+B_1{u}_{\xi }+B_2{u}_{\eta }+Cu+F=0\text{\hspace{1em}(3.2)}$$
其中
$$\{\begin{array}{l}{A}_{11}=a_{11}{\xi }_x^2+2a_{12}{\xi }_x{\xi }_y+a_{22}{\xi }_y^2\\ A_{12}=a_{11}{\xi }_x{\eta }_x+a_{12}({\xi }_x{\eta }_y+{\xi }_y{\eta }_x)+a_{22}{\xi }_y{\eta }_y\\ A_{22}=a_{11}{\eta }_x^2+2a_{12}{\eta }_x{\eta }_y+a_{22}{\eta }_y^2\\ B_1=a_{11}{\xi }_{xx}+2a_{12}{\xi }_{xy}+a_{22}{\xi }_{yy}+b_1{\xi }_x+b_2{\xi }_y\\ B_2=a_{11}{\eta }_{xx}+2a_{12}{\eta }_{xy}+a_{22}{\eta }_{yy}+b_1{\eta }_x+b_2{\eta }_y\\ C=c,F=f\end{array}\text{\hspace{1em}(3.3)}$$
新方程仍然是线性的。
系数 $A_{11},A_{12},A_{22}$ 可用矩阵表示为
$$\mathbf{D}=\left(\begin{array}{cc}{A}_{11}& A_{12}\\ A_{21}& A_{22}\end{array}\right)=\left(\begin{array}{cc}{\xi }_x& {\xi }_y\\ {\eta }_x& {\eta }_y\end{array}\right)\left(\begin{array}{cc}{a}_{11}& a_{12}\\ a_{21}& a_{22}\end{array}\right){\left(\begin{array}{cc}{\xi }_x& {\xi }_y\\ {\eta }_x& {\eta }_y\end{array}\right)}^T\text{\hspace{1em}(3.4)}$$
其中 $A_{12}=A_{21},a_{12}=a_{21}$

由 (3.4) 式看出，如果取一阶偏微分方程
$$a_{11}{z}_x^2+2a_{12}{z}_x{z}_y+a_{22}{z}_y^2=0$$
两个线性无关的特解作为新的自变量 $\xi ,\eta$ ，此时 $A_{11}=A_{22}=0$，这样方程 (3.2) 得以化简。
上述一阶偏微分方程可变为常微分方程求解，首先修改为
$$a_{11}(-\frac{z_x}{z_y}{)}^2-2a_{12}(-\frac{z_x}{z_y})+a_{22}=0$$
如果把 $z(x,y)=\text{const}$ 作为定义隐函数 $y=y(x)$ 的方程，则 $dy/dx=-z_x/z_y$，从而
$$a_{11}(\frac{dy}{dx}{)}^2-2a_{12}(\frac{dy}{dx})+a_{22}=0\text{\hspace{1em}(3.5)}$$
常微分方程 (3.5) 叫做偏微分方程 (3.1) 的特征方程，特征方程的积分曲线叫做特征线。
特征方程可分为两个方程
$$\frac{dy}{dx}=\frac{a_{12}\pm \sqrt{a_{12}^2-a_{11}{a}_{22}}}{a_{11}}\text{\hspace{1em}(3.6)}$$
通常根据判别式 $\Delta =a_{12}^2-a_{11}{a}_{22}$ 划分方程 (3.1) 的类型
(1) $\Delta >0$ 方程是双曲型；
(2) $\Delta =0$ 方程是抛物型；
(3) $\Delta >0$ 方程是椭圆型

由 (3.4) 矩阵的性质得到
$$A_{12}^2-A_{11}{A}_{22}=\det (\mathbf{D})=|J{|}^2(a_{12}^2-a_{11}{a}_{22})$$
这就是说，作自变量变换时，方程的类型不变。

下面就方程中 $\Delta =a_{12}^2-a_{11}{a}_{22}$ 符号的不同情况，讨论如何把方程 (3.1) 化为标准型。

• 双曲型方程：方程 (3.6) 给出两族实的特征线 $\xi (x,y)=c_1,\eta (x,y)=c_2$
  取 $\xi =\xi (x,y),\eta =\eta (x,y)$ 作为新的自变量，则 $A_{11}=A_{22}=0$，从而自变量代换后的新方程 (3.2) 成为

$$u_{\xi \eta }=-\frac{1}{2A_{12}}(B_1{u}_{\xi }+B_2{u}_{\eta }+Cu+F)$$

或者，再做自变量变换 $\xi =\alpha +\beta ,\eta =\alpha -\beta$ ，则方程化为
$$u_{\alpha \alpha }-u_{\beta \beta }=-\frac{1}{A_{12}}[(B_1+B_2)u_{\alpha }+(B_1-B_2)u_{\beta }+2Cu+2F]$$
上述两方程是双曲型方程的标准形式，弦振动方程即为标准型的双曲方程。

• 抛物型方程：特征方程只能给出一族特征线 $\xi (x,y)=c$
  取 $\xi =\xi (x,y)$ 作为新的自变量，任取一函数 $\eta =\eta (x,y)$，与 $\xi$ 线性无关。由于 $a_{12}^2-a_{11}{a}_{22}=0$，带入 (3.3) 可得
  $$\begin{gathered} A_{11}=a_{11}{\xi }_x^2+2a_{12}{\xi }_x{\xi }_y+a_{22}{\xi }_y^2=(\sqrt{a_{11}}{\xi }_x+\sqrt{a_{22}}{\xi }_y{)}^2=0 \\ {A}_{12}=a_{11}{\xi }_x{\eta }_x+a_{12}({\xi }_x{\eta }_y+{\xi }_y{\eta }_x)+a_{22}{\xi }_y{\eta }_y=(\sqrt{a_{11}}{\xi }_x+\sqrt{a_{22}}{\xi }_y)(\sqrt{a_{11}}{\eta }_x+\sqrt{a_{22}}{\eta }_y)=0 \end{gathered}$$
  从而自变量代换后的新方程成为

$$u_{\eta \eta }=-\frac{1}{2A_{22}}(B_1{u}_{\xi }+B_2{u}_{\eta }+Cu+F)$$

这是抛物型方程的标准形式，扩散方程、热传导方程都是标准形式的抛物型方程。

• 椭圆形方程：特征方程给出两族复数的特征线 $\xi (x,y)=c_1,\eta (x,y)=c_2$
  而且 $\xi =\xi (x,y),\eta =\eta (x,y)$ 共轭，对 $\xi ,\eta$ 再做自变量变换 $\xi =\alpha +i\beta ,\eta =\alpha -i\beta$ ，则新方程化为

$$u_{\alpha \alpha }+u_{\beta \beta }=-\frac{1}{A_{12}}[(B_1+B_2)u_{\alpha }+i(B_2-B_1)u_{\beta }+2Cu+2F]$$

这是椭圆型方程的标准形式，稳定温度分别、静电场方程都是椭圆型的双曲方程。

多自变量方程的分类

考虑多自变量 $x_1,x_2,\cdots ,x_n$ 的二阶线性偏微分方程
$$\sum _{j=1}^n\sum _{i=1}^n{a}_{ij}{u}_{x_i{x}_j}+\sum _{i=1}^n{b}_i{u}_{x_i}+cu+f=0\text{\hspace{1em}(3.7)}$$
做自变量的非奇异代换
$${\xi }_k={\xi }_k(x_1,x_2,\cdots ,x_n),k=1,2,\cdots ,n$$
代换的雅克比行列式
$$|J|=|\frac{\partial ({\xi }_1,{\xi }_2,\cdots ,{\xi }_n)}{\partial (x_1,x_2,\cdots ,x_n)}|\ne 0$$
通过代换可得到新的方程
$$\sum _{j=1}^n\sum _{i=1}^n{A}_{ij}{u}_{{\xi }_i{\xi }_j}+\sum _{i=1}^n{B}_i{u}_{{\xi }_i}+Cu+F=0\text{\hspace{1em}(3.8)}$$
注意到变换后的方程仍然是线性的，其中系数
$$\{\begin{array}{l}{A}_{ij}=\sum _{l=1}^n\sum _{k=1}^n{a}_{kl}\frac{\partial {\xi }_i}{\partial x_k}\frac{\partial {\xi }_j}{\partial x_l}\\ B_i=\sum _{k=1}^n\frac{\partial {\xi }_i}{\partial x_k}+\sum _{l=1}^n\sum _{k=1}^n\frac{{\partial }^2{\xi }_i}{\partial x_k\partial x_l}\end{array}$$
系数 $A_{ij}$ 可用矩阵表示为
$$(A_{ij}{)}_{n\times n}=JA{J}^T$$
其中 $A=(a_{ij}{)}_{n\times n}$ 是由方程 (3.7) 二阶偏导数的系数组成。值得注意的是系数变换公式恰恰是二次齐次式 $\sum _{j=1}^n\sum _{i=1}^n{a}_{ij}{\lambda }_i{\lambda }_j$ 系数的非奇异线性变换，二次齐次式可以通过适当的变换而对角化，即
$$(A_{ij}{)}_{n\times n}=BA{B}^T=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}(A_{11},A_{22},\cdots ,A_{nn})$$
其中 $A_{ii}\in \{-1,0,1\}$ ，根据二次齐次式对角化的惯性定律，$A_{ii}$ 为 $-1,0,1$ 的个数是一定的，设 $A_{ii}$ 中 1 的个数为 $p$ ，-1 的个数为 $q$ 。据此划分偏微分方程的类型：
(1) 当 $p=n,q=0$，椭圆型(elliptic)，标准形式是
$$\sum _{i=1}^n\frac{{\partial }^{2}u}{\partial {\xi }_i^2}+\sum _{i=1}^n{B}_i\frac{\partial u}{\partial {\xi }_i}+Cu+F=0$$
(2) 当 $p=n-1,q=0$，抛物型(parabolic)，标准形式是
$$\sum _{i=1}^{n-1}\frac{{\partial }^{2}u}{\partial {\xi }_i^2}+\sum _{i=1}^n{B}_i\frac{\partial u}{\partial {\xi }_i}+Cu+F=0$$
(3) 当 $p=1,q=n-1$，双曲型(hyperbolic)，标准形式是
$$\frac{{\partial }^{2}u}{\partial {\xi }_1^2}-\sum _{j=2}^n\frac{{\partial }^{2}u}{\partial {\xi }_j^2}+\sum _{i=1}^n{B}_i\frac{\partial u}{\partial {\xi }_i}+Cu+F=0$$
(4) 当 $p>0,q>0$，超双曲型(ultrahyperbolic)，标准形式是
$$\sum _{i=1}^p\frac{{\partial }^{2}u}{\partial {\xi }_i^2}-\sum _{j=1}^{p+q}\frac{{\partial }^{2}u}{\partial {\xi }_i^2}+\sum _{i=1}^n{B}_i\frac{\partial u}{\partial {\xi }_i}+Cu+F=0$$
常系数二阶线性偏微分方程：方程 (2.12) 中的系数 $a_{ij},b_i,c,f$ 都是常数，则方程还可以进一步化简。引入变换
$$u(\xi ,\eta )=V(\xi ,\eta )e^{\lambda \xi +\mu \eta }$$
其中 $\lambda ,\mu$ 是待定常数，根据方程的类型可选择 $\lambda ,\mu$，使一阶偏导数项或者函数项的系数为零。

波动方程的行波解

无限长弦振动初值问题：考虑两端为无限长的弦振动方程初值问题
$$\{\begin{array}{l}{u}_{tt}-a^2{u}_{xx}=0\\ u{|}_{t=0}=\varphi (x),\frac{\partial u}{\partial t}{|}_{t=0}=\psi (x)\end{array}\text{\hspace{1em}(4.1)}$$
其中 $\varphi (x),\psi (x)$ 分别表示初始位移和初始速度。
(1) 弦振动方程的通解：当 $a>0$ 为常数时，上述方程可分解为
$$(\frac{\partial }{\partial t}+a\frac{\partial u}{\partial x})(\frac{\partial }{\partial t}-a\frac{\partial }{\partial x})u=0$$
等价于两个一阶线性偏微分方程组
$$\{\begin{array}{l}\frac{\partial u}{\partial t}+a\frac{\partial u}{\partial x}=0\\ \frac{\partial u}{\partial t}-a\frac{\partial u}{\partial x}=v\end{array}$$
这两个方程有一组独立的特征线 $x+at=c_1,x-at=c_2$，引入变换 $\xi =x+at,\eta =x-at$
利用复合函数的求导法则求得 $u_{tt},u_{xx}$ 带入弦振动方程，得到新的方程
$$u_{\xi \eta }=0$$
上述方程容易求得通解
$$u=f_1(x+at)+f_2(x-at)\text{\hspace{1em}(4.2)}$$
其中 $f_1,f_2$ 是任意函数。

通解具有明确的物理意义，以 $f_2(x-at)$ 而论，改用以速度 $a$ 沿 $x$ 轴正方向移动的坐标轴 $X$，则新旧坐标和时间之间的关系为 $X=x-at,T=t$，而 $f_2(x-at)=f(X)$ 与时间 $T$ 无关。这就是说函数图像在动坐标系中保持不变，即是随着动坐标系以速度 $a$ 沿 $x$ 轴正方向移动的行波。同理， $f_1(x+at)$ 是以速度 $a$ 沿 $x$ 轴负方向移动的行波。这样，弦振动方程描述的是以速度 $a$ 沿 $x$ 轴正负两方向移动的行波。

(2) 函数 $f_1,f_2$ 由初始条件确定
将通解带入初始条件可以得到 $\{\begin{array}{l}{f}_1(x)+f_2(x)=\varphi (x)\\ a{f}_1^{\prime }(x)-a{f}_2^{\prime }(x)=\psi (x)\end{array}$ ，由此可解得
$$\begin{gathered} f_1(x)=\frac{1}{2}\varphi (x)+\frac{1}{2a}{\int }_{x_0}^x\psi (\xi )d\xi +\frac{1}{2}[f_1(x_0)-f_2(x_0)] \\ {f}_2(x)=\frac{1}{2}\varphi (x)-\frac{1}{2a}{\int }_{x_0}^x\psi (\xi )d\xi -\frac{1}{2}[f_1(x_0)-f_2(x_0)] \end{gathered}$$
将此代回 (4.2) 可得，初始问题的解
$$u(x,t)=\frac{1}{2}[\varphi (x+at)+\varphi (x-at)]+\frac{1}{2a}{\int }_{x-at}^{x+at}\psi (\xi )d\xi \text{\hspace{1em}(4.3)}$$
这个公式称为达朗贝尔(d’Alembert)公式。

(3) 物理意义示例：设初速度为零 $\psi (x)=0$，初始位移 $\varphi (x)$
如下图 $t=0$ 时刻函数图像实线所示，达朗贝尔公式给出 $u(x,t)=\frac{1}{2}\varphi (x+at)+\frac{1}{2}\varphi (x-at)$ ，即初始位移分为两半（下图虚线），分别以速度 $a$ 向左右两端移动，这两个行波的和给出各个时刻的波形（由下向上的实线）。

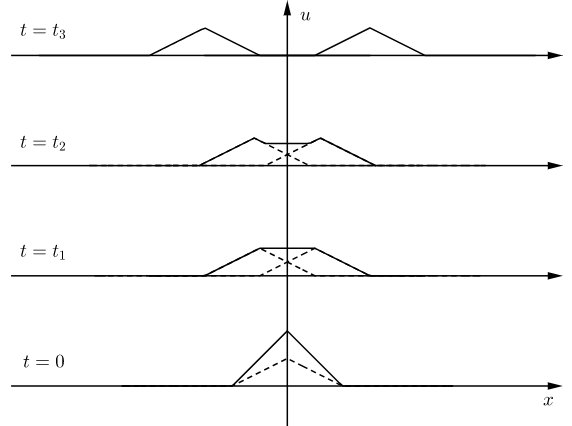
半无限弦振动定解问题 ——延拓法
(1) 端点固定弦的自由振动：定解问题为
$$\{\begin{array}{l}{u}_{tt}-a^2{u}_{xx}=0(x>0)\\ u{|}_{t=0}=\varphi (x),\frac{\partial u}{\partial t}{|}_{t=0}=\psi (x)(x⩾0)\\ u{|}_{x=0}=0\end{array}\text{\hspace{1em}(4.4)}$$
求解上述问题的基本思路是把半无限长当做无限长弦的 $x⩾0$ 的部分，然后用达朗贝尔公式求解即可。由定解条件知，振动过程 $x=0$ 处必须保持不动，由微积分知识可知，如果一个连续可微函数 $g(x)$ 在$(-\infty ,+\infty )$ 上是奇函数，则必有 $g(0)=0$ 。因此对函数 $\varphi ,\psi$ 进行奇延拓，即
$$\Phi (x)=\{\begin{array}{ll}\varphi (x)& (x⩾0)\\ -\varphi (x)& (x<0)\end{array};\Psi (x)=\{\begin{array}{ll}\psi (x)& (x⩾0)\\ -\psi (x)& (x<0)\end{array}$$
将上式带入达朗贝尔公式，可求得
$$u(x,t)=\{\begin{array}{ll}\frac{1}{2}[\varphi (x+at)+\varphi (x-at)]+\frac{1}{2a}{\int }_{x-at}^{x+at}\psi (\xi )d\xi & (t⩽\frac{x}{a})\\ \frac{1}{2}[\varphi (x+at)-\varphi (x-at)]+\frac{1}{2a}{\int }_{at-x}^{x+at}\psi (\xi )d\xi & (t>\frac{x}{a})\end{array}\text{\hspace{1em}(4.5)}$$
物理意义示例：设初速度为零 $\psi (x)=0$，初始位移 $\varphi (x)$
图中由下向上的实线描述了波形变化，右边的波分别向左右两端移动，左端奇延拓的波也分别向左右两端移动。端点固定的影响表现为反射波，反射波的相位和入射波相反，这就是半波损失。

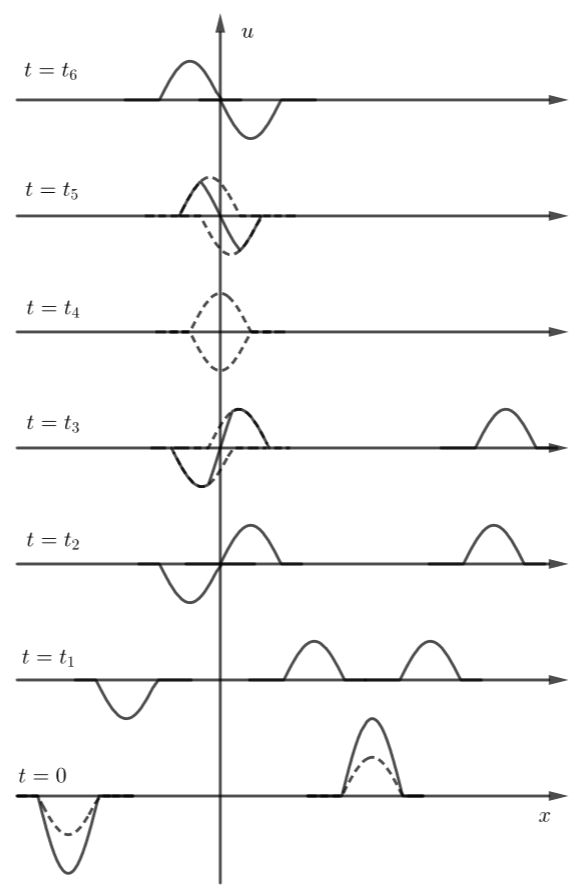
(2) 端点自由弦的自由振动：定解问题为
$$\{\begin{array}{l}{u}_{tt}-a^2{u}_{xx}=0\\ u{|}_{t=0}=\varphi (x),\frac{\partial u}{\partial t}{|}_{t=0}=\psi (x)\\ \frac{\partial u}{\partial x}{|}_{x=0}=0\end{array}(0⩽x<\infty )\text{\hspace{1em}(4.6)}$$
同样对函数进行偶延拓
$$\Phi (x)=\{\begin{array}{ll}\varphi (x)& (x⩾0)\\ \varphi (-x)& (x<0)\end{array};\Psi (x)=\{\begin{array}{ll}\psi (x)& (x⩾0)\\ \psi (-x)& (x<0)\end{array}$$
将上式带入达朗贝尔公式，可求得
$$u(x,t)=\{\begin{array}{ll}\frac{1}{2}[\varphi (x+at)+\varphi (x-at)]+\frac{1}{2a}{\int }_{x-at}^{x+at}\psi (\xi )d\xi & (t⩽\frac{x}{a})\\ \frac{1}{2}[\varphi (x+at)+\varphi (at-x)]+\frac{1}{2a}[{\int }_0^{x+at}\psi (\xi )d\xi +{\int }_0^{at-x}\psi (\xi )d\xi ]& (t>\frac{x}{a})\end{array}\text{\hspace{1em}(4.7)}$$
自由端点的影响也是一种反射波，不同的是反射波的相位和入射波相同，没有半波损失。

三维波动方程的球面波：三维波动方程在求坐标系 $(r,\theta ,\varphi )$ 下可以表示为
$$\frac{1}{a^2}\frac{{\partial }^{2}u}{\partial t^2}=\frac{1}{r^2}\frac{\partial }{\partial r}\left(r^2\frac{\partial u}{\partial r}\right)+\frac{1}{r^2\sin \theta }\frac{\partial }{\partial \theta }\left(\sin \theta \frac{\partial u}{\partial \theta }\right)+\frac{1}{r^2{\sin }^2\theta }\frac{{\partial }^{2}u}{\partial {\varphi }^2}\text{\hspace{1em}(4.8)}$$
若函数 $u$ 是球对称函数，指 $u$ 与 $\theta ,\varphi$ 无关，即 $u=u(r,t)$，方程可化为
$$\frac{{\partial }^{2}u}{\partial t^2}=a^2(\frac{{\partial }^{2}u}{\partial r^2}+\frac{2}{r}\frac{\partial u}{\partial r})$$
进一步重写为
$$\frac{{\partial }^2(ru)}{\partial t^2}=a^2\frac{{\partial }^2(ru)}{\partial r^2}$$
这时关于 $ru$ 的一维波动方程，其通解为
$$ru(r,t)=f_1(r+at)+f_2(r-at)$$
从而
$$u=\frac{f_1(r+at)+f_2(r-at)}{r}\text{\hspace{1em}(4.9)}$$
其中 $f_1,f_2$ 是任意两个二阶连续可微函数，可见，在球对称下，三维波的传播是以球心为中心，沿半径 $r$ 传播的球面波。

线性叠加原理

线性叠加原理：考虑 $n$ 个自变量（包括时间 $t$） $x_1,x_2,\cdots ,x_n$ 的二阶线性偏微分方程
$$\sum _{j=1}^n\sum _{i=1}^n{a}_{ij}{u}_{x_i{x}_j}+\sum _{i=1}^n{b}_i{u}_{x_i}+cu=f$$
其中 $a_{ij},b_i,c,f$ 是 $x_1,x_2,\cdots ,x_n$ 的已知函数，$f$ 称为方程的非齐次项。

引入微分算子
$$L=\sum _{j=1}^n\sum _{i=1}^n{a}_{ij}\frac{\partial }{\partial x_i\partial x_j}+\sum _{i=1}^n{b}_i\frac{\partial }{\partial x_i}+c$$
则可简单的表示为
$$L[u]=f$$
一般的，对任意常数 $c_1,c_2$ 和任意函数 $u_1,u_2$ ，微分算子满足性质
$$L[c_1{u}_1+c_2{u}_2]=c_{1}L[u_1]+c_{2}L[u_2]\text{\hspace{1em}(5.1)}$$
称为线性微分算子。显然，$L$ 为线性微分算子。
对于一般的线性边界条件（包括三类边界条件）也可以写成算子的形式
$$L_0[u]=(\alpha \frac{\partial u}{\partial n}+\beta u){|}_{\partial \Omega }=\varphi$$
其中 $\alpha ,\beta ,\varphi$ 是已知函数，容易证明 $L_0$ 也是线性微分算子。

叠加原理
(1) 有限叠加原理：若 $u_i$ 分别满足方程 $L[u_i]=f_i(i=1,2,\cdots ,m)$ ，则他们的线性组合 $u=\sum _{i=1}^m{c}_i{u}_i$ 满足方程
$$L[u]=\sum _{i=1}^m{c}_i{f}_i$$
(2) 级数叠加原理：若 $u_i$ 分别满足方程 L [ u i ] = f i ( i = 1 , 2 , ⋯   ) L[u_i]=f_i\quad(i=1,2,\cdots) L[u