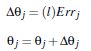机器学习日志——史上最白话的神经网络教程
先贴出BP神经网络代码如下:
class NeuralNetwork:
def __init__(self, layers, activation='tanh'):
if activation == 'logistic':
self.activation = logistic
self.activation_deriv = logistic_derivative
elif activation == 'tanh':
self.activation = tanh
self.activation_deriv = tanh_deriv
self.weights = []
for i in range(1, len(layers) - 1):
self.weights.append((2*np.random.random((layers[i - 1] + 1, layers[i] + 1))-1)*0.25)#i指当前层神经元
self.weights.append((2*np.random.random((layers[i] + 1, layers[i + 1]))-1)*0.25)
def fit(self, X, y, learning_rate=0.2, epochs=10000):
X = np.atleast_2d(X)
temp = np.ones([X.shape[0], X.shape[1]+1])
temp[:, 0:-1] = X
X = temp
y = np.array(y)
for k in range(epochs):
i = np.random.randint(X.shape[0])
a = [X[i]]
for l in range(len(self.weights)):
a.append(self.activation(np.dot(a[l], self.weights[l])))
error = y[i] - a[-1]
deltas = [error * self.activation_deriv(a[-1])]
for l in range(len(a) - 2, 0, -1):
deltas.append(deltas[-1].dot(self.weights[l].T)*self.activation_deriv(a[l]))
deltas.reverse()
for i in range(len(self.weights)):
layer = np.atleast_2d(a[i])
delta = np.atleast_2d(deltas[i])
self.weights[i] += learning_rate * layer.T.dot(delta)
def predict(self, x):
x = np.array(x)
temp = np.ones(x.shape[0]+1)
temp[0:-1] = x
a = temp
for l in range(0, len(self.weights)):
a = self.activation(np.dot(a, self.weights[l]))
return a
接下来,我将在具体的数学模型中描述上面代码的数学模型
在此之前,先介绍几个概念:
一、背景
1.1以人脑中的神经网络为启发,历史上出现过很多不同版本
1.2最著名的算法是1980年的 backpropagation(反向传播)
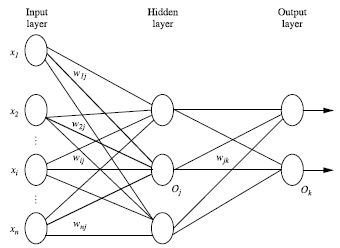
二、多层向前神经网络( Multilayer Feed- Forward Neural Network)
(1) 每层由单元(units)组成
(2) 输入层(input layer)是由训练集的实例特征向量传入
(3) 经过连接结点的权重(weight)传入下一层,一层的输出是下一层的输入
(4) 隐藏层的个数是任意的,输出层和输入层只有一个
(5) 每个单元(unit)也可以被称作神经结点,根据生物学来源定义
(6) 上图称为2层的神经网络(输入层不算)
(7) 一层中加权的求和,然后根据非线性的方程转化输出
(8) 作为多层向前神经网络,理论上,如果有足够多的隐藏层(hidden layers)和足够大的训练集,可以模拟出任何方程
三、设计一个神经网络
3.1使用神经网络训练数据之前,必须确定神经网络层数,以及每层单元个数
3.2特征向量在被传入输入层时通常被先标准化(normalize)和0和1之间(为了加强学习过程)
3.3离散型变量可以被编码成每一个输入单元对应一个特征可能赋的值
比如:特征值A可能取三个值(a0,a1,a2),可以使用三个输入单元来代表A
如果A=a0,那么代表a0的单元值就取1,其他取0
如果A=a1,那么代表a1的单元值就取1,其他取0,以此类推
例如输出值为【0,9】,那么0就是0.1,1就是0.01,2就是0.001,3就是0.003.。。。。以此类推
3.4神经网络即可以用来做分类(classification)问题,也可以解决回归(regression)问题
3.4.1对于分类问题,如果是2类,可以用一个输入单元表示(0和1分别代表2类)
如果多于两类,每一个类别用一个输出单元表示
所以输入层的单元数量通常等于类别的数量
3.4.2没有明确的规则来设计最好有多少个隐藏层
3.4.2.1根据实验测试和误差,以及准确度来实验并改进
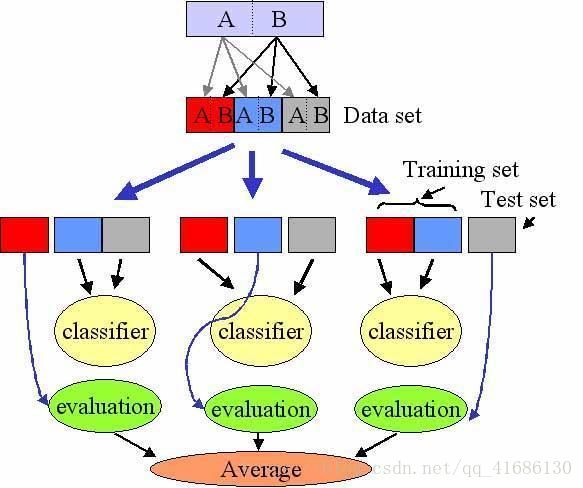
四、计算正确率——交叉验证方法
如上图所示:通过一组训练集和测试集,训练集通过训练得到模型,将测试集输入模型得到测试结果,将测试结果和测试集的真实标签进行比较,得到准确率。
在机器学习领域一个常用的方法是交叉验证方法。一组数据不分成2份,可能分为10份,
第1次:第1份作为测试集,剩余9份作为训练集;
第2次:第2份作为测试集,剩余9份作为训练集;
......
这样经过10次训练,得到10组准确率,将这10组数据求平均值得到平均准确率的结果。这里10是特例。一般意义上将数据分为k份,称该算法为K-fold cross validation,即每一次选择k份中的一份作为测试集,剩余k-1份作为训练集,重复k次,最终得到平均准确率,是一种比较科学准确的方法。
四、BP算法
通过迭代来处理训练集中的实例;
对比经过神经网络后预测值与真实值之间的差;
反方向(从输出层=>隐藏层=>输入层)来最小化误差,来更新每个连接的权重;
4.1、算法详细介绍
输入:数据集、学习率、一个多层神经网络构架;
输出:一个训练好的神经网络;
初始化权重和偏向:随机初始化在-1到1之间(或者其他),每个单元有一个偏向;
代码实现如下:
for i in range(1, len(layers) - 1):
self.weights.append((2*np.random.random((layers[i - 1] + 1, layers[i] + 1))-1)*0.25)
self.weights.append((2*np.random.random((layers[i] + 1, layers[i + 1]))-1)*0.25)对于每一个训练实例X,执行以下步骤:
1、由输入层向前传送:
结合神经网络示意图进行分析:
由输入层到隐藏层:
![]()
![]() 为每一层的偏向
为每一层的偏向
由隐藏层到输出层:
![]()
将两个公式进行总结,可以得到:
代码实现如下:
X = np.atleast_2d(X)
temp = np.ones([X.shape[0], X.shape[1]+1])
temp[:, 0:-1] = X
X = temp
y = np.array(y)
for k in range(epochs):
i = np.random.randint(X.shape[0])
a = [X[i]]
for l in range(len(self.weights)):
a.append(self.activation(np.dot(a[l], self.weights[l])))
error = y[i] - a[-1]
deltas = [error * self.activation_deriv(a[-1])]for l in range(len(a) - 2, 0, -1): deltas.append(deltas[-1].dot(self.weights[l].T)*self.activation_deriv(a[l])) deltas.reverse()
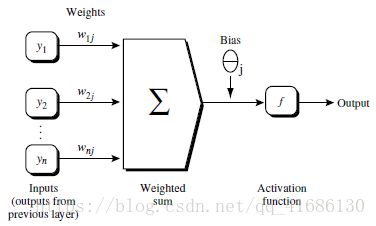
Ij为当前层单元值,Oi为上一层的单元值,wij为两层之间,连接两个单元值的权重值,sitaj为每一层的偏向值。我们要对每一层的输出进行非线性的转换,示意图如下:
当前层输出为Ij,f为非线性转化函数,又称为激活函数,有如下两种:
(1)逻辑函数
(2)双曲函数
这样就可以通过输入值正向得到每一层的输出值。
代码如下:
#定义双曲函数
def tanh(x):
return np.tanh(x)
#定义双曲函数的导数
def tanh_deriv(x):
return 1.0 - np.tanh(x)**2
def logistic(x):
return 1/(1 + np.exp(-x))
def logistic_derivative(x):
return logistic(x)*(1-logistic(x))
2、根据误差反向传送
对于输出层:其中Tk是真实值,Ok是预测值
![]()
权重更新:其中l为学习率(步进)
偏向更新:
代码实现如下:
deltas.reverse()
for i in range(len(self.weights)):
layer = np.atleast_2d(a[i])
delta = np.atleast_2d(deltas[i])
self.weights[i] += learning_rate * layer.T.dot(delta)
终止条件
1 权重的更新低于某个阈值
2 预测的错误率低于某个阈值
3 达到预设一定的循环次数
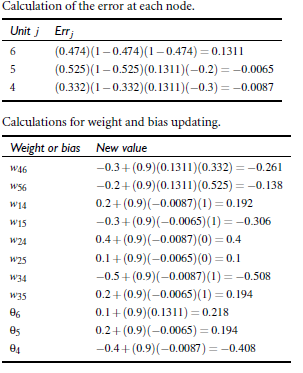
BP神经网络举例
由输入层到隐藏层:
![]()
由隐藏层到输出层:
![]()
将两个公式进行总结,可以得到:
对于输出层:![]()
对于隐藏层:![]()
五、BP神经网络的python实现详细解释
环境:python3.6
import numpy as np
#定义双曲函数
def tanh(x):
return np.tanh(x)
#定义双曲函数的导数
def tanh_deriv(x):
return 1.0 - np.tanh(x)**2
def logistic(x):
return 1/(1 + np.exp(-x))
def logistic_derivative(x):
return logistic(x)*(1-logistic(x))
#定义NeuralNetwork 神经网络算法
class NeuralNetwork:
#初始化,layes表示的是一个list,eg:[10,10,3]表示第一层10个神经元,第二层10个神经元,第三层3个神经元
def __init__(self, layers, activation='tanh'):
"""
:param layers: A list containing the number of units in each layer.
Should be at least two values
包含每个层中单元数量的列表。
应该至少有两个值(至少两层,输入层不算)
:param activation: The activation function to be used. Can be
激活函数
"logistic" or "tanh"
"""
#选择激活函数与其对应的导数
if activation == 'logistic':
self.activation = logistic
self.activation_deriv = logistic_derivative
elif activation == 'tanh':
self.activation = tanh
self.activation_deriv = tanh_deriv
self.weights = []
#循环从1开始,相当于以第二层为基准,进行权重的初始化
for i in range(1, len(layers) - 1):#len(layers)代表了神经元的层数(输入层不算)
#对当前神经节点的前驱随机赋值[-0.25,0.25]
self.weights.append((2*np.random.random((layers[i - 1] + 1, layers[i] + 1))-1)*0.25)#i指当前层神经元
#对当前神经节点的后继赋值
self.weights.append((2*np.random.random((layers[i] + 1, layers[i + 1]))-1)*0.25)
#训练函数
#X:训练集,传入的数据,通常模拟成二维矩阵,即x的每一行对应一个实例的各个特征,即行为实例个数,列为实例特征个数
#Y:分类的标记,每个实例对应的结果,即输出层单元
#learning_rate 学习率,即阶层
# epochs,表示抽样的方法对神经网络进行更新的最大次数,
def fit(self, X, y, learning_rate=0.2, epochs=10000):
X = np.atleast_2d(X) #确定X至少是二维的数据
#shape功能是查看矩阵或者数组的维数,0为行数,1为列数
temp = np.ones([X.shape[0], X.shape[1]+1]) #初始化矩阵,建立一个新矩阵[x,y],其其行数与X一样多,其列数比X多1
#:代表所有列数,0:-1代表第一列到倒数最后一列
temp[:, 0:-1] = X # 将偏置单元bias 添加到输入层
X = temp
y = np.array(y) #把list转换成array的形式
#每次随机选一个,共循环epochs次
for k in range(epochs):
#随机选取一行,对神经网络进行训练
i = np.random.randint(X.shape[0])
a = [X[i]]
#完成所有正向的更新
# 分为两步,先计算实例值与权重的乘积,再调用激活函数进行非线性转化
for l in range(len(self.weights)):
a.append(self.activation(np.dot(a[l], self.weights[l])))
#y[i]是实例值a[-1]是输出层的值
error = y[i] - a[-1]#它们之间的误差
deltas = [error * self.activation_deriv(a[-1])]
#开始反向计算误差,更新权重
for l in range(len(a) - 2, 0, -1): #我们从倒数第二层开始,倒数第一层是输出层,循环到第0层,阶层是-1
deltas.append(deltas[-1].dot(self.weights[l].T)*self.activation_deriv(a[l]))#.T表示转置,dot表示矩阵的行列式计算
#将层数颠倒
deltas.reverse()
for i in range(len(self.weights)):
#权重更新
layer = np.atleast_2d(a[i])
#偏向bias更新
delta = np.atleast_2d(deltas[i])
self.weights[i] += learning_rate * layer.T.dot(delta)
#预测函数
#参考正向输入
def predict(self, x):
x = np.array(x)
temp = np.ones(x.shape[0]+1)
temp[0:-1] = x
a = temp
for l in range(0, len(self.weights)):
#这里的话我们不需要保存每一个值,因为我们只需要输出层的值
a = self.activation(np.dot(a, self.weights[l]))
return a
举例如下:
基于NeuralNetwork的XOR(异或)规律运算
import numpy as np
from BPNeuralNetwork import NeuralNetwork
nn = NeuralNetwork([2,2,1], 'tanh')
X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
Y = np.array([0, 1, 1, 0])
nn.fit(X, Y)
for i in [[0, 0], [0, 1], [1, 0], [1,1]]:
if nn.predict(i)<0.5:
p=0
else:p=1
print(i,nn.predict(i),p)#基于NeuralNetwork的手写数字识别示例
import numpy as np
from sklearn.datasets import load_digits
from sklearn.metrics import confusion_matrix,classification_report
from sklearn.preprocessing import LabelBinarizer
from sklearn.cross_validation import train_test_split
from BPNeuralNetwork import NeuralNetwork
#加载数据集
digits = load_digits()
#加载特征向量
X = digits.data
#加载标签(输出层)
y = digits.target
#数据标准化
X -= X.min()
X /= X.max()
nn =NeuralNetwork([64,100,10],'logistic')#由于有64个像素点,所以输入层有64个神经元,输出层为0-9,
#X_train,X_test, y_train, y_test =cross_validation.train_test_split(train_data,train_target,test_size=0.3, random_state=0)
# train_data:被划分的样本特征集
# train_target:被划分的样本标签
# test_size:如果是浮点数,在0-1之间,表示样本占比;如果是整数的话就是样本的数量
# random_state:是随机数的种子
X_train, X_test, y_train, y_test = train_test_split(X, y)
# 将标签矩阵二值化,2转化为0.01,3转化为0.001
#1转化为0.1,2
labels_train = LabelBinarizer().fit_transform(y_train)
labels_test = LabelBinarizer().fit_transform(y_test)
print ("start fitting")
#开始训练
nn.fit(X_train,labels_train,epochs=3000)
predictions = []
for i in range(X_test.shape[0]):
o = nn.predict(X_test[i])
predictions.append(np.argmax(o))#选择最大概率的值
#表示预测结果,坐落在矩阵对角线的个数为预测正确的个数
print (confusion_matrix(y_test, predictions))
#precision
#recall所有真实值为3的值我们预测他为3
print (classification_report(y_test, predictions))
for l in range(len(a) - 2, 0, -1):
deltas.append(deltas[-1].dot(self.weights[l].T)*self.activation_deriv(a[l]))
for l in range(len(a) - 2, 0, -1):
deltas.append(deltas[-1].dot(self.weights[l].T)*self.activation_deriv(a[l]))
for l in range(len(a) - 2, 0, -1):
deltas.append(deltas[-1].dot(self.weights[l].T)*self.activation_deriv(a[l]))