DFS的理解和应用

目录

DFS(Depth First Search)

数塔问题

Prime Ring Problem - HDOJ 1016 / UVa 524 /（紫书P194例题7-4）

Zipper HDOJ - 1501（DFS+剪枝）

Lake Counting POJ - 2386

棋盘问题 POJ - 1321

水果消除 HNUSTOJ 

团队程序设计天梯赛--L3-015 球队“食物链”

数独挑战

---

DFS(Depth First Search)

算法竞赛中的一个重要技巧，在许多题目里，用DFS有着神奇的作用。

利用栈这种数据结构来实现（找到的第一个解不一定是最优解，只是先序遍历最早的可行解）

案例解释：走迷宫

看到哪个方向可以走就走哪个，而且你没有办法分身，所以只能慢慢试探，不撞南墙不回头。

---

数塔问题

题目描述:

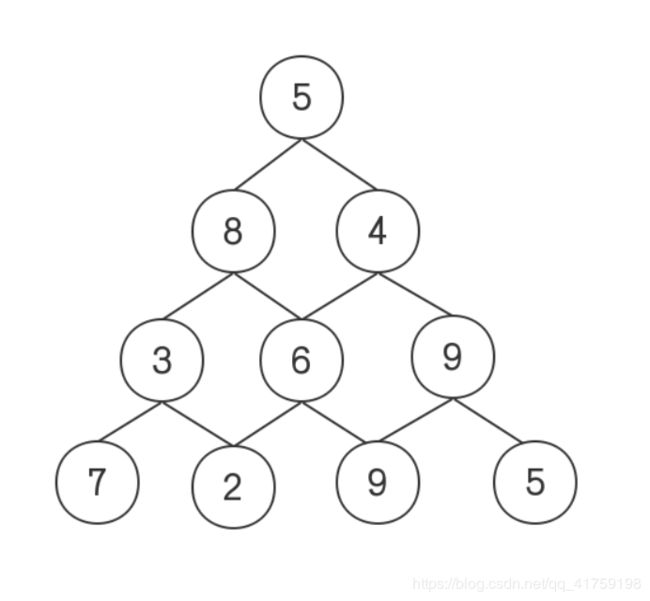
输入一个三角形塔，从三角塔顶出发向下走，每个点都有不同的权值，走到那个点就获得对应的权值，求走到塔底的时候能够获得的权值的最大值。

Sample Input

4

5

8 4

3 6 9

7 2 9 5

Sample Output

28

评论区反映这个塔不知道是怎么走的，这个塔其实就是这样的

每一个点只能走下属的两个分支的其中一个，所以，DFS的路径是5→8→6→9，5+8+6+9=28.

先来一个最普通的代码。

///数塔 1.0
#include 
#include 
#include 
#include 
#include 
#define MAX 100010
using namespace std;

int n;
int a[200][200];
int DFS(int i,int j)
{
    if(i==n)
        return a[i][j];
    int x = DFS(i+1,j);
    int y = DFS(i+1,j+1);
    return max(x,y) + a[i][j];
}

int main()
{
    while(cin>>n)
    {
        for(int i=1;i<=n;i++)
            for(int j=1;j<=i;j++)
                cin>>a[i][j];
        cout<

这个做法很直观，但是每一次都要从头开始搜，有大量的重复计算，这样非常耗时，需要优化。

可以另外加一个vis数组来存储上一次计算的结果，这样就可以节省计算时间。

///数塔 2.0
#include 
#include 
#include 
#include 
#include 
#include 
#define MAX 100010
using namespace std;

int n;
int a[200][200];
int vis[200][200];
int DFS(int i,int j)
{
    if(vis[i][j]!=-1)
        return vis[i][j];
    if(i==n)///end of this road
        vis[i][j] = a[i][j];///save the result
    else
    {
        int x = DFS(i+1,j);
        int y = DFS(i+1,j+1);
        vis[i][j] = max(x,y) + a[i][j];
    }
    return vis[i][j];
}

int main()
{
    while(cin>>n)
    {
        memset(a,0,sizeof(a));
        memset(vis,0xff,sizeof(vis));
        for(int i=1;i<=n;i++)
            for(int j=1;j<=i;j++)
                cin>>a[i][j];
        cout<

---

Prime Ring Problem - HDOJ 1016 / UVa 524 /（紫书P194例题7-4）

题目描述：输入一个正整数n，把整数1,2,3,...,n组成一个环，使得相邻两个整数之和均为素数，输出时从整数1开始逆时针排列。同一个环输出一次。（n<=16）

Sample Input

6 8

Sample Output

Case 1:
1 4 3 2 5 6
1 6 5 2 3 4

Case 2:
1 2 3 8 5 6 7 4
1 2 5 8 3 4 7 6
1 4 7 6 5 8 3 2
1 6 7 4 3 8 5 2

分析：最大的数是16，如果把所有可能结果都生成然后一个个试。。。肯定超时。

这里可以用DFS回溯，即用深度优先遍历解答树（可参考紫书的解释）

另外注意输出格式，案例之间有一个空行

///Prime Ring Problem
#include 
#include 
#include 
using namespace std;

int vis[25]={0};
int n,num[25]={0};

int is_prime(int k)///判断素数，也可以打表，那样更快
{
    int i;
    for(i=2;i<=sqrt(k);i++)
        if(k%i==0)
        return 0;
    return 1;
}
void DFS(int k)
{
    int i;
    if(k>n&&is_prime(num[n]+num[1]))///测试最后一个数和第一个数之和是否为素数
    {
        for(i=1;i>n)
    {
        if(n<1||n>19)
            break;
        printf("Case %d:\n",cnt++);
        num[1]=1;
        DFS(2);
        printf("\n");
    }
    return 0;
}

---

Zipper HDOJ - 1501（DFS+剪枝）

题目描述：给出两个字符串，问能否在不改变字符串本身顺序的情况下，拆开重组成指定字符串，输出yes/no。

Sample Input

3 
cat tree tcraete 
cat tree catrtee 
cat tree cttaree

Sample Output

Data set 1: yes 
Data set 2: yes 
Data set 3: no

 

( ˙˘˙ )没想到吧，这题居然也能用DFS。

分析：从三个串的首元素开始，遇到一串/二串与目标串匹配的字母，继续向下DFS，如果这些可以到达目标串的尾元素，那么意味着前面的都匹配成功，所以这个结果是yes，否则no。

//Zipper HDOJ 1501
#include 
#include 
using namespace std;

char a[209],b[209],c[409];
int vis[209][209]={0};
int OK=0;
void DFS(int i,int j,int k)
{
    if(vis[i][j]==1)///已经访问过，剪掉
        return;
    if(c[k]=='\0')///到指定字符串的结尾，说明之前的都匹配成功
    {
        OK=1;
        return;
    }
    if(a[i]!='\0'&&c[k]==a[i])//匹配成功
        DFS(i+1,j,k+1);
    if(b[j]!='\0'&&c[k]==b[j])//匹配成功
        DFS(i,j+1,k+1);
    vis[i][j]=1;///cut
}
int main()
{
    int n,i,j,cnt=0;
    cin>>n;
    while(n--)
    {
        OK=0;
        for(i=0;i<209;i++)///cut
            for(j=0;j<209;j++)
            vis[i][j]=0;
        scanf("%s%s%s",a,b,c);
        DFS(0,0,0);
        printf("Data set %d: %s\n",++cnt,OK?"yes":"no");
    }
    return 0;
}

---

Lake Counting POJ - 2386

题目描述：给出一张n*m的地图，求图中水洼的个数。水洼的大小不定，如果W的四周也有W，这些W组成一个大的水洼。

Sample Input

10 12
W........WW.
.WWW.....WWW
....WW...WW.
.........WW.
.........W..
..W......W..
.W.W.....WW.
W.W.W.....W.
.W.W......W.
..W.......W.

Sample Output

3

分析：找到‘W’的地，然后对其四周进行判断（DFS），并且把它附近全部变成‘.’，计算这样做的次数，即为池塘的个数。

//Lake Counting POJ2386
#include 
#include 
#include 
using namespace std;
char farm[109][109];
int n,m;

void dfs(int x,int y)
{
    farm[x][y]='.';
    int i,j;
    int tx,ty;
    for(i=-1;i<=1;i++)
    {
        for(j=-1;j<=1;j++)
        {
            tx=x+i;
            ty=y+j;
            if((tx>=0&&tx=0&&ty>n>>m)
    {
        int sum=0;
        getchar();
        for(i=0;i>farm[i][j];
            getchar();
        }
        for(i=0;i

---

棋盘问题 POJ - 1321

题目描述：给出一个n*m的棋盘，‘#’可以放棋子，求满足所有放下的棋子都不在同一行同一列的情况有多少种。（类似于八皇后问题）

Sample Input

2 1
#.
.#
4 4
...#
..#.
.#..
#...
-1 -1

Sample Output

2
1

分析：用DFS，满足条件则往下一个位置继续，如果放下的棋子已经达到要求的个数，则方法+1。

//POJ - 1321
#include 
#include 
#include 
using namespace std;
///notice that the '#' can be placed
int n,m;
int ans=0;
char map[10][10];
int vis[10];
void DFS(int x,int step)
{
    if(step == m)///found a way that work
    {
        ans++;
        return;
    }
    if(x==n)
        return;
    DFS(x+1,step);
    for(int j=0; j>n>>m)
    {
        if(n==-1 && m==-1)
            break;
        ans=0;
        memset(vis,0,sizeof(vis));
        for(int i=0; i

---

水果消除 HNUSTOJ 

题目描述：给出一个n*n的表格，表格元素是数字，相同的数字表示相同的水果，两个或以上相邻的水果可以消除，（消除之后其他水果不会改变位置），问可以消除的方案数。

Sample Input

6
1 1 2 2 2 2
1 3 2 1 1 2
2 2 2 2 2 3
3 2 3 3 1 1
2 2 2 2 3 1
2 3 2 3 2 2

Sample Output

6

分析：用DFS找某个数字周围的相同数字，如果相同就沿着这个数字向下继续找，如果相同的数字个数大于等于2，那么这样的一次搜索就是一个方案，搜索过的数字变成0，代表已经搜索过，最终输出方案数。

///水果消除 HNUSTOJ
#include 
#include 
using namespace std;
///notice that the '#' can be placed while '.' not
int map[1000][1000];
int dir[4][2]= {{1,0},{-1,0},{0,1},{0,-1}};
int n;
int num;
void DFS(int x,int y,int k)
{
    map[x][y]=0;
    int i;
    int tx,ty;
    for(i=0;i<4;i++)
    {
        tx=x+dir[i][0];
        ty=y+dir[i][1];
        if(tx>=0 && tx=0 && ty>n)
    {
        int sum=0;
        for(int i=0;i1)
                         sum++;
                }
        printf("%d\n",sum);
    }
    return 0;
}

---

团队程序设计天梯赛--L3-015 球队“食物链”

题目链接

某国的足球联赛中有N支参赛球队，编号从1至N。联赛采用主客场双循环赛制，参赛球队两两之间在双方主场各赛一场。

联赛战罢，结果已经尘埃落定。此时，联赛主席突发奇想，希望从中找出一条包含所有球队的“食物链”，来说明联赛的精彩程度。“食物链”为一个1至N的排列{ T​1​​ T​2​​ ⋯ T​N​​ }，满足：球队T​1​​战胜过球队T​2​​，球队T​2​​战胜过球队T​3​​，⋯，球队T​(N−1)​​战胜过球队T​N​​，球队T​N​​战胜过球队T​1​​。

现在主席请你从联赛结果中找出“食物链”。若存在多条“食物链”，请找出字典序最小的。

注：排列{ a​1​​ a​2​​ ⋯ a​N​​}在字典序上小于排列{ b​1​​ b​2​​ ⋯ b​N​​ }，当且仅当存在整数K（1≤K≤N），满足：a​K​​

输入格式：

输入第一行给出一个整数N（2≤N≤20），为参赛球队数。随后N行，每行N个字符，给出了N×N的联赛结果表，其中第i行第j列的字符为球队i在主场对阵球队j的比赛结果：W表示球队i战胜球队j，L表示球队i负于球队j，D表示两队打平，-表示无效（当i=j时）。输入中无多余空格。

输出格式：

按题目要求找到“食物链”T​1​​ T​2​​ ⋯ T​N​​，将这N个数依次输出在一行上，数字间以1个空格分隔，行的首尾不得有多余空格。若不存在“食物链”，输出“No Solution”。

输入样例1：

5
-LWDW
W-LDW
WW-LW
DWW-W
DDLW-

输出样例1：

1 3 5 4 2

输入样例2：

5
-WDDW
D-DWL
DD-DW
DDW-D
DDDD-

输出样例2：

No Solution

分析：DFS+剪枝，详细见代码注释~

///球队食物链
#include

using namespace std;
const int maxn = 30;
char ar[maxn][maxn];
int N;
int  w[maxn][maxn];
bool vis[maxn];
int  ans[maxn];
bool dfs(int i,int num)
{
    if(num == N && w[i][0])///都走到这里了，答案肯定已经确定了
    {
        for(int k = 0; k < N; ++k)///输出结果
        {
            if(k)
                cout<<' ';
            cout<= N)///怎么都不能形成环
        return false;



    for(int j = 1; j < N; ++j)
    {
        if(!vis[j]&&w[i][j])
        {
            ans[num] = j;
            vis[j] = 1;
            if(dfs(j,num+1))
                return true;
            vis[j] = false;
        }
    }
    return false;
}

int main()
{
    ios::sync_with_stdio(false);
    cin>>N;
    for(int i = 0; i < N; ++i)
        cin>>ar[i];
    for(int i = 0; i < N; ++i)
    {
        for(int j = 0; j < N; ++j)
        {
            if(i == j)
                continue;
            if(ar[i][j] =='W')
                w[i][j] = 1;
            else if(ar[i][j] == 'L')
                w[j][i] = 1;
        }
    }
    vis[0] = 1;
    ans[0] = 0;
    if(!dfs(0,1))
        printf("No Solution");
    return  0;
}

---

数独挑战

题目链接

题解

---

=======最后更新时间：2019.07.09=======

=======遇到好的题目会回来继续更新======

===如果各位大牛牪犇路过发现问题欢迎反映  (｢･ω･)｢嘿===

附上另外一篇：BFS的理解和应用，欢迎前去围观~