算法进阶---理解树形背包问题

在网上看了好多树形背包问题的讲解博文，感觉好多都是相互复制，并没有把问题讲清楚，理解起来十分费力。因而，我想用这篇博文将我的理解记录下来，与大家分享。写的不好的地方也请大家多多指教！

---

1. 问题定义

给定$N$件物品，第i件物品的重量为$w[i]$，价值为$v[i]$，且物品之间存在依赖关系，即如果物品$i$依赖于物品$j$，则必须在选取了$j$后才能选取$i$（从树的角度描述就是：$j$是$i$的父节点，要选择子节点$i$的前提是父节点$j$已经被选取 ）。给你一个容量为$C$的背包，求装入背包中的物品的最大总价值。

---

2. 首先考虑特殊情况$w[i]=1,\forall i$

首先，我们先考虑这个问题的特殊情况，也就是所有物品的重量都为1的情况。这时，状态转移方程为：

$dp[i][j][k]=max(dp[i][j][k],dp[i][j-1][k-m]+dp[i的第j个孩子u][u的子节点总数][m])$
$dp[i][j][k]$表示的是以节点$i$为根，只考虑$i$的前$j$个子节点，且背包重量为$k$时所能获得的最大总价值。

从这个状态转移方程我们可以看出想要求出$dp[i][j][k]$，我们需要两个信息：（1）$dp[i][j-1][x]$；（2）$dp[i的第j个子节点u][u的子节点数目][y]$。

所以，对这个状态转移方程的直观理解就是：如果我知道了从$i$的前$j-1$个节点取总重量为$x$的物品时可以获取的最大值（也就是$dp[i][j-1][x]$）,同时知道了从$i$的第$j$个节点$u$取总重量为$y$的物品时可以获取的最大值（也就是$dp[u][u的子节点数目][y]$），那么我就可以求出从$i$的前$j$个节点取总重量为$k$的物品时可以获取的最大值，求的方式就是将总重量$k$在$i$的前$j-1$个子节点（对应$dp[i][j-1][k-m]$）和新加入的第$j$个节点$u$（对应$dp[i的第j个孩子u][u的子节点总数][m]$）之间分配，并且求出所有分配情况中的最大值。所以，可以看到dp数组的第三维下标分别为$k-m$和$m$，和正好为$k$。

理解了状态转移方程以后，我们再来分析一下解决问题需要的两个信息：信息（1）dp[i][j-1][x]说明我们在求$dp[i][j][k]$时只要用到$dp[i][j-1][x]$，也就是说，$dp[i][j]$只从$dp[i][j-1]$转移而来，所以，我们可以将dp的第二维去掉从而将dp从三维降为二维从而节约空间。简化后的状态转移方程如下：

$dp[i][k]=max(dp[i][k],dp[i][k-m]+dp[i的第j个孩子u][m])$

信息（2）dp[i的第j个子节点u][u的子节点数目][y]说明我们在求$dp[i][j][k]$时，需要知道从$i$的第$j$个子节点$u$取出总重量为$y$的物品时的最大值。由于dp的第二维表示的是仅考虑前$j$个子节点时的结果，而信息(2)的第二维是$u$的子节点数目，也就说明$dp[u][u的子节点数目][y]$包含的结果是将$u$的所有子节点都考虑到了的结果，所以，这个dp数组包含的实际就是以$u$为根节点的最终结果。这里就暗示了DFS的思路，即想要求$i$的结果$dp[i][j][k]$，必须先求出$i$的子节点$u$的结果！（DFS的过程会在后面的例题中体现，这里只需要理解为什么需要DFS即可。）

到这我想大家应该能模模糊糊理解树形背包问题的解题思路了，接下来我们看一些例题来实战一下。

---

3. 例题一：$w[i]=1,\forall i$

此题来自HDU - 1561: The more, The Better

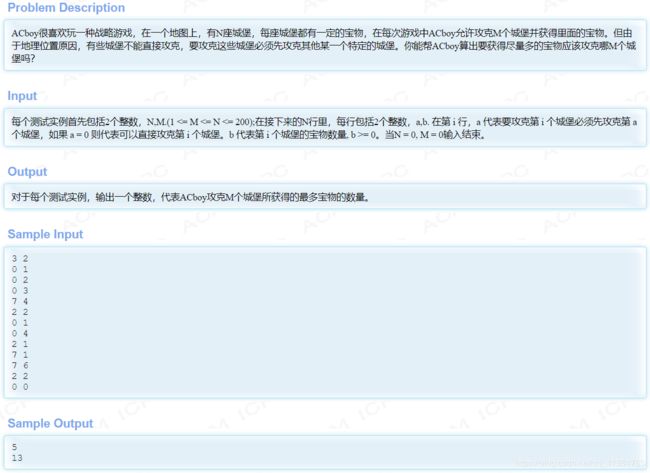
下面直接给出带注释的AC代码，可以结合之前的分析来看，应该不难理解！

#include 
#include 
#include 
using namespace std;

const int MAX = 205;
int n, m, v[MAX];
vector son[MAX];
int dp[MAX][MAX];

void dfs(int cur)
{
    dp[cur][1] = v[cur];
    int len = son[cur].size(); //看cur有几个子节点
    for (int i = 0; i < len; i++) //挨个遍历cur的每个子节点
    { 
        int son_index = son[cur][i];
        dfs(son_index); //先dfs得到son_index的结果dp[son_index]
        for (int j = m + 1; j >= 2; j--) // 这里开始求dp[cur][j]
        { 
            for (int k = 1; k < j; k++) // k用于从j中分出一部分重量给本轮的子节点son_index
            {                                                                    
                dp[cur][j] = max(dp[cur][j], dp[cur][j - k] + dp[son_index][k]); 
            }
        }
    }
}

void init()
{
    memset(v, 0, sizeof(v));
    memset(dp, 0, sizeof(dp));
    for (int i = 0; i <= n; i++)
        son[i].clear();
}

int main()
{
    int i, u;
    while (scanf("%d%d", &n, &m), n || m)
    {
        init();
        for (i = 1; i <= n; i++)
        {
            scanf("%d%d", &u, &v[i]);
            son[u].push_back(i);
        }
        dfs(0);
        printf("%d\n", dp[0][m + 1]);
    }
    return 0;
}

---

4. 例题二：$w[i]=any$

现在让我们回到更一般的情况，假设不同的物品有不同的重量，且不都为1.
此题来自HDU - 1011: Starship Troopers


同样直接放有注释的AC代码，dp的过程其实和所有物品重量为1时差不多，正好可以用于读者检验自己是否真正理解了树形背包问题的核心思想。

#include 
#include 
#include 
#include 
#include 
using namespace std;

const int MAX = 101;
int n, m;
int dp[MAX][MAX];
struct Room
{
    int bugs, possibility;
    vector next;
} rooms[MAX];

void init()
{
    memset(dp, 0, sizeof(dp));
    for (int i = 1; i <= n; i++)
        rooms[i].next.clear();
}

void dfs(int cur, int father, int trooper)
{
    for (int i = rooms[cur].bugs; i <= trooper; i++)
        dp[cur][i] = rooms[cur].possibility;
    if (trooper <= rooms[cur].bugs)
        return; // 如果剩余的士兵已经不够了，直接返回
    int len = rooms[cur].next.size(); // 看cur有几个子节点
    for (int i = 0; i < len; i++) // 挨个遍历子节点
    {
        int son = rooms[cur].next[i];
        if (son == father)
            continue; // 防止从子节点遍历回父节点
        dfs(son, cur, trooper - rooms[cur].bugs);
        for (int j = trooper; j > rooms[cur].bugs; j--) // j>rooms[cur].bugs时才有意义
        {                                  
            int upper_bound = j - rooms[cur].bugs; // 对于任意j，可以被son分走的部分（即k）的上界是j-rooms[cur].bugs
            for (int k = 1; k <= upper_bound; k++)
                dp[cur][j] = max(dp[cur][j], dp[cur][j - k] + dp[son][k]);
        }
    }
}

int main()
{
    int i, b, u, v;
    while (scanf("%d%d", &n, &m), (~n))
    {
        init();
        for (i = 1; i <= n; i++)
        {
            scanf("%d%d", &b, &rooms[i].possibility);
            rooms[i].bugs = ceil((double)b / 20);
        }
        for (i = 1; i < n; i++)
        {
            scanf("%d%d", &u, &v);
            rooms[u].next.push_back(v);
            rooms[v].next.push_back(u);
        }
        if (n && m)
        {
            dfs(1, 0, m);
            printf("%d\n", dp[1][m]);
        }
        else
            printf("0\n");
    }
    return 0;
}

---

5. 写在最后：泛化物品

好多文章在讲树形背包问题时，上来就给出泛化物品的定义，直接就给我整晕了。其实，不了解泛化物品的定义几乎不影响对树形背包问题的理解，所以，我把他放到最后来讲。

泛化物品定义：考虑这样的物品，它没有固定的重量和价值，它的价值随着分配给它的重量的变化而变化。抽象成数学模型是一个定义域为$[0,W]$中整数的函数$V[w]$，对于每个在定义域中的$w$，对应一个价值$V[w]$。

泛化物品的和：将两个泛化物品合并成为1个物品，方法是枚举重量分配的方式，即：

$V[w]=max(V1(i)+V2(w-i))，其中0<=i<=w$

那么泛化物品和树形背包问题有啥关系呢？仔细看一下状态转移方程，你会发现，其实dp的过程就是算泛化物品的和的过程。为了对比方便，这里再列一下状态转移方程：

$dp[i][k]=max(dp[i][k],dp[i][k-m]+dp[i的第j个孩子u][m])$

---

参考资料

• 树形DP进阶之背包问题。https://blog.csdn.net/zhangmh93425/article/details/45269411
• 【HDU - 1561】The more, The Better（树形背包，dp，依赖背包问题与空间优化，tricks）。https://blog.nowcoder.net/n/97a3b7a6ab994300a69076080f694759
• 动态规划之树形依赖的背包问题。http://littleroach110.net/2017/03/14/Tree-Rely-Knapsack.html
• 有树形依赖的背包问题。https://www.cnblogs.com/GXZC/archive/2013/01/13/2858649.html