leetcode每日一题05.23——76.最小覆盖子串 及 滑动窗口算法框架

滑动窗口？

对于字符串和数组的子序列(子串是一个特殊的子序列)问题,我们都可以使用暴力解法遍历所有的子串,在子串中寻找是否符合题目要求的。这种遍历所有子串的算法也是滑动算法的一种,是不加约束的，没有约束就会导致很多不必要的计算,所以对于能暴力滑动窗口解决子串类的题目。我们都可以考虑通过添加约束来减少时间复杂度，来达到想要的结果。

什么时候用滑动窗口算法？

我个人认为,解决字符串和数组的子串或子序列问题，都可以使用滑动窗口算法，且尽量的加上约束。

滑动窗口算法框架

下面举出一个滑动窗口算法的框架模板，两处...分别表示窗口右移和左移时候的操作,有很多情况该两处操作是对称的。

滑动窗口的核心是左右指针的滑动。右指针的滑动是为了寻找一个可行解,左指针的滑动是为了寻找一个最优解.左指针每滑动一次,我们就需要用一个值local_min记录该解一次.local_min保留的是从开始到目前位置的局部最优解.当遍历了整个子串之后,我们所剩下的local_min就是整体最优解了。

• s表示源串,t表示子串.
• need表示题目要求子串所应该满足的条件。
• window表示目前窗口所包含子串里面的信息。
• valid表示window当中已经满足need要求的字符个数 的数量。

/* 滑动窗口算法框架     来源Leetcode  */
void slidingWindow(string s, string t) {
    unordered_map need, window;
    for (char c : t) need[c]++;
    int local_min;
    int left = 0, right = 0;
    int valid = 0; 
    while (right < s.size()) {
        // c 是将移入窗口的字符
        char c = s[right];
        // 右移窗口
        right++;
        // 进行窗口内数据的一系列更新
        ...

        /*** debug 输出的位置 ***/
        printf("window: [%d, %d)\n", left, right);
        /********************/
        
        // 判断左侧窗口是否要收缩
        while (window needs shrink) {
        	
            // d 是将移出窗口的字符
            char d = s[left];
            // 左移窗口
            left++;
            //记录该解.
        	local_min=left;
            // 进行窗口内数据的一系列更新
            ...
        }
    }
}

作者：labuladong
链接：https://leetcode-cn.com/problems/minimum-window-substring/solution/hua-dong-chuang-kou-suan-fa-tong-yong-si-xiang-by-/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

例题

例题一 leetcode 3.无重复字符的最长字串

无重复字符的最长字串

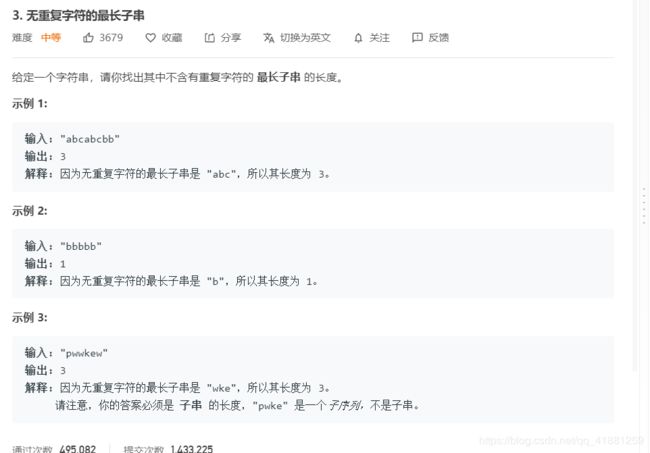
解题思路：
首先分析右指针和左指针滑动的时候我们要做的事情：
在此题中,滑动窗口应该是不含有重复字符的子串.
在该问题当中,右指针右移就是寻找可行解,同时也是寻找最优解的过程。(因为题目要求最长)。

我们用window来表示当前窗口各个字符的数目。

1. 纳入right指向的字符,之后判断窗口中是否存在重复字符
2. 不存在重复字符,该窗口的解是一个可行解.同时也是当前的最优解。
3. 存在重复字符，需要将左端窗口收缩,直至不存在重复字符为止，无重复字符的窗口也是一个可行解，记录该解。

代码:

//滑动窗口的关键是找到可行解,在可行解中寻找最优解的过程。
//对本次题来说,right指向了当前窗口最后一个元素的下一个位置.
//将right位置的字符纳入窗口,判断窗口中是否存在相同元素.无重复的话这就是一个可行解，记录长度。
//存在重复的话,就开始移动left.直至没有重复为止，记录长度。
class Solution {
public:
    int lengthOfLongestSubstring(string s) {
        if(s.length()==0){
            return 0;
        }
        map window;
        int left=0,right=0;
        int len=0;

        while(right1){
                char d=s[left];
                window[d]--;
                left++;  
            }
            len=max(len,right-left);
        }
        return len;
    }
};

例题二 leetocde567.字符串的排列

字符串的排列

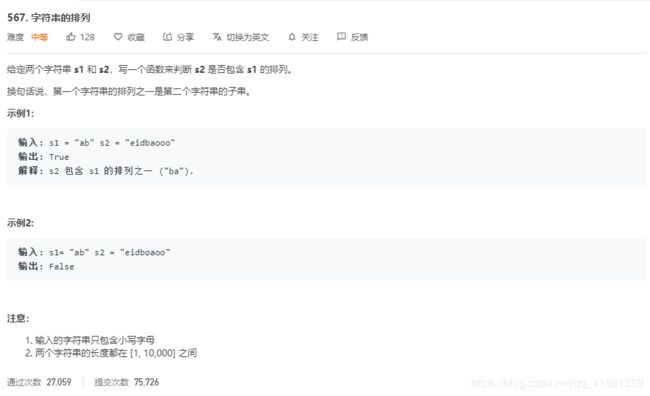
这道题第一眼看起来好像需要求s1的所有排列,然后依次判断s2中是否包含该排列。
但是有更好的思路，就是求s是否存在一个子串，该子串包含t中的所有字符且不包含其他字符？
这种子串类问题,我们要下意识的考虑到滑动窗口算法。

算法思路：移入元素时考虑是否当前元素是否满足need的要求,满足的话就valid++,如果窗口长度大于等于s1长度，就要收缩滑动窗口。收缩的时候判断是否产生了我们要求的解。然后记录左端窗口元素.将其移出滑动窗口即可，最后如果都没有找到解,就返回false.
代码

//判断S是否存在一个子串,使得该子串只包含t中的所有字符而不包含其他字符.

class Solution {
public:
    bool checkInclusion(string s1, string s2) {
        map need,window;
        for(int i=0;i=s1.length()){
                //收缩的时候可能产生解。
                if(valid==need.size()) return true;
                char d=s2[left];

                left++;
                if(need.find(d)!=need.end()){
                    if(window[d]==need[d])
                        valid--;
                    window[d]--;
                }
            }
        }
        return false;
    }
};

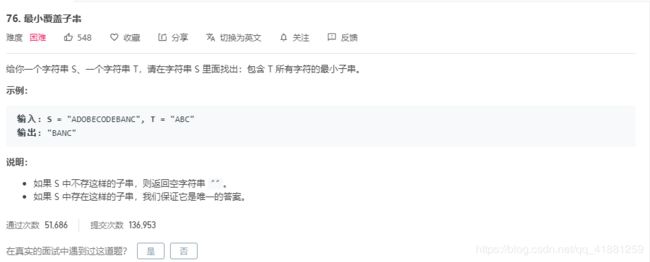
例题3 leetcode438找到字符串中所有字母异位词

这题和例题二是一样的套路，问在s串的所有的子串当中,找到只包含t中所有字符串的子串。
代码

//注意,本身也是本身的异位词.

//在s中寻找子串,要求该子串

class Solution {
public:
    vector findAnagrams(string s, string p) {
        map need,window;
        for(int i=0;i res;
        int valid=0;
        while(right=p.length()){
                if(valid==need.size()) res.push_back(left);
                char d=s[left];
                left++;
                if(need.find(d)!=need.end()){
                    if(need[d]==window[d])
                        valid--;
                    window[d]--;
                }
            }
        }
        return res;
    }
};

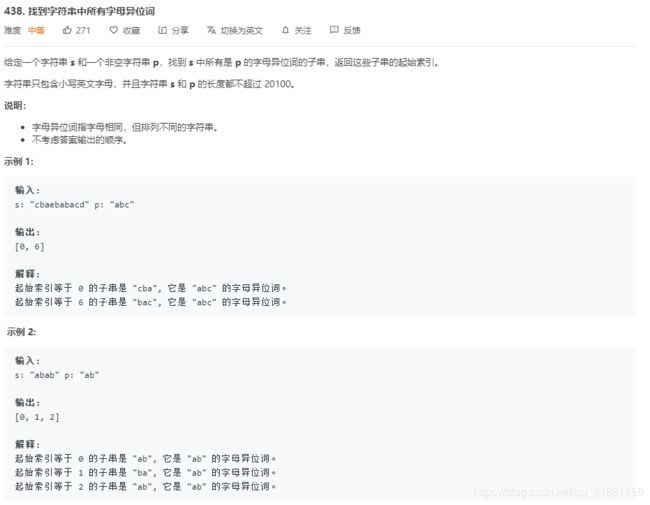
例题4 leetcode76.最小覆盖子串

这题是要求一个S的子串,使得该子串包含T中的所有字符，且该子串的长度最小.
解题思路：我们先拉长滑动窗口求出一个可以满足包含T的所有字符的解,然后缩短窗口求出一个最优解。
代码

//我们要求j-i的最小值,并输出string[i]->string[j].

//dp不会.采用题解进行双指针解决.  
//整体思路:先找到可行解,再优化可行解.直至最后。
//怎么找可行解? 右指针右移直到左右指针的窗口包含了t字符串中的所有字符.这是可行解,记录该解.
//怎么优化可行解？ 找到可行解之后,将左指针右移.直到不包含t字符串中的所有字符为止.且每左移一次,就将要返回的答案更新一次.
//当右指针到了末尾的时候,当前的最优解就是整体的最优解了.
class Solution {
public:
    string minWindow(string s, string t) {

        map need,window; //need表示需要的字符个数, widow表示窗口已经有的字符个数.
        for(int i=0;i

总结

这篇文章写了滑动窗口算法框架。当我们想要解决字符串的子串匹配问题时候，我们要多考虑一下滑动窗口算法~！

再附上一个leetcode的滑动窗口算法链接,总结的挺好的.之后也可以看一下~
将滑动窗口算法变成默写题