图形学复习
文章目录
- charpter1
- 图形学的基本应用(C1,E33)
- 光栅图形,相关定义(如像素、真彩色、帧缓存等)与计算(C4,E35)
- 图形学的历史(CG01)
- 人类视觉系统(C16)(如光谱(C13)、颜色模型(C49, E98))
- 三维图形的处理流程(如顶点、裁剪、光栅化、片元等)(C25,E65)
- chapter2
- OpenGL 与 WebGL简介
- OpenGL 与WebGL函数的使用
- opengl基本函数分类
- 指定OpenGL窗口的显示模式的函数是什么?并给出互斥参数的比较分析。
- WebGL的绘制流水线
- 颜色索引(C51)
- chapter3
- 双缓存 C75
- 物理设备(C7)(多种类型)与逻辑设备(C9)(6种基本类型)
- 三种基本的输入模式(请求、采样、事件)C10
- GLUT的基本回调函数(显示、鼠标、形变、键盘、空闲等)C57,72
- chapter4
- 标量、向量、点的概念 C82
- 仿射空间
- 点积和叉积(图形学意义)C88
- 维数、基、坐标系与标架 C91
- Homogeneous Coordinates C95
- 三种基本变换:平移、旋转、缩放(2D与3D)C111
- 组合变换(顺序问题)C117
- 多边形网格、多面体、欧拉公式(CG14) 、四元数(C132,CG13)
- chapter5
- 平面几何投影的分类(平行与透视)C139
- 不同领域的经典视图 C139
- 灭点的概念 C142
- 建立观察标架 C143、CG16
- 照相机标架的定位 C144
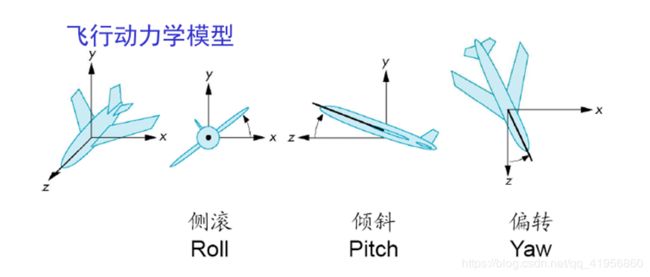
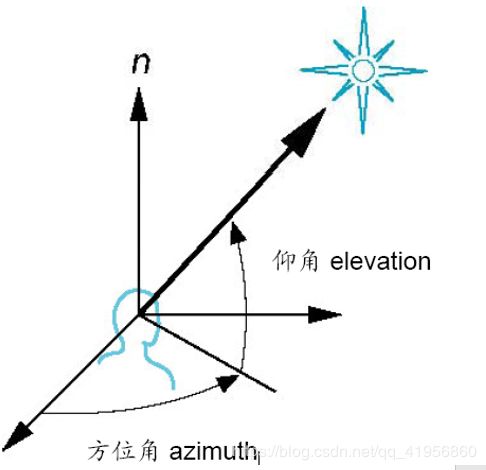
- 其它视图API(如Yaw、Pitch、Roll,方位角、仰角)C150
- 投影规范化 C153 C162 CG17
- chapter 6
- Phong光照模型三个分量:环境光、漫反射光、镜面反射光 C186、 CG18
- 反射系数与高光系数 C188
- 中值向量与改进Phong光照模型 C189、CG19
- Gouraud模型与Phong模型的明暗处理对比 C193、CG19
- 均匀着色
- 平滑着色
- Phong着色
- Chapter 8
- 面向图像与面向对象的方法C214、CG21
- 隐藏面消除 的对象空间和图像空间消隐算法 C235
- 线段的裁剪:Cohen-Sutherland法(区域编码)、Liang-Barsky法(参数顺序) C218、CG21
- 多边形的裁剪:Sutherland-Hodgeman算法(裁剪与重构的4种情况)C222、CG22
- 文本裁剪的方法(字符串、字符、矢量)C225、CG22
- 画家算法(C241)与深度缓存算法(C238)(Z-Buffer)CG22
- 线段的扫描转换:DDA、Bresenham(中点画线算法)C229、CG23
- 多边形的扫描转换:ET、AET、奇偶规则(C232)、特殊情况处理(C234) CG23
- 走样(若干现象)与反走样(两种方法)C243、CG23
- chapter11
- 曲线曲面的表达方式:显示、隐式、参数 C355
- 三次曲线: Hermite(C363)、Bezier(C366)、B-spline (C368)
- chapter12
- 光线跟踪(Ray tracing)概念 C391 CG40
- 辐射度(Radiosity)概念 C398 CG41
说明:标题后面括号内容表示页码,
如 C1表示中文版第1页,E33表示英文版第33页, CG09-1表示PPTCG09第1页
charpter1
图形学的基本应用(C1,E33)
- Display of information
- Design
- Simulation and animation
VR & AR
• 虚拟现实(VR),也称灵境技术或人工环境。综合利用计算机图形系统和各种现实及控制等接口设备,在计算机上生成的、可交互的三维环境中提供沉浸感觉的技术。其中,计算机生成的、可交互的三维环境成为虚拟环境(即Virtual Environment,简称VE)。
• 增强现实(AR,Augmented Reality),也称之为混合现实。它通过电脑技术,将虚拟的信息应用到真实世界,真实的环境和虚拟的物体实时地叠加到了同一个画面或空间同时存在。增强现实不仅展现了真实世界的信息,而且将虚拟的信息同时显示出来,两种信息相互补充、叠加。
- User interfaces
光栅图形,相关定义(如像素、真彩色、帧缓存等)与计算(C4,E35)
-
Raster 光栅
Array of pixels -
光栅图形:光栅图也叫做位图、点阵图、像素图,简单的说,就是最小单位由像素构成的图,只有点的信息,缩放时会失真。每个像素有自己的颜色,类似电脑里的图片都是像素图,把它放很大就会看到点变成小色块了。
-
Pixel 象素Picture element
-
Resolution 分辨率Number of pixels in frame buffer
-
Frame Buffer 帧缓存
Memory where pixels stored由像素组成的二维数组,每一个存储单元对应屏幕上的一个像素,整个帧缓存对应一帧图像。其中的分辨率表示像素数,深度(或精度)表示每个像素所用的比特数,深度为n bit的帧缓存可以表示2n种颜色。 -
true-color 真彩色,RGB每种原色分配8bit,从而每个像素24bit
-
Depth 深度 of Frame Buffer
Number of bits that are used for each pixel (ex. 8-bit-depth 28(=256) colors, 24 or more bits per pixel RGB-color) -
Rasterization 光栅化 (Scan Conversion扫描转换)
Converting of geometric entities (such as lines, circles, and polygons) to pixel assignment in frame buffer 从几何实体到帧缓存中像素的颜色和位置的转化图形与图像:
图形是矢量图(Vector Drawn),它是根据几何特性来绘制的。图形的元素是一些点、直线、弧线等。矢量图常用于框架结构的图形处理,应用非常广泛,如计算机辅助设计(CAD)系统中常用矢量图来描述十分复杂的几何图形,适用于直线以及其它可以用角度、坐标和距离来表示的图。图形任意放大或者缩小后,清晰依旧。
图像是位图(Bitmap), 它所包含的信息是用像素来度量的。就像细胞是组成人体的最小单元一样,像素是组成一幅图像的最小单元。对图像的描述与分辨率和色彩的颜色种数有关,分辨率与色彩位数越高,占用存储空间就越大,图像越清晰。
图形是人们根据客观事物制作生成的,它不是客观存在的;图像是可以直接通过照相、扫描、摄像得到,也可以通过绘制得到。
图形学的历史(CG01)
人类视觉系统(C16)(如光谱(C13)、颜色模型(C49, E98))
- RGB:加色模型(additive color model)
- CMY(Cyan, Megenta, Yellow) : 减色模型(subtractive color model),C,M,Y分别是R,G,B的互补色(complementary color), 即白色减去R就是C。应用于商业打印和绘图中。
- color gamut 色域, 一个设备可以生成的颜色集
- color solid 颜色立方体
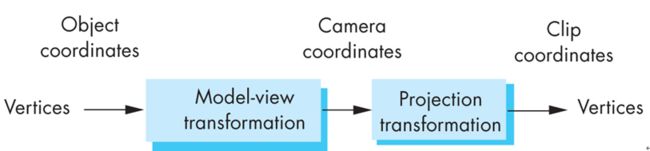
三维图形的处理流程(如顶点、裁剪、光栅化、片元等)(C25,E65)
- Vertex Processing
- 顶点包含了拓扑信息(Topology):邻接和次序关系。几何信息(Geometry): 点的位置坐标
- The two major functions of this block are to carry out coordinate transformation and to compute a color for each vertex.
Projection:
- Perspective透视 projections: all projectors投影线 meet at the center of projection投影中心
- Parallel平行 projection: projectors投影线 are parallel, center of projection is replaced by a direction of projection投影方向
- Clipping and Primitive Assembly 裁减 与 图元组装
- Clipping must be done on a primitive-by-primitive basis. Thus, within the stage of the pipline, we must assemble sets of vertices into primitives, such as line segments and polygons, before clipping can take place. The output of this stage is a set of primitives whose projections can appear in the iamge.
- 透视投影和平行投影都有一个对应的裁剪体,Objects that are not within this volume are said to be clipped out of the scene
- Rasterization光栅化
The output of the rasterizer is a set of fragments for each object. A fragment can be thought as a pixel the carryies with its information, including
- Have a location in frame buffer位置信息
- Color attributes颜色属性
- Depth information深度信息
- Fragment Processing 片元处理
包括光照和明暗绘制(lighting and shading),纹理映射(texture mapping),凹凸映射(bump mapping),消隐(Hidden-surface removal)等。
chapter2
OpenGL 与 WebGL简介
- OpenGL(英语:Open Graphics Library,译名:开放图形库或者“开放式图形库”)是用于渲染2D、3D矢量图形的跨语言、跨平台的应用程序编程接口(API)。这个接口由近350个不同的函数调用组成,用来从简单的图形比特绘制复杂的三维景象
- WebGL(全写Web Graphics Library)是一种3D绘图协议,这种绘图技术标准允许把JavaScript和OpenGL ES 2.0结合在一起,通过增加OpenGL ES 2.0的一个JavaScript绑定,WebGL可以为HTML5 Canvas提供硬件3D加速渲染,这样Web开发人员就可以借助系统显卡来在浏览器里更流畅地展示3D场景和模型了,还能创建复杂的导航和数据视觉化。显然,WebGL技术标准免去了开发网页专用渲染插件的麻烦,可被用于创建具有复杂3D结构的网站页面,甚至可以用来设计3D网页游戏等等。
OpenGL 与WebGL函数的使用
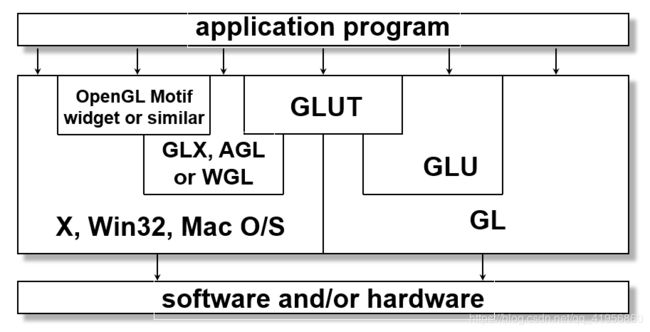
- OpenGL Libraries
- OpenGL core Library
- OpenGL utility Library(GLU) :Provides functionality in OpenGL core but avoids having to rewrite code
- Links with window system
- GLX for X window systems (X window窗口扩展库)
- WGL for Windows (PC window窗口扩展库)
- AGL for Macintosh (苹果window窗口扩展库)
- OpenGL Utility Toolkit (GLUT) 实用程序工具包: Provides functionality common to all window systems,Code is portable移植 but GLUT lacks the functionality of a good toolkit for a specific platform
- glew : OpenGL扩展库
- features(function format, etc.)
opengl基本函数分类
| 函数 | 说明 | 例 |
|---|---|---|
| 图元函数 | 控制绘制图元 | glPolygonMode(),glDrawArray()1 |
| 属性函数 | 颜色属性、填充模式 | glClearColor()2, glEnable()13 |
| 观察函数 | ||
| 变换函数 | 生成变换矩阵 | |
| 输入函数 | 接收输入设备的输入,回调函数 | |
| 控制函数 | 初始化程序、与窗口通信 | glutInit()3,glutCreateWindow()4, glViewPort()5,…6 |
| 查询函数 | 查询设备参数等 | |
| 帧缓存 | - | glGenBuffers()7, glBbindBuffer()8,glBufferData()9 |
| 着色器输入 | - | glGetAtrribLocation()10, glEnableVertexArray(), glVertexAttrib()11, glVertexAttribPointer()12 |
- glDrawArray
void glDrawArrays( GLenum mode,
GLint first,
GLsizei count);
- mode: Symbolic constants GL_POINTS, GL_LINE_STRIP, GL_LINE_LOOP, GL_LINES, GL_LINE_STRIP_ADJACENCY, GL_LINES_ADJACENCY, GL_TRIANGLE_STRIP, GL_TRIANGLE_FAN, GL_TRIANGLES, GL_TRIANGLE_STRIP_ADJACENCY, GL_TRIANGLES_ADJACENCY and GL_PATCHES are accepted.
- first
Specifies the starting index in the enabled arrays. - count
Specifies the number of indices to be rendered.
- glClearColor(): specify clear values for the color buffers
void glClearColor( GLfloat red, GLfloat green, GLfloat blue, GLfloat alpha);
- glutInit(int *agrc, char**argv);
- glutCreateWindow(char *title);
- void glViewport( GLint x, GLint y, GLsizei width, GLsizei height);
左下角为原点 - glutMainLoop()
void glutDisplayFunc(void (*func)(void)) 显示回调函数 - void glGenBuffers( GLsizei n, GLuint * buffers);
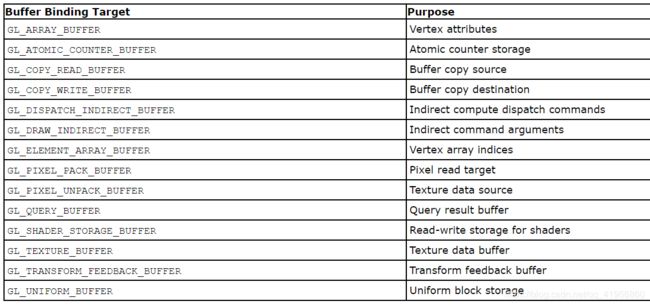
- void glBindBuffer( GLenum target, GLuint buffer);
- target: Specifies the target to which the buffer object is bound, which must be one of the buffer binding targets in the following table:
- void glBufferData(GLenum target, GLsizeiptr size, const void * data, GLenum usage);
- example: flBufferData(GL_ARRAY_BUFFER, sizeof(points), points, GL_STATIC_DRAW);
- usage: Specifies the expected usage pattern of the data store. The symbolic constant must be GL_STREAM_DRAW, GL_STREAM_READ, GL_STREAM_COPY, GL_STATIC_DRAW, GL_STATIC_READ, GL_STATIC_COPY, GL_DYNAMIC_DRAW, GL_DYNAMIC_READ, or GL_DYNAMIC_COPY.
- GLint glGetAttribLocation( GLuint program, const GLchar *name);
Returns the location of an attribute variable - glVertexAttrib — Specifies the value of a generic vertex attribute. including a group of functions. e.g
void glVertexAttrib1f( GLuint index, GLfloat v0); void glVertexAttribPointer( GLuint index, GLint size, GLenum type, GLboolean normalized, GLsizei stride, const void * pointer);
define an array of generic vertex attribute data- void glEnable( GLenum cap);
- cap: Specifies a symbolic constant indicating a GL capability.
| value | explanlation |
|---|---|
| GL_BLEND | If enabled, blend the computed fragment color values with the values in the color buffers. See glBlendFunc. |
| GL_CULL_FACE | If enabled, cull polygons based on their winding in window coordinates. See glCullFace. |
| GL_DEBUG_OUTPUT | If enabled, debug messages are produced by a debug context. When disabled, the debug message log is silenced. Note that in a non-debug context, very few, if any messages might be produced, even when GL_DEBUG_OUTPUT is enabled. |
| GL_DEPTH_TEST | If enabled, do depth comparisons and update the depth buffer. Note that even if the depth buffer exists and the depth mask is non-zero, the depth buffer is not updated if the depth test is disabled. See glDepthFunc and glDepthRange. |
| GL_DITHER | If enabled, dither color components or indices before they are written to the color buffer |
| GL_LINE_SMOOTH | If enabled, draw lines with correct filtering. Otherwise, draw aliased lines. See glLineWidth |
| GL_POLYGON_SMOOTH | If enabled, draw polygons with proper filtering. Otherwise, draw aliased polygons. For correct antialiased polygons, an alpha buffer is needed and the polygons must be sorted front to back. |
| GL_SAMPLE_ALPHA_TO_ONE | If enabled, each sample alpha value is replaced by the maximum representable alpha value. |
| GL_STENCIL_TEST | If enabled, do stencil testing and update the stencil buffer. See glStencilFunc and glStencilOp. |
| … | https://www.khronos.org/registry/OpenGL-Refpages/gl4// |
指定OpenGL窗口的显示模式的函数是什么?并给出互斥参数的比较分析。
- glutInitDisplayMode()
参数:
- 颜色模式:GLUT_RGBA,GLUT_RGB 和 GLUT_INDEX(颜色索引)
- 缓冲区类:GLUT_DOUBLE,GLUT_SINGLE
- 深度缓存:GLUT_DEPTH
- 模板缓存:GLUT_STENCIL
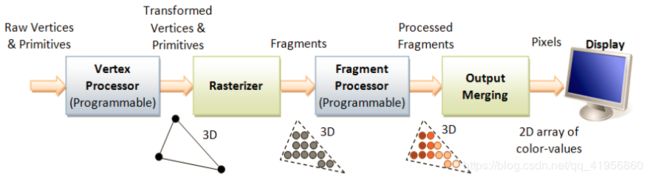
WebGL的绘制流水线
- 如上图所示,主要分为4个步骤,第1步是顶点着色器的处理,主要是一组矩阵变换操作,用来把3D模型(顶点和原型)投影到Viewport上,输出是一个个多边形(比如三角形),第2步是光栅化,也就是把三角形连接区域按一定的粒度逐行转化成片段(fragement),我们可以把这些片段看做是3D空间的像素点,第3步是片段着色器的处理,为每个像素添加颜色,第4步把3D空间的片段合并输出为2D像素数组输出到帧缓存然后显示在屏幕上。
颜色索引(C51)
chapter3
双缓存 C75
物理设备(C7)(多种类型)与逻辑设备(C9)(6种基本类型)
-
物理设备:
定位设备,键盘设备,鼠标,操纵杆,空间球等eg. mouse, trackball, light pen, data tablet, joy stick, space ball -
逻辑输入设备:
Locator(定位设备): 返回一个位置(鼠标)
Pick(逻辑拾取设备): 返回对象的标识ID(鼠标)
Keyboard: 返回字符串(键盘)
Stroke:返回一系列位置
Valuator(定值设备): 返回浮点数(滑杆)
Choice(选择设备): 返回n项中的一项(菜单) -
物理设备与逻辑设备区别?
为使应用程序独立于具体使用的物理设备,引入逻辑设备和物理设备两个概念,在应用程序中,用来请求I/O服务而使用的是逻辑设备,系统在实际执行时使用的是物理设备,系统为了实现从逻辑设备到物理设备的映射,设置了一张逻辑设备表。每个表目包括逻辑设备名、物理设备名、设备驱动程序入口。这样做实现了设备独立性,带来两个好处:使设备分配时具有灵活性和易于实现I/O重定向。
三种基本的输入模式(请求、采样、事件)C10
- 请求模式(request mode):除非设备被触发,否则设备的测量数据不会返回给程序
- 采样模式(sample mode):输入时即时的,只要在用户程序中遇到了函数调用,就把测量数据返回给程序,因此不需要触发器
- 事件模式(event mode):有多个设备的输入时,每个输入设备都有它自己的触发器并运行一个测量过程。每当一个设备被触发,就产生了一个事件。设备的测量数据(包括该设备的标志符)被放入一个事件队列中。
之后应用程序处理事件的方式:1、用户程序检查事件队列中排在前面的事件,或如果队列为空则等待,直到有事件发生检查事件的类型然后决定做什么。2、对每一种特定类型的事件关联一个叫做回调的函数,操作系统定期检查事件队列中的事件,并且针对事件的类型执行相应的回调函数。
GLUT的基本回调函数(显示、鼠标、形变、键盘、空闲等)C57,72
- GlutDisplayFunc(mydisplay) //显示回调
glutMouseFunc(mymouse) //鼠标左右键和中键摁下的事件
glutReshapeFunc //形状改变~
glutKeyboardFunc //键盘~
glutIdleFunc //空闲~
glutMotionFunc //当鼠标键摁下时,鼠标拖动的事件。当鼠标拖动时,将每一帧都调用一次这个函数。
glutPassiveMotionFunc //当没有鼠标键摁下时,鼠标拖动的事件。当鼠标拖动时,…(同上) - 调用过程:事件循环语句glutMainLoop();使程序进入一个无穷的事件循环,每经过事件循环一次,GLUT即查看事件队列中的事件,如果定义了相应的回调函数即执行,否则忽略该事件。
- 显示回调函数:只要GLUT确定需要刷新窗口(当第一次打开窗口,改变了窗口形状,重新露出窗口,当用户程序决定需要改变显示内容的时候),那么就会执行显示回调函数。(每个GLUT程序都必须有一个显示回调函数,必要时可以设置为空函数)。许多事件都会导致调用显示回调函数,避免一次事件循环过程中多次执行:glutPostRedisplay();(通过设置标志—检查是否设置标志决定是否执行显示回调函数)。
chapter4
标量、向量、点的概念 C82
- point:三维空间中,点是空间中一个位置
- Scalar:服从一组规则的对象,这些规则是从普通的算数运算中抽象出来的。
- Vectors
• Physical definition: a vector is a quantity with two attributes
Direction方向
Magnitude长度
仿射空间
- 定义:仿射空间是点和向量的集合 [1] ,它的定义是:
- (1)设A为一个点集,A中任意两个有序点P、Q对应于n维矢量空间中的一个矢量a;
- (2)设P、Q、R为A中任意三点,P、Q对应于矢量a,Q、R对应于矢量b,则P、R对应于矢量a+b。
具有上面两个性质的点集A就叫做一个仿射空间。
- 运算:定义了两种运算
- 点加上向量得到点
- 点点做差得到向量(点与点之间没有加法运算)
- 仿射空间是没有起点只有方向与大小的向量所构成的向量空间。
- 线性变换的几何意义是图像的旋转和变形,而仿射变换的几何意义是旋转和变性再加上位移,所以仿射变换也可以表示为线性变换再加上位移。用矩阵表示的话,线性变换是 y = Ax,而仿射变换是 y = Ax + b。
点积和叉积(图形学意义)C88
维数、基、坐标系与标架 C91
- 维数:In a vector space, the maximum number of linearly independent vectors is fixed and is called the dimension of the space
- 基:In an n-dimensional space, any set of n linearly independent vectors form a basis for the space
- 坐标系:在n维坐标系中,任意n个线性无关的向量v1、v2…vn可定义一个坐标系。
- 标架:原点和基向量决定了一个标架
Within this frame, every vector can be written as
v = a 1 v 1 + a 2 v 2 + … . + a n v n v=a1v1+ a2v2 +….+anvn v=a1v1+a2v2+….+anvnand every point can be written as
P = P 0 + b 1 v 1 + b 2 v 2 + … . + b n v n P = P0 + b1v1+ b2v2 +….+bnvn P=P0+b1v1+b2v2+….+bnvn
Consider the point and the vector.They appear to have the similar representations
p = [ b 1 b 2 b 3 ] v = [ a 1 a 2 a 3 ] p=[b1\ b2\ b3] \ \ \ \ \ \ \ \ v=[a1\ a2\ a3] p=[b1 b2 b3] v=[a1 a2 a3]
which confuses the point with the vector
Homogeneous Coordinates C95
齐次坐标定义:将一个原本是n维的向量用一个n+1维向量来表示,是指一个用于投影几何里的坐标系统。
-
definition of Homogeneous Coordinates
- A Single Representation
We can write a vector v and a point P as( where P0 is the origin)
v = a 1 v 1 + a 2 v 2 + a 3 v 3 = [ a 1 a 2 a 3 0 ] [ v 1 v 2 v 3 P 0 ] T \ v=a1v1+ a2v2 +a3v3 = [a1\ a2\ a3\ 0 ] [v1\ v2\ v3\ P0]^T v=a1v1+a2v2+a3v3=[a1 a2 a3 0][v1 v2 v3 P0]T P = P 0 + b 1 v 1 + b 2 v 2 + b 3 v 3 = [ b 1 b 2 b 3 1 ] [ v 1 v 2 v 3 P 0 ] T P = P0 + b1v1+ b2v2 +b3v3= [b1\ b2\ b3\ 1 ] [v1\ v2\ v3\ P0]^T P=P0+b1v1+b2v2+b3v3=[b1 b2 b3 1][v1 v2 v3 P0]T
Thus we obtain the four-dimensional homogeneous coordinate representation
v = [ a 1 a 2 a 3 0 ] T v = [a1\ a2\ a3\ 0 ] T v=[a1 a2 a3 0]T p = [ b 1 b 2 b 3 1 ] T p = [b1\ b2\ b3\ 1 ] T p=[b1 b2 b3 1]T - If w=0, the representation is that of a vector
p =[x’ y’ z’ w] T =[wx wy wz w] T - For w=1, the representation of a point is [x y z 1]
- The homogeneous coordinates form for a three dimensional point [x y z] is given as
p = [ x ’ y ’ z ’ w ] T = [ w x w y w z w ] T p =[x’\ y’\ z’\ w] T =[wx\ wy\ wz\ w] T p=[x’ y’ z’ w]T=[wx wy wz w]TWe return to a three dimensional point (for w¹0) by
x = x ’ / w x=x’/w x=x’/w y = y ’ / w y=y’/w y=y’/w z = z ’ / w z=z’/w z=z’/w
- A Single Representation
-
use of Homogeneous Coordinates
- All standard transformations (rotation, translation, scaling) can be implemented with matrix multiplications using 4 x 4 matrices
- Hardware pipeline works with 4 dimensional representations
三种基本变换:平移、旋转、缩放(2D与3D)C111
- translation平移: T − 1 ( d x , d y , d z ) = T ( − d x , − d y , − d z ) T^{-1}(dx, dy, dz) = T(-dx, -dy, -dz) T−1(dx,dy,dz)=T(−dx,−dy,−dz)
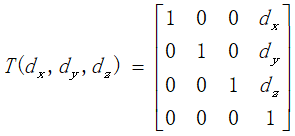
- rotation: R − 1 ( q ) = R ( − q ) R^{-1}(q) = R(-q) R−1(q)=R(−q)
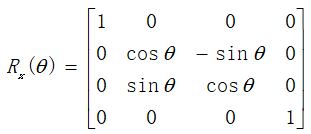
- Scaling
S − 1 ( s x , s y , s z ) = S ( 1 / s x , 1 / s y , 1 / s z ) S^{-1}(sx, sy, sz) = S(1/sx, 1/sy, 1/sz) S−1(sx,sy,sz)=S(1/sx,1/sy,1/sz)
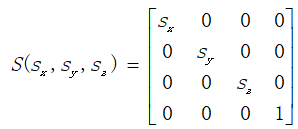
组合变换(顺序问题)C117
坐标系的变换是几何变换的一个工具。
通常我们要在原坐标系 C0 执行一种变换 M0,但在原坐标系中难以通过基本的旋转平移来计算。所以我们使用一个辅助坐标系 C1,先将C0中的坐标变换到C1中,变换矩阵为Ma。然后把C0中的变换M0等价为C1中的变换M1,最后C1中的坐标还原回C0。得到组合变换矩阵 M α − 1 M 1 M α M_\alpha^{-1}M_1M_\alpha Mα−1M1Mα
以下面的例子为例,在原坐标系中有两次变换。第一次相对y=x做变换,可以构造一个以y=x为轴的坐标系。第二次相对x=1变换,可以构造一个以 x=1为轴的坐标系。
- 已知三角形ABC各顶点的坐标A(1,2)、B(5,2)、C(3,5),相对先直线y=x做对称变换再相对于直线x=1做对称变换,最终得到三角形A’B’C’,请给出变换方法,写出相应的组合变换矩阵,并计算三角形A’B’C’的坐标
- 注意,若向量用列向量表示,级联的顺序是从右到左
- 坐标变换原理
设 { v 1 , v 2 , v 3 } \{\textbf{v}_1, \textbf{v}_2, \textbf{v}_3\} {v1,v2,v3} 和 { u 1 , u 2 , u 3 } \{\textbf{u}_1, \textbf{u}_2, \textbf{u}_3\} {u1,u2,u3} 是两组基。
定义一个矩阵
M = [ γ 11 γ 12 γ 13 γ 21 γ 22 γ 23 γ 31 γ 32 γ 33 ] \textbf{M}=\begin{bmatrix}\gamma_{11} &\gamma_{12} & \gamma_{13} \\ \gamma_{21} &\gamma_{22} & \gamma_{23} \\ \gamma_{31} &\gamma_{32} & \gamma_{33} \\ \end{bmatrix} M=⎣⎡γ11γ21γ31γ12γ22γ32γ13γ23γ33⎦⎤
有, [ u 1 u 2 u 3 ] = M [ v 1 v 2 v 3 ] \begin{bmatrix} \textbf{u}_1 \\ \textbf{u}_2 \\ \textbf{ u}_3 \end{bmatrix} = \textbf{M} \begin{bmatrix} \textbf{v}_1 \\ \textbf{v}_2 \\ \textbf{v}_3 \end{bmatrix} ⎣⎡u1u2 u3⎦⎤=M⎣⎡v1v2v3⎦⎤
令 T = M − 1 \textbf{T} = \textbf{M}^{-1} T=M−1
则对于一个坐标(或者向量) w = β 1 v 1 + β 2 v 2 + β 3 v 3 \textbf{w}=\beta_1\textbf{v}_1+\beta_2\textbf{v}_2+\beta_3\textbf{v}_3 w=β1v1+β2v2+β3v3,
用第二组基表示 w ‘ = α 1 u 1 + α 2 u 2 + α 3 u 3 \textbf{w}`=\alpha_1\textbf{u}_1+\alpha_2\textbf{u}_2+\alpha_3\textbf{u}_3 w‘=α1u1+α2u2+α3u3,
则 [ α 1 α 2 α 3 ] = T [ β 1 β 2 β 3 ] \begin{bmatrix}\alpha_1 \\ \alpha_2 \\ \alpha_3 \end{bmatrix} = \textbf{T} \begin{bmatrix} \beta_1 \\ \beta_2 \\ \beta_3 \end{bmatrix} ⎣⎡α1α2α3⎦⎤=T⎣⎡β1β2β3⎦⎤
多边形网格、多面体、欧拉公式(CG14) 、四元数(C132,CG13)
-
多边形网格
由多边形彼此相接构成的网格,多边形称为网格的面,多边形的顶点也称为网格的顶点。一般要求两张相邻面的公共边完全相同,即不能出现某一面的一个顶点在另一面的边中间 -
多边形网格的类型
- 实体,多边形网格形成一个 封闭的空间区域
- 表面,不形成空间封闭区域,表示一个 无限薄的曲面
两者都称为多边形网格(polygonal mesh),有时简称为网格
-
网格组成的对象的可能的性质
- 实体:如果网格形成一个封闭的有界区域
- 连通性:如果任两个顶点间存在着由边构造的连续路径
- 简单性:表示一个实体,而且没有洞,即可以(没有粘贴)变形到球面
- 平面性: 如果所有面都是平面多边形
-
多面体是由简单表面(平面)构造的连通网格,其形成一个有限体积的封闭实体
- 多面体的每边都有两个面共享
- 每个顶点至少有三条边
- 两个面之间要么无交,要么只在公共边或顶点处相交
- 四面体为多面体,环面为多面体当且仅当各面为平面
-
欧拉公式
在任何一个规则球面地图上(简单多面体),用 F记区域个 数 ,V记顶点个数 ,E记边界个数 ,则
F + V − E = 2 F + V- E= 2 F+V−E=2 -
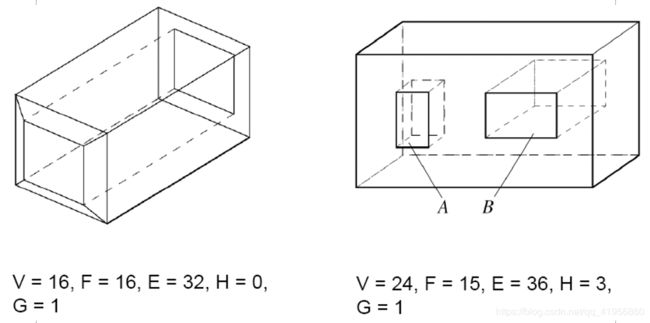
扩展的Euler公式
如果多面体不是简单的,在面上有H个洞,通过多面体的洞有G个,那么
V + F – E = 2 + H – 2 G V + F – E = 2 + H – 2G V+F–E=2+H–2G
-
四元数
Quaternions can express rotations on sphere smoothly and efficiently.
Process:- Model-view matrix -> quaternion
- Carry out operations with quaternions
- Quaternion -> Model-view matrix
-
旋转
- 点:p = (0, Q)
- 定义四元数:r = (cosθ/2, sin θ/2 v), 其中v为一个单位向量
- rpr−1得到点Q绕方向v旋转θ角后的位置
chapter5
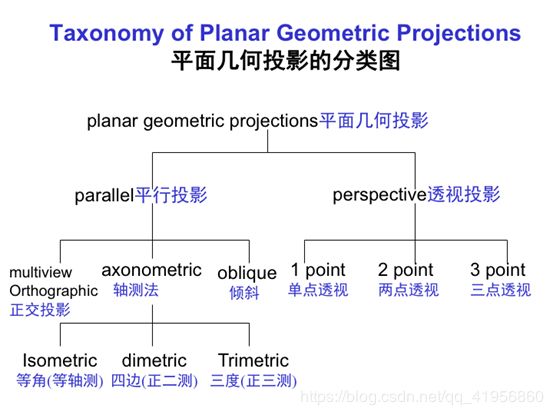
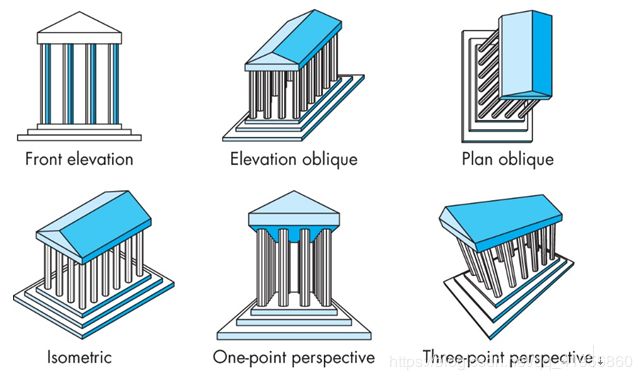
平面几何投影的分类(平行与透视)C139
-
平面几何投影:投影到平面上的标准投影。投影线为直线,这些直线汇聚于投影中心,或者彼 此平行。这种投影保持共线性,但不一定保角。
-
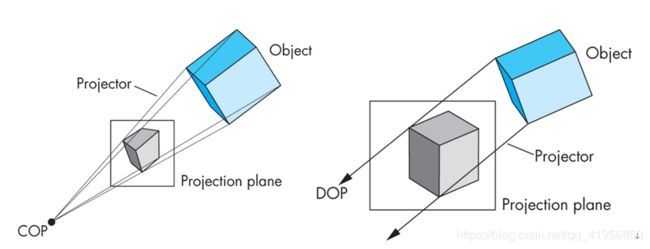
平行投影:投影中心与投影面之间的距离为无限,因此,只需给出投影方向即可。平行投 影是透视投影的极限状态。
优势与不足:1)保持了距离与角度 2)不能看到对象真正的全局形状,因为许多面在视点中不可见。 -
透视投影:投影线回聚于投影中心(COP)
优势与不足:1)同样大小的对象,离视点越远,投影结果就越小,但是看起来 更真实。 2)在一条直线等距离的几点投影后不一定等距(非均匀收缩)。 3)只有在平行于投影面的平面上角度被保持。 4)相对于平行投影而言,更难用手工进行绘制(但对计算机而言, 没有增加更多的困难。) -
平行投影和透视投影相似点:
- 观察的基本元素相同,包括对象、观察者、投影线、投影平面
不同领域的经典视图 C139
灭点的概念 C142
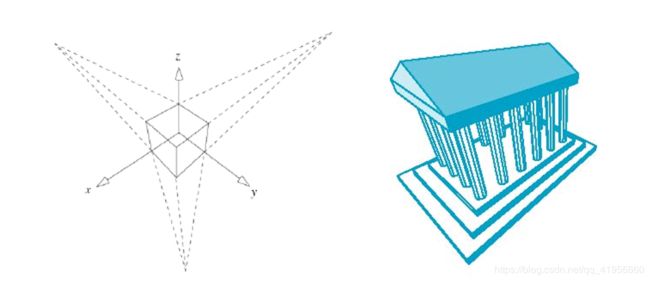
Parallel lines (not parallel to the projection plan) on the object converge at a single point in the projection (the vanishing point) 
- 主灭点:平行于坐标轴的平行线的灭点。
主灭点的个数决定- 一点透视
- 两点透视
- 三点透视
建立观察标架 C143、CG16
There are three aspects of the viewing process, all of which are implemented in the pipeline
- Positioning the camera定位照相机
- Setting the model-view matrix设置模型-视图矩阵
- Selecting a lens设置镜头
- Setting the projection matrix设置投影矩阵
- Clipping裁剪
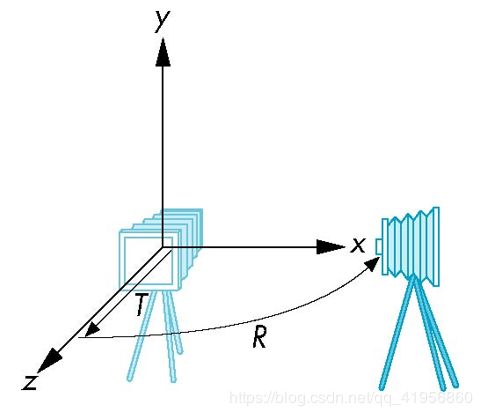
照相机标架的定位 C144
本质上是把照相机放在原点上考虑如何移动物体。只不过我们先考虑怎么移动相机,再把相机移动等效成物体移动。
如下面这个图是为了得到物体的侧视图。
- 首先需要照相机绕y轴旋转90°,相应的物体旋转-90°。对应的变换矩阵R=Ry(-90)
- 然后然后将相机移动,注意这个时候在对象标架中相机是向x方向移动,但实际考虑的是如何在照相机标架中移动物品,所以要沿z轴负方向移动。对应的变换矩阵 T=Tz(-d)
- 最后得到组合变换 model_view=TR
(1)通过一系列旋转平移来改变模-视变换矩阵,从而间接的指定照相机方位。(如上面的举例)
(2)通过API来指定照相机的方位,首先在对象标架下面描述照相机的方位,第二步骤指定想要获得的投影的类型(规范化变换),接下来指定照相机的方向,指定观察平面的法向量(VPN),指定观察的正向向量(VUP),VUP向量投影到观察平面上面得到方向向上的向量v,向量v和向量n()正交得到第三个向量u,这个坐标系就被成为观察坐标系,加上VRP(观察参考点 第五版p186)就是观察标架
其它视图API(如Yaw、Pitch、Roll,方位角、仰角)C150
投影规范化 C153 C162 CG17
- All other views are converted to the default view by transformations that determine the projection matrix 由投影矩阵确定的变换把所有其它的视图转化为默认视图
- Allows use of the same pipeline for all views 从而可以对所有的视图采用同样的流水线体系
- Normalization allows for a single pipeline for both perspective and orthogonal viewing规范化使得只需要一个流水线体系就可以进行透视投影和正交投影
- We stay in four dimensional homogeneous coordinates as long as possible to retain three-dimensional information needed for hidden-surface removal and shading尽可能位于四维齐次空间中,以便保持隐藏面消除和明暗处理所需要的三维信息
- We simplify clipping简化了裁剪的操作
无论是平行投影还是透视投影,先进行投影规范化,将视见体转化为标准视见体,然后执行透视除法,便可以统一使用正交投影得到最终结果。
chapter 6
Phong光照模型三个分量:环境光、漫反射光、镜面反射光 C186、 CG18
-
Uses four vectors四个向量
• To source光源方向 I
• To viewer视点方向 v
• Normal法向n
• Perfect reflector理想反射方向r -
Ambient环境光:环境内均匀的照明,环境光强度在物体表面所有点都是相同的,但由于材质的差异,反射系数不同。
I a = k a L a I_a = k_aL_a Ia=kaLa -
Diffuse漫反射光:入射光线向各个方向散射,理想漫反射表面向各个方向散射的光线强度相同,因此不同位置的观察者看到的反射光线一样,被称之为Lambert 表面。同时,更加Lambert定律,只有入射光线的垂直分量才对照明起作用(中午地面反射的光比下午强)。
I d = k d a + b d + c d 2 m a x ( ( l ⋅ n ) L d , 0 ) I_d=\frac{k_d}{a+bd+cd^2}max((\textbf{l}\cdot\textbf{n})L_d,0) Id=a+bd+cd2kdmax((l⋅n)Ld,0) l \textbf{l} l是光源方向, n \textbf{n} n是法向量,d是距离,a、b、c是衰减系数,k是反射系数,Ld是漫反射光强度 -
Specular镜面反射光:反射的光线集中在反射角附近,因此看起来有光泽。理想的镜面反射所有光都沿反射角反向。
I s = k s a + b d + c d 2 m a x ( ( r ⋅ v ) α L d , 0 ) I_s=\frac{k_s}{a+bd+cd^2}max((\textbf{r}\cdot\textbf{v})^\alpha L_d,0) Is=a+bd+cd2ksmax((r⋅v)αLd,0) r \textbf{r} r是反射角方向, v \textbf{v} v是观察者, α \alpha α是高光系数(shininess)。
反射系数与高光系数 C188
中值向量与改进Phong光照模型 C189、CG19
Gouraud模型与Phong模型的明暗处理对比 C193、CG19
-
相同点:
-
不同点:
-
Gouraud明暗处理只在多边形顶点处采用Phong局部反射模型计算光强,而在多边形内的其他点采用双向线性插值,这样做的优点是高效,但是无法很好的处理镜面高光问题,依赖于其所在多面形的相对位置;
而Phong明暗处理,通过差值计算每个顶点的法向量3次差值(在x,y,z三个方向分别进行差值计算),然后计算每个点上的光强值,这样效果好,但计算复杂,需要付出比Gouraud 4-5 倍的时间。 -
绘制方法
Gouraud Shading:
1. Find average normal at each vertex (vertex normals)
2. Apply modified Phong model at each vertex
3. Interpolate vertex shades across each polygon
Phong Shading
5. Find vertex normals
6. Interpolate vertex normals across edges
7. Interpolate edge normals across polygon
8. Apply modified Phong model at each fragment片元 -
通常,在一个比较复杂的场景中,当物体镜面发射很微弱时,我们对其采用Gouraud明暗处理,而对于一些镜面高光的物体,采用Phong明暗处理,这样既保证质量,又保证速度。
-
If the polygon mesh approximates surfaces with a high curvatures, Phong shading may look smooth while Gouraud shading may show edges. 如果用多边形网格逼近大曲率曲面,Phong方法的结果可能看起来光滑一些,而Gouraud方法就会使边有些明显
-
Phong shading requires much more work than Gouraud shading Phong.Until recently not available in real time systems。Phong方法比Gouraud方法的复杂度高,直到现在,在实时系统中还不可用
可以用片段处理器实现 -
Now can be done using fragment shaders (see Chapter 9)可以用片元处理器实现
-
Both need data structures to represent meshes so we can obtain vertex normals 两种方法都需要特定数据结构表示网格,从而可以获取顶点法向量
均匀着色
在同一多边形上法向n为常向量
视点在无穷远,视点方向v是常向量
光源在无穷远,入射方向l也是常向量
从而对于每个多边形,只需要计算其上一点的颜色,其它点的颜色与它相同
OpenGL里,下面函数定义平面明暗处理效果 glShadeModel(GL_FLAT);
平滑着色
- 在网格中每个顶点处有几个多边形交于该点,每个多边形有一个法向,取这几个法向的平均化得到该点的法向
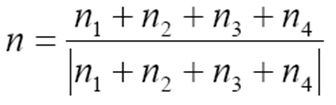
- 然后利用简单光照模型计算出顶点的颜色
- 对于多边形内的点,采用线性插值确定颜色
- OpenGL中设置光滑明暗处理
glShadeModel(GL_SMOOTH);
Phong着色
- 与Gouraud方法不同,Phong方法是根据每个顶点的法向,插值出多边形内部各点的法向,然后基于光照模型计算出各点的颜色
Chapter 8
面向图像与面向对象的方法C214、CG21
-
面向图像(image-oriented)的方法,面向对象(object-oriented)的方法也分别称为, 先排序(sort-first),后排序(sort-last)方法,基于隐藏面消除发生的地方进行命名的
-
面向对象方法优缺点:
• 优点:处理速度快,运行成本低
• 缺点:- 过去需要占用大量内存,每个对象单独处理的代价较大。由于低价大容量内存,以及专用硬件芯片的出现,已不再是问题
- 不能得到大多数全局效果,例如涉及多个对象的复杂光照
• 隐藏面消除例外,Z buffer全局深度信息
-
面向图像方法优缺点:
• 优点:- 任何时刻只需有限的显示内存,且可以按显示器的刷新速度和次序生成像素
- 利用相邻像素间的连贯性可设计增量式算法
- 适合处理全局效果
• 缺点:
- 需要复杂的几何对象的数据结构
- 必须确定哪些图元影响哪些像素
- 绘制过程中需要随时访问所有的几何数据
隐藏面消除 的对象空间和图像空间消隐算法 C235
线段的裁剪:Cohen-Sutherland法(区域编码)、Liang-Barsky法(参数顺序) C218、CG21
- Cohen-Sutherland Algorithm
• Idea: eliminate as many cases as possible without computing intersections
• Start with four lines that determine the sides of the clipping window从
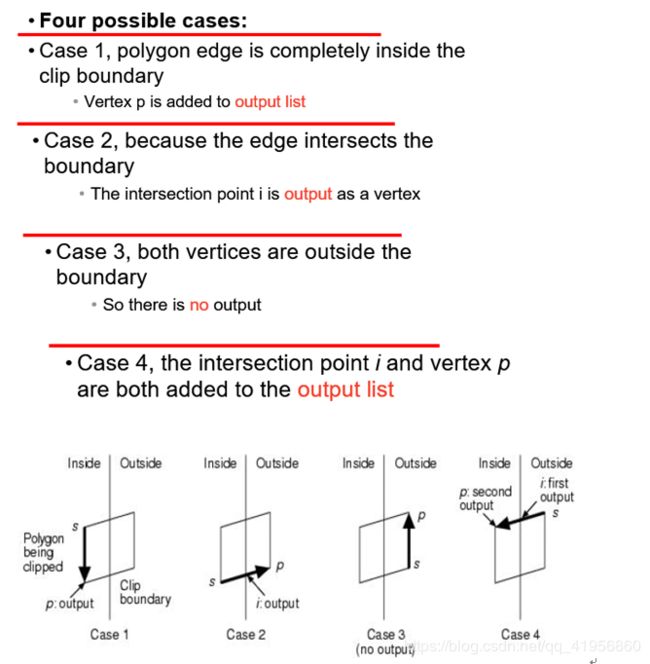
多边形的裁剪:Sutherland-Hodgeman算法(裁剪与重构的4种情况)C222、CG22
文本裁剪的方法(字符串、字符、矢量)C225、CG22
画家算法(C241)与深度缓存算法(C238)(Z-Buffer)CG22
画家算法就是一种对象空间消隐算法,需要对对象进行深度排序,有个缺点——难以直接处理嵌套重叠等复杂情况。
Z-buffer算法是一种图像空间消隐算法
线段的扫描转换:DDA、Bresenham(中点画线算法)C229、CG23
多边形的扫描转换:ET、AET、奇偶规则(C232)、特殊情况处理(C234) CG23
走样(若干现象)与反走样(两种方法)C243、CG23
chapter11
曲线曲面的表达方式:显示、隐式、参数 C355
- 显示:z=f(x, y)
- 隐式:f(x, y, z)=0
- 参数
p ( u ) = [ p x ( u ) p y ( u ) p z ( u ) ] = c 0 + c 1 u + c 2 u 2 + c 3 u 3 = ∑ k = 0 3 c k u k = u T c \textbf{p}(u)=\begin{bmatrix}p_x(u)&p_y(u)&p_z(u)\end{bmatrix}=\textbf{c}_0+\textbf{c}_1u+\textbf{c}_2u^2+\textbf{c}_3u^3=\sum^3_{k=0}{\textbf{c}_ku^k}=\textbf{u}^T\textbf{c} p(u)=[px(u)py(u)pz(u)]=c0+c1u+c2u2+c3u3=k=0∑3ckuk=uTc其中
c = [ c 0 c 1 c 2 c 3 ] u = [ 1 u u 2 u 3 ] c k = [ c k x c k y c k z ] \textbf{c}=\begin{bmatrix}\textbf{c}_0\\\textbf{c}_1\\ \textbf{c}_2 \\\textbf{c}_3\end{bmatrix}\ \ \ \textbf{u}=\begin{bmatrix}1 \\u \\u^2\\u^3\end{bmatrix}\ \ \ \ \textbf{c}_k=\begin{bmatrix}c_{kx}\\ c_{ky}\\ c_{kz}\end{bmatrix} c=⎣⎢⎢⎡c0c1c2c3⎦⎥⎥⎤ u=⎣⎢⎢⎡1uu2u3⎦⎥⎥⎤ ck=⎣⎡ckxckyckz⎦⎤
写成分量形式等价为:
p x ( u ) = c 0 x + c 1 x u + c 2 x u 2 + c 3 x u 3 p y ( u ) = c 0 y + c 1 y u + c 2 y u 2 + c 3 y u 3 p z ( u ) = c 0 z + c 1 z u + c 2 z u 2 + c 3 z u 3 p_x(u)=c_{0x}+c_{1x}u+c_{2x}u^2+c_{3x}u^3\\p_y(u)=c_{0y}+c_{1y}u+c_{2y}u^2+c_{3y}u^3\\p_z(u)=c_{0z}+c_{1z}u+c_{2z}u^2+c_{3z}u^3 px(u)=c0x+c1xu+c2xu2+c3xu3py(u)=c0y+c1yu+c2yu2+c3yu3pz(u)=c0z+c1zu+c2zu2+c3zu3
三次曲线: Hermite(C363)、Bezier(C366)、B-spline (C368)
- 参数连续性
- C 0 \textbf{C}^0 C0参数连续性:连接处值相等
- C 1 \textbf{C}^1 C1参数连续性:连接处值相等且导数相等,可推广得到 C n \textbf{C}^n Cn参数连续性
- G 1 \textbf{G}^1 G1几何连续性:连接处值相等且切向向量成比例,可推广得到 G n \textbf{G}^n Gn几何连续性
- Hermite
通过两个断点(u=0,u=1)及端点处的导数来计算曲线的参数方程。Bezier相当于是Hermite的一种具体的实现算法。 - Bezier
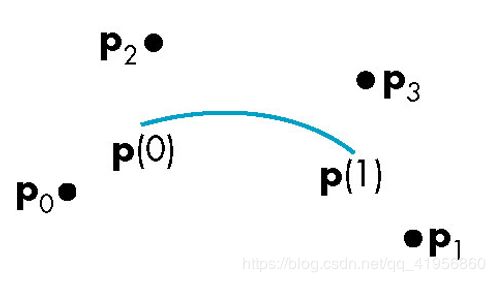
有4个控制点 p 0 , p 1 , p 2 , p 3 \textbf{p}_0,\textbf{p}_1,\textbf{p}_2,\textbf{p}_3 p0,p1,p2,p3。使用 p 0 , p 3 \textbf{p}_0,\textbf{p}_3 p0,p3作为u=0,1时曲线上的点,即 p ( 0 ) , p ( 1 ) \textbf{p}(0),\textbf{p}(1) p(0),p(1)。使用如下近似公式拟合曲线在u=0,1的切线。
p ′ ( 0 ) ≈ p 1 − p 0 1 / 3 p ′ ( 1 ) ≈ p 3 − p 2 1 / 3 \textbf{p}'(0) \approx \frac{\textbf{p}_1-\textbf{p}_0}{1/3}\\\textbf{p}'(1) \approx \frac{\textbf{p}_3-\textbf{p}_2}{1/3} p′(0)≈1/3p1−p0p′(1)≈1/3p3−p2
通过这4个点求得参数 c \textbf{c} c。
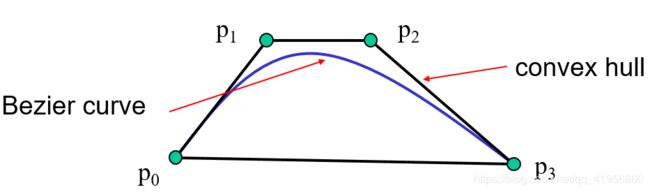
局限在于只有C0连续性
chapter12
光线跟踪(Ray tracing)概念 C391 CG40
- 光线跟踪是一种渲染算法,该算法模拟灯光穿过场景的方式:从光源发出,经具有特定材质属性的几何对象反射或折射,最终显示在观察者的眼中,通常是在摄影机的胶片上。为了最大限度地减少计算成本并只渲染场景的可见部分,该算法采用向后计算:它从摄影机处开始,沿着当前视图方向发送光线。如果该光线遇到某个对象,则将对其材质求值,然后返回并存储最终的颜色信息。如果材质能够进行反射或折射,则会将光线进一步发送到场景中以计算对最终颜色的贡献。此过程会递归重复,直到达到特定遍历深度。
- 应用
- 计算反射和折射。
- 通过对点和光源之间是否存在任何对象进行求值计算非常精确的阴影。也可以通过其他方法计算阴影;这些方法虽然速度更快,但精确度较低。
- 光线跟踪能够创建半透明阴影(例如,彩色玻璃的阴影投射)。
辐射度(Radiosity)概念 C398 CG41
Radiosity solves rendering equation for perfectly diffuse surfaces
- 辐射度算法(Radiosity)是一种全局光照算法,用于三维计算机图形学绘制。和倾向于只在一个表面上模拟一次光的反射的直接光照算法(例如光线跟踪)不同,像辐射度算法这样的全局光照算法模拟光在一个场景里的多次反射,通常会导致更柔和更自然的影子和反射。
- Consider objects to be broken up into flat patches (which may correspond to the polygons in the model)
- Assume that patches are perfectly diffuse reflectors
- Radiosity = flux = energy/unit area/ unit time leaving patch