线性回归——梯度下降法(公式推导和自定义代码实现)
接上一篇文章 线性回归——最小二乘法(公式推导和非调包实现)
前言:
不知不觉已经做了几期的线性回归的算法博文了,写博文就是这样虽说自己经理解了,但是讲出来别人却不一定能够听懂,因为自己写博文肯定是跟着自己的习惯和思路走的,对于读者来说就并不那么好懂.如果你看过博主往期的算法讲解应该会发现博主在证明原理讲解时内容都普遍啰嗦,本来可以一笔带过的地方,可还是会花篇幅去讲解.可能是有强迫症吧,我觉得既然讲一个东西就不能将得似懂非懂,反而误人子弟,能够多一点就多一点吧,不为别人也为自己将来回过头来复习提供便利.博主在上期的文章中讲到了线性回归中的最小二乘法的推导和计算,今天就来说一下梯度下降法吧,有人可能会纳闷,既然都有了最小二乘法可以计算线性回归问题了,为什么还有多来一种梯度下降法呢?其实你观察最小二乘法的公式你就清楚了,最小二乘法只适用于训练数据满秩的情况下才能计算,什么情况是满秩呢?就是你的每行数据中的特征值个数要小于你所有的样本个数.既然是这样那么就来看看梯度下降法是个什么吧:
一、什么是梯度下降?
- 很多初学者一听到这个词就望而生畏,觉得这是一个很高大上的词,觉得很高大上.其实它也只是名字被蒙上了一层面纱,远没有大家想得那么高大上,打个很通俗的比方就是楼梯跟滑滑梯的区别是什么,不就是楼梯是一步一步的移动吗,而滑滑梯则是光滑的持续的运动轨迹,在上面是一瞬即逝的.在打个比方你在一座山上,现在你需要找到一条路下到山底,你现在是不知道下山的路的,山上有很多的岔路口,该怎么办呢?其实解决办法很简单,既然是下山那么你在高度H是必定要减少的,不妨你走一步然后测量一下当前这一步是让你的高度下降了还是上升了.如果是下降了就跟着这个方向走,如果不是则换个方向再测量反复如此,你就到达山下了.这是一个典型的贪心问题,用局部解求出全解的过程.
- 我们再从现实回到书面函数图像上来.
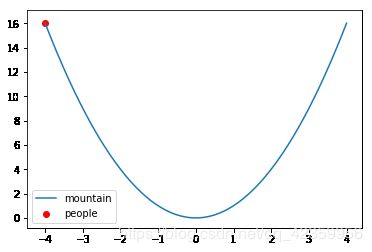
这是一个开口向上的二次函数 f ( x ) = x 2 f(x)=x^2 f(x)=x2 的函数图像,我们把它比作成一座山,它的最低点就是山底,图中还有一个红点,他表示我们人现在所处的位置,如果用梯度下降的方法,让人下山,那么它的轨迹可以表示成下图:
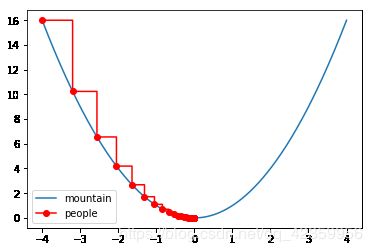
图浅显易懂,一眼便能看出’下山’轨迹,但是问题来了在算法上我们是如何实现的呢?
导数大家都应该清楚吧,导数反应的就是函数中某点的变化率,而且这个变化率是正增长的变化率,换句话说就是某个点它最对应的 f ( x ) f(x) f(x)的增长那个’增脏速度速度’,给他加个负号反转过来便是我们的’下山’方向.在’山路’(函数)中我们么一步就可以用下面的方式来进行表示:
x j = x j − 1 − α f ′ ( x ) x_j=x_{j-1}-\alpha f'(x) xj=xj−1−αf′(x)
其中你发现多另一个 α \alpha α 参数,这个参数的作用是代表我们每一步的跨度,专业术语也叫学习率,之所以要有这个参数是因为,我们要让下上的时间尽量短(也就是一步走大一点),但是也不能太大,如果太大会发生什么呢?请看下图你就明白了:

可以看到在这种函数图像下面,我们如果一步迈大了,那么直接就跳过了最小值的地方,来到了另一个极小值的区域,显然不是我们想要的,所以 α \alpha α 不能太小也不能太大,恰到好处最好
搞懂了原理我们再来根据公式来计算一遍:
我们这里让起点为 x 0 = − 4 x_0=-4 x0=−4, α = 0.4 \alpha=0.4 α=0.4
f ( x ) = x 2 f(x)=x^2 f(x)=x2
f ′ ( x ) = 2 x f'(x)=2x f′(x)=2x
(1):
x 1 = x 0 − α f ′ ( x 0 ) = − 4 − 0.4 × ( 2 × − 4 ) = − 0.8 x_1=x_0-\alpha f'(x_0)\\ =-4-0.4 \times(2\times-4)\\ =-0.8 x1=x0−αf′(x0)=−4−0.4×(2×−4)=−0.8
(2):
x 2 = x 1 − α f ′ ( x 1 ) = − 0.8 − 0.4 × ( 2 × − 0.8 ) = − 0.16 x_2=x_1 -\alpha f'(x_1)\\ =-0.8-0.4\times(2\times-0.8)\\ =-0.16 x2=x1−αf′(x1)=−0.8−0.4×(2×−0.8)=−0.16
(3)
x 3 = x 2 − α f ′ ( x 2 ) = − 0.16 − 0.4 × ( 2 × − 0.16 ) = − 0.032 x_3=x_2 -\alpha f'(x_2)\\ =-0.16-0.4\times(2\times-0.16)\\ =-0.032 x3=x2−αf′(x2)=−0.16−0.4×(2×−0.16)=−0.032
可以看到只经过了三步迭代就已经接近最低点的位置了,可见效率还是挺高.
有了上面的知识你就算入门梯度下降了,你会发现上面只提到了一个自变量的情况,但在实际开发当中数据往往是多维的,具有多个特征值,那么多维的数据该怎么处理呢,上面我们只是提到了导数,其实导数还有一个亲兄弟叫做偏导数,多维度的数据我们往往采用偏导数的方式来解决,如果我们有一个函数是这样的:
f ( θ ) = θ 1 2 + θ 2 2 f(\theta)=\theta_1^2+\theta_2^2 f(θ)=θ12+θ22
通过作图工具我们将图像画出来是这样的:
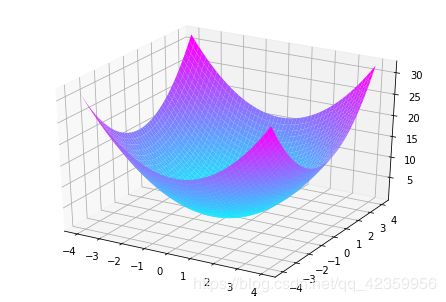
很明显函数的最低点在(0,0,0)处,但我们要怎么来求?先别急计算的原理都是大同小异,在计算之前先了解这样一个概念
在只有一个自变量的函数中我们对其求导,因为只有一个自变量所以它的方向就要么向前,要么向后我们就用一个标量 Δ \Delta Δ
来表示它的变化, Δ \Delta Δ为负表示向后, Δ \Delta Δ为正表示向前.
现在到了有多个自变量的函数中,我们就需要对所有的自变量求一次偏导,然后让这些求得的偏导组成一个列表,我们通常称这个列表为一个向量,向量是具有方向的而标量则没有.求出来的向量是这样的
< δ ( f ( θ ) ) δ θ 1 , δ ( f ( θ ) ) δ θ 1 , ⋯ , δ ( f ( θ ) ) δ θ n > \left<\frac{\delta(f(\theta))}{\delta\theta_1},\frac{\delta(f(\theta))}{\delta\theta_1},\cdots,\frac{\delta(f(\theta))}{\delta\theta_n}\right> ⟨δθ1δ(f(θ)),δθ1δ(f(θ)),⋯,δθnδ(f(θ))⟩
我们不妨来对 f ( θ ) = θ 1 2 + θ 2 2 f(\theta)=\theta_1^2+\theta_2^2 f(θ)=θ12+θ22,这个曲面方程来计算一下它的梯度下降过程:
还以一样先确定取初始位置,起点就设为 < θ 01 , θ 02 > = < 4 , 4 > <\theta_{01},\theta_{02}>=<4,4> <θ01,θ02>=<4,4>, α = 0.4 \alpha=0.4 α=0.4
再分别把偏导函数求出来:
δ ( f ( θ ) ) δ θ 1 = 2 θ 1 , δ ( f ( θ ) ) δ θ 2 = 2 θ 2 \displaystyle \frac{\delta(f(\theta))}{\delta\theta_1}=2\theta_1,\displaystyle \frac{\delta(f(\theta))}{\delta\theta_2}=2\theta_2 δθ1δ(f(θ))=2θ1,δθ2δ(f(θ))=2θ2
然后开始迭代:
(1)
< θ 11 , θ 12 > = < θ 01 − α δ ( f ( θ 01 ) ) δ θ 1 , θ 02 − α δ ( f ( θ 02 ) ) δ θ 2 > = < 4 − 0.4 × ( 2 × 4 ) , 4 − 0.4 × ( 2 × 4 ) > = < 0.8 , 0.8 > <\displaystyle \theta_{11},\theta_{12}>=\left<\theta_{01}-\alpha\displaystyle \frac{\delta(f(\theta_{01}))}{\delta\theta_1},\theta_{02}-\alpha\displaystyle \frac{\delta(f(\theta_{02}))}{\delta\theta_2}\right> \\=<4-0.4\times(2\times4),4-0.4\times(2\times4)> \\=<0.8,0.8> <θ11,θ12>=⟨θ01−αδθ1δ(f(θ01)),θ02−αδθ2δ(f(θ02))⟩=<4−0.4×(2×4),4−0.4×(2×4)>=<0.8,0.8>
(2)
< θ 21 , θ 22 > = < θ 11 − α δ ( f ( θ 11 ) ) δ θ 1 , θ 12 − α δ ( f ( θ 12 ) ) δ θ 2 > = < 0.8 − 0.4 × ( 2 × 0.8 ) , 0.8 − 0.4 × ( 2 × 0.8 ) > = < 0.16 , 0.16 > <\displaystyle \theta_{21},\theta_{22}>=\left<\theta_{11}-\alpha\displaystyle \frac{\delta(f(\theta_{11}))}{\delta\theta_1},\theta_{12}-\alpha\displaystyle \frac{\delta(f(\theta_{12}))}{\delta\theta_2}\right> \\=<0.8-0.4\times(2\times0.8),0.8-0.4\times(2\times0.8)> \\=<0.16,0.16> <θ21,θ22>=⟨θ11−αδθ1δ(f(θ11)),θ12−αδθ2δ(f(θ12))⟩=<0.8−0.4×(2×0.8),0.8−0.4×(2×0.8)>=<0.16,0.16>
(3)
< θ 31 , θ 32 > = < θ 21 − α δ ( f ( θ 21 ) ) δ θ 1 , θ 22 − α δ ( f ( θ 22 ) ) δ θ 2 > = < 0.16 − 0.4 × ( 2 × 0.16 ) , 0.16 − 0.4 × ( 2 × 0.16 ) > = < 0.032 , 0.032 > <\displaystyle \theta_{31},\theta_{32}>=\left<\theta_{21}-\alpha\displaystyle \frac{\delta(f(\theta_{21}))}{\delta\theta_1},\theta_{22}-\alpha\displaystyle \frac{\delta(f(\theta_{22}))}{\delta\theta_2}\right> \\=<0.16-0.4\times(2\times0.16),0.16-0.4\times(2\times0.16)> \\=<0.032,0.032> <θ31,θ32>=⟨θ21−αδθ1δ(f(θ21)),θ22−αδθ2δ(f(θ22))⟩=<0.16−0.4×(2×0.16),0.16−0.4×(2×0.16)>=<0.032,0.032>
……,……
(j)
< θ j 1 , θ j 2 > = < θ ( j − 1 ) 1 − α δ ( f ( θ ( j − 1 ) 1 ) ) δ θ 1 , θ ( j − 1 ) 2 − α δ ( f ( θ ( j − 1 ) 2 ) ) δ θ 2 > <\displaystyle \theta_{j1},\theta_{j2}>=\left<\theta_{(j-1)1}-\alpha\displaystyle \frac{\delta(f(\theta_{(j-1)1}))}{\delta\theta_1},\theta_{(j-1)2}-\alpha\displaystyle \frac{\delta(f(\theta_{(j-1)2}))}{\delta\theta_2}\right> <θj1,θj2>=⟨θ(j−1)1−αδθ1δ(f(θ(j−1)1)),θ(j−1)2−αδθ2δ(f(θ(j−1)2))⟩
由于篇幅原因这里就列出了三次迭代过程,我们来看看将整个过程在途中绘制出来是怎样的

根据图像还是很直观可以看到梯度下降法的下降轨迹.
二、线性回归梯度下降法公式推导
- 最小二乘法公式:
J ( θ ) = 1 2 ∑ i = 1 n ( y i − θ T x i ) 2 J(\theta)=\displaystyle \frac{1}{2}\sum_{i=1}^n{(y_i-\theta^Tx_i)^2} J(θ)=21i=1∑n(yi−θTxi)2
公式的证明与推导在上一篇博文中已经讲解,这里就不阐述公式的由来了,如有疑问可以翻看博文查看由来.为什么要在这里提及最小二乘法的公式呢?这是因为我们这里要引入一个新的式子,均方误差或者也可以叫它代价函数( J ( θ ) J(\theta) J(θ)):
{ J ( θ ) = 1 2 n ∑ i = 1 n ( h θ ( x i ) − y i ) 2 h θ ( x i ) = θ T x i \begin{cases}J(\theta)=\displaystyle \frac{1}{2n}\sum_{i=1}^n{(h_{\theta}(x_i)-y_i})^2\\ h_{\theta}(x_i)=\theta^Tx_i\end{cases} ⎩⎪⎨⎪⎧J(θ)=2n1i=1∑n(hθ(xi)−yi)2hθ(xi)=θTxi
可以看到这个公式和上面的最小二乘法的公式区别就在与前面对整个计算结果除以了一下样本个数,就相当于是求了一下误差的平均值,从而消除了样本个数对参数求解的影响.
让我们来对这个函数求偏导数就有:
δ ( J ( θ ) ) δ ( θ j ) = − 1 n ∑ i = 1 n [ ( h θ ( x i ) − y i ) x i j ] \displaystyle \frac{\delta(J(\theta))}{\delta(\theta_j)}=\frac{-1}{n}\sum_{i=1}^n{[(h_{\theta}(x_i)-y_i)x_{ij}]} δ(θj)δ(J(θ))=n−1i=1∑n[(hθ(xi)−yi)xij]
#################################### 明白求导过程的小伙伴可以跳过 ####################################
到这里的小伙伴肯定会问求导之后为什么会是这样,不妨听博主推导一遍:
在推导之前你要先明白下面三个个性质:
性质一:(复合函数求导公式)
u = x 2 , f ′ ( u ) = f ′ ( u ) u ′ u=x^2,f'(u)=f'(u)u' u=x2,f′(u)=f′(u)u′
性质二:(求偏导时忽略其他自变量)
f ( θ ) = θ 1 2 + 2 θ 2 + θ 3 2 δ ( f ( θ ) ) θ 1 = 2 θ 1 , δ ( f ( θ ) ) θ 2 = 2 , δ ( f ( θ ) ) θ 1 = 2 θ 3 \displaystyle f(\theta)=\theta_1^2+2\theta_2+\theta_3^2\\ \frac{\delta(f(\theta))}{\theta_1}=2\theta_1,\frac{\delta(f(\theta))}{\theta_2}=2,\frac{\delta(f(\theta))}{\theta_1}=2\theta_3 f(θ)=θ12+2θ2+θ32θ1δ(f(θ))=2θ1,θ2δ(f(θ))=2,θ1δ(f(θ))=2θ3
性质三:(导数的加法分配率)
f ( x ) = f 1 ( x ) + f 2 ( x ) , f ′ ( x ) = f 1 ′ ( x ) + f 2 ′ ( x ) f(x)=f_1(x)+f_2(x),f'(x)=f_1'(x)+f_2'(x) f(x)=f1(x)+f2(x),f′(x)=f1′(x)+f2′(x)
明白了这三个性质,我们现在将 J ( θ ) J(\theta) J(θ)展开:
J ( θ ) = ( h θ ( x 1 ) − y 1 ) 2 + ⋯ + ( h θ ( x n ) − y n ) 2 2 n \displaystyle J(\theta)=\frac{(h_\theta(x_1)-y_1)^2+\cdots+(h_\theta(x_n)-y_n)^2}{2n} J(θ)=2n(hθ(x1)−y1)2+⋯+(hθ(xn)−yn)2
开始对 J ( θ ) J(\theta) J(θ)求 θ 0 \theta_0 θ0的偏导数
δ ( J ( θ ) ) δ θ 0 = − 2 ( h θ ( x 1 ) − y 1 ) h θ ′ ( x 1 ) − ⋯ − 2 ( h θ ( x n ) − y n ) h θ ′ ( x 1 ) 2 n \displaystyle \displaystyle \frac{\delta(J(\theta))}{\delta\theta_0}=\frac{-2(h_\theta(x_1)-y_1)h_\theta'(x_1)-\cdots-2(h_\theta(x_n)-y_n)h_\theta'(x_1)}{2n} δθ0δ(J(θ))=2n−2(hθ(x1)−y1)hθ′(x1)−⋯−2(hθ(xn)−yn)hθ′(x1)
把所有的 2 与分母约掉:
δ ( J ( θ ) ) δ θ 0 = − ( h θ ( x 1 ) − y 1 ) δ ( h θ ( x 1 ) ) δ θ 0 − ⋯ − ( h θ ( x n ) − y n ) δ ( h θ ( x n ) ) δ θ 0 n \displaystyle \displaystyle \frac{\delta(J(\theta))}{\delta\theta_0}=\frac{-(h_\theta(x_1)-y_1)\frac{\delta(h_\theta(x_1))}{\delta\theta_0}-\cdots-(h_\theta(x_n)-y_n)\frac{\delta(h_\theta(x_n))}{\delta\theta_0}}{n} δθ0δ(J(θ))=n−(hθ(x1)−y1)δθ0δ(hθ(x1))−⋯−(hθ(xn)−yn)δθ0δ(hθ(xn))
现在我们来计算 δ ( h θ ( x n ) ) δ θ 0 \displaystyle \frac{\delta(h_\theta(x_n))}{\delta\theta_0} δθ0δ(hθ(xn)),先展开再根据性质二可得:
δ ( h θ ( x n ) ) δ θ 0 = δ ( θ 0 x n 0 + θ 0 x n 1 + ⋯ + θ 0 x n m ) δ θ 0 = x n 0 \frac{\delta(h_\theta(x_n))}{\delta\theta_0}=\frac{\delta(\theta_0x_{n0}+\theta_0x_{n1}+\cdots+\theta_0x_{nm})}{\delta\theta_0}=x_{n0} δθ0δ(hθ(xn))=δθ0δ(θ0xn0+θ0xn1+⋯+θ0xnm)=xn0
我们再来回到原来的式子中将 δ ( h θ ( x n ) ) δ θ 0 \frac{\delta(h_\theta(x_n))}{\delta\theta_0} δθ0δ(hθ(xn))替换掉就有:
δ ( J ( θ ) ) δ θ 0 = − ( h θ ( x 1 ) − y 1 ) x 10 − ⋯ − ( h θ ( x n ) − y n ) x n 0 n \displaystyle \displaystyle \frac{\delta(J(\theta))}{\delta\theta_0}=\frac{-(h_\theta(x_1)-y_1)x_{10}-\cdots-(h_\theta(x_n)-y_n)x_{n0}}{n} δθ0δ(J(θ))=n−(hθ(x1)−y1)x10−⋯−(hθ(xn)−yn)xn0
最后将式子合起来表示:
δ ( J ( θ ) ) δ ( θ 0 ) = − 1 n ∑ i = 1 n [ ( h θ ( x i ) − y i ) x i 0 ] \displaystyle \frac{\delta(J(\theta))}{\delta(\theta_0)}=\frac{-1}{n}\sum_{i=1}^n{[(h_{\theta}(x_i)-y_i)x_{i0}]} δ(θ0)δ(J(θ))=n−1i=1∑n[(hθ(xi)−yi)xi0]
############################################# END ################################################
我们求得了偏导函数,现在就可以利用前面所介绍的梯度下降法则了,那么就有公式:
θ j = θ ( j − 1 ) − α 1 n ∑ i = 1 n [ ( h θ ( x i ) − y i ) x i 0 ] \theta_j=\theta_{(j-1)}-\alpha\frac{1}{n}\sum_{i=1}^n{[(h_{\theta}(x_i)-y_i)x_{i0}]} θj=θ(j−1)−αn1i=1∑n[(hθ(xi)−yi)xi0]
这个公式中的 n 代表样本数, α \alpha α代表学习率也就是步长,如果我们每次都取全部样本来计算显然算出来的参数是最准确的,但是时间上肯定也是最大的 n 如果取 1 ,我们随机取一个样本来计算参数,这样是最快,但是准确就不能保证,所以通常n可以取一个常数表示抽取样本中的一部分数据来测试,这样准确率不会太低,时间开销也不会太大.
三、代码实现
- 为了方便计算我们把上面的公式换成矩阵来表式
θ = θ − α 1 n X T ( X θ − Y ) \theta=\theta-\alpha\frac{1}{n}X^T(X\theta-Y) θ=θ−αn1XT(Xθ−Y)
至于为什么可以变成这样,也可以参考博主前面一篇文章中的推理方法,自行推理这里也不多讲了。 - 定义必要的函数:
def error_func(theta,train_x,train_y):
# 均方误差
data_len = train_x.size
temp = np.dot(train_x,theta) - train_y
result = np.dot(temp.T,temp)/2*data_len
return result
def gradient_func(theta,train_x,train_y):
# 梯度
data_len = train_x.size
temp = np.dot(train_x,theta) - train_y
result = np.dot(train_x.T,temp)/data_len
return result
def gradient_descent(x,y,a,valve):
# 根据梯度进行下降
features_len = x.shape[1]
theta = np.ones(features_len).reshape(features_len,1)
data_len = x.shape[0]
while True:
gradient = gradient_func(theta,x,y)
theta = theta - gradient*a
if np.all(np.absolute(gradient) < valve):
return theta
def predict(model,x_data):
# 预测
return np.dot(np.matrix(x_data),model)
- 加载数据训练模型并绘图
from sklearn.datasets import load_boston
boston_data = load_boston().data
X = boston_data[:,:-1]
ones_x = np.ones(X.shape[0])
X = np.column_stack((ones_x,X))
Y = boston_data[:,-1:]
t = gradient_descent(X,Y,0.00004,0.1)
p_y = predict(t,X)
p_y = np.sort(np.array(p_y)[:,0])
plt.scatter(np.arange(0,506),np.sort(boston_data[:,-1]),marker="x",c="r",label="label_data")
plt.plot(np.arange(0,506),p_y,label="predict_data")
plt.legend()
