简单易懂的人工智能系列:模型选择与评估
机器学习过程中需要从假设空间中(众多模型中)选择最优的假设(最优模型)。那么再模型选择过程中(学习过程)必不可少一些选择标准和评估方法,本文就来捋一捋。
模型相关概念
各种误差
误差(Error):是模型的预测输出值与其真实值之间的差异 ,与错误(mistake)(错误是指由于不遵守测量仪器的使用规则,或读取、记录测量结果时粗心等原因造成的。)不同。
训练(Training):通过已知的样本数据进行学习,从而得到模型的过程。
训练误差(Training Error):模型作用于训练集时的误差。
泛化(Generalize):由具体的、个别的扩大为一般的,即从特殊到一般的,称为泛化。对机器学习的的模型来讲,泛化是指模型作用于新的样本数据(非训练集)。
泛化误差(Generalize Error):模型作用于全局样本数据时的误差。
各个概念之间的关系大致如下:
欠拟合和过拟合
模型容量(Model Capacity):是指其拟合各种模型的能力。
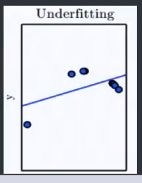
过拟合(Overfitting):是某个模型在训练集上表现的很好,但是到新样本熵表现差。模型将训练集的特征学习的太好,导致一些非普遍规律被模型接纳和体现,从而在训练集上表现好但是对于新样本的表现差。反之则称为欠拟合(Underfitting),即模型对训练集的一般性质学习较差,模型作用于训练集时表现不好。
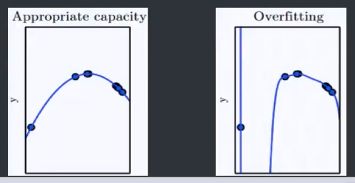
对于同一个训练数据集,下面分别展示了欠拟合,适拟合,过拟合的情况(模型复杂度不断增大,过拟合的模型,学习到了训练数据特有的全局数据却没有的特征)
模型选择
模型选择(Model Selection):针对某个具体的任务,通常会有多种模型(假设空间)可供选择,对同一个模型也会有多组参数,通过分析、评估模型的泛化误差,选择泛化误差最小的模型。
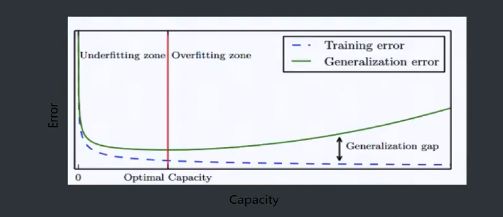
蓝色虚线是模型的训练误差,随着模型容量的增大,不断减小。
绿色实线是模型的泛化误差,随着模型容量先下降后增大。红线为合适区域,两侧分别为欠拟合和过拟合区域。
模型评估思路
通过实验测试,对模型的泛化误差进行评估,选出泛化误差最小的模型。待测数据集全集未知,使用测试集进行泛化测试,测试误差(Testing Errror)即为泛化误差的近似。
测试集和训练集应该满足的条件:
数据集划分方法
留出法(Hold-out)
留出法(Hold-out):将已知的数据集分成两个互斥的部分,其中一部分用来训练模型;另一部分用来测试模型,评估其误差,作为泛化误差的估计。
- 两个数据集的的划分尽可能保证数据分布的一致性,避免因为数据划分过程引入认为的偏差
比如下图的总数据集(男女比例)应该和测试集、训练集(男女比例)相近:
为此(保持类别比例相似),采用分层采样(Stratified Sampleing)
- 数据分割存在多种形式会导致不同的训练集、测试集划分,单次留出法结果往往存在偶然性,其稳定性比较差,通常会进行若干次随机划分,重复试验评估区平均值作为评估结果。
- 数据集拆成两部分,每部分的规模设置会影响评估结果,测试、训练的比例通常为7:3、8:2等。
适用场景:
交叉验证法(Cross Validation)
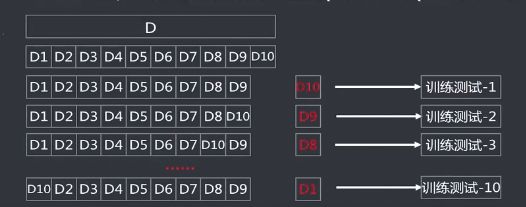
交叉验证法(Cross Validation):将数据集划分 k 个大小相似的互斥的数据子集,子集数据尽可能保证数据分布的一致性(分层采样),每次从中选取一个数据集作为测试集,其余用作训练集,可以进行k次训练和测试,得到评估均值。该验证方法也称作 k 折交叉验证(k-fold Cross Validation)。使用不同的划分,重复 p 次,称为 p 次 k 折交叉验证
比如上图,我们可以将数据集分为 10分,每次选择不同的 一份作为测试集,其余9份作为训练集,进行10次训练,这就是10-折交叉验证,若再改变数据集划分方式,再重复一次,就叫 2 次 10-折交叉验证。
适用场景:
留一法(Leave-One-Out,LOO)
留一法(Leave-One-Out,LOO):是 k 折交叉验证的特殊形式,将数据集划分成两个,其中一个数据集的记录条数为1,做测试集,其余为训练集。训练出的模型和使用全部数据集训练的到的模型接近,其评估结果比较准确。确定是当数据集较大时候,训练次数和计算规模较大。
适用场景:
自助法(Bootstraping)
自助法(Bootstraping):是一种产生样本的抽样方法,其实质是有放回的随机抽样。即从已知数据集中随机抽取一条记录,然后该纪录放入训练集同时也放回原数据集,继续下一次抽样,直到测试集中数据条数满足要求。
假设一只数据集含有n条,采用自助法得到一个记录数为n 的训练集Tran_data。D中的一些数据会在T中重复出现多次,还有部分数据集不会出现,我们可以估算一下经过n次有放回抽样后,大概多少记录未被选中:
说明通过有放回的抽样获得的测试集去训练模型,不在训练集中的数据(总数量的1/3多)用于测试,这样的测试结果被称作包外估计(Out - of - Bag Estimate,OOB),缺点是会使得重复记录的权重加大的偏差。
适用场景:
方法的选择
还有很多其它的衍生方法,我们首先重要的是要掌握这些核心的方法。
模型性能度量
性能度量(Performance Measure):评价模型泛化能力的标准。对于不同的模型,有不同的评价标准,不同的评价标准导致的结果往往也不同。模型的好坏往往也是相对的,取决于对于当前的任务需求完成的效果。
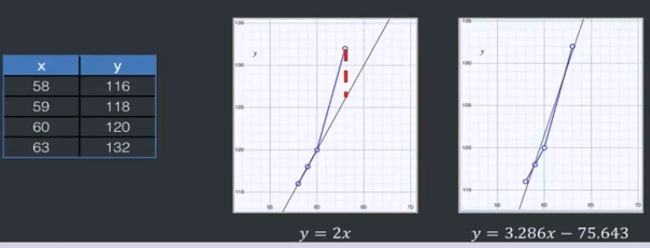
回归模型的性能度量通常采用均方误差(Mean Square Error):
显然第二个模型的性能更好。
分类算法的性能度量
对于各种性能度量,和所应用的任务场景的不同,依据需求进行选择(有时候某种性能度量好并不适合当前的应用任务需求。)
聚类算法的性能度量
模型比较
选择合适的评估方法和相应的性能度量,计算出性能度量后直接比较。
存在以下问题:
把上述问题按照统计学的知识描述一下:
我们来看下面这个掷硬币的问题:
在硬币没有问题的情况下,投掷结果符合 p= 0.5的二项分布:![]()
就会有以下的概率计算结果:
从以上结果判断,通常认为一个事件发生的概率小于5%(0.05-显著性水平),就说明不太可能发生,这里的0.05随着任务要求的严格程度不同,可以取更小的值,比如0.01。