深度学习笔记整理2 - 感知器算法
深度学习
基本概念
- 深度学习是机器学习算法中的一类,其源于人工神经网络的研究。
- 深度学习广泛应用在计算机视觉,音频处理,自然语言处理等诸多领域。
- 深度可以理解为数据计算转换的层数。
机器学习&深度学习
深度学习可以看做是机器学习的一个研究领域(没有严格的定义)。目前,机器学习主要处理结构化数据,而深度学习主要处理非结构化数据。
神经元
深度学习从生物学中受到启发,其灵感来自于人脑的神经网络。 神经网络可以看做是由若干神经元构成。
神经元是大脑中相互连接的神经细胞。其可以处理和传递化学与电信号。
其中,树突用来接收信号(可能包含多个信号),如果累加的信号超过一定的阈值,经过细胞体的整合,就会生成一个输出信号,经过轴突传递给下一个神经元。也就是说,如果输入的信号超过一定的阈值,我们就可以认为神经元被激活,否则,我们可以认为神经元被抑制。
感知器
算法说明
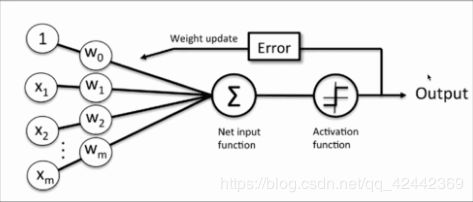
1957年,美国学者Frank Rossenblatt(弗兰克·罗森布拉特)提出了感知器(感知机)算法。感知器用来接收多个信号,输出一个信号(由多个神经元组成)。每个输入信号具有一定的权重,计算多个输入信号的值与权重的乘积和,根据该结果(和)与指定的阈值进行比较,来决定该神经元是否被激活。
说明:
- 感知器是神经网络起源的算法,该思想对于学习神经网络是非常具有指导意义的。
算法公式
根据感知器的定义可知,感知器可以实现二分类的任务。感知器的计算方式如下:

其中,z称为净输入(net input)。然而,这样的计算结果是一个连续的值,我们需要将结果转换为离散的分类值,因此,这里,我们使用一个转换函数,该函数称为激励函数(激活函数)。
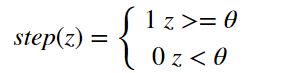
这里, θ \theta θ就是阈值。
说明:
- 我们可以对阈值 θ \theta θ进行调整,使得阈值为0。
- 激活的条件,是>与<=,还是>=与小于,没有明确的要求,二者都可以。
权重更新
感知器是一个自学习算法,即可以根据输入的数据(样本),不断调整权重的更新,最终完成分类。权重的更新公式如下:
w j = w j + Δ w j w_{j} = w_{j} + \Delta w_{j} wj=wj+Δwj
Δ w j = η ( y ( i ) − y ^ ( i ) ) x j ( i ) \Delta w_{j} = \eta (y ^ {(i)} - \hat{y} ^ {(i)}) x_{j}^{(i)} Δwj=η(y(i)−y^(i))xj(i)
其中,j表示某一列,i表示某一个样本。
更新原则
感知器的权重更新依据是:如果预测准确,则权重不进行更新,否则,增加权重,使其更趋向于正确的类别。
实现步骤
- 对权重进行初始化。(初始化为0或者很小的数值。)
- 对训练集中每一个样本进行迭代,计算输出值y。
- 根据输出值y与真实值,更新权重。
- 循环步骤2。直到达到指定的次数(或者完全收敛)。
说明:
- 如果两个类别线性可分,则感知器一定会收敛。
- 如果两个类别线性不可分,则感知器一定不会收敛。
程序示例
使用感知器实现与门与或门的计算。
与门
| b | x1 | x2 | y |
|---|---|---|---|
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
或门
| b | x1 | x2 | y |
|---|---|---|---|
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
练习
- 对上例使用不同的初始化权重,会得到什么结果?
import numpy as np
X = np.array([[1, 0, 0], [1, 0, 1], [1, 1, 0], [1, 1, 1]])
# y = np.array([0, 0, 0, 1])
y = np.array([0, 1, 1, 0])
# w = np.zeros(3)
w = np.random.random(3)
eta = 0.1
for i in range(30):
index = i % 4
z = np.dot(X[index], w)
y_hat = np.where(z >= 0, 1, 0)
print(i + 1, y_hat, y[index], sep="***")
w += eta * (y[index] - y_hat) * X[index]
display(w)
感知器的局限
尝试使用感知器实现异或门,会得到怎样的结果。
| b | x1 | x2 | y |
|---|---|---|---|
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
算法的Python实现
现在,我们使用Python语言来实现感知器算法,进行鸢尾花的分类。
import numpy as np
import pandas as pd
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
# 返回一个元组,进行元组拆包。
X, y = load_iris(return_X_y=True)
# 合并X与y。注意,在合并的时候,需要将y转换为二维数组。
data = pd.DataFrame(np.concatenate((X, y.reshape(len(y), -1)), axis=1))
# 鸢尾花数据集存在重复的记录,删除。
data.drop_duplicates(inplace=True)
len(data)
# 之所以映射为1与-1,是为了与感知器预测的值相符。
data[4] = data[4].map({0:1, 1:-1, 2:2})
# 将类别为2的鸢尾花数据过滤。
data = data[data[4] != 2]
# data.shape
class Perceptron:
"""使用Python语言实现感知器。进行二分类。"""
def __init__(self, alpha, times):
"""初始化方法。
Parameters
-----
alpha : float
学习率。
times : int
最大迭代次数。
"""
self.alpha = alpha
self.times = times
def step(self, z):
"""阶跃函数。
Parameters
-----
z : 数组类型(或标量类型)。
阶跃函数的参数。即感知器的净输入。
Returns
-----
value : int
如果z >= 0,返回1,否则返回-1。
"""
return np.where(z >= 0, 1, -1)
def fit(self, X, y):
"""根据提供的训练数据,对模型进行训练。
Parameters
-----
X : 类数组类型。形状为[样本数量, 特征数量]
待训练的样本特征属性。
y : 类数组类型,形状为[样本数量]
每个样本的目标值(标签)。
"""
X = np.asarray(X)
y = np.asarray(y)
# 创建权重的向量,初始值为0,长度比特征数多1。(多出的一个值是截距)
self.w_ = np.zeros(1 + X.shape[1])
# 创建损失列表,用来保存每次迭代后的损失值。
self.loss_ = []
# 循环指定的次数。
for i in range(self.times):
# 定义每次循环的损失值,即预测错误的数量。
loss = 0
# 依次获取训练集中的每个样本(特征x与目标标签y)。
for x, target in zip(X, y):
# 计算预测值。
y_hat = self.step(np.dot(x, self.w_[1:]) + self.w_[0])
# 如果预测值与真实值不符,则增加误差。
loss += y_hat != target
# 计算更新的梯度值。计算方式为:δw(j) = 学习率 * (真实目标值 - 预测值) * x(j)
# w += δw
# 对权重进行更新。
self.w_[0] += self.alpha * (target - y_hat)
self.w_[1:] += self.alpha * (target - y_hat) * x
# 将循环中累计的误差增加到误差列表中。
self.loss_.append(loss)
def predict(self, X):
"""根据参数传递的样本,对样本数据进行预测。
Parameters
-----
X : 类数组类型,形状为[样本数量, 特征数量]
待测试的样本特征(属性)
Returns
-----
result : 数组类型。
预测的结果(分类值)。
"""
return self.step(np.dot(X, self.w_[1:]) + self.w_[0])
X, y = data.iloc[:, 0:4], data[4]
train_X, test_X, train_y, test_y = train_test_split(X, y, test_size=0.2, random_state=0)
p = Perceptron(0.1, 10)
p.fit(train_X, train_y)
result = p.predict(test_X)
display(result)
display(test_y.values)
display(p.w_)
display(p.loss_)
display(np.sum(result == test_y) / len(result))
import matplotlib as mpl
import matplotlib.pyplot as plt
# 设置字体为黑体,进而可以正常显示中文。
mpl.rcParams["font.family"] = "SimHei"
# 设置在中文字体时,能够正常显示负号。
mpl.rcParams["axes.unicode_minus"]=False
# 绘制真实值
plt.plot(test_y.values, "go", ms=15, label="真实值")
# 绘制预测值.
plt.plot(result, "rx", ms=15, label="预测值")
plt.title("感知器二分类")
plt.xlabel("样本序号")
plt.ylabel("类别")
plt.legend()
plt.show()
# 绘制目标函数损失值
plt.plot(range(1, p.times + 1), p.loss_, "o-")
练习
- 使用感知器对鸢尾花的后两个类别进行分类。
- 使用Python实现train_test_split方法的功能。