传纸条(动态规划)
转自:https://blog.csdn.net/u011077606/article/details/43302987
传纸条(NOIP2008,Vijos-1493)
题目描述:
小渊和小轩是好朋友也是同班同学,他们在一起总有谈不完的话题。一次素质拓展活动中,班上同学安排做成一个m行n列的矩阵,而小渊和小轩被安排在矩阵对角线的两端,因此,他们就无法直接交谈了。幸运的是,他们可以通过传纸条来进行交流。纸条要经由许多同学传到对方手里,小渊坐在矩阵的左上角,坐标(1,1),小轩坐在矩阵的右下角,坐标(m,n)。从小渊传到小轩的纸条只可以向下或者向右传递,从小轩传给小渊的纸条只可以向上或者向左传递。
在活动进行中,小渊希望给小轩传递一张纸条,同时希望小轩给他回复。班里每个同学都可以帮他们传递,但只会帮他们一次,也就是说如果此人在小渊递给小轩纸条的时候帮忙,那么在小轩递给小渊的时候就不会再帮忙。反之亦然。
还有一件事情需要注意,全班每个同学愿意帮忙的好感度有高有低(注意:小渊和小轩的好心程度没有定义,输入时用0表示),可以用一个0-100的自然数来表示,数越大表示越好心。小渊和小轩希望尽可能找好心程度高的同学来帮忙传纸条,即找到来回两条传递路径,使得这两条路径上同学的好心程度只和最大。现在,请你帮助小渊和小轩找到这样的两条路径。
输入格式:
输入第一行有2个用空格隔开的整数m和n,表示班里有m行n列(1<=m,n<=50)。
接下来的m行是一个m*n的矩阵,矩阵中第i行j列的整数表示坐在第i行j列的学生的好心程度。每行的n个整数之间用空格隔开。
输出格式:
输出共一行,包含一个整数,表示来回两条路上参与传递纸条的学生的好心程度之和的最大值。
输入样例:
3 3
0 3 9
2 8 5
5 7 0
输出样例:
34
【算法分析】
本题要求一条从(1,1)到(m,n),再从(m,n)到(1,1)的路径,先来看这道题目的简化版:只求一条从(1,1)到(m,n)的路径,使得路径上的点的和最大。
这道题目里面,最显而易见的变化中的量就是纸条所在的坐标(x,y),用dp[x][y]来表示纸条传到(x,y)这个坐标的时候,最大的好心程度之和,那么:
dp[1][1]=0
dp[x][y]=0 if (x,y)在界外
dp[x][y]=max(dp[x-1][y],dp[x][y-1])+a[x][y] if (x,y)在界内
如此一来,简化版本的题目可以很轻松的解决。虽然题目解决了,但是我们却难以通过这个方程来很好的抽象出动态规划的阶段。为了找到阶段,我们来看这样一个例子:
他们都在一条45度的斜线上,且满足x+y=7。
更普遍的,对于所有步数为s可以到达的坐标,x+y=s+2。所以,我们可以用走的步数来划分阶段,通过不同的步数,把这个题目划分成若干个不同的阶段。最后一个阶段有且仅有一个点:(n,m)。
接下来来看二维的情况:
首先,我们将模型转化一下。题目要求的是一条从(1,1)到(n,m),再从(n,m)回来的路径,我们可以转化一下思路,想象成有两个人要从(1,1)到(n,m)来传纸条,本题只要求最大的价值,与路径的方向无关,因此,这样做的正确性可以保证。
现在来考虑如何表示每一个状态:当只有一个人的时候,状态的表示是dp[x][y],现在人数翻倍,要同时表示两个人的坐标,因此状态方程也变为:dp[x1][y1][x2][y2],表示第一个人在(x1,y1),第二个人在(x2,y2)时候的最大价值。看到这里,不少喜欢小聪明的读者(抱歉作者也是这样)会很迅速的写下状态转移方程:
dp[x1][y1][x2][y2]=min(dp[x1][y1][x2-1][y2],dp[x1][y1][x2][y2-1]…)
共四种情况,表示的是其中某一个人通过一次传纸条到达了现在的位置,而另一个人早已经到达了这里。
这么做看似没有问题,但却忽略了题目上一个很重要的条件:同一个人只能传一次纸条。
例如,对于dp[2][2][3][3],它有可能是从dp[1][1][3][3]走来的,而dp[1][1][3][3]有可能是dp[1][1][2][2]走来。这里面,(2,2)这个坐标既出现在了第一个人的路径里,又出现在第二个人的路径里,显然是不可以的。
之所以会出现这样的错误,是因为我们的状态转移方程在设计的时候,没有考虑到阶段性!两个人的决策总应该是同时进行的,不能够出现我先走一步,你再走一步的情况,这样会导致前面所指出的“跟随”的问题。我们对状态转移方程稍作改动:
dp[x1][y1][x2][y2]=min(dp[x1-1][y1][x2-1][y2],dp[x1-1][y1][x2][y2-1],dp[x1][y1-1][x2-1][y2],dp[x1][y1-1][x2][y2-1])+a[x1][y1]+a[x2][y2]
增加的说明: 因为这个思路是从左上角一直走到右下角,所以决策要么是向下要么是向右,所以,状态转移方程里的决策要么是同时向下,要么是同时向右,要么一个向下,一个向右,自己在草稿纸上画一张草图,模拟一下就会明白坐标是怎么变化的。
以上四个dp数组分别对应了到达(x1,y1,x2,y2)的四种情况。
此时,两个人的决策是同步的,但是还有一个问题没有解决,那就是如何解决路径相交的问题,请看下图:
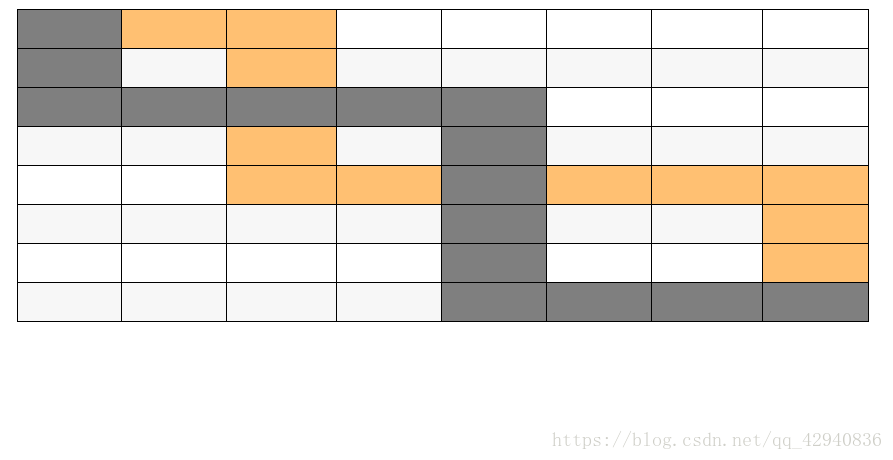
如图所示,这是两条交叉的路径,这在dp的过程中有没有可能出现呢?答案是没有,如果存在着两条交叉的路径,我们可以通过交换交叉的部分,使得他们依旧没有交叉。

此时,就剩下考虑交叉点的问题。题目上要求最大的好心程度之和,又要求路径不能够有相交,但我们的dp过程中,却很难避免相交的问题(如果需要避免,则代码量会增加很多),那么,这种情况是否对答案有影响呢,需要看题目中对数据的描述。
题目中提到:每一个人的好心度都是0~100之间的整数,那么,可以把相交的路径这么更改:

在原来的基础上,路径上又多了两个人,求出来的值必定会>=原来结果。因此,路径上有交叉的情况必然不可能是最后答案,我们完全没有必要在dp的过程中理会路径的交叉情况,只需要在交叉的时候多加这样一句:
if (x1==x2 && y1==y2) dp[x1][y1][x2][y2]-=a[x1][y1];
即可,来避免同一个节点的热心值加了两次。
现在,这道题目已经可以解决,时间和空间复杂度都是O(N4),在题目给定的范围内可以解决。
同样的,利用这样的方法,虽然解决了题目,但是却没有很好的利用阶段的特征。在本题中,我们希望两个人是同时传纸条的,因此,dp[1][1][3][3]这样两个人步数不一致的状态是完全没有用的,我们只关心那些两个人同步决策的状态:dp[x1][y1][x2][y2],且x1+y1=x2+y2。
将上述公式稍微变形:x1+y1-x2=y2。
因此,我们可以把状态压缩成dp[x1][y1][x2],y2直接通过计算得出。
如此一来,时间和空间复杂度都下降到O(N3)。
下面是作者的代码
/*
ID:shijieyywd
PROG:Vijos-1493
LANG:c++
*/
#include 再加上我自己的代码
#include 