大话数据结构----总结一

1.逻辑结构与物理结构
按照视点的不同，我们把数据结构分为逻辑结构和物理结构。
逻辑结构：
逻辑结构是指数据对象中数据元素之间的相互关系。逻辑结构分为以下四种：
集合结构：
集合结构中的数据元素除了同属于一个集合外，它们之间没有其他关系。各个数据元素是“平等的”，它们的共同属性是“同属于一个集合”。
线性结构：
线性结构中的数据元素之间是一对一的关系。
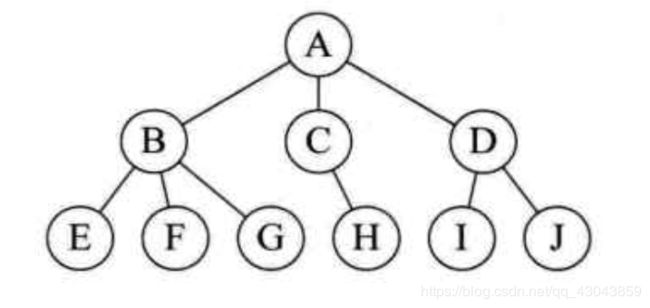
树形结构：
树形结构中的数据元素存在一种一对多的层次关系。

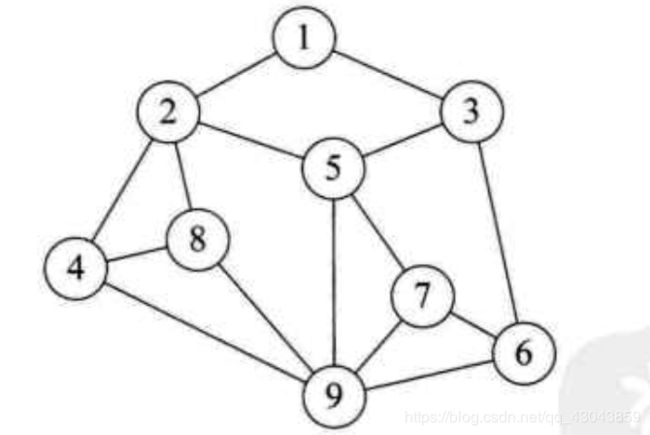
图形结构：
图形结构的数据元素是多对多的关系。

我们在用示意图来表示数据的逻辑结构时，要注意两点：

• 将每一个数据元素看作一个结点，用圆圈表示；
• 元素之间的逻辑关系用结点之间的连线表示，如果这个关系是有方向的，那么用带箭头的连线表示。

物理结构：
物理结构是指数据的逻辑结构在计算机中的存储形式。
数据的存储结构应正确反映数据元素之间的逻辑关系，这才是最为关键的，任何存储数据元素之间的逻辑关系，是实现物理结构的重点和难点。

数据元素的存储结构形式有两种：
顺序存储结构：
顺序存储结构是把数据元素存放在地址连续的存储单元里，其数据间的逻辑关系和物理关系是一致的。

链式存储结构：
链式存储结构是把数据元素存放在任意的存储单元里，这组存储单元可以是连续的，也可以是不连续的。数据元素的存储关系并不能反映其逻辑关系，因此需要用一个指针存放数据元素的地址，这样通过地址就可以找到相关联数据元素的位置。

显然，链式存储就灵活多了，数据存在哪里不重要，只要有一个指针存放了相应的地址就能找到它了。

2.抽象数据类型
数据类型：
数据类型是指一组性质相同的值的集合及定义在此集合上的一些操作的总称。
在C语言中，按照取值的不同，数据类型可以分为两类：

• 原子类型：是不可以再分解的基本类型，包括整型、实型、字符型等；
• 结构类型：由若干个类型组合而成，是可以再分解的。例如，整型数组是由若干整型数据组成的。

3.算法的特性
算法具有五个基本特性：输入、输出、有穷性、确定性和可行性。

有穷性：指算法在执行有限的步骤之后，自动结束而不会出现无限循环，并且每一个步骤在可接受的时间内完成。
确定性：算法的每一步骤都具有确定的含义，不会出现二义性。算法在一定条件下，只有一条执行路径，相同的输入只能有唯一的输出结果。算法的每个步骤被精确定义而无歧义。
可行性：算法的每一步都必须是可行的，也就是说，每一步都能够通过执行有限次数完成。

4.线性表
线性表（List）：零个或多个数据元素的有限序列。
如果用数学语言来进行定义，可如下：
若将线性表记为（a1，a2，…，ai-1，ai，ai+1，…，an），则表中ai-1领先于ai，ai领先于ai+1，称ai-1是ai的直接前驱元素，ai+1是ai的直接后继元素。当i=1,2，…，n-1时，ai有且仅有一个直接后继，当i=2,3，…，n时，ai有且仅有一个直接前驱。

线性表的顺序存储结构的优缺点：
优点：

• 无须为表示表中元素之间的逻辑关系而增加额外的存储空间；
• 可以快速的存取表中任一位置的元素。

缺点：

• 插入和删除操作需要移动大量元素；
• 当线性表长度变化较大时，难以确定存储空间的容量；
• 造成存储空间的“碎片”。

单链表结构与顺序存储结构优缺点：
存储分配方式：

• 顺序存储结构用一段连续的存储单元依次存储线性表的数据元素；
• 单链表采用链式存储结构，用一组任意的存储单元存放线性表的元素。

时间性能能：
查找：

• 顺序存储结构O（1）；
• 单链表O（n）

插入和删除：

• 顺序存储结构需要平均移动表一半的元素，时间为O（n）；
• 单链表在线出某位置，插入和删除时间仅为O（1）

空间性能：

• 顺序存储结构需要预分配存储空间，分大了浪费，分小了易发生上溢；
• 单链表不需要分配存储空间，只要有就可以分配，元素个数也不受限制。

静态链表优缺点：
优点：
在插入和删除操作时，只需要修改游标，不需要移动元素，从而改进了在顺序存储结构中的插入和删除操作需要移动大量元素的缺点。
缺点：

• 没有解决连续存储分配带来的表长难以确定的问题；
• 失去了顺序存储结构随机存取的特性。

5.栈
栈（stack）是限定仅在表尾进行插入和删除操作的线性表。
我们把允许插入和删除的一端称为栈顶（top），另一端称为栈底（bottom），不含任何数据元素的栈称为空栈。栈又称为后进先出（Last In First Out）的线性表，简称LIFO结构。
理解栈的定义需要注意：
首先它是一个线性表，也就是说，栈元素具有线性关系，只不过它是一种特殊的线性表而已。定义中说是在线性表的末尾进行插入和删除操作，这里末尾是指栈顶，而不是栈底。
它的特殊之处就在于限制了这个线性表的插入和删除位置，它始终只在栈顶进行。这也就使得：栈底是固定的，最先进栈的只能在栈底。

栈的链式存储结构：
栈的链式存储结构检查为链栈。
把栈顶放在单链表的头部，通常对于链栈来说，是不需要头结点的。

对比一下顺序栈与链栈，它们在时间复杂度上是一样的，均为O（1）。对于空间性能，顺序栈需要事先确定一个固定的长度，可能会存在内存空间浪费的问题，但它的优势是存取时定位很方便，而链栈则需要每个元素都有指针域，这同时也增加了一些内存开销，但对于栈的长度无限制。所以，它们的区别和线性表中讨论的一样，如果栈的使用过程中元素变化不可预料，有时很小，有时非常大，那么最好是用链栈，反之，如果它的变化在可控范围内，建议使用顺序栈会更好一些。

6.队列
队列（queue）是只允许在一端进行插入操作，而在另一端进行删除操作的线性表。
队列是一种先进先出（First In First Out）的线性表，简称FIFO。允许插入的一端称为队尾，允许删除的一端称为队头。

循环队列定义：
解决假溢出的办法就是后面满了，就再从头开始，也就是头尾相接的循环。我们把队列的这种头尾相接的顺序存储结构称为循环队列。

7.树
树（Tree）是n（n》0）个结点的有限集。n=0时称为空树。在任意一课非空树中：

• 有且仅有一个特定的称为根（Root）的结点；
• 当n>1时，其余结点可分为m（m>0）个互不相交的有限集T1,T2,…,Tm，其中每一个集合本身又是一棵树，并且称为根的子树（SubTree）。

结点分类：
树的结点包含一个数据结构及若干指向其子树的分支。结点拥有的子树数称为结点的度（Degree），度为0的结点称为叶节点（Leaf）或终端结点；度不为0的结点称为非终端结点或分支结点。除根结点之外，分支结点也称为内部结点。树的度是树内各结点的度的最大值。

树的其他相关概念：
结点的层次（Level）从根开始定义起，根为第一层，根的孩子为第二层。若某结点在第l层，则其子树的根就在第l+1层。树中结点的最大层次称为树的深度（Depth）或高度。

如果将树中结点的各子树看成从左至右是有次序的，不能互换的，则称该树为有序树，否则称为无序树。

充分利用顺序存储和链式存储结构的特点，完全可以实现对树的存储结构的表示。双亲表示法、孩子表示法、孩子兄弟表示法。

二叉树：
二叉树（Binary Tree）是n（n》0）个结点的有限集合，该集合或者为空集（称为空二叉树），或者由一个根结点和两棵互不相交的、分别称为根结点的左子树和右子树的二叉树组成。

满二叉树的特点：

• 叶子只能出现在最下一层，出现在其他层就不可能达成平衡；
• 非叶子结点的度一定是2；
• 在同样深度的二叉树中，满二叉树的结点个数最多，叶子数最多。