文本embedding的算法大汇总
文本embedding的算法大汇总
文章目录
- 文本embedding的算法大汇总
- 一、潜在语义分析(Latent Semantic Analysis)
- 1. 简单介绍
- 2. 基本原理
- 2.1 词-文档矩阵(Occurences Matrix)
- 2.2 SVD 分解
- 2.3 流程
- 3. 模型评价
- 3.1 具体应用
- 3.2 优点
- 3.3 缺点
- 二、神经网络语言模型
- 1. 简单介绍
- 2. 基本原理
- 3. 算法流程
- 三、词向量模型 Word2Vec
- 1. 简单介绍
- 2. CBOW 模型
- 2.1 总体算法流程
- 3. Skip-Gram 模型
- 3.1 总体算法流程
- 4. 模型的优化方法
- 4.1 Hierarchical softmax
- 4.1.1 模型参数的梯度计算
- 4.1.2 基于分层 softmax 的 CBOW 模型
- 4.1.3 基于分层 softmax 的 Skip-Gram 模型
- 4.2 Negative Sampling
- 4.2.1 负采样的方法
- 4.2.2 模型参数的梯度计算
- 4.2.3 基于负采样的 CBOW 模型
- 4.2.4 基于负采样的 Skip-Gram 模型
- 四、GloVe
- 1. 简单介绍
- 2. 基本原理
- 2.1 共现矩阵
- 3. 公式推导
- 五、ELMo
- 1. 简单介绍
- 2. 基本原理
- 2.1 具体步骤
- 3. 模型评价
- 3.1 优点
- 3.2 缺点
- 六、GPT
- 1. 简单介绍
- 2. 模型结构和基本原理
- 2.1 无监督预训练
- 2.2 有监督微调
- 2.3 下游任务的改造:
- 3. 模型评价
- 3.1 优点
- 3.2 缺点
- 七、Bert
- 1. 简单介绍
- 2. 基本原理
- 2.1 Masked Language Model
- 2.2 Next Sentence Representation(NSP)
- 2.3 下游任务的改造
- 3. 模型评价
- 3.1 优点
- 3.2 缺点
- 八、GPT 2.0
- 1. 训练数据集
- 2. 输入表示
- 3. 模型的改进
- 参考资料
- 3. 模型的改进
- 参考资料
一、潜在语义分析(Latent Semantic Analysis)
1. 简单介绍
LSA 是 1988 年 S.T.Dumais 等人提出的一种新的信息检索代数模型,是用于知识获取和展示的计算理论和方法,和传统向量空间模型(vector space model)一样使用向量来表示词(terms)和文档(documents),并通过向量间的关系(如cos)来判断词及文档间的关系。不同的是,LSA 把高维的向量空间模型(VSM)表示中的文档映射到低维的潜在语义空间中,并用这种潜在的语义结构来表示词和文本,达到消除词之间的相关性和简化文本向量实现降维的目的。
原文地址:http://en.wikipedia.org/wiki/Latent_semantic_analysis
2. 基本原理
通过对大量的文本集进行统计分析,从中提取出词语的上下文使用含义。技术上通过 SVD 分解等处理,消除了同义词、多义词的影响,提高了后续处理的精度。
2.1 词-文档矩阵(Occurences Matrix)
LSA 使用词-文档矩阵来描述一个词语是否在一篇文档中。矩阵的行表示词,列表示文档,每一个元素可为该词在文档中的词频或者该词语的 tf-idf(term frequency–inverse document frequency),矩阵的每一行代表该词语的向量表示,每一列代表该文档的向量表示。
2.2 SVD 分解
假设 X 为m*n的矩阵,SVD 就是将 X 分解成 3 个矩阵的乘积:
(1.1) X m , n = U m , k ∗ Σ k , k ∗ V n , k T X_{m,n} = U_{m,k}*\Sigma_{k,k}*V^T_{n,k} \tag{1.1} Xm,n=Um,k∗Σk,k∗Vn,kT(1.1)
不妨设 t i T t^T_i tiT为每第 i i i 个词的向量, d j d_j dj为第 j j j 个文本的向量分解可看成如下的样子:

其中 σ 1 , . . . , σ l \sigma_1, ... , \sigma_l σ1,...,σl 被称作奇异值,而 μ 1 , . . . , μ l \mu_1, ... , \mu_l μ1,...,μl 和 ν 1 , . . . , ν l \nu_1, ... ,\nu_l ν1,...,νl 则叫做左奇异向量和右奇异向量,可以看出原始矩阵中的 t i t_i ti只与 U U U 矩阵的第 i i i 行 t ^ i \hat t_i t^i有关, d j d_j dj只与 V V V 矩阵的第 j j j 列 d ^ j \hat d_j d^j有关,且都由矩阵的所有奇异值所决定。
我们可选取k个最大的奇异值,和它们对应的 U U U 和 V V V 中的向量相乘,则能得到一个 X X X 矩阵的k阶近似,这样就将词向量和文档向量映射到了语义空间,这也是一个从高维空间到低维空间的变换。
2.3 流程
-
统计分析文档和词的集合,构建词-文档矩阵 A。
-
对矩阵A做奇异值分解。
-
对 SVD 分解后得到的矩阵降维。
-
使用降维后的矩阵构建潜在的语义空间。
3. 模型评价
3.1 具体应用
-
比较向量 d ^ i \hat d_i d^i和 d ^ j \hat d_j d^j可以判断文档 i i i 和文档 j j j 的相似度,可用于文档聚类和文档分类。
-
在翻译好的文档上进行训练,可以发现不同语言的相似文档,可用于跨语言检索。
-
比较向量 t ^ i \hat t_i t^i与 t ^ j \hat t_j t^j可以判断词 i i i 和词 j j j 的相似度,可用于同义词、歧义词检测。
-
通过查询映射到语义空间,可进行信息检索。给定一个查询字符串,可计算其在语义空间内和已有文档的相关性。
对原始文档,将文档向量映射到语义空间, d ^ j = Σ k − 1 U k T d j \hat d_j = \Sigma^{-1}_k U^T_k d_j d^j=Σk−1UkTdj,对查询字符串,得到其对应词的向量后,根据公式 q ^ = Σ k − 1 U k T q \hat q = \Sigma^{-1}_k U^T_k q q^=Σk−1UkTq 将其映射到语义空间,再与文档向量进行比较。 -
从语义的角度发现词语的相关性,可用于选择题回答模型(multi choice questions answering model)
3.2 优点
- 低维语义空间可以刻画同义词,同义词会对应着相同或相似的主题。
- 降维可以除去部分噪声的影响,增加特征的鲁棒性。
- 充分利用了冗余的数据。
- 无监督/完全自动化。
- 与语言无关。
3.3 缺点
- 新生成的矩阵难以解释。
- LSA 可以处理向量空间模型无法解决的一义多词(synonymy)问题,但不能解决一词多(polysemy)问题。因为 LSA 将每一个词映射为潜在语义空间中的一个点,也就是说一个词的多个意思在空间中对于的是同一个点,并没有被区分。
- LSA 的概率模型假设文档和词的分布是服从联合正态分布的,但从观测数据来看是服从泊松分布的。因此 LSA 算法的一个改进 PLSA 使用了多项分布,其效果要好于 LSA。
- LSA 具有 Bag-of-words model 的缺点,即在一篇文档或者一个句子中忽略词语的先后顺序。
- SVD 的计算复杂度很高,并且当有新的文档到来时,需重新训练更新模型。
二、神经网络语言模型
1. 简单介绍
用神经网络来训练语言模型的思想最早由百度 IDL (深度学习研究院)的徐伟提出,NNLM(Nerual Network Language Model)是这方面的一个经典模型,具体内容可参考 Bengio 2003年发表在 JMLR上的论文。原文地址:http://jmlr.org/papers/volume3/bengio03a/bengio03a.pdf
相对于传统的语言模型,NNLM 模型使用了低维紧凑的词向量对上文进行表示,这解决了词袋模型带来的数据稀疏、语义鸿沟等问题。显然 NNLM 是一种更好的 n 元语言模型,另一方面在相似的上下文语境中,NNLM 模型可以预测出相似的目标词,而传统模型无法做到这一点。
NNLM 模型直接通过一个神经网络结构对 n 元条件概率进行评估,其基本结构如下:

2. 基本原理
NNLM 的概率函数是:
(2.1) f ( w t , w t − 1 , . . . , w t − n + 2 , w t − n + 1 ) = p ( w t ∣ w 1 t − 1 ) f(w_t,w_{t-1},...,w_{t-n+2},w_{t-n+1})=p(w_t|w^{t-1}_1) \tag{2.1} f(wt,wt−1,...,wt−n+2,wt−n+1)=p(wt∣w1t−1)(2.1)
给定一段序列时,由其前面的 n-1个词预测第 n 个词的概率。其中 w t w_t wt 表示第 t 个词, w 1 t − 1 w_1^{t-1} w1t−1 表示从第一个词到第 t 个词组成的序列,且模型满足:
(2.2) { f ( w t , w t − 1 , . . . , w t − n + 2 , w t − n + 1 ) > 0 ∑ i = 1 V f ( w i , w t − 1 , . . . , w t − n + 2 , w t − n + 1 ) = 1 \begin{cases} f(w_t,w_{t-1},...,w_{t-n+2},w_{t-n+1})>0 \\ \sum^V_{i=1}f(w_i,w_{t-1},...,w_{t-n+2},w_{t-n+1})=1 \end{cases} \tag{2.2} {f(wt,wt−1,...,wt−n+2,wt−n+1)>0∑i=1Vf(wi,wt−1,...,wt−n+2,wt−n+1)=1(2.2)
其中 V 为词汇表的大小,即需要满足通过网络预测的每个词的概率都大于0,且所有词的概率之和为1
3. 算法流程
输入:一系列长度为 n 的文本序列训练集,词向量的维度 M,学习率 η \eta η
输出:每一个词的词向量 x w x_w xw
-
第一步对训练集进行分词得到词汇表,每一个单词对应一个索引 i i i
-
第二步随机初始化所有模型参数和映射矩阵 C ∈ R V ∗ N C\in R^{V*N} C∈RV∗N
-
第三步特征映射,通过映射矩阵 C ∈ R V ∗ M C\in R^{V*M} C∈RV∗M 将每一个词映射成一个特征向量, C ( w i ) ∈ R M C(w_i)\in R^M C(wi)∈RM 表示第 i i i 个词的词向量,然后将得到的词向量拼接成一个 ( n − 1 ) M (n-1)M (n−1)M 维的向量(这里我们定义为 h h h): ( C ( w t − n + 1 ) , . . . , C ( w t − 1 ) ) : = h (C(w_{t-n+1}),...,C(w_{t-1})):=h (C(wt−n+1),...,C(wt−1)):=h
-
第四步计算条件分布概率:通过一个函数 g g g 将输入的词向量序列 h h h 转化成一个概率分布 y ∈ R V y\in R^V y∈RV,其中第 i i i 个元素表示预测的词是第 i i i 个词的概率
(2.3) f ( w i , w t − 1 , . . . , w t − n + 2 , w t − n + 1 ) = g ( w i , h ) f(w_i,w_{t-1},...,w_{t-n+2},w_{t-n+1})=g(w_i,h) \tag{2.3} f(wi,wt−1,...,wt−n+2,wt−n+1)=g(wi,h)(2.3) -
第五步定义神经网络输出层输出:
(2.4) p ( w t ∣ w t − 1 , . . . , w t − n + 2 , w t − n + 1 ) = e x p ( y w t ) ∑ i V e x p ( y w i ) p(w_t|w_{t-1},...,w_{t-n+2},w_{t-n+1})=\frac{exp(y_{w_t})}{\sum^V_iexp(y_{w_i})} \tag{2.4} p(wt∣wt−1,...,wt−n+2,wt−n+1)=∑iVexp(ywi)exp(ywt)(2.4)
其中 y = b + W + U t a n h ( d + H x ) y=b+W+Utanh(d+Hx) y=b+W+Utanh(d+Hx),模型的参数 θ = ( b , d , W , U , H , C ) , x = h \theta=(b,d,W,U,H,C),x=h θ=(b,d,W,U,H,C),x=h 是神经网络的输入。 W ∈ R V ∗ ( n − 1 ) M , H ∈ R Q ∗ ( n − 1 ) M , U ∈ R V ∗ Q W\in R^{V*(n-1)M},H\in R^{Q*(n-1)M},U\in R^{V*Q} W∈RV∗(n−1)M,H∈RQ∗(n−1)M,U∈RV∗Q,其中 W W W 是可选参数, H H H 是输入层到隐藏层的权重矩阵, U U U 是隐藏层到输出层的权重矩阵, d , b d,b d,b 是偏置。 -
第六步定义似然函数并更新参数:
(2.5) L = 1 T ∑ t l o g f ( w t , w t − 1 , . . . , w t − n + 1 ; θ ) + R ( θ ) L=\frac 1T\sum_tlogf(w_t,w_{t-1},...,w_{t-n+1};\theta)+R(\theta) \tag{2.5} L=T1t∑logf(wt,wt−1,...,wt−n+1;θ)+R(θ)(2.5)(2.6) θ ← θ + η ∂ l o g p ( w t ∣ w t − 1 , . . . , w t − n + 1 ) ∂ θ \theta \leftarrow\theta + \eta\frac{\partial logp(w_t|w_{t-1},...,w_{t-n+1})}{\partial \theta} \tag{2.6} θ←θ+η∂θ∂logp(wt∣wt−1,...,wt−n+1)(2.6)
其中 R ( θ ) R(\theta) R(θ) 是正则项
三、词向量模型 Word2Vec
1. 简单介绍
word2vec 模型其实就是一个简单的神经网络,输入层是One-Hot Vector,中间隐藏层没有激活函数,输出层维度和输入层维度一样,用 softmax 回归。这个模型的产物是隐藏层训练好的参数,对应着每一个词的词向量表示。它本质上是一种单词聚类的方法,是实现单词语义推测、句子情感分析等目的一种手段。但是它的 context 窗口很小,没有使用全局的 cooccur,所以实际上对 cooccur 的利用很少。
模型根据输入和输出的定义可分为 CBOW(Continuous Bag-of-Words)与 Skip-Gram 两种模型。CBOW 的输入是某个词的上下文词的词向量,输出是该词的词向量。Skip-Gram 则是与 CBOW 相反,输入是一个词的词向量,输出是该词对应的上下文词的词向量。CBOW 在只适合在少量数据集中训练,而 Skip-Gram 在大型的语料集中表现更好。

2. CBOW 模型
输入层是由上下文的词的 One-hot 编码 { x 1 , . . . , x C } \{x_1, ... , x_C\} {x1,...,xC} 组成,其中窗口大小为C,词汇表大小为V,隐藏层是N维的向量,输出是 One-hot 编码的输出单词 y y y,输入的 One-hot 向量通过一个 V × N 维的权重矩阵 W W W 连接到隐藏层,再通过一个 N × V 的矩阵 W T W^T WT 连接到输出层。
2.1 总体算法流程
输入:语料训练样本,词向量的维度大小 N N N,CBOW 的上下文窗口大小 C C C ,步长 η \eta η
输出:所有词的输入词向量 v v v 和输出词向量 v ′ v' v′,即权重矩阵 W W W 和 W ′ W' W′
-
第一步随机初始化模型参数 W W W 和 W ′ W' W′
-
第二步计算隐藏层 h h h 的输出:
(3.2.1) h = 1 C W T ⋅ ( ∑ i = 1 C x i ) = 1 C ( v w 1 + v w 2 + . . . + v w C ) T h = \frac 1C W^T⋅(\sum^C_{i=1}x_i)=\frac 1C(v_{w_1}+v_{w_2}+...+v_{w_C})^T \tag{3.2.1} h=C1WT⋅(i=1∑Cxi)=C1(vw1+vw2+...+vwC)T(3.2.1) -
第三步计算输出层的输入:
(3.2.2) u = h ⋅ W ′ u=h\cdot W' \tag{3.2.2} u=h⋅W′(3.2.2)
-
第四步计算输出层的输出:
(3.2.3) y c , j = p ( w y , j ∣ w 1 , . . . , w c ) = e x p ( u j ) ∑ j ′ = 1 V e x p ( u j ′ ) y_{c,j} = p(w_{y,j}|w_1,...,w_c) = \frac {exp(u_j)}{\sum^V_{j'=1}exp(u_{j'})} \tag{3.2.3} yc,j=p(wy,j∣w1,...,wc)=∑j′=1Vexp(uj′)exp(uj)(3.2.3)
其中 u j u_j uj是输出 u u u 的第 j j j 个数,即对应的第 j j j 个词的概率。 -
第五步定义损失函数,即为给定上下文的输出单词的条件概率,取对数形式:
(3.2.4) L o s s = − l o g p ( w O ∣ w I ) = − u j o + l o g ∑ j ′ = 1 V e x p ( u j ′ ) Loss = -logp(w_O|w_I) = -u_{j_o} + log\sum^V_{j'=1}exp(u_{j'}) \tag{3.2.4} Loss=−logp(wO∣wI)=−ujo+logj′=1∑Vexp(uj′)(3.2.4)
其中 j o j_o jo是真实输出的词的索引值,我们的目标是最小化 L o s s Loss Loss 。 -
第六步对上述 L o s s Loss Loss 求偏导并更新输出层权重矩阵 $W’ 与隐藏层权重矩阵 $ W W W 直到梯度收敛:
(3.2.5) ∂ l o s s ∂ u j = y c , j − t j : = e j \frac {\partial loss}{\partial u_j}=y_{c,j} - t_j:=e_j \tag{3.2.5} ∂uj∂loss=yc,j−tj:=ej(3.2.5)
其中 t j t_j tj当 j = j o j=j_o j=jo时等于1,其他情况为0 。然后可求出输出层权重的梯度:
(3.2.6) ∂ l o s s ∂ W i j ′ = ∂ l o s s ∂ u j ⋅ ∂ u j ∂ W i j ′ = e j ⋅ h i \frac {\partial loss}{\partial W'_{ij}}=\frac {\partial loss}{\partial u_j}\cdot\frac {\partial u_j}{\partial W'_{ij}}=e_j\cdot h_i \tag{3.2.6} ∂Wij′∂loss=∂uj∂loss⋅∂Wij′∂uj=ej⋅hi(3.2.6)
则输出层权重更新规则如下:
(3.2.7) W i j ′ ( n e w ) = W i j ′ ( o l d ) − η ⋅ e j ⋅ h i W'^{(new)}_{ij}=W'^{(old)}_{ij}-\eta\cdot e_j\cdot h_i \tag{3.2.7} Wij′(new)=Wij′(old)−η⋅ej⋅hi(3.2.7)
或者:
(3.2.8) v w j ′ ( n e w ) = v w j ′ ( o l d ) − η ⋅ e j ⋅ h f o r j = 1 , 2 , . . . , V v'^{(new)}_{w_j}=v'^{(old)}_{w_j}-\eta\cdot e_j\cdot h\qquad for\ j=1,2,...,V \tag{3.2.8} vwj′(new)=vwj′(old)−η⋅ej⋅hfor j=1,2,...,V(3.2.8)
学习率 η > 0 , e j = y c , j − t j , h j \eta>0,e_j=y_{c,j}-t_j,h_j η>0,ej=yc,j−tj,hj是隐藏层的第 j j j 个单元, v w j T v^T_{w_j} vwjT是单词 w j w_j wj 的输出向量同理 W W W 的梯度:
(3.2.9) ∂ l o s s ∂ h i = ∑ j = 1 V ∂ l o s s ∂ u j ⋅ ∂ u j ∂ h i = ∑ j = 1 V e j ⋅ W i j ′ : = E H i \frac {\partial loss}{\partial h_i}=\sum^V_{j=1}\frac {\partial loss}{\partial u_j}\cdot\frac {\partial u_j}{\partial h_i}=\sum^V_{j=1}e_j\cdot W'_{ij}:=EH_i \tag{3.2.9} ∂hi∂loss=j=1∑V∂uj∂loss⋅∂hi∂uj=j=1∑Vej⋅Wij′:=EHi(3.2.9)
又因为
(3.2.10) h i = 1 C ∑ c = 1 C v w c i = 1 C ∑ c = 1 C ∑ k = 1 V x w c k ⋅ W k i h_i = \frac 1C\sum^C_{c=1}v_{w_c}^i=\frac 1C\sum^C_{c=1}\sum^V_{k=1}x_{w_c}^k\cdot W_{ki} \tag{3.2.10} hi=C1c=1∑Cvwci=C1c=1∑Ck=1∑Vxwck⋅Wki(3.2.10)(3.2.11) ∂ l o s s ∂ W k i = ∂ l o s s ∂ h i ∂ h i ∂ W k i = E H i ⋅ 1 C ∑ c = 1 C x w c k \frac {\partial loss}{\partial W_{ki}}=\frac {\partial loss}{\partial h_i}\frac {\partial h_i}{\partial W_{ki}}=EH_i\cdot \frac 1C\sum^C_{c=1}x^k_{w_c} \tag{3.2.11} ∂Wki∂loss=∂hi∂loss∂Wki∂hi=EHi⋅C1c=1∑Cxwck(3.2.11)
其中 x w c k x^k_{w_c} xwck 指的是第c个单词的One-hot向量的第 k k k 个元素的值,所以
(3.2.12) ∂ l o s s ∂ W = ∂ l o s s ∂ h ⋅ ∂ h ∂ W = 1 C x w c ⋅ E H T \frac {\partial loss}{\partial W}=\frac {\partial loss}{\partial h}\cdot\frac {\partial h}{\partial W}=\frac 1Cx_{w_c}\cdot EH^T \tag{3.2.12} ∂W∂loss=∂h∂loss⋅∂W∂h=C1xwc⋅EHT(3.2.12)这里我们得到的是一个 V ∗ N V*N V∗N 维度的矩阵,又因为对每个 x w c x_{w_c} xwc ,都为只有一个元素值为1、其他都为0的One-hot编码,故 ∂ l o s s / ∂ W {\partial loss}/{\partial W} ∂loss/∂W 矩阵中只有 w c w_c wc 单词的索引行不为0,行值为 1 C E H \frac 1CEH C1EH,所以 W W W 的更新公式为:
(3.2.13) v w I , c ( n e w ) = v w I , c ( o l d ) − 1 C ⋅ η ⋅ E H T v^{(new)}_{w_{I,c}}=v^{(old)}_{w_{I,c}}-\frac 1C\cdot\eta\cdot EH^T \tag{3.2.13} vwI,c(new)=vwI,c(old)−C1⋅η⋅EHT(3.2.13)
其中 v w I , c ( n e w ) v^{(new)}_{w_{I,c}} vwI,c(new)是上下文中第c个单词的输入向量(隐藏层权重的对应单词的行向量)
3. Skip-Gram 模型
Skip-Gram模型是由Mikolov等人提出的。上图展示了Skip-Gram模型的过程,该模型可以看作CBOW模型的逆过程。
3.1 总体算法流程
输入:语料训练样本,词向量的维度大小 N N N,需要预测的上下文窗口大小 C C C ,步长 η \eta η
输出:所有词的输入词向量 v v v 和输出词向量 v ′ v' v′,即权重矩阵 W W W 和 W ′ W' W′
-
第一步随机初始化模型参数 W W W 和 W ′ W' W′
-
第二步计算隐藏层 h h h 输出:
(3.3.1) h = W ( k , ⋅ ) : = v w I h=W_{(k,\cdot)}:=v_{w_I} \tag{3.3.1} h=W(k,⋅):=vwI(3.3.1) -
第三步计算输出层的输入:
(3.3.2) u = h ⋅ W ′ u = h\cdot W' \tag{3.3.2} u=h⋅W′(3.3.2) -
第四步计算输出层的输出:
(3.3.3) y c , j = p ( w c , j = w O , c ∣ w I ) = e x p ( u c , j ) ∑ j ′ = 1 V e x p ( u j ′ ) y_{c,j}=p(w_{c,j}=w_{O,c}|w_I)=\frac {exp(u_{c,j})}{\sum^V_{j'=1}exp(u_{j'})} \tag{3.3.3} yc,j=p(wc,j=wO,c∣wI)=∑j′=1Vexp(uj′)exp(uc,j)(3.3.3)
这里 w c , j w_{c,j} wc,j 是第 c c c 个输出, w O , c w_{O,c} wO,c 是中心词对应的目标单词中的第 c c c 个单词, w I w_I wI 是中心词(即输入词), y c , j y_{c,j} yc,j 是第 c c c 个输出向量的第 j j j 个单元的输出值, u c , j u_{c,j} uc,j 是第 c c c 个输出向量上的第 j j j 个单元的输入。且有:
(3.3.4) u c , j = u j = v w j ′ T ⋅ h u_{c,j}=u_j=v'^T_{w_j}\cdot h\tag{3.3.4} uc,j=uj=vwj′T⋅h(3.3.4)
v w j ′ T v'^T_{w_j} vwj′T 是词汇表第 j j j 个单词的输出向量( W ′ W' W′ 的第 j j j 列) -
第五步定义损失函数:
(3.3.5) L o s s = − ∑ c = 1 C u j c ∗ + C ⋅ l o g ∑ j ′ = 1 V e x p ( u j ′ ) Loss=-\sum^C_{c=1}u_{j^*_c}+C\cdot log\sum^V_{j'=1}exp(u_{j'})\tag{3.3.5} Loss=−c=1∑Cujc∗+C⋅logj′=1∑Vexp(uj′)(3.3.5)
其中 j c ∗ j^*_c jc∗ 表示第 c c c 个真实输出单词的索引值 -
第六步对上述 L o s s Loss Loss 求偏导并更新输出层权重矩阵 $W’ 与隐藏层权重矩阵 $ W W W 直到梯度收敛:
(3.3.6) ∂ l o s s ∂ u c , j = y c , j − t c , j : = e c , j \frac {\partial loss}{\partial u_{c,j}}=y_{c,j}-t_{c,j}:=e_{c,j}\tag{3.3.6} ∂uc,j∂loss=yc,j−tc,j:=ec,j(3.3.6)
我们可定义一个 V 维的向量 E I = { E I 1 , . . . , E I V } EI = \{EI_1,...,EI_V\} EI={EI1,...,EIV} ,该向量是 C 个预测单词的误差总和:
(3.3.7) E I j = ∑ c = 1 C e c , j EI_j=\sum^C_{c=1}e_{c,j}\tag{3.3.7} EIj=c=1∑Cec,j(3.3.7)
(3.3.8) ∂ l o s s ∂ W i j ′ = ∑ c = 1 C ∂ l o s s ∂ u c , j ⋅ ∂ u c , j ∂ W i j ′ = E I j ⋅ h i \frac {\partial loss}{\partial W'_{ij}}=\sum^C_{c=1}\frac {\partial loss}{\partial u_{c,j}}\cdot\frac {\partial u_{c,j}}{\partial W'_{ij}}=EI_j\cdot h_i\tag{3.3.8} ∂Wij′∂loss=c=1∑C∂uc,j∂loss⋅∂Wij′∂uc,j=EIj⋅hi(3.3.8)
输出层权重矩阵 W ′ W' W′ 的更新公式:
(3.3.9) W i j ′ ( n e w ) = W i j ′ ( o l d ) − η ⋅ E I j ⋅ h i W'^{(new)}_{ij}=W'^{(old)}_{ij}-\eta\cdot EI_j\cdot h_i\tag{3.3.9} Wij′(new)=Wij′(old)−η⋅EIj⋅hi(3.3.9)
或者
(3.3.10) v w j ′ ( n e w ) = v w j ′ ( o l d ) − η ⋅ E I j ⋅ h v'^{(new)}_{w_j}=v'^{(old)}_{w_j}-\eta\cdot EI_j\cdot h\tag{3.3.10} vwj′(new)=vwj′(old)−η⋅EIj⋅h(3.3.10)
隐藏层权重矩阵 W W W 的更新公式:
(3.3.11) v w I ( n e w ) = v w I ( o l d ) − η ⋅ E H T v^{(new)}_{w_I}=v^{(old)}_{w_I}-\eta\cdot EH^T\tag{3.3.11} vwI(new)=vwI(old)−η⋅EHT(3.3.11)
其中 E H EH EH 是一个N维向量
(3.3.12) E H i = ∑ j = 1 V E I j ⋅ W i j ′ EH_i=\sum^V_{j=1}EI_j\cdot W'_{ij}\tag{3.3.12} EHi=j=1∑VEIj⋅Wij′(3.3.12)
4. 模型的优化方法
对上述模型,每个单词都存在两类向量的表达,即输入向量 v w v_w vw(输入层到隐藏层的权重矩阵 W W W),输出向量 v w ′ v'_w vw′(隐藏层到输出层的权重矩阵 W ′ W' W′)。学习得到输入向量比较简单,但是学习输出向量是很困难的,需要遍历词汇表中的每个单词。若词汇表非常巨大,那么计算是非常庞大的。
为了解决计算量太大的问题,我们有两种改进的优化方法:分层 softmax(Hierarchical softmax)和负采样(negative sampling)。
4.1 Hierarchical softmax
为了避免计算词汇表所有词的 softmax 概率,分层 softmax 采用霍夫曼树(huffman)来代替隐藏层到输出 softmax 层的映射。即将上述的输出层权重矩阵 W ′ W' W′ 替换成 霍夫曼树的隐节点的权重 θ \theta θ 。
由于霍夫曼树是二叉树,故计算量由之前的 V 变成 l o g 2 V log_2V log2V,而且我们仍然有差不多同样的模型参数(原始模型:V 个单词的输出向量,分层 softmax:V - 1 个隐节点的输出向量)。且依据每个单词的词频作为权重构建的霍夫曼树,高频词的路径更短,更容易被找到。
这里树的所有内部节点就类似之前的神经网络隐藏层的神经元。根节点的词向量对应我们投影后的词向量,而所有叶子节点就类似之前 softmax 输出层的神经元,叶子节点的个数就是词汇表的大小。这里从隐藏层到输出层的 softmax 映射不是一下就完成的,是沿着霍夫曼树一步一步完成的。每一个隐节点都是一个二分类的逻辑回归问题,往左子树走为负类(霍夫曼编码为1),右边则为正类(编码为0),激活函数用 sigmoid 函数即:
(3.4.1) P ( + ) = σ ( x w T θ ) = 1 1 + e x p ( − x w T θ ) P(+)=\sigma(x^T_w\theta)=\frac 1{1+exp(-x^T_w\theta)}\tag{3.4.1} P(+)=σ(xwTθ)=1+exp(−xwTθ)1(3.4.1)
其中 x w x_w xw 是当前内部节点的词向量, θ \theta θ 是我们需要训练得到的模型参数
4.1.1 模型参数的梯度计算
分层 softmax 没有单词的输出向量,而是 V - 1 个隐节点都有一个输出向量 v n ( w , j ) ′ v'_{n(w,j)} vn(w,j)′ 。首先定义经过霍夫曼树某一个节点 j j j 的逻辑回归概率:
(3.4.2) P ( d j w ∣ x w , θ j − 1 w ) = { σ ( x w T θ j − 1 w ) d j w = 0 1 − σ ( x w T θ j − 1 w ) d j w = 1 P(d^w_j|x_w,\theta^w_{j-1})= \begin{cases} \sigma(x^T_w\theta^w_{j-1}) & \text d_j^w=0\\ 1-\sigma(x^T_w\theta^w_{j-1}) & \text d_j^w=1 \end{cases}\tag{3.4.2} P(djw∣xw,θj−1w)={σ(xwTθj−1w)1−σ(xwTθj−1w)djw=0djw=1(3.4.2)
那么一个单词作为输出词的最大似然为:
(3.4.3) p ( w = w O ) = ∏ j = 2 L ( w ) P ( d j w ∣ x w , θ j − 1 w ) = ∏ j = 2 L ( w ) [ σ ( x w T θ j − 1 w ) ] 1 − d j w [ 1 − σ ( x w T θ j − 1 w ) ] d j w p(w=w_O)=\prod^{L(w)}_{j=2}P(d^w_j|x_w,\theta^w_{j-1}) =\prod^{L(w)}_{j=2}[\sigma(x^T_w\theta^w_{j-1})]^{1-d_j^w}[1-\sigma(x^T_w\theta^w_{j-1})]^{d_j^w}\tag{3.4.3} p(w=wO)=j=2∏L(w)P(djw∣xw,θj−1w)=j=2∏L(w)[σ(xwTθj−1w)]1−djw[1−σ(xwTθj−1w)]djw(3.4.3)
取对数:
(3.4.4) L = l o g ∏ j = 2 L ( w ) P ( d j w ∣ x w , θ j − 1 w ) = ∑ j = 2 L ( w ) ( ( 1 − d j w ) l o g [ σ ( x w T θ j − 1 w ) ] + d j w l o g [ 1 − σ ( x w T θ j − 1 w ) ] ) L=log\prod^{L(w)}_{j=2}P(d^w_j|x_w,\theta^w_{j-1}) =\sum^{L(w)}_{j=2}((1-d_j^w)log[\sigma(x^T_w\theta^w_{j-1})]+d_j^wlog[1-\sigma(x^T_w\theta^w_{j-1})])\tag{3.4.4} L=logj=2∏L(w)P(djw∣xw,θj−1w)=j=2∑L(w)((1−djw)log[σ(xwTθj−1w)]+djwlog[1−σ(xwTθj−1w)])(3.4.4)
于是可对模型参数求偏导:
(3.4.5) ∂ L ∂ θ j − 1 w = ( 1 − d j w − σ ( x w T θ j − 1 w ) ) x w \frac{\partial L}{\partial \theta^w_{j-1}}=(1-d_j^w-\sigma(x^T_w\theta^w_{j-1}))x_w\tag{3.4.5} ∂θj−1w∂L=(1−djw−σ(xwTθj−1w))xw(3.4.5)
同理
(3.4.6) ∂ L ∂ x w = ( 1 − d j w − σ ( x w T θ j − 1 w ) ) θ j − 1 w \frac{\partial L}{\partial x_w}=(1-d_j^w-\sigma(x^T_w\theta^w_{j-1}))\theta^w_{j-1}\tag{3.4.6} ∂xw∂L=(1−djw−σ(xwTθj−1w))θj−1w(3.4.6)
4.1.2 基于分层 softmax 的 CBOW 模型
假设我们取得上下文的窗口大小为 2 c 2c 2c ,即训练样本中的每一个词都以其前面和后面 c c c 个词作为输入,该词本身作为样本输出。
算法流程如下:
输入:基于 CBOW 的语料训练样本,词向量维度的大小 N N N,CBOW 的上下文大小 2 c 2c 2c,步长 η \eta η
输出:huffman 树的所有内部节点模型参数 θ \theta θ 和所有的词向量 x x x
-
第一步基于语料库构建霍夫曼树树
-
第二步随机初始化模型参数 θ \theta θ 和所有词的词向量 x x x
-
第三步计算梯度并对每个训练集中的样本 ( c o n t e x t ( w ) , w ) (context(w),w) (context(w),w)作如下处理:
-
令 e = 0 e=0 e=0,计算
KaTeX parse error: Can't use function '$' in math mode at position 50: …\tag{3.4.7} 其中 $̲x_i$ 为上下文第 $i$ …其中 x i x_i xi 为上下文第 i i i 个词的输入词向量
-
f o r j = 2 t o L ( w ) for\ j=2\ to\ L(w) for j=2 to L(w) 计算:
f = σ ( x w T ) θ j − 1 w g = ( 1 − d j w − f ) η e = e + g θ j − 1 w θ j − 1 w = θ j − 1 w + g x w f=\sigma(x^T_w)\theta^w_{j-1} \\ g=(1-d^w_j-f)\eta \\ e=e+g\theta^w_{j-1} \\ \theta^w_{j-1}=\theta^w_{j-1}+gx_w f=σ(xwT)θj−1wg=(1−djw−f)ηe=e+gθj−1wθj−1w=θj−1w+gxw -
对于 c o n t e x t ( w ) context(w) context(w) 中的每一个词向量 x i x_i xi 进行更新直到梯度收敛:
x i = x i + e x_i = x_i+e xi=xi+e
-
4.1.3 基于分层 softmax 的 Skip-Gram 模型
对于 Skip-Gram 模型来说,输入只有一个词 w w w,输出为 2 c 2c 2c 个词向量 c o n t e x t ( w ) context(w) context(w),我们期望 P ( x i ∣ x w ) , i = 1 , 2 , . . . , 2 c P(x_i|x_w),i=1,2,...,2c P(xi∣xw),i=1,2,...,2c 最大。
我们在期望 P ( x i ∣ x w ) , i = 1 , 2 , . . . 2 c P(x_i|x_w),i=1,2,...2c P(xi∣xw),i=1,2,...2c 最大时,也就是期望 P ( x w ∣ x i ) , i = 1 , 2 , . . . , 2 c P(x_w|x_i),i=1,2,...,2c P(xw∣xi),i=1,2,...,2c 最大,在训练时,word2vec 使用了后者,因为这样可以在一次迭代时不是只更新 x w x_w xw 一个词的词向量,而是 x i , i = 1 , 2 , . . . , 2 c x_i,i=1,2,...,2c xi,i=1,2,...,2c 共 2 c 2c 2c 个词的词向量,可以使得整体的迭代更加均衡。所以 Skip-Gram 模型不像 CBOW 模型对输入进行更新,而是对 2 c 2c 2c 个输出进行更新。
这里相当于把每一个原本的输出词向量作为输入,原本的输入词向量作为输出,类似上下文大小为1的 CBOW 模型,依次更新每一个输出的词向量。
算法流程如下:
输入:基于 Skip-Gram 的语料训练样本词向量维度的大小 N N N,Skip-Gram 的上下文大小 2 c 2c 2c,步长 η \eta η
输出:huffman 树的所有内部节点模型参数 θ \theta θ 和所有的词向量 x x x
-
第一步基于语料库构建霍夫曼树
-
第二步随机初始化模型参数 θ \theta θ 和所有词的词向量 x x x
-
第三步对每一个样本 ( w , c o n t e x t ( w ) ) (w,context(w)) (w,context(w)) 做如下处理:
-
$ for\ i=1\ to\ 2c$:
令 e = 0 , f o r j = 2 t o L ( w ) e=0,for\ j=2\ to\ L(w) e=0,for j=2 to L(w),计算:
f = σ ( x i T θ j − 1 w ) g = ( 1 − d j w − f ) η e = e + g θ j − 1 w θ j − 1 w = θ j − 1 w + g x i f=\sigma(x^T_i\theta^w_{j-1}) \\ g=(1-d^w_j-f)\eta \\ e=e+g\theta^w_{j-1} \\ \theta^w_{j-1}=\theta^w_{j-1}+gx_i f=σ(xiTθj−1w)g=(1−djw−f)ηe=e+gθj−1wθj−1w=θj−1w+gxi
更新每个该词的词向量:
x i = x i + e x_i=x_i+e xi=xi+e -
若梯度收敛则结束,否则回到步骤1继续迭代
-
这里与上面 CBOW 模型的区别在于,上面 CBOW 其实也是由 2 c 2c 2c 个上下文词向量来走到 Huffman 树的叶子节点,但是他的根节点为 2 c 2c 2c 个词向量的求和均值,并且更新的也是 c o n t e x t ( w ) context(w) context(w) 中的 2 c 2c 2c 个词向量。而 Skip-Gram 每次单一的输入 2 c 2c 2c 个词向量中的一个,最后更新的也是这个输入的词向量和Huffman内部节点的参数。
4.2 Negative Sampling
相比于分层 softmax ,负采样没有用到霍夫曼树,而是通过采样得到 neg 个负例加上一个真实的正例,进行二元逻辑回归,得到负采样对应每个词 w i w_i wi 对应的模型参数 θ i \theta_i θi,以及每个词的词向量。负采样每次让一个训练样本仅仅更新一小部分的权重参数,从而降低梯度下降过程中的计算量。
4.2.1 负采样的方法
若词汇表大小为 V,我们先将长度为1的线段分成 V 份,每一份对应一个词,且词频越高对应线段长度越长,词 w w w 的长度:
l e n ( w ) = c o u n t ( w ) ∑ u ∈ v o c a b c o u n t ( u ) len(w)=\frac{count(w)}{\sum_{u\in vocab}count(u)} len(w)=∑u∈vocabcount(u)count(w)
在word2vec中长度计算如下:
l e n ( w ) = c o u n t ( w ) 3 / 4 ∑ u ∈ v o c a b c o u n t ( u ) 3 / 4 len(w)=\frac{count(w)^{3/4}}{\sum_{u\in vocab}count(u)^{3/4}} len(w)=∑u∈vocabcount(u)3/4count(w)3/4
采样前,我们将线段均匀划分成 M(默认为 1 0 8 10^8 108)份,且 M >> V,这样每个划分点 m i , i = 0 , 1 , 2 , . . . , M m_i,i=0,1,2,...,M mi,i=0,1,2,...,M 都对会落在某一个词的线段上,我们只需要从这 M+1 个点上采样出 neg 个位置就行,其对应的词就是我们需要的负例,且注意不要采到正例。
4.2.2 模型参数的梯度计算
假设通过负采样,我们得到 n e g neg neg 个负例 ( c o n t e x t ( w ) , w i ) , i = 1 , 2 , . . . , n e g (context(w),w_i),i=1,2,...,neg (context(w),wi),i=1,2,...,neg,并假设正例词为 w 0 w_0 w0
那么我们正例和负例期望满足:
P ( c o n t e x t ( w 0 ) , w i ) = σ ( x w 0 T θ w i ) , y i = 1 , i = 0 P ( c o n t e x t ( w 0 ) , w i ) = 1 − σ ( x w 0 T θ w i ) , y i = 0 , i = 1 , 2 , . . . , n e g P(context(w_0),w_i)=\sigma(x^T_{w_0}\theta^{w_i}),\quad y_i=1,i=0 \\ P(context(w_0),w_i)=1-\sigma(x^T_{w_0}\theta^{w_i}),\quad y_i=0,i=1,2,...,neg P(context(w0),wi)=σ(xw0Tθwi),yi=1,i=0P(context(w0),wi)=1−σ(xw0Tθwi),yi=0,i=1,2,...,neg
最大似然为:
P ( w = w 0 ) = ∏ i = 0 n e g P ( c o n t e x t ( w 0 ) , w i ) = ∏ i = 0 n e g [ σ ( x w 0 T θ w i ) ] y i [ 1 − σ ( x w 0 T θ w i ) ] 1 − y i P(w=w_0)=\prod^{neg}_{i=0}P(context(w_0),w_i) =\prod^{neg}_{i=0}[\sigma(x^T_{w_0}\theta^{w_i})]^{y_i}[1-\sigma(x^T_{w_0}\theta^{w_i})]^{1-y_i} P(w=w0)=i=0∏negP(context(w0),wi)=i=0∏neg[σ(xw0Tθwi)]yi[1−σ(xw0Tθwi)]1−yi
取对数
L = ∑ i = 0 n e g y i l o g ( σ ( x w 0 T θ w i ) ) + ( 1 − y i ) l o g ( 1 − σ ( x w 0 T θ w i ) ) L=\sum^{neg}_{i=0}y_ilog(\sigma(x^T_{w_0}\theta^{w_i}))+(1-y_i)log(1-\sigma(x^T_{w_0}\theta^{w_i})) L=i=0∑negyilog(σ(xw0Tθwi))+(1−yi)log(1−σ(xw0Tθwi))
首先计算 θ w i \theta^{w_i} θwi 的梯度:
∂ L ∂ θ w i = y i ( 1 − σ ( x w 0 T θ w i ) ) x w 0 − ( 1 − y i ) σ ( x w 0 T θ w i ) x w 0 = ( y i − σ ( x w 0 T θ w i ) ) x w 0 \frac{\partial L}{\partial \theta^{w_i}}=y_i(1-\sigma(x^T_{w_0}\theta^{w_i}))x_{w_0}-(1-y_i)\sigma(x^T_{w_0}\theta^{w_i})x_{w_0} =(y_i-\sigma(x^T_{w_0}\theta^{w_i}))x_{w_0} ∂θwi∂L=yi(1−σ(xw0Tθwi))xw0−(1−yi)σ(xw0Tθwi)xw0=(yi−σ(xw0Tθwi))xw0
同理可得 x w 0 x_{w_0} xw0 的梯度:
∂ L ∂ θ w 0 = ∑ i = 0 n e g ( y i − σ ( x w 0 T θ w i ) ) θ w 0 \frac{\partial L}{\partial \theta^{w_0}}= \sum^{neg}_{i=0}(y_i-\sigma(x^T_{w_0}\theta^{w_i}))\theta^{w_0} ∂θw0∂L=i=0∑neg(yi−σ(xw0Tθwi))θw0
4.2.3 基于负采样的 CBOW 模型
假设我们取得上下文的窗口大小为 2 c 2c 2c ,即训练样本中的每一个词都以其前面和后面 c c c 个词作为输入,该词本身作为样本输出。
算法流程如下:
输入:语料训练样本,词向量维度的大小 N N N,CBOW 的上下文窗口大小 2 c 2c 2c,步长 η \eta η,以及负采样的个数 $neg $
输出:词汇表每个词对应的模型参数 θ \theta θ 和所有的词向量 x x x
-
第一步随机初始化所有的模型参数 θ w \theta^w θw,所有的词向量 x w x_w xw
-
第二步对每个训练样本 c o n t e x t ( w 0 ) , w 0 ) context(w_0),w_0) context(w0),w0),进行负采样,得到 n e g neg neg 个负例词 $w_i,i=1, 2,…,neg $
-
第三步进行梯度上升迭代过程,对训练语料中的每一个样本 ( c o n t e x t ( w 0 ) , w 0 , w 1 , . . . , w n e g ) (context(w_0),w_0,w_1,...,w_{neg}) (context(w0),w0,w1,...,wneg)做如下处理:
-
令 e = 0 e=0 e=0,计算隐含层输出:
x w 0 = 1 2 c ∑ i = 1 2 c x i x_{w_0}=\frac 1{2c}\sum ^{2c}_{i=1}x_i xw0=2c1i=1∑2cxi -
f o r i = 0 t o n e g for\ i=0\ to\ neg for i=0 to neg,计算:
f = σ ( x w 0 T θ w i ) g = ( y i − f ) η e = e + g θ w i θ w i = θ w i + g x w 0 f=\sigma(x^T_{w_0}\theta^{w_i}) \\ g=(y_i-f)\eta \\ e = e+g\theta^{w_i} \\ \theta^{w_i}=\theta^{w_i}+gx_{w_0} f=σ(xw0Tθwi)g=(yi−f)ηe=e+gθwiθwi=θwi+gxw0 -
根据梯度对 c o n t e x t ( w ) context(w) context(w) 中的每一个词向量 x k x_k xk(2c 个)进行更新:
x k = x k + e x_k = x_k+e xk=xk+e -
若梯度收敛,结束迭代,否则回到第三步进行迭代更新
-
4.2.4 基于负采样的 Skip-Gram 模型
与基于层级 softmax 的 Skip-Gram 模型一样,这里也是对 2 c 2c 2c 个输出词向量进行迭代更新。
算法流程如下:
输入:基于 Skip-Gram 的语料训练样本,词向量的维度大小 N,Skip-Gram 的上下文大小 2 c 2c 2c,步长 η \eta η,负采样的个数 n e g neg neg 。
输出:词汇表每个词对应的模型参数 θ w \theta^w θw,所有词向量 x w x_w xw
-
第一步随机初始化所有的模型参数 θ \theta θ 和词向量 x x x
-
第二步对每个训练样本 ( c o n t e x t ( w 0 ) , w 0 ) (context(w_0),w_0) (context(w0),w0) 采样出 n e g neg neg 个负例词 w i , i = 1 , 2 , . . . , n e g w_i,i=1,2,...,neg wi,i=1,2,...,neg
-
第三步进行梯度上升,并更新参数,对每个样本 ( c o n t e x t ( w 0 ) , w 0 , w 1 , . . . , w n e g ) (context(w_0),w_0,w_1,...,w_{neg}) (context(w0),w0,w1,...,wneg) 做如下处理:
-
f o r i = 1 t o 2 c : for\ i=1\ to\ 2c: for i=1 to 2c:
令 e = 0 , f o r j = 0 t o n e g e=0,for\ j=0\ to\ neg e=0,for j=0 to neg,计算:
f = σ ( x w 0 T θ w j ) g = ( y j − f ) η e = e + g θ w j θ w j = θ w j + g x w 0 i f=\sigma(x^T_{w_0}\theta^{w_j}) \\ g=(y_j-f)\eta \\ e=e+g\theta^{w_j} \\ \theta^{w_j}=\theta^{w_j}+gx_{w_{0i}} \\ f=σ(xw0Tθwj)g=(yj−f)ηe=e+gθwjθwj=θwj+gxw0i
利用梯度对该输出词向量进行更新:
x w 0 i = x w 0 i + e x_{w_0}^i=x_{w_0}^i+e xw0i=xw0i+e
其中 x w 0 i x^i_{w_0} xw0i 为中心词为 w 0 w_0 w0 的上下文 2 c 2c 2c 个词中的第 i i i 个词的词向量 -
若梯度收敛,结束迭代,否则回到1继续迭代更新参数
-
四、GloVe
1. 简单介绍
GloVe 全称叫 Global Vectors for Word Representation,是一个基于全局词频统计(count-based&overall statistics)的词表征(word representation)工具,与 word2vec 一样,她也是将每一个词表示成一个向量。
GloVe 结合了 LSA 和 word2vec 两者的优点,充分利用了所有语料全局信息,更易于优化且训练速度更快,但仅仅只关注了词语的共现关系,忽略了词语的顺序关系,因此训练出来的词向量包含的语义信息有限,只能进行一些词语相似度等有限的任务。
2. 基本原理
GloVe 的实现可分为三步:
-
根据语料库构建一个共现矩阵(Co-ocurrence Matrix) X X X
-
构建词向量和共现矩阵之间的近似关系,论文作者提出的关系式为:
(4.1) w i T w ‾ j + b i + b ‾ j = l o g ( X i j ) w^T_i\overline w_j+b_i+\overline b_j=log(X_{ij})\tag{4.1} wiTwj+bi+bj=log(Xij)(4.1)
其中 w i T w_i^T wiT 和 w ‾ j \overline w_j wj 是我们最终要求解的词向量, b i b_i bi 和 b ‾ j \overline b_j bj 分别是两个词向量的偏置 -
构造损失函数:
(4.2) L o s s = ∑ i , j = 1 V f ( X i j ) ( w i T w ‾ j + b i + b ‾ j − l o g ( X i j ) ) 2 Loss=\sum^V_{i,j=1}f(X_{ij})(w^T_i\overline w_j+b_i+\overline b_j-log(X_{ij}))^2\tag{4.2} Loss=i,j=1∑Vf(Xij)(wiTwj+bi+bj−log(Xij))2(4.2)
这实际上是一个加了一个权重函数 f ( X i j ) f(X_{ij}) f(Xij) 的均方误差,而且我们希望:- 一起出现次数多的单词的权重要大于那些很少一起出现的单词,所以 f f f 是非递减函数
- 而且这个权重不能过大,到一定程度后不再增加
- 如果两个单词没有一起出现过,即 X i j = 0 X_{ij}=0 Xij=0,那么它们不应该参与到 Loss 的计算中去,所以 f f f 要满足 f ( 0 ) = 0 f(0)=0 f(0)=0
作者使用的是如下函数:
(4.3) f ( x ) = { ( x / x m a x ) α i f x < x m a x 1 o t h e r w i s f(x)=\begin{cases} (x/x_{max})^\alpha & if\ x<x_{max} \\ 1 & otherwis \end{cases} \tag{4.3} f(x)={(x/xmax)α1if x<xmaxotherwis(4.3)
其中 α = 0.75 , x m a x = 100 \alpha=0.75,x_{max}=100 α=0.75,xmax=100 -
根据 Loss 计算梯度并更新参数
2.1 共现矩阵
共现矩阵中的每一个元素 X i j X_{ij} Xij 代表的是以单词 i i i 为中心词时,单词 j j j 在特定大小的上下文窗口内共同出现的次数。一般来说次数最小单位是1,但是 GloVe 根据两个单词在上下文窗口的距离 d d d,增加了一个衰减函数 d e c a y = 1 / d decay=1/d decay=1/d,也就是距离越远的两个单词所占总计数的权重越小
3. 公式推导
-
我们先定义一些变量:
- X i j X_{ij} Xij 表示单词 j j j 出现在单词 i i i 的上下文中的次数
- X i = ∑ k X i k X_i=\sum^kX_{ik} Xi=∑kXik 表示单词 i i i 的上下文中所有单词出现的总次数
- P i j = P ( j ∣ i ) = X i j / X i P_{ij}=P(j|i)=X_{ij}/X_i Pij=P(j∣i)=Xij/Xi 表示单词 j j j 出现在单词 i i i 的上下文中的概率
-
核心思想是,对任意的词 i i i 和词 j j j,以及第三个词 k k k,如果词 k k k 与词 i i i 比词 k k k 与词 j j j 有更深的关联,我们就有:
(4.4) P i k > P j k P_{ik}>P_{jk}\tag{4.4} Pik>Pjk(4.4)
且它们的比值很大,同理若词 j j j 比词 k k k 与词 i i i 有更深的关联,那么它们的比值越小,若它们都很相关或者都不相关,则比值接近于1 。 -
由上可以构造出如下函数:
(4.5) F ( w i , w j , w ‾ k ) = P i k P j k F(w_i,w_j,\overline w_k)=\frac{P_{ik}}{P_{jk}} \tag{4.5} F(wi,wj,wk)=PjkPik(4.5)
其中 w i w_i wi 和 w j w_j wj 是我们要比较的两个词向量, w ‾ k \overline w_k wk 是其他的词向量,函数 F F F 的参数和具体形式未定 -
又因为向量空间是线性的,我们可以用作差的方式衡量两个向量的差异,于是 ( 3.2 ) (3.2) (3.2)式可以变换成如下形式:
(4.6) F ( ( w i − w j ) , w ‾ k ) = P i k P j k F((w_i-w_j),\overline w_k)=\frac{P_{ik}}{P_{jk}} \tag{4.6} F((wi−wj),wk)=PjkPik(4.6) -
对上式可以发现右侧是个数量,左侧参数都是向量,于是可以对左侧两个向量做一个内积:
(4.7) F ( ( w i − w j ) T w ‾ k ) = P i k P j k F((w_i-w_j)^T\overline w_k)=\frac{P_{ik}}{P_{jk}} \tag{4.7} F((wi−wj)Twk)=PjkPik(4.7) -
回到问题本身,我们要是基于 cooccur 进行计算的,实际上在一次共现中词 w i , w j w_i,w_j wi,wj 是同等地位的,我们需要 F ( w i , w j ) = = F ( w j , w i ) F(w_i,w_j)==F(w_j,w_i) F(wi,wj)==F(wj,wi),而现在的公式是不满足的,故而我们需要给 F F F 一个约束(套一层指数运算),将差的形式变成商的形式,使得 F F F 是一个同态变换:
(4.8) F ( ( w i − w j ) T w ‾ k ) = F ( w i T w ‾ k ) F ( w j T w ‾ k ) F((w_i-w_j)^T\overline w_k)=\frac{F(w^T_i\overline w_k)}{F(w^T_j\overline w_k)} \tag{4.8} F((wi−wj)Twk)=F(wjTwk)F(wiTwk)(4.8) -
这样,由 ( 3.4 ) (3.4) (3.4)和 ( 3.5 ) (3.5) (3.5)式,可得:
(4.9) F ( w i T ) = P i k = X i k X i F(w_i^T)=P_{ik}=\frac{X_{ik}}{X_i} \tag{4.9} F(wiT)=Pik=XiXik(4.9) -
然后我们令 F = e x p F=exp F=exp,两边取对数于是有:
(4.10) w i T w ‾ k = l o g ( P i k ) = l o g ( X i k ) − l o g ( X i ) w^T_i\overline w_k=log(P_{ik})=log(X_{ik})-log(X_i) \tag{4.10} wiTwk=log(Pik)=log(Xik)−log(Xi)(4.10) -
但是公式还是没有满足对称性(当交换词 w i w_i wi 和词 w ‾ k \overline w_k wk 时公式不一致),且 l o g ( X i ) log(X_i) log(Xi) 只与 i i i 有关,我们将其吸纳进 w i w_i wi 的偏置 b i b_i bi,同时我们可以针对 w ‾ k \overline w_k wk 加一个偏置 b k b_k bk :
(4.11) w i T w ‾ k + b i + b k = l o g ( X i k ) w^T_i\overline w_k+b_i+b_k=log(X_{ik})\tag{4.11} wiTwk+bi+bk=log(Xik)(4.11)
五、ELMo
1. 简单介绍
ELMo 是一种新型的语境化的词嵌入(contextualized word-embeddings)模型,可对词进行复杂特征(如句法和语义)和词在语言语境中的变化进行建模(即对多义词进行建模),根据单词在句子的上下文中表示的不同含义,给它们不同的表征。打破了之前 word2vec 一个词对应一个词向量的 embedding 方式。
ELMo的主要做法是先训练一个完整的语言模型,再用这个语言模型去处理需要训练的文本,生成相应的词向量,它使用针对特定任务的双向 LSTM 来创建嵌入。同时它用到了 finetuning 的技巧,在预训练好的模型上,我们只需让其在我们自己的训练数据上进行微调就能使用。
2. 基本原理
ELMo 最重要的就是训练的语言模型,模型结构如下:
它使用的是一个双向的 LSTM 语言模型,目标函数就是取这两个方向的语言模型的最大似然。
前向 LSTM:
p ( t 1 , t 2 , . . . , t N ) = ∏ k = 1 N p ( t k ∣ t 1 , t 2 , . . . , t k − 1 ) p(t_1,t_2,...,t_N)=\prod^N_{k=1}p(t_k|t_1,t_2,...,t_{k-1}) p(t1,t2,...,tN)=k=1∏Np(tk∣t1,t2,...,tk−1)
反向 LSTM:
p ( t 1 , t 2 , . . . , t N ) = ∏ k = 1 N p ( t k ∣ t k + 1 , t k + 2 , . . . , t N ) p(t_1,t_2,...,t_N)=\prod^N_{k=1}p(t_k|t_{k+1},t_{k+2},...,t_N) p(t1,t2,...,tN)=k=1∏Np(tk∣tk+1,tk+2,...,tN)
最大似然函数:
∑ k = 1 N ( l o g p ( t k ∣ t 1 , t 2 , . . . , t k − 1 ) + l o g p ( t k ∣ t k + 1 , t k + 2 , . . . , t N ) ) \sum^N_{k=1}(logp(t_k|t_1,t_2,...,t_{k-1})+logp(t_k|t_{k+1},t_{k+2},...,t_N)) k=1∑N(logp(tk∣t1,t2,...,tk−1)+logp(tk∣tk+1,tk+2,...,tN))
其中 ( t 1 , t 2 , . . . , t N ) (t_1,t_2,...,t_N) (t1,t2,...,tN) 是一系列的 tokens,对每一个 tokens,一个 L 层的双向 LSTM 要计算出 L+1 个表征(词向量),我们可以取最后的一个表征作为我们需要的词向量,也可以综合所有的表征做加权求和得到最终结果。
2.1 具体步骤
对于一个 supervise NLP 任务,可以分为三步:
- 产生预训练好的双向语言模型,模型由两层的双向 LSTM 组成,之间可由残差连接
- 在任务语料上 finetuning(无监督训练)进一步得到语言模型
- 利用 ELMo 的 word embedding 进行上层任务的训练
3. 模型评价
3.1 优点
-
ELMo 训练词向量是基于上下文变化而改变的,所以在一词多意方面 ELMo 的效果一定比 word2vec 要好。
-
ELMo 利用了双向的 LSTM 模型,能看到更长的上下文信息,更加准确代表一个词的意思。
-
ELMo 还有一个优势,就是它建立语言模型的时候,可以运用非任务的超大语料库去学习,一旦学习好了,可以平行的运用到相似问题上。
3.2 缺点
- ELMo 对双向 LSTM 模型的输出只是采取的简单的拼接,并不能很好地融合双向的语义信息。
- 双向 LSTM 模型对语义的提取不如 Transformer。
六、GPT
1. 简单介绍
GPT 是一种半监督的处理语言理解任务的模型,使用非监督的预训练和监督方式的微调。模型的目标是学习一个通用的表示,经过很小的调整就能在大量任务上进行应用,而且这个模型不需要目标任务和非标注的数据集在同一个领域,模型分为两个阶段:
- 用语言模型预训练好一个深度模型
- 使用相应的有标签的数据将这个模型的参数调整到目标任务
2. 模型结构和基本原理
2.1 无监督预训练
预训练过程是对非监督文本 ( x 1 , x 2 , . . . , x m ) (x_1,x_2,...,x_m) (x1,x2,...,xm) 的处理,我们的目标是用语言模型去最大化语言模型的极大似然:
(6.1) L 1 ( X ) = ∑ i l o g P ( x i ∣ x i − k , . . . , x i − 1 ; Θ ) L_1(X)=\sum_ilogP(x_i|x_{i-k},...,x_{i-1};\Theta)\tag{6.1} L1(X)=i∑logP(xi∣xi−k,...,xi−1;Θ)(6.1)
其中 k k k 是文本窗口的大小(即预测需要的上文的长度)
GPT 用的是多层 Transformer 的 Decoder 模型,这个模型应用了多头自注意力机制。模型的输入是词向量加位置向量:
(6.2) h 0 = U W e + W p h_0=UW_e+W_p\tag{6.2} h0=UWe+Wp(6.2)
其中 U = ( u k , . . . , u 1 ) U=(u_k,...,u_1) U=(uk,...,u1) 是 tokens 的文本向量(One-hot), W e W_e We 是词嵌入矩阵, W p W_p Wp 是嵌入矩阵的位置编码。
再经过12层的 Transformer 模块:
(6.3) h l = t r a n s f o r m e r _ b l o c k ( h l − 1 ) f o r ∀ i ∈ [ 1 , n ] h_l=transformer\_block(h_{l-1})\ for\ \forall i\in [1,n]\tag{6.3} hl=transformer_block(hl−1) for ∀i∈[1,n](6.3)
其中 n n n 是网络的层数, h l h_l hl 是隐藏层第 l l l 层的输出。
最后通过一个全连接加 softmax 预测第 k 个词:
(6.4) P ( u ) = s o f t m a x ( h n W e T ) P(u)=softmax(h_nW_e^T)\tag{6.4} P(u)=softmax(hnWeT)(6.4)
2.2 有监督微调
在使用 ( 6.1 ) (6.1) (6.1)中的目标对模型进行预训练后,我们再利用有监督目标任务对这些模型参数进行微调。假设一个带标签的数据集 C → ( x 1 , x 2 , . . . , x m , y ) ∈ C C\rightarrow(x^1,x^2,...,x^m,y)\in C C→(x1,x2,...,xm,y)∈C,输入 ( x 1 , x 2 , . . . , x m ) (x^1,x^2,...,x^m) (x1,x2,...,xm) 经过我们预训练的模型得到最后的输出向量 h l m h^m_l hlm,然后通过一个附加的线性层和 softmax 预测标签:
(6.5) P ( y ∣ x 1 , x 2 , . . . , x m ) = s o f t m a x ( h l m W y ) P(y|x^1,x^2,...,x^m)=softmax(h^m_lW_y)\tag{6.5} P(y∣x1,x2,...,xm)=softmax(hlmWy)(6.5)
最大似然函数:
(6.6) L 2 = ∑ x , y l o g P ( y ∣ x 1 , x 2 . . . , x m ) L_2=\sum_{x,y}logP(y|x^1,x^2...,x^m)\tag{6.6} L2=x,y∑logP(y∣x1,x2...,xm)(6.6)
另外,我们增加了语言模型辅助微调,提高了模型的泛化和收敛速度,最后的损失函数为:
(6.7) L 3 ( C ) = L 2 ( C ) + λ ∗ L 1 ( C ) L_3(C)=L_2(C)+\lambda *L_1(C)\tag{6.7} L3(C)=L2(C)+λ∗L1(C)(6.7)
2.3 下游任务的改造:
对于分类问题,不用怎么动,加上一个起始和终结符号即可;对于句子关系判断问题,比如Entailment,两个句子中间再加个分隔符即可;对文本相似性判断问题,把两个句子顺序颠倒下做出两个输入即可,这是为了告诉模型句子顺序不重要;对于多项选择问题,则多路输入,每一路把文章和答案选项拼接作为输入即可。
3. 模型评价
3.1 优点
- GPT 用的 Transformer 作为特征抽取器,其效果要比 LSTM 好
- 计算速度更快,易于并行化
3.2 缺点
- 对不同类型的任务需要对输入数据做不同的调整
- 在进行预训练时只用了上文的信息预测而抛开了下文
七、Bert
1. 简单介绍
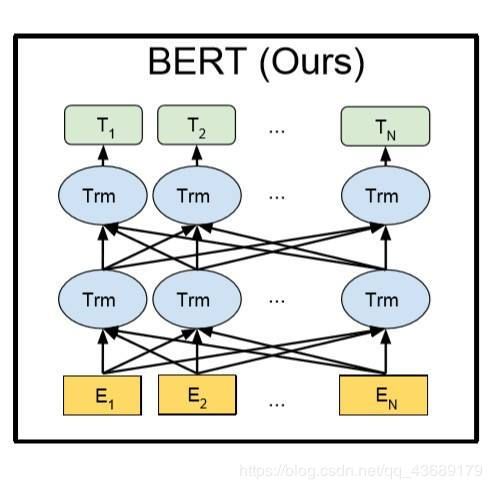
BERT 的全称是Bidirectional Encoder Representation from Transformers,即双向Transformer的Encoder。BERT 采用和 GPT 完全相同的两阶段模型,即语言模型预训练加 fine-tuning 解决下游任务,不同的是 BERT 在预训练过程采用了类似 ELMo 的双向语言模型。
BERT 模型结构如下:
2. 基本原理
2.1 Masked Language Model
顾名思义,masked 语言模型就是指在预训练时对所有语料随机 mask 掉其中15%的 token,然后模型会尝试基于序列中其他未被 mask 的上下文来预测被掩盖的原单词。
因为对于 maske 的这个标记在下游 NLP 任务中并不存在,为了和后续任务保持一致,作者又在15%的基础上:
- 有80%的概率用“[mask]”标记替换该词
- 有10%的概率用随机采样的一个单词替换改词
- 有10%的概率不做替换
2.2 Next Sentence Representation(NSP)
在很多任务中,只是依靠词嵌入是不足以完成任务的(只学到了一堆 token 级的特征),我们还需要捕捉一些句子级别的特征来完成 SLI、QA、dialogue 等需要句子表示、句间交互与匹配的任务,于是BERT 又引入了另一个极其重要却又极其轻量级的任务 NSP,来试图把这种模式也学习到。
-
句子级负采样:
在预训练过程中,模型接受成对的句子作为输入,并预测第二句话是否是第一句话的后续句子,其中有50%的输入是前后关系,50%的输入是从语料库中随机采样组成的非前后关系的句子。
-
句子级表示:
BERT 把两句话会整合成一句话进行输入,为了帮助模型区分开训练中的两个句子,BERT 在每个输入前面加一个 [CLS] 标记,在每一句话后面加一个 [SEP] 标记,因为 Transformer 是可以无视空间和距离的把全局信息 encoding 进每一个位置的,故而我们可以用 [CLS] 的最高隐藏层输出作为句子/句子对的表征,预测句子对是否是上下文也可以用一个简单的分类层将 [CLS] 标记的输出变换为 2 维的向量并 通过 softmax 计算概率进行训练。
-
segment embedding:
另外,相对于 GPT,BERT 对输入的词嵌入不仅加了位置的编码信息,还加入了segment embedding。如下图所示,对于句子对来说, E A E_A EA 和 E B E_B EB 分别代表左句子和右句子,对于句子来说,只有 E A E_A EA,最终输入结果是由 Token Embedding、Segment Embedding 和 Position Embedding 三者拼接而成
2.3 下游任务的改造
-
对于句子关系类任务,和GPT类似,加上一个起始和终结符号,句子之间加个分隔符即可。对于输出来说,把第一个起始符号对应的Transformer最后一层位置上面串接一个softmax分类层即可。
-
对于分类问题,与GPT一样,只需要增加起始和终结符号,输出部分和句子关系判断任务类似改造。
-
对于序列标注问题,输入部分和单句分类是一样的,只需要输出部分Transformer最后一层每个单词对应位置都进行分类即可。
-
对于机器翻译或者文本摘要,聊天机器人这种生成式任务,同样可以稍作改造即可引入Bert的预训练成果。只需要附着在S2S结构上,encoder部分是个深度Transformer结构,decoder部分也是个深度Transformer结构。根据任务选择不同的预训练数据初始化encoder和decoder即可。这是相当直观的一种改造方法。当然,也可以更简单一点,比如直接在单个Transformer结构上加装隐层产生输出也是可以的。
3. 模型评价
3.1 优点
- 采用的是 Transformer 双向语言模型,捕捉到的是真正意义上的 bidirectional context 信息。
- 在训练 BERT 模型时,Masked LM 和 Next Sentence Prediction 是一起训练的,目标就是要最小化两种策略的组合损失函数,前者用于建模更广发的上下文,后者用来建模多个句子间的关系。
- 另外预训练数据量的
3.2 缺点
- 每个 batch 只有15%的 token 被预测,所以 BERT 收敛得比 left-to-right 模型要慢。
- [mask] 标记在实际预测中不会出现,训练时用过多 [mask] 影响模型表现,且在下游任务中 fine-tuning 没有 [mask] 标记,导致上下游任务训练不一致。
八、GPT 2.0
1. 训练数据集
为了获取多样、体量庞大且又有质量的数据作为训练样本最终只用人工筛选过的网页内容,但是人工过滤爬虫内容是很贵的,因此我们只是把这个作为一个起点,我们爬取了Reddit上所有的外部链接,每个链接的karma值至少要有3分,最终得到800多万个文档,总共40G的数据作为训练样本
2. 输入表示
作者没有采用 word-level 或者 character-level 的嵌入,而是采用了 Byte Pair Encoding (BPE), 这种输入表示允许我们将字级语言模型的经验优势与字节级方法的通用性结合起来。因为我们的方法能给任何一个unicode字符串分配一个概率,所以该语言模型对任何数据集都不用做预处理。
BPE是一种介于字符级和字级之间的实用语言模型,它能有效地在频繁符号序列的字级输入和不频繁符号序列的字符级输入之间进行插值,尽管名为BPE,但实际是在处理Unicode编码,而不是字节序列,该方法需要包含所有unicode编码,以便能对所有Unicode字符串建模,在添加任何多符号标记之前,该方法的基本词汇表超过13万。与BPE经常使用的3.2万到6.4万个词汇相比,这个数字大得令人望而却步。相比之下,字节级别的BPE需要的词典大小只有256,
然而,直接将BPE应用于字节序列会导致合并无法达到最优解,因为BPE使用贪婪算法来构建词汇表。我们发现BPE包含了许多像dog这样的常用的词,因为它们出现在许多变体中,比如dog,dog?dog。诸如此类的。该结果将会导致词典词槽分配与模型能力受到限制。为了避免这个问题,我们会防止BPE跨字符类别合并任何字节序列,我们为空格添加了一个异常,它显著地提高了压缩效率,同时只在多个vocab标记之间添加了最小的单词碎片。
3. 模型的改进
相对于 GPT,GPT 2.0 做了少量的修改:
- 将layer normalization移到每个sub-block入口
- 在最后的self-attention模块中添加了layer normalization
- 修改初始化残差层权重的权值乘以 1 / N 1/\sqrt{N} 1/N,其中 N 是残差层的数量
- 词典被扩展到了50257,context 的维度从 512 提高到了 1024 并且 batchsize 采用了512
参考资料
https://www.jianshu.com/p/9fe0a7004560
https://blog.csdn.net/roger__wong/article/details/41175967
https://zhuanlan.zhihu.com/p/53425736
https://blog.csdn.net/u010995990/article/details/79805321
https://www.cnblogs.com/pinard/p/7249903.html
https://blog.csdn.net/u010089444/article/details/52624964?ref=myread
https://www.jianshu.com/p/5bbb55c35961
https://blog.csdn.net/triplemeng/article/details/82380202
https://www.cnblogs.com/huangyc/p/9860430.html
常,它显著地提高了压缩效率,同时只在多个vocab标记之间添加了最小的单词碎片。
3. 模型的改进
[外链图片转存中…(img-995uI4ZS-1564969549894)]
相对于 GPT,GPT 2.0 做了少量的修改:
- 将layer normalization移到每个sub-block入口
- 在最后的self-attention模块中添加了layer normalization
- 修改初始化残差层权重的权值乘以 1 / N 1/\sqrt{N} 1/N,其中 N 是残差层的数量
- 词典被扩展到了50257,context 的维度从 512 提高到了 1024 并且 batchsize 采用了512
参考资料
https://www.jianshu.com/p/9fe0a7004560
https://blog.csdn.net/roger__wong/article/details/41175967
https://zhuanlan.zhihu.com/p/53425736
https://blog.csdn.net/u010995990/article/details/79805321
https://www.cnblogs.com/pinard/p/7249903.html
https://blog.csdn.net/u010089444/article/details/52624964?ref=myread
https://www.jianshu.com/p/5bbb55c35961
https://blog.csdn.net/triplemeng/article/details/82380202
https://www.cnblogs.com/huangyc/p/9860430.html
[Mikolov T, Chen K, Corrado G, et al. Efficient Estimation of Word Representations in Vector SpaceJ]. Computer Science, 2013.