一文带你彻底搞懂二叉树(Python实现)——真香

前言

终于到了数据结构中的关键部分了——二叉树。说起二叉树啊，简直是我当初学习C语言数据结构课程的噩梦，为什么这么说呢？记得老师当初在讲啥子先序遍历、中序遍历、后序遍历的时候，我脑壳里简直是一团浆糊，碰到一些复杂的二叉树根本就整不清楚到底要咋个遍历，并且遍历的代码到现在我还不会。害，以至于我在期末考试之前猛补数据结构的知识点，本以为自己能够得个高分（题目都会做），结果差强人意。现在我重新捡起这个，用一种全新的思维方式来解释二叉树、实现二叉树，猛地发现Python实现是真香。

树

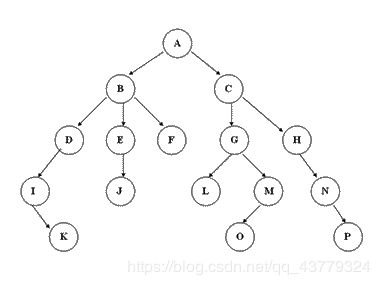
这里的树不是树，是一种二维层次的数据结构类型，只是长的像树，准确来说是长的像一个倒着的树，不过我觉得说是长的像树根最为贴切。
树（英语：tree）是一种抽象数据类型（ADT）或是实作这种抽象数据类型的数据结构，用来模拟具有树状结构性质的数据集合。它是由n（n>=1）个有限节点组成一个具有层次关系的集合。树具有如下特点：

• 每个节点有零个或多个子节点；
• 没有父节点的节点称为根节点；
• 每一个非根节点有且只有一个父节点；
• 除了根节点外，每个子节点可以分为多个不相交的子树；

以上就是一些树的大致结构图。

树中的一些术语

• 节点的度：一个节点含有的子树的个数称为该节点的度；
• 树的度：一棵树中，最大的节点的度称为树的度；
• 叶节点或终端节点：度为零的节点；
• 父亲节点或父节点：若一个节点含有子节点，则这个节点称为其子节点的父节点；
• 孩子节点或子节点：一个节点含有的子树的根节点称为该节点的子节点；
• 兄弟节点：具有相同父节点的节点互称为兄弟节点；
• 节点的层次：从根开始定义起，根为第1层，根的子节点为第2层，以此类推；
• 树的高度或深度：树中节点的最大层次；
• 堂兄弟节点：父节点在同一层的节点互为堂兄弟；
• 节点的祖先：从根到该节点所经分支上的所有节点；
• 子孙：以某节点为根的子树中任一节点都称为该节点的子孙。
• 森林：由m（m>=0）棵互不相交的树的集合称为森林；

这些我们大致了解一下就可以了，知道有这么个东西，然后会求解一些问题，如果不是做题的话，没必要了解的特别的清楚。

树的分类

• 无序树：树中任意节点的子节点之间没有顺序关系，这种树称为无序树，也称为自由树；
• 有序树：树中任意节点的子节点之间有顺序关系，这种树称为有序树；
• 二叉树：每个节点最多含有两个子树的树称为二叉树；
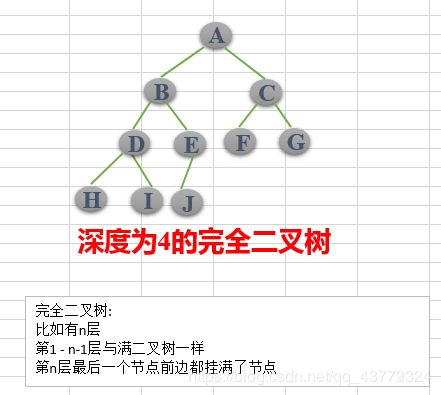
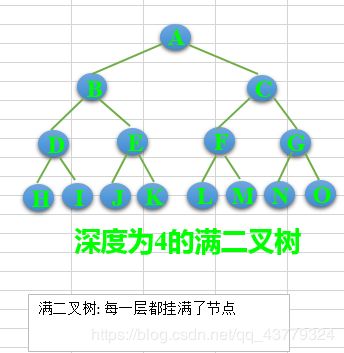
  • 完全二叉树：对于一颗二叉树，假设其深度为d(d>1)。除了第d层外，其它各层的节点数目均已 达最大值，且第d层所有节点从左向右连续地紧密排列，这样的二叉树被称为完全二叉树，其中满二叉树的定义是所有叶节点都在最底层的完全二叉树;
  • 平衡二叉树（AVL树）：当且仅当任何节点的两棵子树的高度差不大于1的二叉树；
  • 排序二叉树（二叉查找树（英语：Binary Search Tree），也称二叉搜索树、有序二叉树）；
• 霍夫曼树（用于信息编码）：带权路径最短的二叉树称为哈夫曼树或最优二叉树；
• B树：一种对读写操作进行优化的自平衡的二叉查找树，能够保持数据有序，拥有多余两个子树。

树的存储表示

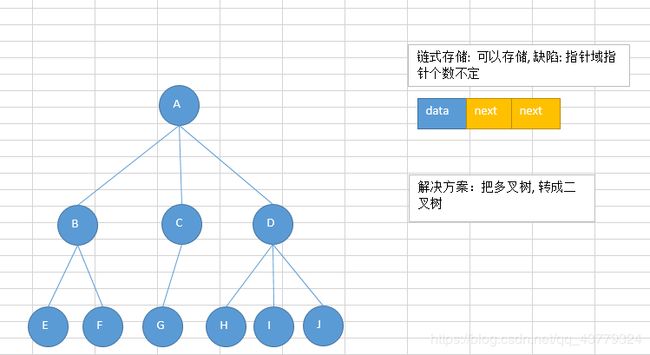
树的存储一般是顺序存储或者链式存储，即采用顺序表或者链表。
顺序存储：将数据结构存储在固定的数组中，在遍历速度上有一定的优势，但因所占空间比较大，是非主流二叉树。二叉树通常以链式存储。

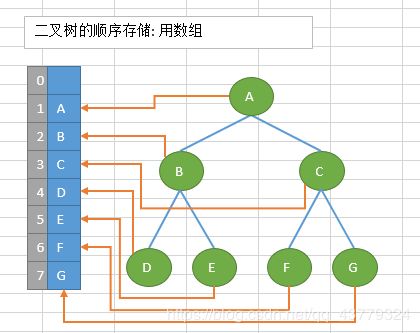
链式存储：采用链表的方式来存储二叉树的各个结点。

二叉树

二叉树是每个节点最多有两个子树的树结构。通常子树被称作“左子树”（left subtree）和“右子树”（right subtree）。

二叉树的性质

• 性质1: 在二叉树的第i层上至多有2^(i-1)个结点（i>0）
• 性质2: 深度为k的二叉树至多有2^k - 1个结点（k>0）
• 性质3: 对于任意一棵二叉树，如果其叶结点数为N0，而度数为2的结点总数为N2，则N0=N2+1;
• 性质4:具有n个结点的完全二叉树的深度必为 log2(n+1)
• 性质5:对完全二叉树，若从上至下、从左至右编号，则编号为i 的结点，其左孩子编号必为2i，其右孩子编号必为2i＋1；其双亲的编号必为i/2（i＝1 时为根,除外）

二叉树的实现

前面吧啦吧啦半天感觉都没啥用，现在到了真正用Python代码实现二叉树的关键时刻了。我前面实现链表的时候就讲到了，Python中没有指针，采用一种类似指针的方式来实现结点，再有结点链接而成构成想要的数据结构，二叉树也不列外，每一个结点封装有数据，还有指向其左右子树的“指针”，然后其左右子树又有各自指向的左右子树，就这样构成了一个完整的二叉树结构。

二叉树结点的实现

是不是跟链表结点实现有那么一点异曲同工之妙啊，完全像是一个模子里面刻出来的一样。其实你知道了链表怎么实现，二叉树这些应该就不在话下了。So easy！

class Node(object):
    """二叉树结点"""
    def __init__(self, item):
        self.elem = item
        self.lchild = None
        self.rchild = None

二叉树的创建

这是一个空的二叉树，root是根节点。

class Tree(object):
    """二叉树"""
    def __init__(self):
        self.root = None

再给出具体添加节点元素代码之前，我们来大致复现一下添加结点元素的过程。在一个二叉树中添加结点，首先你要判断应该添加在哪里添加，二叉树是严格定义了结构的，一个根节点有且仅有一个左子树和一个右子树，要是根节点这里这里满了的话，我就不能在根节点的下面添加了，我要换到一个空的地方。

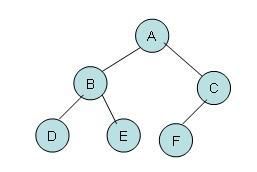
我拿这个二叉树做个例子：我们遍历的顺序定义为从上到下，从左到右（广度优先遍历），那么应该就是A B C D E F了，那么细节是怎么样的呢？
首先是根节点A，然后A的左结点B，A的右结点C (A B C)
A的左右都遍历完了，下面就是B的左右结点了，B作为根节点，B的左结点D，B的右结点E (B C D E)
B的左右都遍历完了，下面就是C的左右结点了，C作为根节点，C的左结点F，C没有右结点，那么添加的结点就应该放在这里。
然后你仔细看会发现，我每次从左边取出一个根节点，然后在右边添加他的左右结点，这种操作是不是很像一个队列的操作啊，只能从一边添加，然后另一边删除。我们就用队列的结构来实现二叉树。代码如下：

    def add(self, item):
    	# 将要添加的数据封装成一个node结点
        node = Node(item)
        # 判断是不是一个空树
        if self.root is None:
            self.root = node
            return
        #将根节点添加到队列中 
        queue = [self.root]
        # 如果队列不为空就一直遍历下去
        while queue:
        	# 取出队列里的第一个元素也就是根节点
            cur_node = queue.pop(0)
            # 判断左结点
            if cur_node.lchild is None:
                cur_node.lchild = node
                return
            else:
                queue.append(cur_node.lchild)
             # 判断右结点
            if cur_node.rchild is None:
                cur_node.rchild = node
                return
            else:
                queue.append(cur_node.rchild)

广度优先遍历

二叉树的创建时，遍历添加元素就是采用的广度优先遍历，又叫做层次遍历，一层一层的遍历二叉树。

    def breadth_travel(self):
        """广度遍历"""
        if self.root is None:
            return
        queue = [self.root]
        while queue:
            cur_node = queue.pop(0)
            print(cur_node.elem, end=" ")
            if cur_node.lchild is not None:
                queue.append(cur_node.lchild)
            if cur_node.rchild is not None:
                queue.append(cur_node.rchild)

先序、中序、后序遍历

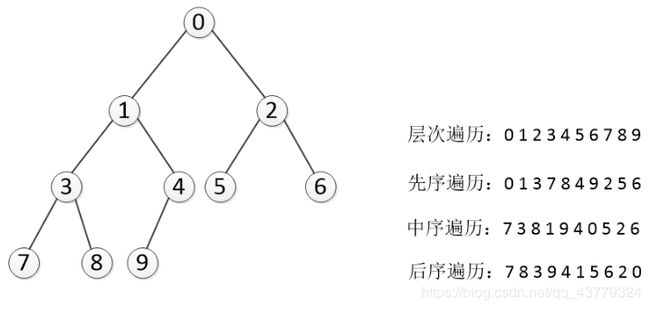
先序遍历就是先遍历根节点，然后左子树、右子树。
如图所示：首先是根节点0，然后我们将他左边的那一部分当成一个子二叉树也就是左子树，接着左子树的根节点是1；1的左子树是他左边下面的那一坨，根节点是3；3的左子树是7,7后面就没有了，然后右子树是8；我们以1为根节点的左边部分就遍历完了，接下来是其右子树，根节点是4；4的左子树是9，没有右子树，他们后面也啥也没有，以0为根节点的左边的部分就都遍历完了。然后遍历右子树，根节点是2；2的左右子树分别是56。
所以我们先序遍历的结果就是0 1 3 7 8 4 9 2 5 6
中序遍历是先遍历左子树，然后根节点，最后右子树。
如图所示：0作为根节点，左子树是左边那一大坨，然后根节点变成了1；1的左子树是以3为根节点，这是最小的完整二叉树分支了，那么按照先左后根再右的思路就应该是7 3 8;738作为一个完整的左子树，下一步就应该遍历他的根节点1；再就是右子树94，右子树的顺序是先9后4；整个大的左子树遍历完了，根节点是0；然后右子树256，遍历顺序是5 2 6。
所以我们中序遍历顺序是：7 3 8 1 9 4 0 6 2 5
后序遍历是先遍历左子树，然后右子树，最后根节点。
跟上面的方法一样，我们先抽丝剥茧，找到最小的左子树378，其遍历顺序是7 8 3；然后以1为根节点的右子树49，其遍历顺序是9 4；然后以0为根节点的右子树是256，其遍历顺序是5 6 2；最后就是根节点0.
所以我们中序遍历顺序是：7 8 3 9 4 1 5 6 2 0

接下来就应该是具体的代码实现了。我们前面讲到的这样一种抽丝剥茧的方式是不是有一点像函数里面的递归？根节点、左子树、左子树的根节点、左子树根节点的左子树…完全就像是一种递归的方式，一步步重复我们的方法。大家可以自己仔细想想，具体代码如下：

    def preorder(self, node):
        """先序遍历"""
        if node is None:
            return
        print(node.elem, end=" ")
        self.preorder(node.lchild)
        self.preorder(node.rchild)

    def inorder(self, node):
        """中序遍历"""
        if node is None:
            return
        self.inorder(node.lchild)
        print(node.elem, end=" ")
        self.inorder(node.rchild)

    def postorder(self, node):
        """后序遍历"""
        if node is None:
            return
        self.postorder(node.lchild)
        self.postorder(node.rchild)
        print(node.elem, end=" ")

测试代码：

if __name__ == "__main__":
    tree = Tree()
    tree.add(0)
    tree.add(1)
    tree.add(2)
    tree.add(3)
    tree.add(4)
    tree.add(5)
    tree.add(6)
    tree.add(7)
    tree.add(8)
    tree.add(9)
    tree.breadth_travel()
    print(" ")
    print("先序遍历：")
    tree.preorder(tree.root)
    print(" ")
    print("中序遍历：")
    tree.inorder(tree.root)
    print(" ")
    print("后序遍历：")
    tree.postorder(tree.root)
    print(" ")

后记

部分代码和图片来源于我学习的资料
Python实现二叉树是真的简单啊，感觉也没有花费很大的力气、也有可能是我太菜了叭！
有问题的地方欢迎大家指出！

新手上路，技术有限，不喜勿喷！