7-2 哈夫曼编码

7-2 哈夫曼编码

给定一段文字，如果我们统计出字母出现的频率，是可以根据哈夫曼算法给出一套编码，使得用此编码压缩原文可以得到最短的编码总长。然而哈夫曼编码并不是唯一的。例如对字符串"aaaxuaxz"，容易得到字母 ‘a’、‘x’、‘u’、‘z’ 的出现频率对应为 4、2、1、1。我们可以设计编码 {‘a’=0, ‘x’=10, ‘u’=110, ‘z’=111}，也可以用另一套 {‘a’=1, ‘x’=01, ‘u’=001, ‘z’=000}，还可以用 {‘a’=0, ‘x’=11, ‘u’=100, ‘z’=101}，三套编码都可以把原文压缩到 14 个字节。但是 {‘a’=0, ‘x’=01, ‘u’=011, ‘z’=001} 就不是哈夫曼编码，因为用这套编码压缩得到 00001011001001 后，解码的结果不唯一，“aaaxuaxz” 和 “aazuaxax” 都可以对应解码的结果。本题就请你判断任一套编码是否哈夫曼编码。

输入格式：

首先第一行给出一个正整数 N（2≤N≤63），随后第二行给出 N 个不重复的字符及其出现频率，格式如下：

c[1] f[1] c[2] f[2] ... c[N] f[N]

其中c[i]是集合{‘0’ - ‘9’, ‘a’ - ‘z’, ‘A’ - ‘Z’, ‘_’}中的字符；f[i]是c[i]的出现频率，为不超过 1000 的整数。再下一行给出一个正整数 M（≤1000），随后是 M 套待检的编码。每套编码占 N 行，格式为：

c[i] code[i]

其中c[i]是第i个字符；code[i]是不超过63个’0’和’1’的非空字符串。

输出格式：

对每套待检编码，如果是正确的哈夫曼编码，就在一行中输出"Yes"，否则输出"No"。

注意：最优编码并不一定通过哈夫曼算法得到。任何能压缩到最优长度的前缀编码都应被判为正确。

输入样例：

7
A 1 B 1 C 1 D 3 E 3 F 6 G 6
4
A 00000
B 00001
C 0001
D 001
E 01
F 10
G 11
A 01010
B 01011
C 0100
D 011
E 10
F 11
G 00
A 000
B 001
C 010
D 011
E 100
F 101
G 110
A 00000
B 00001
C 0001
D 001
E 00
F 10
G 11

输出样例：

Yes
Yes
No
No

解析

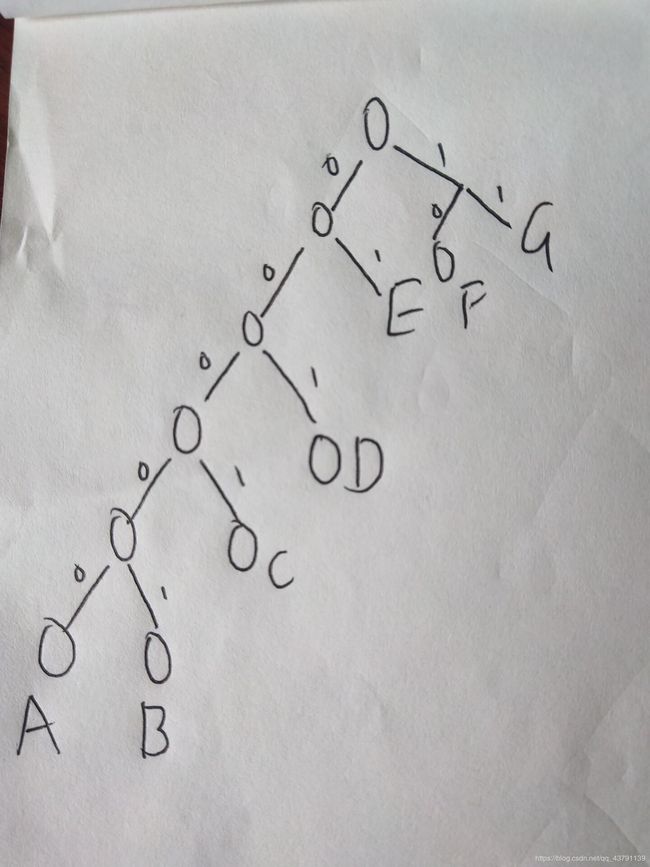
这样把树的结构画出来，左边为0右边为1，很容易看的出样例一是正确的。样例四中E为00，哈夫曼树根节点都是创建的，所以四是错误的

代码

#include
#include 
using namespace std;
int n;
struct knot{
	char name; //字符 
	int p;		//概率 
	int weight;	//长度 
	char code[65];  //编码 
}a[6400],in[63001];
typedef struct knoto{
	int parent;
	int lchild,rchild;
	int weight;		//概率 
}Create;
bool judge(int start,int end);
bool best(int start,int end);
void find(Create *self,int *x1,int *x2,int count);
int main(){
	int k;
	cin>>n;
	for(int i=0;i<n;i++){
		cin>>a[i].name>>a[i].p;
	}
	cin>>k;
	
	for(int i=0;i<k*n;i++){
		cin>>in[i].name>>in[i].code;
		in[i].p=a[i%n].p;
		in[i].weight=strlen(in[i].code);
		if(i%n==n-1){	//一组输入完毕,i是从0开始的 
			if(judge(i-n+1,i)&&best(i-n+1,i)){
				printf("Yes\n");
			}else{
				printf("No\n");
			}
		}
	}
	return 0;
} 
bool judge(int start,int end){ //此函数的功能是判断一组输入的编码是不是前缀编码，即在组内比较 
	for(int i=start;i<=end;i++){
		for(int j=start;j<=end;j++){
			if(i==j){	//如果是一个码，不用比 
				continue;
			}
			if(strlen(in[i].code)>strlen(in[j].code)){
				continue;
			}
			int k;
			for(k=0;k<strlen(in[i].code);k++){
				if(in[i].code[k]!=in[j].code[k]){
					break;
				}
			}
			if(k>=strlen(in[i].code)){//顺利结束，表明这不是前缀编码，即有重复 如例四中当i为E，j为A的时候
				return false;
			}
		}
	}
	return true;
}
//哈夫曼编造树，求加权最短路径看是否相等 
bool best(int start,int end){
	Create self[131];
	int it=0;	//输入的带权路径和 
	int m=2*n-1;
	for(int i=start;i<=end;i++){	//计算输入的带权路径和 
		it+=in[i].weight*in[i].p;
	}
	for(int i=0;i<n;i++){	//对已有的样本数据进行存储，静态实现，
		self[i].parent=self[i].rchild=self[i].lchild=-1;
		self[i].weight=in[i].p;
	}
	for(int i=n;i<m;i++){	//初始化空间
		self[i].parent=self[i].rchild=self[i].lchild=-1;
		self[i].weight=0;
	}
	int x1,x2;	//保存权值最小值和次小值的数组下标 
	for(int i=n;i<m;i++){
		find(self,&x1,&x2,i);
		self[i].lchild=x1;
		self[i].rchild=x2;
		self[i].weight=self[x1].weight+self[x2].weight;
		self[x1].parent=i;
		self[x2].parent=i;
	}
	int itt=0;
	for(int i=n;i<m;i++){
		itt+=self[i].weight;
	}
	if(it==itt)
		return true;
	else
		return false;
}
void find(Create *self,int *x1,int *x2,int count){
	int pmin=130,min=130;//需要保证节点不会累加到此处 
	self[min].weight=1000001;
	for(int i=0;i<count;i++){
		if(self[i].parent==-1&&self[i].weight<self[min].weight){
			pmin=min;
			min=i;
		}else if(self[i].parent==-1&&self[i].weight<self[pmin].weight){
			pmin=i;
		}
	}
	*x1=min;
	*x2=pmin;
}