【AcWing 110】 防晒 贪心 详解

有C头奶牛进行日光浴，第i头奶牛需要minSPF[i]到maxSPF[i]单位强度之间的阳光。

每头奶牛在日光浴前必须涂防晒霜，防晒霜有L种，涂上第i种之后，身体接收到的阳光强度就会稳定为SPF[i]，第i种防晒霜有cover[i]瓶。

求最多可以满足多少头奶牛进行日光浴。

输入格式
第一行输入整数C和L。

接下来的C行，按次序每行输入一头牛的minSPF和maxSPF值,即第i行输入minSPF[i]和maxSPF[i]。

再接下来的L行，按次序每行输入一种防晒霜的SPF和cover值,即第i行输入SPF[i]和cover[i]。

每行的数据之间用空格隔开。

输出格式
输出一个整数，代表最多可以满足奶牛日光浴的奶牛数目。

数据范围
1≤C,L≤2500,
1≤minSPF≤maxSPF≤1000,
1≤SPF≤1000
输入样例：
3 2
3 10
2 5
1 5
6 2
4 1
输出样例：
2

题意：如题

思路：

题意可转化成，数轴上存在若干区间，然后现在有若干种不同的数，每种数有若干个。现在要将这些数放进能放进的区间里面，问最大能使得多少个区间被填数（一次）
很自然的会想到贪心，让前面的区间尽量选择靠前的数，把大一点的数留给后面的区间。所以我们会选择把读入的区间存起来，排序，对于读入的每个单个数也是如此。但是，给区间排序的时候，必须是给右区间排序！！（WA了几发后的领悟）。为什么不是左端点排序，很简单，看下图：

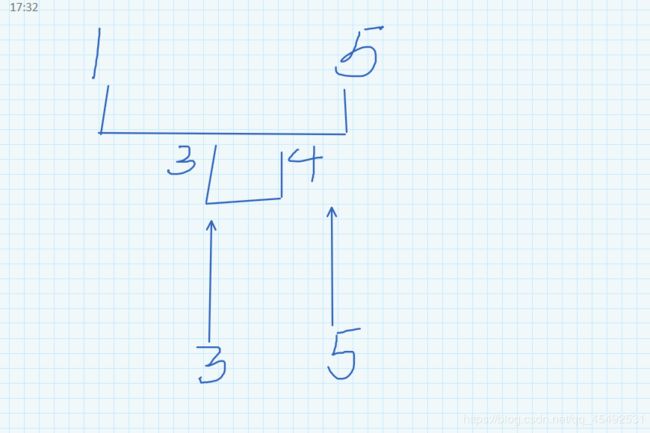
给一个【1,5】区间和【3,4】区间，有3和5这两个数各一个供选择。如果按照左端点排序，【1,5】这个区间会把3这个数给私吞了。然后【3,4】这个区间没数可选。然而【1,5】区间完全可以选择5这个数的，这就产生了WA点。而按照右端点排序，相当于优先把数给马上要超过范围的区间，这也是一种贪心。

AC代码：

#include
#include
#include
#include
#include
#include
#include
#include 
#include
#include 
#include 
#include 
#include
#define FAST ios::sync_with_stdio(false)
#define abs(a) ((a)>=0?(a):-(a))
#define sz(x) ((int)(x).size())
#define all(x) (x).begin(),(x).end()
#define mem(a,b) memset(a,b,sizeof(a))
#define max(a,b) ((a)>(b)?(a):(b))
#define min(a,b) ((a)<(b)?(a):(b))
#define rep(i,a,n) for(int i=a;i<=n;++i)
#define per(i,n,a) for(int i=n;i>=a;--i)
#define pb push_back
#define mp make_pair
#define fi first
#define se second
using namespace std;
typedef long long ll;
typedef pair<ll,ll> PII;
const int maxn = 5e5;
const int inf=0x3f3f3f3f;
const double eps = 1e-7;
const double pi=acos(-1.0);
const int mod = 1e9+7;
inline int lowbit(int x){return x&(-x);}
ll gcd(ll a,ll b){return b?gcd(b,a%b):a;}
void ex_gcd(ll a,ll b,ll &d,ll &x,ll &y){if(!b){d=a,x=1,y=0;}else{ex_gcd(b,a%b,d,y,x);y-=x*(a/b);}}//x=(x%(b/d)+(b/d))%(b/d);
inline ll qpow(ll a,ll b,ll MOD=mod){ll res=1;a%=MOD;while(b>0){if(b&1)res=res*a%MOD;a=a*a%MOD;b>>=1;}return res;}
inline ll inv(ll x,ll p){return qpow(x,p-2,p);}
inline ll Jos(ll n,ll k,ll s=1){ll res=0;rep(i,1,n+1) res=(res+k)%i;return (res+s)%n;}
inline ll read(){ ll f = 1; ll x = 0;char ch = getchar();while(ch>'9'||ch<'0') {if(ch=='-') f=-1; ch = getchar();}while(ch>='0'&&ch<='9') x = (x<<3) + (x<<1) + ch - '0',  ch = getchar();return x*f; }
int dir[4][2] = { {1,0}, {-1,0},{0,1},{0,-1} };

typedef struct Pos
{
    ll l;
    ll r;
} P;
P a[maxn];

typedef struct Val
{
    ll val;
    ll cnt;
    Val() {cnt=0;}
}V;

V b[maxn];

bool cmp(P a, P b)
{
    return a.r < b.r;
}

bool cmp1(V a, V b)
{
    return a.val < b.val;
}

int main()
{
    ll n,m;
    cin>>n>>m;
    rep(i,1,n) cin>>a[i].l>>a[i].r;
    rep(i,1,m) cin>>b[i].val>>b[i].cnt;
    sort(a+1,a+1+n,cmp);
    sort(b+1,b+1+m,cmp1);
    ll cur = 1;
    ll ans = 0;
    rep(i,1,n)
    {
        rep(j,1,m)
        {
            if(b[j].val>=a[i].l&&b[j].val<=a[i].r&&b[j].cnt)
            {
                b[j].cnt--;
                ans ++;
                break;
            }
        }
    }
    cout<<ans<<endl;
    return 0;
}