一、树和森林
1.基本概念
树状图(Tree)又称为树,是一种复杂的数据结构。树是由 n(n>=0)个有限节点组成一个具有层次关系的集合,把它叫做“树”是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。当 n=0 时,称之为空树,否则是非空树。
树具有以下的特点:
- 每个节点有零个或多个子节点;
- 没有父节点的节点称为根节点;
- 每一个非根节点有且只有一个父节点;
- 除了根节点外,每个子节点可以分为多个不相交的子树。
2.基本术语
子女:若节点的子树非空,则节点子树的根即为该节点的子女。
双亲:若节点有子女,则该节点即为子女的双亲。
兄弟:同一节点的子女互称为兄弟。
度:节点的子女个数即为该节点的度。
分支节点:度不为0的节点即为分支节点。
叶子节点:度为0的节点即为叶子节点。
深度:节点的深度即为该节点所在的层次。
高度:规定叶子节点的高度为1,其双亲节点的高度等于它的高度加1。
森林:森林是 m(m>=0)颗树的集合。
二、二叉树
1.基本概念
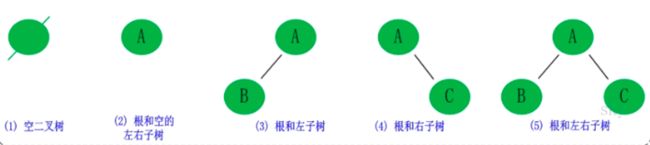
一颗二叉树是节点的有限集合,该集合或者为空,或者由一个根节点和两颗分别称为左子树和右子树的、互不交叉的二叉树组成(子树有左右之分,不可颠倒)。下面是二叉树的五种形态:
2.基本性质
性质1:若二叉树节点的层次从1开始,则在二叉树的第 i 层最多有 2i-1 个节点(i>=1)。
性质2:深度为 k 的二叉树最少有 k 个节点,最多有 2k-1个 节点(k>=1)。
性质3:对任意一颗二叉树,如果其叶子节点有 m 个,度为2的非叶子节点为 n 个,则有:m = n + 1。
设度为1的节点有 p 个,总节点数为 x,总边数为 e,则 x = m + n + p,e = n - 1 = 2 * n + p。因此有:
2 * n + p = m + n + p - 1
n = m - 1
m = n + 1
3.满二叉树和完全二叉树
1)满二叉树:除了最后一层无任何子节点,每一层的所有节点都有两个子节点,即除了叶子节点外的所有节点均有两个子节点,这样的二叉树就称为满二叉树。
2)完全二叉树:设一个二叉树的深度为 k,即共有 k 层。除了第 k 层外,其他各层的节点数都达到最大个数,且最后一层上只缺少右边的若干节点,这样的二叉树就称为完全二叉树。
4.Python 实现
下面是用 Python 实现的一个二叉树的代码,除了实现创建二叉树,还实现了四种遍历二叉树的方法,分别是:前序遍历、中序遍历、后序遍历和层次遍历。
1 # 自定义树节点
2 class Node:
3 def __init__(self, value=None, left=None, right=None):
4 self.value = value
5 self.left = left
6 self.right = right
7
8
9 # 自定义二叉树
10 class BinaryTree: 11 def __init__(self, value=None, left=None, right=None): 12 """ 13 根据传入的参数决定树的形态 14 :param value: 节点值 15 :param left: 左子树 16 :param right: 右子树 17 """ 18 self.root = Node(value, left, right) if value else None 19 20 def is_empty(self): 21 """ 22 判断是否为空树 23 :return: 24 """ 25 return True if self.root else False 26 27 def get_root(self): 28 """ 29 获取根节点 30 :return: 31 """ 32 return self.root 33 34 def get_left(self): 35 """ 36 获取左子树 37 :return: 38 """ 39 return self.root.left if self.root else None 40 41 def get_right(self): 42 """ 43 获取右子树 44 :return: 45 """ 46 return self.root.right if self.root else None 47 48 def set_left(self, node: Node): 49 """ 50 设置左子树 51 :param node: 树节点 52 :return: 53 """ 54 self.root.left = node 55 56 def set_right(self, node: Node): 57 """ 58 设置右子树 59 :param node: 树节点 60 :return: 61 """ 62 self.root.right = node 63 64 def pre_traverse(self, node: Node): 65 """ 66 前序遍历 67 :param node: 根节点 68 :return: 69 """ 70 if not node: 71 return 72 print(node.value, end=" ") 73 self.pre_traverse(node.left) 74 self.pre_traverse(node.right) 75 76 def mid_traverse(self, node: Node): 77 """ 78 中序遍历 79 :param node: 根节点 80 :return: 81 """ 82 if not node: 83 return 84 self.mid_traverse(node.left) 85 print(node.value, end=" ") 86 self.mid_traverse(node.right) 87 88 def after_traverse(self, node: Node): 89 """ 90 后序遍历 91 :param node: 根节点 92 :return: 93 """ 94 if not node: 95 return 96 self.after_traverse(node.left) 97 self.after_traverse(node.right) 98 print(node.value, end=" ") 99 100 def level_traverse(self, nodes: list): 101 next_nodes = [] 102 if nodes: 103 for node in nodes: 104 print(node.value, end=" ") 105 if node.left: 106 next_nodes.append(node.left) 107 if node.right: 108 next_nodes.append(node.right) 109 self.level_traverse(next_nodes)
当然光有这些方法还是不够的,因为要一个个的创建节点还是很麻烦,我们可以将一个树节点定义成一个三元组:
(树节点的值,左子树,右子树)
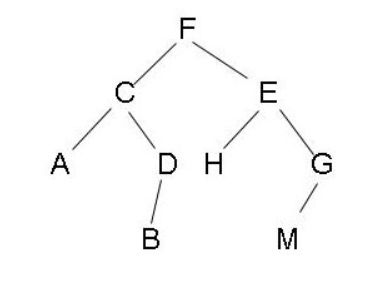
而左子树和右子树也都可以用这种三元组来表示,例如下面是一颗二叉树的三元组表示:
(F, (C, A, (D, B, None)), (E, H, (G, M, None)))
因此还需要实现一个将这种三元组表达形式转换成二叉树的方法:
1 def create(self, data: tuple):
2 """
3 创建一个二叉树
4 :param data: 例如(1,(2,4,5),(3,6,7))
5 """
6 self.root = self.parse(data)
7
8 def parse(self, data: tuple):
9 """
10 解析传入的三元组,创建二叉树
11 :param data: 三元组
12 :return:
13 """
14 if data:
15 node = Node(data[0])
16 node.left = self.parse(data[1]) if type(data[1]) == tuple else Node(data[1]) 17 node.right = self.parse(data[2]) if type(data[2]) == tuple else Node(data[2]) 18 return node
三、树的应用
1.表达式计算问题
1)问题描述
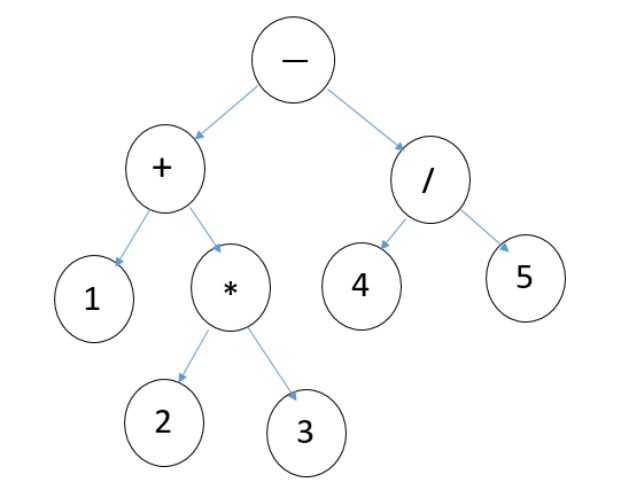
一个结构正确的二元表达式对应于一个满二叉树,例如下面这样一颗二叉树:
这样一颗二叉树前序遍历得到“-+1*23/45”,后序遍历得到“123*+45/-”,正是波兰表达式的形式,而其中序遍历结果就是“1+2*3-4/5”,基本就是相应数学表达式的正确形式,只是缺少了表达计算顺序的括号。输入一个简单的只包含四则运算的数学计算表达式,求出其计算后的结果。
2)问题分析
对于任意一个二元表达式(如“a+b”)都可以用一个三元组来表示(如“('+', a, b)”),而像上面示例中的表达式,就可以用下面这种三元组表示:
("-", ("+", 1, ("*", 2, 3)), ("/", 4, 5))
这种三元表达式都包含一个操作符设为 op,两个操作数分别为 x 和 y,因而可以写出下面的计算方法:
1 if op == "+":
2 return x + y
3 if op == "-":
4 return x - y
5 if op == "*":
6 return x * y 7 if op == "/": 8 return x / y if y else 0
那么现在的问题就是如何将数学表达式转换成二叉树,再就根据二叉树得到三元组,最后就能使用上面的方法把表达式的值求出来了。因为我们都知道在没有括号的情况下,乘除的优先级是高于加减的,而利用二叉树求解表达式时会从下往上,从叶子节点往根节点进行计算,所以要把加减号放在上面,乘除号放在下面。
3)二叉树求解
下面是根据输入的表达式字符串建立二叉树的具体代码:
1 def build_tree(input_string):
2 """
3 根据输入的表达式字符串建立二叉树
4 :param input_string: 输入表达式
5 :return:
6 """
7 if "+" in input_string or "-" in input_string:
8 for i in range(len(input_string)):
9 if input_string[i] in ["+", "-"] and "+" not in input_string[i + 1:] and "-" not in input_string[i + 1:]:
10 node = Node(input_string[i], build_tree(input_string[:i]), build_tree(input_string[i + 1:]))
11 return node 12 elif "*" in input_string or "/" in input_string: 13 for i in range(len(input_string)): 14 if input_string[i] in ["*", "/"]: 15 node = Node(input_string[i], build_tree(input_string[:i]), build_tree(input_string[i + 1:])) 16 return node 17 else: 18 return Node(input_string)
在生成二叉树之后,还要根据这个二叉树得到三元组,下面就是使用递归算法得到三元组的代码:
1 def trans(self, node: Node, data: tuple):
2 """
3 将二叉树转换成三元组
4 :param node: 节点
5 :param data: 三元组
6 :return:
7 """
8 left = self.trans(node.left, data) if node.left.left else node.left.value
9 right = self.trans(node.right, data) if node.right.left else node.right.value
10 data = (node.value, left, right)
11 return data
现在已经能生成二叉树并得到表达式的三元组了,再就是求值了,下面是使用递归算法计算三元表达式的值的代码:
1 def solution(e):
2 """
3 计算表达式的值
4 :param e: 转化成三元组表达的计算表达式
5 :return:
6 """
7 if type(e) == tuple:
8 op, a, b = e[0], solution(e[1]), solution(e[2])
9 x, y = float(a), float(b)
10 if op == "+":
11 return x + y 12 if op == "-": 13 return x - y 14 if op == "*": 15 return x * y 16 if op == "/": 17 return x / y if y else 0 18 else: 19 return e
求解计算表达式的代码已经完成了,下面是使用这些代码来求"1+2*3-4/5"的代码示例:
1 s = build_tree("1+2*3-4/5")
2 tree = Tree()
3 tree.root = s
4 exp = tree.trans(s, ())
5 print(solution(exp))
6 # 6.2