常见Normalization汇总

常见Normalization汇总

本文主要框架参考https://blog.csdn.net/liuxiao214/article/details/81037416，有许多自己的理解并进行了一定的删改，并且加上了PyTorch提供的各个Normalization的API。
其中，对于batchsize更详细的介绍可参考本人博客：https://blog.csdn.net/qyhaill/article/details/102463870

1 综述

1.1 论文链接

1. Batch Normalization
   https://arxiv.org/pdf/1502.03167.pdf
2. Layer Normalizaiton
   https://arxiv.org/pdf/1607.06450v1.pdf
3. Instance Normalization
   https://arxiv.org/pdf/1607.08022.pdf
   https://github.com/DmitryUlyanov/texture_nets
4. Group Normalization
   https://arxiv.org/pdf/1803.08494.pdf
5. Switchable Normalization
   https://arxiv.org/pdf/1806.10779.pdf
   https://github.com/switchablenorms/Switchable-Normalization

1.2 Normalization介绍

归一化层，目前主要有这几个方法：Batch Normalization（2015年）、Layer Normalization（2016年）、Instance Normalization（2017年）、Group Normalization（2018年）、Switchable Normalization（2018年）；

将输入的图像shape记为$[N,C,H,W]$，这几个方法主要的区别就是在：

• batchNorm是在batch上，对$NHW$做归一化，对小batchsize效果不好；
• layerNorm在通道方向上，对$CHW$归一化，主要对RNN作用明显；
• InstanceNorm在图像像素上，对$HW$做归一化，用在风格化迁移，因为在图像风格化中，生成结果主要依赖于某个图像实例，所以对整个batch归一化不适合图像风格化中，因而对$HW$做归一化。可以加速模型收敛，并且保持每个图像实例之间的独立；
• GroupNorm将channel分组，然后在每个group内做归一化；
• SwitchableNorm是将BN、LN、IN结合，赋予权重，让网络自己去学习归一化层应该使用什么方法。
  
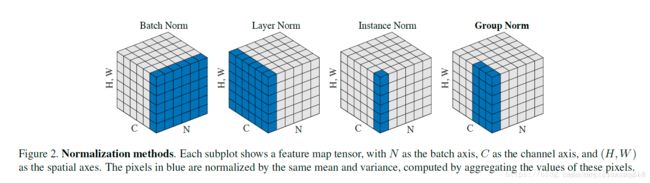
  从上图可以看出InstanceNorm是GroupNorm的极端情况。、

2 Batch Normalization

首先，在进行训练之前，一般要对数据做归一化，使其分布一致，但是在深度神经网络训练过程中，通常以送入网络的每一个batch训练，这样每个batch具有不同的分布；此外，为了解决internal covarivate shift问题在训练过程中，数据分布会发生变化，对下一层网络的学习带来困难。这个问题定义也是在Batch Normalizaiton这篇论文提出的。
Batch Normalization就是强行将数据拉回到均值为0，方差为1的正太分布上，这样不仅数据分布一致，而且避免发生梯度消失。
此外，internal corvariate shift和covariate shift是两回事，前者是网络内部，后者是针对输入数据，比如我们在训练数据前做归一化等预处理操作。

2.1 算法过程

• 沿着通道计算一个batch的每个channel的均值 ${\mu }^c$和方差，其中$n=\{1,...,N\},c=\{1,...,C\},h=\{1,...,C\},w=\{1,...,W\}$：
  $${\mu }^c=\frac{1}{NHW}\sum _{n=1}^N\sum _{h=1}^H\sum _{w=1}^W{x}_{nhw}^c，{\sigma }^c=\sqrt{\frac{1}{NHW}\sum _{n=1}^N\sum _{h=1}^H\sum _{w=1}^W(x_{nhw}^c-{\mu }^c{)}^2}$$
  其中，${\mu }^c$和${\sigma }^c$表示这个batch的第$c$个channel的所有maps的所有值的均值和方差，$x_{nhw}^c$表示这个batch的第$c$个channel的第$n$个实例所对应的map在$(h,w)$处的值。
• 然后做归一化并加入缩放和平移变量$\gamma$和$\beta$ ：
  $$y_{nhw}^c=\frac{x_{nhw}^c-{\mu }^c}{\sqrt{{\sigma }^c+ϵ}}\ast \gamma +\beta$$
  其中，$y_{nhw}^c$表示这个batch归一化并仿射后的第$c$个channel的第$n$个实例所对应的map在$(h,w)$处的值。

加入缩放平移变量的原因是：保证每一次数据经过归一化后还保留原有学习来的特征，同时又能完成归一化操作，加速训练。 这两个参数是用来学习的参数。

2.2 pytorch的Batch Normalization

class torch.nn.BatchNorm1d(num_features, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
class torch.nn.BatchNorm2d(num_features, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
class torch.nn.BatchNorm3d(num_features, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)

参数：

1. num_features：即输入的channel；
2. eps：就是计算公式中的$ϵ$，为保证数值稳定性（分母不能趋近或取0），给分母加上的值，默认为$1e-5$；
3. momentum：这个参数很多博客都解释错了，上文我们讲过BN在test时没有batch，无法计算均值和标准差，实际的做法是将训练过程中每轮的均值和标准差保存下来，然后按权相加，得到test时使用的均值和标准差。而momentum表示的就是权值。计算过程如下：
   假设$\hat{x}$是test时的均值或标准差，
   1. 第一轮的的$\hat{x}$就是这一轮训练数据计算出的statistic；
   2. 第二轮到最后一轮的每一轮，假设第$t$轮的statistic为$x_t$，$\hat{x}$都按公式${\hat{x}}_{\text{new}}=(1-\text{momentum})\times \hat{x}+\text{momentum}\times x_t,\hat{x}={\hat{x}}_{new}$ 进行更新；
4. affine：默认为True。当设为True时，使normalization后的均值和标准差（缩放变量$\gamma$和和平移变量$\beta$）设置为可学习的参数；否则为0和1。缩放加平移就是仿射，affine的意思就是仿射。

pytorch中BN的公式：

$$y=\frac{x-\mathrm{E}[x]}{\sqrt{\mathrm{V}\mathrm{a}\mathrm{r}[x]+ϵ}}\ast \gamma +\beta$$

3. Layer Normalization

batch normalization存在以下缺点：

• 对batchsize的大小比较敏感，由于每次计算均值和方差是在一个batch上，所以如果batchsize太小，则计算的均值、方差不足以代表整个数据分布；
• BN实际使用时需要计算并且保存某一层神经网络batch的均值和方差等统计信息，对于对一个固定深度的前向神经网络（DNN，CNN）使用BN，很方便；但对于RNN来说，sequence的长度是不一致的，换句话说RNN的深度不是固定的，不同的time-step需要保存不同的statics特征，可能存在一个特殊sequence比其他sequence长很多，这样training时，计算很麻烦。（参考于https://blog.csdn.net/lqfarmer/article/details/71439314）

3.1 算法过程

• 与BN不同，LN是针对深度网络的某一层的所有神经元的输入按以下公式进行normalize操作，其中$n=\{1,...,N\},c=\{1,...,C\},h=\{1,...,C\},w=\{1,...,W\}$：
  $${\mu }^n=\frac{1}{CHW}\sum _{c=1}^C\sum _{h=1}^H\sum _{w=1}^W{x}_{chw}^n，{\sigma }^n=\sqrt{\frac{1}{CHW}\sum _{c=n}^C\sum _{h=1}^H\sum _{w=1}^W(x_{chw}^n-{\mu }^n{)}^2}$$
  其中，${\mu }^n$和${\sigma }^n$表示某一层输出的第n个实例对应的feature maps的均值和方差，$C\ast H\ast W$是这一层神经元的个数，即这一层输出的feature maps共有多少个值，$x_{chw}^n$表示这一层输出的第n个实例对应的feature maps的第$c$个map上$(h,w)$位置的值。
• 然后做归一化并加入缩放和平移变量$\gamma$和$\beta$ ：
  $$y_{chw}^n=\frac{x_{chw}^n-{\mu }^n}{\sqrt{{\sigma }^n+ϵ}}\ast \gamma +\beta$$
  其中，$y_{chw}^n$是这一层输出的第n个实例对应的feature maps归一化并仿射后在第$c$个map上$(h,w)$位置的值。

3.2 BN和LN的区别

• LN中同层神经元输入拥有相同的均值和方差，不同的输入样本有不同的均值和方差；
• BN中则针对不同神经元输入计算均值和方差，同一个batch中的输入拥有相同的均值和方差。

所以，LN不依赖于batch的大小和输入sequence的深度，因此可以用于batchsize为1和RNN中对边长的输入sequence的normalize操作。

LN用于RNN效果比较明显，但是在CNN上，不如BN。

3.3 pytorch的Layer Normalization

class torch.nn.LayerNorm(normalized_shape, eps=1e-05, elementwise_affine=True)

参数：

1. normalized_shape： 输入尺寸，可以是int或list；
2. eps：就是计算公式中的$ϵ$，为保证数值稳定性（分母不能趋近或取0），给分母加上的值，默认为$1e-5$；
3. elementwise_affine： 布尔值，当设为true，给该层添加可学习的仿射变换参数$\gamma$和$\beta$。

pytorch中LN的公式：

$$y=\frac{x-\mathrm{E}[x]}{\sqrt{\mathrm{V}\mathrm{a}\mathrm{r}[x]+ϵ}}\ast \gamma +\beta$$

4 Instance Normalization

BN注重对每个batch进行归一化，保证数据分布一致，因为判别模型中结果取决于数据整体分布。

但是图像风格化中，生成结果主要依赖于某个图像实例，所以对整个batch归一化不适合图像风格化中，因而对HW做归一化。可以加速模型收敛，并且保持每个图像实例之间的独立。

在计算上可以将IN看做$batchsize=1$的BN。

4.1 算法过程：

• IN首先对每个实例$HW$维度求均值和标准差，其中$n=\{1,...,N\},c=\{1,...,C\},h=\{1,...,C\},w=\{1,...,W\}$：
  $${\mu }^{nc}=\frac{1}{HW}\sum _{h=}^H\sum _{w=1}^W{x}_{hw}^{nc}，{\sigma }^{nc}=\sqrt{\frac{1}{HW}\sum _{h=1}^H\sum _{w=1}^W(x_{hw}^{nc}-{\mu }^{nc}{)}^2}$$
  其中，${\mu }^{nc}$和${\sigma }^{nc}$表示这个batch中的第$n$个实例对应的feature maps中的第$c$个map所有值的均值和方差，$x_{hw}^{nc}$表示这个batch的第$n$个实例对应的feature maps中的第$c$个map在$(h,w)$位置的值。
• 然后做归一化并加入缩放和平移变量$\gamma$和$\beta$ ：
  $$y_{hw}^{nc}=\frac{x_{hw}^{nc}-{\mu }^{nc}}{\sqrt{{\sigma }^{nc}+ϵ}}\ast \gamma +\beta$$
  其中，$y_{hw}^{nc}$表示这个batch的第$n$个实例对应的feature maps归一化并仿射后的第$c$个map在$(h,w)$位置的值。

4.2 pytorch中的Instance Normalization

class torch.nn.InstanceNorm1d(num_features, eps=1e-05, momentum=0.1, affine=False, track_running_stats=False)
class torch.nn.InstanceNorm2d(num_features, eps=1e-05, momentum=0.1, affine=False, track_running_stats=False)
class torch.nn.InstanceNorm3d(num_features, eps=1e-05, momentum=0.1, affine=False, track_running_stats=False)

参数：

1. num_features：即输入的channel；
2. eps：就是计算公式中的$ϵ$，为保证数值稳定性（分母不能趋近或取0），给分母加上的值，默认为$1e-5$；
3. momentum：这个参数很多博客都解释错了，上文我们讲过BN在test时没有batch，无法计算均值和标准差，实际的做法是将训练过程中每轮的均值和标准差保存下来，然后按权相加，得到test时使用的均值和标准差。而momentum表示的就是权值。计算过程如下：
   假设$\hat{x}$是test时的均值或标准差，
   1. 第一轮的的$\hat{x}$就是这一轮训练数据计算出的statistic；
   2. 第二轮到最后一轮的每一轮，假设第$t$轮的statistic为$x_t$，$\hat{x}$都按公式${\hat{x}}_{\text{new}}=(1-\text{momentum})\times \hat{x}+\text{momentum}\times x_t,\hat{x}={\hat{x}}_{new}$ 进行更新；
4. affine：默认为False。当设为True时，使normalization后的均值和标准差（缩放变量$\gamma$和平移变量$\beta$）设置为可学习的参数；否则为0和1。缩放加平移就是仿射，affine的意思就是仿射。

pytorch中的IN公式：

$$y=\frac{x-\mathrm{E}[x]}{\sqrt{\mathrm{V}\mathrm{a}\mathrm{r}[x]+ϵ}}\ast \gamma +\beta$$

5 Group Normalization

主要是针对Batch Normalization对小batchsize效果差，GN将channel方向分group，然后每个group内做归一化，算$(C//G)\ast H\ast W$的均值，这样与batchsize无关，不受其约束。

GN计算均值和标准差时，把每一个实例的 feature maps 的 channel 分成G组，每组将有 $C//G$ 个 channel，然后将这些 channel 中的元素求均值和标准差。各组 channel 用其对应的归一化参数独立地归一化。

5.1 算法过程：

• 对于某个channel组（假设这个组包含的feature maps是从第$g(C//G)$个map到第$(g+1)(C//G)-1$个map），首先计算这个channel组中的均值和方差，其中$g=\{0,...,G-1\},n=\{1,...,N\},c=\{1,...,C\},h=\{1,...,C\},w=\{1,...,W\}$：
  $${\mu }^{ng}=\frac{1}{(C//G)HW}\sum _{c=g(C//G)}^{(g+1)(C//G)}\sum _{h=1}^H\sum _{w=1}^W{x}_{chw}^{ng},{\sigma }^{ng}=\sqrt{\frac{1}{(C//G)HW}\sum _{c=g(C//G)}^{(g+1)(C//G)}\sum _{h=1}^H\sum _{w=1}^W(x_{chw}^{ng}-{\mu }^{ng}{)}^2}$$
  其中，${\mu }^{ng}$和${\sigma }^{ng}$分别是这个batch中第$n$个实例对应的feature maps的第$g$个channel组的均值和方差，$x_{chw}^{ng}$表示这个batch中第$n$个实例对应的feature maps的第$g$个channel组包含的第$c$个map在$(h,w)$位置的值。
• 然后做归一化并加入缩放和平移变量$\gamma$和$\beta$ ：
  $$y_{chw}^{ng}=\frac{x_{chw}^{ng}-{\mu }^{ng}}{\sqrt{{\sigma }^{ng}+ϵ}}\ast \gamma +\beta$$
  其中，$y_{chw}^{ng}$表示这个batch中第$n$个实例对应的feature maps归一化并仿射后的第$g$个channel组包含的第$c$个map在$(h,w)$位置的值。

5.2 pytorch中的Group Normalization

class torch.nn.GroupNorm(num_groups, num_channels, eps=1e-05, affine=True)

参数：

1. num_groups：需要划分的channel组个数；
2. num_features：即输入的channel；
3. eps：就是计算公式中的$ϵ$，为保证数值稳定性（分母不能趋近或取0），给分母加上的值，默认为$1e-5$；
4. affine：默认为True。当设为True时，使normalization后的均值和标准差（缩放变量$\gamma$和平移变量$\beta$）设置为可学习的参数；否则为0和1。缩放加平移就是仿射，affine的意思就是仿射。

pytorch中的GN公式：

$$y=\frac{x-\mathrm{E}[x]}{\sqrt{\mathrm{V}\mathrm{a}\mathrm{r}[x]+ϵ}}\ast \gamma +\beta$$

6 Switchable Normalization

• 归一化虽然提高模型泛化能力，然而归一化层的操作是人工设计的。在实际应用中，解决不同的问题原则上需要设计不同的归一化操作，并没有一个通用的归一化方法能够解决所有应用问题；
• 一个深度神经网络往往包含几十个归一化层，通常这些归一化层都使用同样的归一化操作，因为手工为每一个归一化层设计操作需要进行大量的实验。