原创:搜索算法之两个数组取交集的算法
在垂直搜索中,有很多方法可以控制返回结果的数量。比如用户输入"上海世博会",要求只显示跟上海世博会相关的内容。有三种方法可以参考:①BooleanQuery,AND逻辑②phraseQuery,精读最高,只出现"上海世博会"连续的短语的文档③solr的模糊匹配查询。如果采用第一种方案,在垂直搜索中(比如Lucene),如果用户的查询向量(经由queryParser处理,调用中文分词,并且形成查询语法树)Term t = {xx,xx,……},BooleanQuery为AND时,向量中每一个维度的元素得到对应的倒排列表,倒排列表由许多的倒排索引项构成,然后取其中有交集的文档编号,然后进行排序。其核心思想类似于如下问题:
现有两个数组:int []data1 = {12,45,65,2,5} int []data2 = {12,5,-8,9},取其中的交集。
关于这个算法,最主要的精力是放在如何降低时间复杂度上。采取先排序再找交集的算法或者以空间换时间的算法,都不可取,要么时间复杂度高,要么就是空间复杂度高。Lucene源代码里,采用的是先排序,然后定义两个指针开始搜索相同的数字。当容量非常大时,这个算法的性能其实是不太好的。如果采用quickSort,最坏的复杂度是n^2,平均复杂度是nlgn。如果容量超过1千万,mergeSort会好一点,最坏复杂度为nlgn。大量的时间将浪费在排序上。换个思路,对于数字的处理,既然取交集,不妨从整体着手,避免一开始就陷入局部讨论。急于算法的实施,效果反而不好。对于不同的问题,要善于从整体考虑,分析内部的规律。那就要学会观察,类比和迁移,学会演绎推理。对于一个问题的解决,可以从一个类似的比较简单的事物入手,找出规律,然后进行迁移,改进,做近一部的研究。很多程序员都会各种排序算法,比如mergeSort,quickSort,HeapSort and son on。一开始进行排序,可能是程序员的惯性思维。对于这个算法,如果你的第一想法是它的话,说明你在算法上,还有提升空间,思维方式需要改变。解决一个问题,最忌讳的就是思维定势。经验有好处也有坏处。正确的做法是,忘记储备的知识,采用最原始的手段,从研究表象入手,寻找内部的规律,然后用理论验证。其次,进行迁移,演化。单独从排序算法来看的话,如果数据量<1000w的话,quickSort性能会好一些,达到上亿级别的,mergeSort会好一些。如果给你一个海量数据,要求寻找出topK最大值或者最小值来,采用排序当然能解决。因为抛开问题本身,单独来看,mergeSort可能是最好的。但是,对于这个问题,性能却是十分拙劣的。所以说,没有绝对好的算法。抛开应用场景的算法,即使是好的,最后也可能是拙劣的。这个问题的着手点,可以从下面开始:
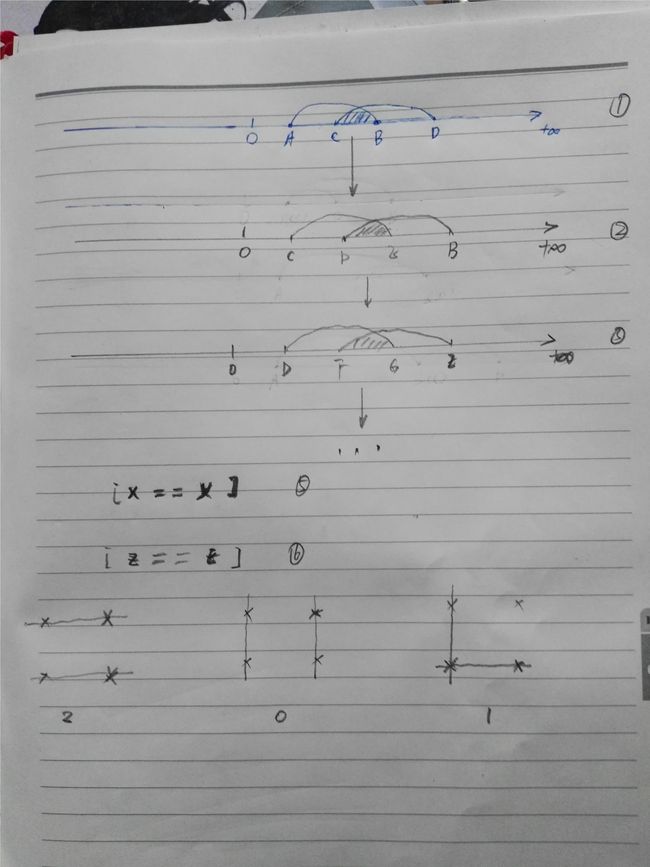
对于数字取交集,可以画一个数轴,先从简单的连续型数字入手,然后再迁移到离散型的数字。看下图:
对于图中的①,A~B,C~D为两个数组的取值范围,交集就是CB部分。如果两个数组中的数字是连续型的,那么,CB就是结果,非常简单。但是,大部分数组是离散型的数字。CB里面的数字,只有一部分是想要的结果。需要对CB进行进一步的处理。很容易想到的是,把AC和BD部分砍掉,对剩余的CB部分进行相同的处理,如图中的②和③。在这个过程中,每次找相同的数字,都是从只有两个数字(取值范围)的集合中寻找,之后两个数组只保留取值范围的交集部分,然后不断循环,大大降低了时间和空间复杂度这个算法本身并不难,但是,如何从两个取值范围的数组里寻找相同的值,(从AB和CD里找),如何判断算法何时收敛,需要耐心地寻找规律,逻辑分类要清晰,经得起各种等价值和边界值的测试,保证算法准确无误,可能要花费一些时间。整理起来,思路大致如下:
即:1.分别计算两个数组的min和max(取值范围),加入到rangeList 中,然后计算rangeLis中重复的数值,加入到result(list)中;
2.计算rangeList的取值范围交集,比如[1,20,3,15],两个数组的取值范围交集为[3,15],放在数组中,然后根据这个交集分别去除两个数组中不在此范围内的数值,清空rangeList,清零数组;
3.重复上述步骤,直到符合终止条件位置。
从取值范围中寻找相同值以及算法收敛条件:
寻找相同值的过程中,要注意收敛条件的判断,所以比较好的思路是:把两个取值范围加到一个集合中,再把这四个数字加到set中,分别求和,然后根据set的size大小辅助判断。和值sum1和sum2分别为第一个集合和set的和值。①size == 1:把结果加载到结果集中,算法收敛;
②size == 3:说明有一对数字重复。重复的数字分布情况有两种:一是分别分布在两个数组中;二是全部分布在一个数组中,这种情况,直接返回结果,算法收敛;对于第一种情况,sum1 - sum2就是相同的数值,加载到结果集中,继续后面的处理。
③size == 2:说明有两组数字重复,分布情况如第一张图的下面部分,2代表矩阵两行相等,0代表矩阵两列相等,1代表一行一列各相等。如果是2的话,直接返回结果,算法收敛;如果是0的话,set本身就是相同的数值。
④size == 4:有两种情况,其中一种是两个压缩集合没有交集,在后面的代码中应该增加收敛判断条件,如果有交集,直接进行后面的处理。
在这个迭代过程中,循环终止的整体条件是:两个数组中有任何一个size == 0或者取值范围的交集倒置。
通过不断减少数组的元素个数,动态控制迭代次数,迭代次数大大降低,当容量非常大时,会显示出优越的性能。此为目前最优的算法。
以上是逻辑实现,最重要的还是数据结构,由于在这个过程中,会不断地去除数组中的数值,所以底层采用链式存储的线性表,性能会比较高。
经过调试后,准确无误,现在上传代码,以供分享:
package com.txq.test;
import java.util.List;
import java.util.ArrayList;
import java.util.Collection;
import java.util.Collections;
import java.util.HashSet;
import java.util.Iterator;
import java.util.Queue;
import java.util.Set;
import java.util.concurrent.ConcurrentLinkedDeque;
/**
* 两个数组取交集算法,优于先排序后搜索的算法
* @author XueQiang Tong
* @date 2017/10/21
*/
public class IntersectionForPairArray {
private List inter = new ArrayList(4);//存储压缩后的集合
private Set s = new HashSet(4);//过滤压缩集合中的重复数字
private Queue arr1 = new ConcurrentLinkedDeque();//存储原始数据的队列,链式存储
private Queue arr2 = new ConcurrentLinkedDeque();
private List result = new ArrayList();//结果集
private List intersec = new ArrayList(2);//压缩集合的交集
public List intersection(int[]ar1,int[]ar2){
if(ar1.length == 0 || ar2.length == 0 || ar1 == null || ar2 == null) return result;
//1.把数据加载到队列中
int len = Math.max(ar1.length, ar2.length);
for (int i = 0;i < len;i++){
if (i <= ar1.length-1){
arr1.add(ar1[i]);
}
if (i <= ar2.length-1){
arr2.add(ar2[i]);
}
}
while(true) {
//2.集合压缩
inter.add(Collections.min(arr1));
inter.add(Collections.max(arr1));
inter.add(Collections.min(arr2));
inter.add(Collections.max(arr2));
for (int i = 0;i < inter.size();i++){//把压缩后的集合加入到set中
s.add(inter.get(i));
}
int size = s.size();
//下面开始寻找相同的数字
if(size == 4){
}
//先求和
int sum = computeSum(inter);
int sum1 = computeSum(s);
int res = sum - sum1;
if (size == 3){
if ((inter.get(0) == inter.get(1)) || (inter.get(2) == inter.get(3))){
return result;
}
else {
result.add(res);
arr1.remove(res);
arr2.remove(res);
}
}
if (size == 2) {//有三个元素和两对儿元素重复的情况,收敛情况是两个压缩集合各自重复,三个元素重复的情况其结果是res/2
if ((inter.get(0) == inter.get(1)) && (inter.get(2) == inter.get(3))) {
return result;
}
else {
if((inter.get(0) == inter.get(2)) && (inter.get(1) == inter.get(3))){
result.addAll(s);
for (int element:s){
arr1.remove(element);
arr2.remove(element);
}
} else {
result.add(res/2);
arr1.remove(res/2);
arr2.remove(res/2);
}
}
}
if (size == 1) {
result.addAll(s);
return result;
}
//4.计算inter的交集,并分别去除两个集合中不在此范围内的元素
intersec.add(Math.max(inter.get(0),inter.get(2)));
intersec.add(Math.min(inter.get(1),inter.get(3)));
if (intersec.get(0) > intersec.get(1)) break;//当size == 4并且两个压缩集合没有交集时,到此终止
removeElement(arr1);
removeElement(arr2);
if (arr1.size() == 0 || arr2.size() == 0) break;
s.clear();
inter.clear();
intersec.clear();
}
return result;
}
private void removeElement(Queue queue) {
Iterator it = queue.iterator();
while (it.hasNext()){
int n = it.next();
if (n < intersec.get(0) || n > intersec.get(1)) {
queue.remove(n);
}
}
}
private int computeSum(Collection col) {
int sum = 0;
for (int i :col){
sum += i;
}
return sum;
}
}
数据结构,底层就两种,一为顺序存储的散列结构,另一个为链式结构struct。第一种结构,在搜索方面有优势,另一个在存储空间及增删改方面有优势。利用这两种数据结构,结合数据安全(比如CAS算法,多线程)和算法,可以根据业务需求设计出更加复杂的数据结构,比如三叉树,哈夫曼树,红黑树,堆 and so on。平时使用现成的库里的数据结构,比如map,set等等,底层都是基于上述两种结构。不同的结构,有不同的优势。比如,solr内部自置的搜索智能提示功能,数据结构采用三叉树。三叉树的优势是树中有树,能够节省内存空间,但是在查找方面,不及平衡的二叉树。所以,在构建三叉树的时候,采用了折中处理,以提高搜索时间。设计平衡的二叉树,就是要解决时间和空间问题,所以底层数据结构,才采用struct(封装对象属性和指针的类)。