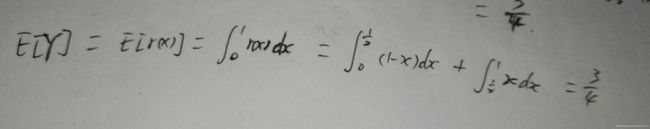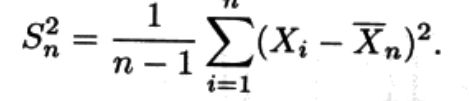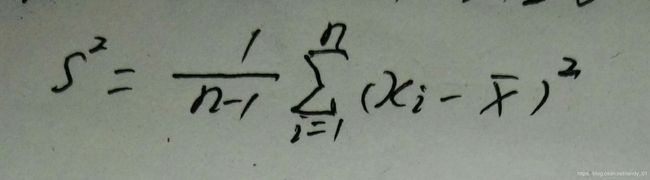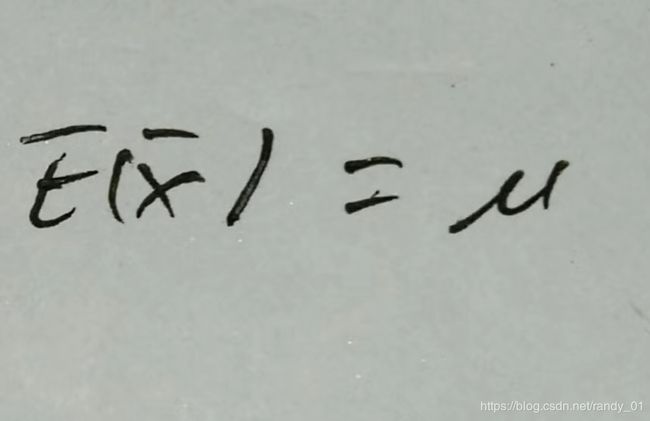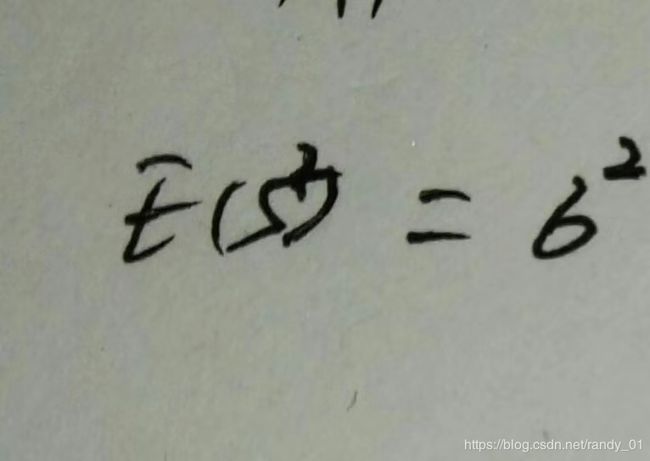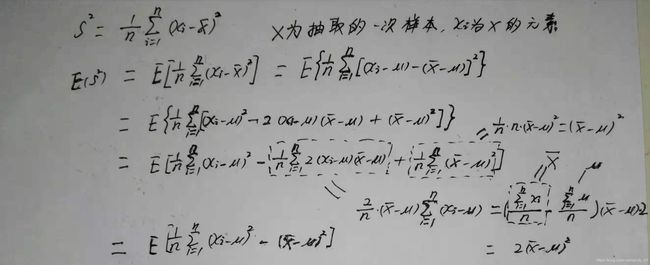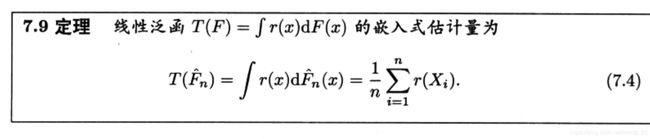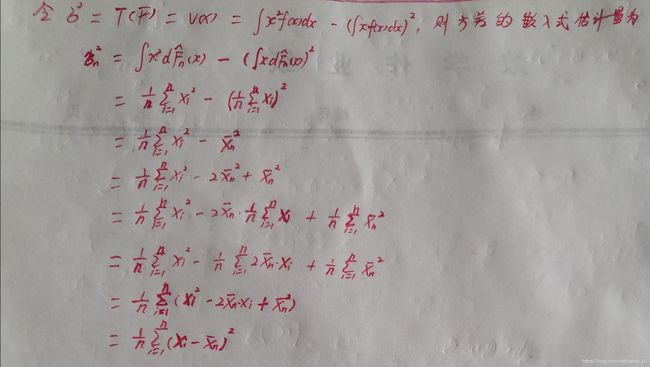统计学笔记(二)

前言：本篇博客包括了随机变量和图模型推理之间的所有内容。学好《统计学》需要《微积分》，《线性代数》，《矩阵论》和《实变函数与泛函数分析》作为基础，另外再增加《凸优化》。如果只是应用的话，这些知识吸收60%就足够了，但是要搞研究的话，不仅要吸收80%以上，另外还要研究《神经生物学从神经元到大脑》和物理学，从中吸收灵感，为研究下一代AI打下好的基础，用几何问题解决代数问题是不可避免的。下一代AI的突破点在nlp推理，人脑对于文字的神经元理解机制目前需要突破，最大限度地减少对海量数据的依赖。本文结构安排如下：

一、数学期望和不等式：这部分主要介绍期望，方差，协方差，协方差和皮尔逊相关系数的本质区别，高斯分布的矩母函数以及概率不等式，另外还增加了凹凸函数的不等式；

二、随机变量的收敛，单独作为一部分，重点是中心极限定理(和高斯分布相关)；

三、参数估计前的准备以及最大似然估计，包括：①模型，统计推断与学习的概念②CDF和统计泛函的估计③Bootstrap方法，接下来是最大似然估计，包括：①矩估计②极大似然估计以及相合性和同变性③渐进性④delta方法

后续安排：下一篇博客开始介绍图模型：从有向图到无向图的所有内容：贝叶斯，朴素贝叶斯，贝叶斯网格，有向动态图模型HMM，ME，MEMM，CRF(linear chain)，BiLSTM_CRF，pageRank算法，拉普拉斯矩阵，其中会穿插着介绍《统计学》的知识，所以篇幅会非常长。然后第四篇博客开始系统介绍深度学习，主要包括：①BP算法②RNN到LSTM的演化过程③卷积算子④深度学习的优化，算法本身的改进⑤语义表示和相似度，包括SIF，w2v,siamese lstm。⑥参数优化：SGD与遗传算法和模拟退火。紧接着第五篇博客会整合统计学派和联结主义学派，重点论述无向图推理,有向图推理，GN block。第六篇博客介绍知识图谱向量化(transD以及改进1篇)以及和深度学习的融合。以上工作全部完成后从第七篇博客开始，系列介绍与业务相关的Ai，包括kb_qa系列(共5篇)，模板匹配问答(1篇)，slot对话。

以上全部完成后，开始研究《神经生物学从神经元到大脑》和本体论，今后的全部精力用于研究专家系统和语义网。

nlp理论创新的研究既需要广度又需要深度，经历了前期的积累和摸索整合后，后期会形成稳定的研究课题。拒绝搞套路，拒绝刷题搞应试教育糊弄人，拒绝走捷径。走所谓的捷径就是走弯路。沉下心来，避免急功近利和浮躁。脱离应用级别的研究很不容易，希望码农们能转型顺利：站在巨人的肩膀上，强大的整合能力是成功的保证！

一、数学期望和不等式

1.1 期望

1.11 概念

 律。为了更好地理解期望的含义，先看几个例子：

 懒惰统计学家法则:

 下面引入一个例子，来运用懒惰统计学家法则，引入之前先回顾一下均匀分布：

均匀分布其实就是CDF的变化是均匀的，比如对于离散变量，累计概率值可以是等差数列，这样的变化就是均匀的，而他的导函数就是常量了。如下：

 如果x的取值范围为[0,1],概率密度函数f(x) = 1。

题目：将一根单位长度的棍子从中间某一点折断,令Y表示剩下的较长的一段，问Y的期望是多少？

分析：对于概率问题，首先要确定随机变量，然后确定变量的分布类型，这两步做好了后就可以运用法则求解了。首先，确定随机变量，很明显随机变量是棍子的位置点X，取值范围为[0,1],这个点是线性的，所以是均匀变化的，因此是均匀分布。那么他的概率密度函数f(x) = 1。下面定义Y: Y = max{X,1 - X}

 

1.12 性质

 1.2 方差、协方差与皮尔逊相关系数

 1.21 方差

 

 

 个人总结：概率密度衡量了变量的区域概率质量分布情况，比如在这个区域内概率质量比较大，另一个区域概率质量比较小，或者在所有的区域内概率质量均匀分布(uniform分布)。方差衡量了样本总体偏离均值的波动情况，方差越大，波动越大。

补充：看了前面的内容后肯定有个疑惑：我们发现总体的均值和方差与样本的均值和方差有些不同。样本的方差为何除以n-1而不是n?这里面有很学问，下面进行解释： 

设总体均值和方差为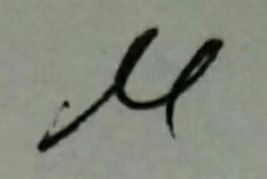 、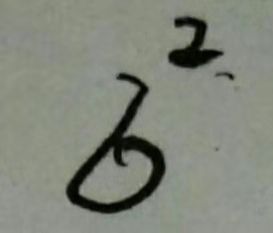，样本的均值的方差为 、。那么样本方差的公式为：

    

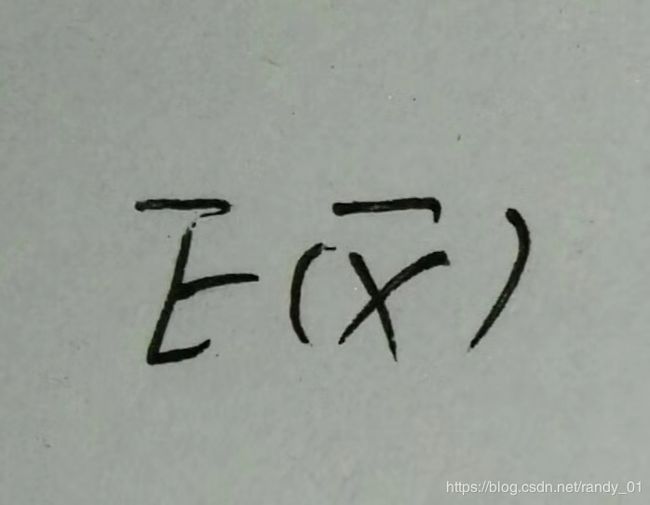我们在抽取样本估计的时候是从总体中抽取一部分进行估计均值和方差，那么样本的均值和方差和总体之间就有了误差 。比如一次抽取200个作为样本统计均值和方差，为了尽量减少误差我们会多次随机抽取200个样本，这样就得到了一系列均值和方差，然后我们再以这些均值和方差为变量估计最后的平均值。即以为随机变量，、、、，最后的结果是，让：

、。

假设现在样本方差不是除以n-1,而是除以n,顺着这个思路我们看看：

 

 我们看到标星号的最后公式，它和总体方差存在着误差，既然存在着误差，我们就让样本方差乘以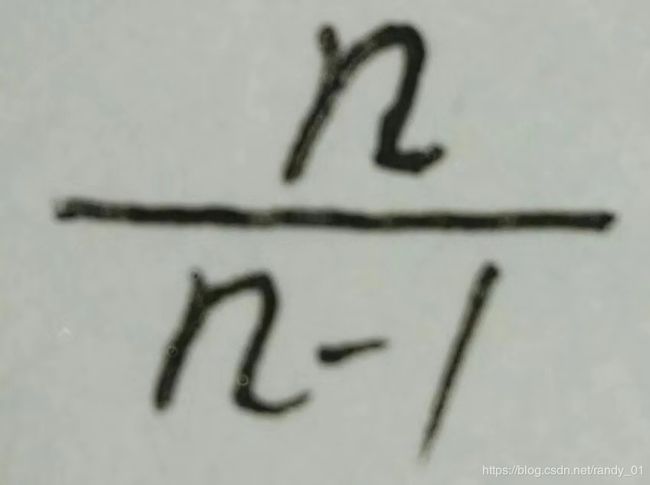，这样我会发现样本方差前的系数就是n-1的倒数了，然后我们再以这个方差为随机变量求最后的方差E(s^2)，结果正好是总体方差。证毕。

1.22 统计泛函

在《实变函数与泛函书分析分析》中已经有明确定义，泛函数的输入是函数空间，输出是实数域，其几何意义是与共轭空间元素的内积，也就是投影。把函数看成是空间中的点或者无限维度的向量，泛函数的几何本质是一个超平面，把输入的函数空间所在的零空间平移输出的实数域个距离。统计泛函是以CDF为输入，在统计学中，均值，方差等指标都是经验估计的，然后用理论证明。经验估计是统计学的基本手段，比如经验分布函数：

比如常见的方差公式是根据经验估计得到的：

至于样本方差的1/（n-1），当n非常大时差别并不大。

1.23 协方差与皮尔逊相关系数

 

 协方差与皮尔逊相关系数的关联：

可以理解为衡量两个变量在变化过程中(以均值为参照点)的平均同步程度，如果为正，说明变化方向一致，如果为负，说明变化方向相反。而大小反应了变化程度，是一个标量，合起来既有方向又有大小。

 这个公式可以用上述描述来理解。协方差只是反映了平均同步的幅度，光靠这个指标不能判断两个独立变量间的相关性。两个变量是否具有相关性应该去除幅度的影响，比如有A,B,C三个变量，cov(A,B)和cov(A,C)都是正值，但是如果两者相差很大，根本看不出相关性，即是否呈线性相关。这个时候如果去除幅度的影响，我们得到一个比值,很明显这个比值比平均幅度更直观，更合理。这个参数就是皮尔逊相关系数。

1.3 不等式

1.31 概率不等式

 

 

 1.32 期望不等式

这部分的不等式对于精通EM算法的人来说非常熟悉。

 

 二、随机变量的收敛

弱大数定律和中心极限定理是这部分的核心内容。