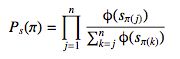原创：机器学习排序深入解读

原创：机器学习排序深入解读

上一篇文章主要介绍了查询与文档内容相似性的打分以及基于概率模型的BM25模型和如何修改lucene的排序源代码。这篇文章将重点讲述机器学习排序，其中的重头戏是关于ListNet算法的英文原版学术论文的解读以及RankLib源码包的学习。

                     机器学习排序:从 Pairwise方法到Listwise方法

Zhe Cao*                                                                                                              

Tao Qin*

清华大学，北京，10084，中国

Tie-Yan Liu

微软亚洲研究院，海淀区知春路49号，10080，中国北京

Ming-Feng Tsai*

国立台湾大学，中华台北 106

Hang Li

微软亚洲研究院，海淀区知春路49号，10080，中国北京

翻译：XueQiang  Tong   http://www.cnblogs.com/txq157   [email protected]

说明：在翻译过程中，我会尽量尊重原著，力求做到简洁易懂，后面会加入自己的一些理解。

摘要

本文主要阐述对排序对象构建机器学习模型(评分函数)。机器学习排序在文档检索、协同过滤以及其他许多领域都有广泛且重要的应用。目前一种基于把”文档对”作为排序对象的机器学习排序方法已经被提出来，在学术界我们把它称为Pairwise方法。尽管Pairwise有所改进，然而它忽略了一个非常重要的事实：我们的排序预测任务是基于所有的排序对象，这些对象的排列顺序要远远多于两个对象的排列。本文论述的机器学习排序方法，是把对象列表(检索出的全部文档)作为排序对象，并且为这个方法提出了一种概率模型。具体来说，我们引入了两个概率模型作为Listwise方法的损失函数，分别是全排列概率模型和top-one概率模型。我们会使用神经网络构建评分函数和梯度下降作为损失函数的优化手段。在信息检索中的经验显示，Listwise比Pairwise表现得更加出色。

1.引言

很多应用的核心事务都离不开排序，比如全文检索，协同过滤，专家搜索，反网络垃圾邮件，情感分析，产品评级等等。不失一般性，本文主要以文档检索为例讨论机器学习排序。当应用于全文检索时，机器学习排序按照如下方式工作：假设现在有一些文档集合，在检索的时候，给定一个查询，然后评分函数给每一个返回的文档打分，按降序排列。每个文档的得分代表了与这个查询的相对相关程度。在机器学习排序的训练中，往往先提供多个查询，其中每个查询都和由这个查询得到的评分文档集合相关联，得到文档后用这些训练数据创建出评分函数，用以精确地预测文档集的得分。

由于它的重要性，近年来机器学习排序在机器学习社区中引起了广泛的关注。在业内被称之为Pairwise的若干方法已经成功用于全文检索。这个方法把一对儿有排列顺序的文档作为训练学习的实例，并且用分类算法来处理。特别地，在训练中，在我们收集到所有文档对儿的全排列之后，对每个文档对儿标识一个代表这两个文档相关程度的标签(-1 or 1)，然后我们用这些数据训练出分类模型，再用这个分类模型排序。SVM、Boosting还有神经网络这些分类模型的应用直接导致RankingSVM(Herbrich et al.,1999)，RankBoost(Freund et al.,1998)，RankNet(Burges et al.,2005)算法的产生。

使用Pairwise方法有很多优势。首先，在分类算法中很多成型的方法可以直接应用于排序中。其次，在特定情况下可以非常容易地获取到文档对儿(Joachims,2002)。

然而，这个方法存在很多缺点。首先，作为训练对象的文档对儿，他所训练出来

的模型的最小化损失函数，是用在分类中而非排序中。其次，文档对儿数量庞大导致计算复杂度太高。第三，文档对儿属于独立同分布(iid)的假设过于(严格)strong，与实际情况相差甚远。最后，不同的查询产生的文档对儿数量变化太大，换句话说文档对儿的数量对查询比较敏感，由于这个差异，将直接导致训练模型更加偏向于拥有更多文档对儿的查询(拥有多数量文档对儿的查询对建模贡献更大)。

在本文中，我们提出Listwise的方法，在这个方法中，我们把文档集作为训练对象。接下来的主要问题是如何定义Listwise的损失函数。我们提出一个概率模型用于listwise损失函数的参数估计。我们会同时把排序函数对文档的打分(此时参数是未知的)和人工对文档显示的或者隐士的打分变换成概率分布，这样我们就可以把两者(特指概率分布)间的距离(差异)作为损失函数。

我们定义了两个概率模型，分别是组合(全排列)概率模型和top one概率。ListNet算法是这样一种算法，它使用listwise的损失函数，优化损失函数前先构建神经网络模型，然后用梯度下降估计参数。事实表明，ListNet算法明显好于Ranking SVM, RankBoost还有 RankNet。

本文主要包括以下4部分：①listwise算法的概述；②基于概率模型的损失函数的转换；③listwise算法的发展；④关于这个算法的实验验证。

2.Related Work

2.1机器学习排序

RankNet算法在对损失函数进行参数估计时，使用交叉熵作为参数搜索方向(构建损失函数)使用梯度下降法优化损失函数，在这个过程中会构建线性神经网络作为评分函数。Pairwise算法被先后应用于信息检索。比如，Joachims(2002)把RankingSVM算法应用于全文检索，他从用户的点击数据(一般从点击图中获取)中获取训练时要用到的文档对儿。

2.2排序中的概率模型

Luce 定义了概率分布模型，他进一步引入参数来表征概率分布并且发明了估计参数的方法。Plackett在投票结果系统上应用了这个模型和方法。本文应用相似的概率分布模型。然而，本文提到的底层结构(parameters)和基本用法(文档分数转换为概率分布) 与Plackett的会有些差异。

3.Listwise方法

这部分，我们将会以全文检索为例，给出关于机器学习排序的一般性的描述，并且在细节上加以详细说明。在以下描述中，我们使用上标表示查询的索引，使用下标表示文档的索引。

在训练中，通常给定这样一组查询Q={q⁽¹⁾,q⁽²⁾,…q^(m)}。每个查询都和文档集合d⁽ⁱ⁾=(d⁽ⁱ⁾₁,d⁽ⁱ⁾₂,…d⁽ⁱ⁾_n(i))相关联,其中d⁽ⁱ⁾_j表示第j个文档，n⁽ⁱ⁾表示第i个查询的文档数目(d⁽ⁱ⁾)。此外，每一组文档d⁽ⁱ⁾都和文档的人工打分y⁽ⁱ⁾=(y⁽ⁱ⁾₁,y⁽ⁱ⁾₂,…y⁽ⁱ⁾n⁽ⁱ⁾)相关联。y⁽ⁱ⁾代表了文档和查询的相关程度，这个分数是人为指定的。比如，这个分数可以由文档d⁽ⁱ⁾_j的点击率转化而来(Joachims, 2002)。这种假设认为具有较高点击率的文档和查询的相关性更强。

一个特征向量 x⁽ⁱ⁾_j = Ψ(q⁽ⁱ⁾, d⁽ⁱ⁾_j) 是由每个查询-文档(q⁽ⁱ⁾, d⁽ⁱ⁾_j)创建而来，i = 1, 2, · · · m，j =1,2, · · · n⁽ⁱ⁾。每个特征向量构成x⁽ⁱ⁾ = (x⁽ⁱ⁾₁,x⁽ⁱ⁾₂,…x⁽ⁱ⁾_n(i))，这是每个查询构成的特征矩阵。对应分数集合y^{(i) =} (y⁽ⁱ⁾₁,y⁽ⁱ⁾₂,…y⁽ⁱ⁾n⁽ⁱ⁾),最后训练集可以表示成T =｛x⁽ⁱ⁾, y⁽ⁱ⁾｝^m_i=1。

然后我们定义一个评分函数f,对每个特征向量x⁽ⁱ⁾_j 输出一个评分f(x⁽ⁱ⁾_j)，对于特征矩阵我们得到一组评分z(i) = (f(x⁽ⁱ⁾₁),f(x⁽ⁱ⁾₂),…f(x⁽ⁱ⁾_n(i)))。学习的目标是在整个数据集上取得总损失函数最小化。
∑^m_i=1L(y⁽ⁱ⁾,z⁽ⁱ⁾)       --------------------- (1)

L为listwise的损失函数。在训练过中，给定一个查询和相关联的文档集，我们把整个文档集的函数打分和人工打分转换成概率分布然后计算差值，利用梯度下降估计出打分函数的最优参数(优化的过程)，然后用测试集提高泛化能力。相比之下，Pairwise方法训练时在文档集中找出所有的文档对儿排列，如果前一个文档的人工打分高于后一个，就标识为1否则为-1，最后用这些训练数据训练出一个分类模型，比如SVM。比如有三个文档，我们暂且命名为a,b,c，全排列为ab(1),ba(-1),ac(1),ca(-1),cb(1),bc(-1)，括号里为预测后的分类。我们可以从所有分类为1的组合中找出文档排列顺序：acb。Pairwise算法将更多的精力放在寻找全排列的文档对儿以及训练分类模型上，复杂度非常高，Listwise解决了这个问题。

4.概率模型

前面我们提出使用两个概率模型中的任意一个计算损失函数，这两个概率模型分别是组合概率和top one 概率。

4.1.Permutation Probability

我们确定了排序对象集合1,2,…n。其中一种排列为{1,2,…,n}。我们写为π 。其中π(j)表示对象在排列中的位置。文档集合的所有可能的排列为Ωn。以后我们有时会互换排名函数和排名函数给出的分数列表。

我们假设，在使用排序函数的排序列表中进行预测时具有不确定性。换句话说，任何排列都是可能的，但是不同的排列可能有不同的似然函数估计。

我们定义的组合概率，在给定评分函数前提下，应该在组合概率的似然估计上取得比较理想的效果。因此，我们有如下定义：

定理1 假设π是排序列表中其中一种排列，Φ(.)是一个递增并且恒大于零的函数。那么，排列组合的概率为：

于任意的排序列表，在前一个文档得分高于后面一个文档得分的情况下，如果两者交换位置，我们将会得到一个更加低值的概率分布。定理4更加简单，如果一个概率分布是按照文档的分数降序排列的，那么他具有最高值的概率分布，反之如果按照升序排列的话，概率分布的值是最低的。

给定两个scores集合，我们根据他们计算出两个组合概率分布模型，然后把这两个模型之间的差值作为listwise的损失函数。然而，对于容量为n的文档集合来说，组合情况是n!,计算起来比较棘手，所有我们考虑使用top-one概率模型。

4.2 Top One Probability

一个对象的top one概率表示这个对象在所有的文档集中排在最前面的概率。

 

 

 

 

需要注意的是ListNet和RankNet很相似。他们的主要区别在于前者把document list 作为训练和预测的对象，后者把 document pair作为实例。比较有趣的是，当有一组查询，每个查询得到的文档数目为2时，listwise的损失函数变得和pairwise几乎相等。RankNet的时间复杂度为O(m .n²_max)(Burges et al.,2005),m代表查询的数目,ｎ代表每个查询对应的最大文档数目。ListNet的时间复杂度为O(m .n_max)。

 

6.实验

我们将使用三个数据集分别与RankNet(Burges et al.,2005)、Ranking SVM (Herbrich et al., 1999)和 RankBoost (Freund et al., 1998)进行精度对比。这里的ListNet使用top one概率模型。

为了简单起见，在本次实验中，我们使用线性神经网络模型并且省略常量b:

，尖括号里面代表向量内积。

6.1数据集

我们使用3个数据集：TREC，OHSUMED，CSearch。TREC数据集包括了1053110个pages,11164829个超链接，这些数据是查询50次得到的。在构造特征向量时，考虑了内容特征和超链接特征，总共有20个。OHSUMED数据集包括了348556个documents，106个queries，16140个文档对儿，总共构建了30个特征。CSearch大约包含了25000 queries，每个query有1000多个关联文档，构建了600个features，包括query dependent features and independent features.这个数据集提供了5个等级的评分：4 (”perfect match”) to 0 (”bad match”)。

为了使排序更加接近真实情况，我们创建训练数据集的时候将使用”评分等级”来表示关联程度的高低(离散关联判断)。在排名性能评估上，我们采用两个常用的IR评价措：NDCG和MAP。NDCG is designed to measure ranking accuracy when there are more than two levels of relevance　judgments. For MAP it is assumed that there are two levels: relevant and irrelevant.关于这两部分的理解，可以参看http://www.cnblogs.com/HappyAngel/p/3535919.html。NDCG主要用于评分等级大于2个的场景，而MAP主要用于评分等级为相关和不相关的场景。

6.2排序精度

对于TREC和OHSUMED我们把每个数据集分成5个部分,实施”五折交叉验证”。 在每次实验中，3/5用于训练，1/5用于验证，剩下的1/5用于测试。对于RankNet和ListNet算法，在每次实验中验证集主要用于确定最优化的迭代次数以便训练出最优的模型。对于RankingSVM算法主要是调整系数C而RankBoost算法主要寻找出最佳的weak learns的数量。在第6部分我们输出的报告(精度)为五次实验的平均值。

Figure 1和Table 1给出了TREC 的报告结果。结果显示，ListNet算法的表现要优于其他三种方法。尤其在Table1的报告中，我们看到在第一次和第二次试验中ListNet的NDCG值超越RankNet大约4个point gain，带来大约10%的搜索结果相关性的改进。

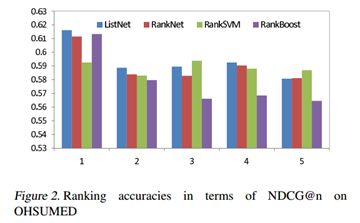
Figure 2和Table 2显示了OHSUMED数据集的试验结果。再一次，在所有的评估中，ListNet仍然优于RankNet和RankBoost。此外，除了第3次和第5次试验外，ListNet算法均优于RankSVM(用NDCG评估)。

CSearch的数据量非常庞大，我们没有采用交叉验证的方式。我们从中随机选取1/3作为训练，1/3用于验证，剩下的1/3用于测试。Figure3显示了ListNet，RankNet和RankBoost的试验结果。ListNet算法再一次不负众望。由于数据量的原因，我们不能实施RankingSVM。

 

 

 

 

6.3讨论

我们来讨论一下为什么基于listwise的方法ListNet优于基于pairwise的方法RankNet,RankingSVM还有RankBoost。就像在第一部分解释过的那样，在pairwise方法中文档对儿的数量受查询影响很大，结果导致在训练时训练模型更加偏向于拥有较多文档对儿的查询。并且我们在几乎所有的测试数据集中都观察到这种倾向。Table 2显示了在OHSUMED数据集上每一个查询的文档对儿的分布情况。

我们看到分布呈现明显的倾斜：更多的查询只拥有很少的文档对儿，只有少数的查询拥有较多的文档对儿。在listwise方法中损失函数在每个查询中都有定义，所以这个问题跟本不存在。(由于listwise把整个文档集作为训练对象，不会出现训练模型的倾向问题) This appears to be one of the reasons for the higher performance(高性能) by ListNet。

第二个问题就是pairwise的损失函数问题。由于pairwise实际上把排序问题转换成了分类问题，使用分类算法的损失函数对于排序来说，它所付出的代价可能会更大。而且对于MAP和NDCG这样的评估准则，更加适合用在把整个文档集作为训练集的场景，pairwise的损失函数对于上述的评估准则来说会显得更加松散。

我们更进一步分析两者的损失函数的不同点。这一次我们使用TREC数据集的Figure4和Figure5来说明。可以看到，在训练中，pairwise的损失函数并不是完全和NDCG成反比(理想状态应该是呈现反比关系，即损失函数越小，NDCG越大)。从数据中我们看到，从第20次迭代到第50次迭代过程中，两者(loss function and NDCG)还是呈现反比关系的。然而60次以后，尽管pairwise的损失函数在下降，NDCG值却并没有上升。相比之下，listwise的损失函数完全和NDCG呈现反比关系。另外，从图中明显看出，pairwise损失函数收敛的速度也明显慢于listwise。

最终我们得出结论，listwise方法的性能明显优于pairwise，更适合于机器学习排序。

 

 

7.结论

在本文中，我们提出了一种新的学习方法排名，称为listwise方法。我们认为
在学习排名时采用这种方法比传统的成对法更好。在listwise方法中，不是使用对象对作为实例，我们使用对象列表作为学习中的实例。Listwise方法的关键问题是定义一个listwise损失函数。在本文中，我们提出采用概率方法来解决它。具体来说，我们使用概率模型：组合概率和top-one概率将文档排名分数转换为概率分布模型。然后，我们可以把两个概率分布模型之间的任何差值度量（例如，交叉熵）视为listwise损失函数。
我们然后开发了一种基于该方法的学习方法，使用线性神经网络构建评分函数,使用交叉熵构建损失函数，使用梯度下降法对损失函数进行优化。使用三个数据集的实验结果表明，该方法比现有的pairwise方法（如RanNet，Ranking SVM和RankBoost）更好，这表明最好采用listwise方法来学习排名。除此之外，我们还调查了pairwise损失函数和性能评估指标（如NDCG和MAP）之间的关系。

8.致谢

 

Bin Gao对这项工作提出了许多有价值的建议。我们还要感谢Kai Yi对我们实验的帮助。

9.参考工具

Baeza-Yates, R., & Ribeiro-Neto, B. (1999). Modern information retrieval. Addison Wesley.
Burges, C., Shaked, T., Renshaw, E., Lazier, A., Deeds, M.,Hamilton, N., & Hullender, G. (2005). Learning to rank using gradient descent. Proceedings of ICML 2005 (pp.89–96).
Cao, Y. B., Xu, J., Liu, T. Y., Li, H., Huang, Y. L., & Hon, H. W. (2006). Adapting ranking SVM to document retrieval. Proceedings of SIGIR 2006 (pp. 186–193).

Cohen, W. W., Schapire, R. E., & Singer, Y. (1998). Learning to order things. Advances in Neural Information Processing Systems. The MIT Press.
Crammer, K., & Singer, Y. (2001). Pranking with ranking.Proceedings of NIPS 2001.
Craswell, N., Hawking, D., Wilkinson, R., & Wu, M.(2003). Overview of the TREC 2003 web track. Proceedings of TREC 2003 (pp. 78–92).
Freund, Y., Iyer, R., Schapire, R. E., & Singer, Y. (1998).
An efficient boosting algorithm for combining preferences. Proceedings of ICML 1998 (pp. 170–178).
Herbrich, R., Graepel, T., & Obermayer, K. (1999). Support vector learning for ordinal regression. Proceedings of ICANN 1999 (pp. 97–102).
Hersh, W. R., Buckley, C., Leone, T. J., & Hickam, D. H.(1994).

OHSUMED: An interactive retrieval evaluation and new large test collection for research. Proceedings of SIGIR 1994 (pp. 192–201).
Jarvelin, K., & Kekanainen, J. (2000). IR evaluation methods for retrieving highly relevant documents. Proceedings of SIGIR 2000 (pp. 41–48).
Joachims, T. (1999). Making large-scale support vector machine learning practical. Advances in kernel methods: support vector learning, 169–184.
Joachims, T. (2002). Optimizing search engines using clickthrough data. Proceedings of KDD 2002 (pp. 133–142).
Lebanon, G., & Lafferty, J. (2002). Cranking: Combining rankings using conditional probability models on permutations. Proceedings of ICML 2002 (pp. 363–370).
Luce, R. D. (1959). Individual choice behavior. Wiley. Matveeva, I., Burges, C., Burkard, T., Laucius, A., & Wong, L. (2006).

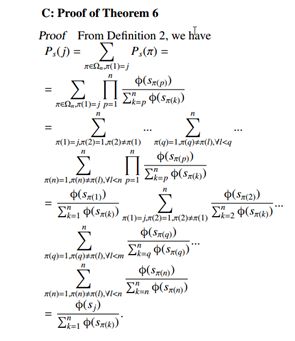
10.附录

A: Proof of Lemma 2

 

 

 

 

End。

posted @ 2017-03-30 18:59 佟学强 阅读( ...) 评论( ...) 编辑 收藏