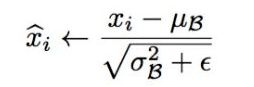Batch Normalization 和 Group Normalization
Batch Normalization
Batch Normalization 在深度学习上算是不可或缺的一部分,基本上所有的框架中都会用到它,我记得比较清楚的是,在YOLOV2中作者采用了Batch Normalization 从而提高了4个百分点的Map吧。
为何要提出Batch Normalization?
本人偏向于computer vision 这一块,在每次给network输入数据时,都需要进行预处理,比如归一化之类的,为什么需要归一化呢?神经网络学习过程本质就是为了学习数据分布,一旦训练数据与测试数据的分布不同,那么网络的泛化能力也大大降低;另外一方面,一旦每批训练数据的分布各不相同(batch 梯度下降),那么网络就要在每次迭代都去学习适应不同的分布,这样将会大大降低网络的训练速度,这也正是为什么我们需要对数据都要做一个归一化预处理的原因。
而且在训练的过程中,经过一层层的网络运算,中间层的学习到的数据分布也是发生着挺大的变化,这就要求我们必须使用一个很小的学习率和对参数很好的初始化,但是这么做会让训练过程变得慢而且复杂m在论文中,这种现象被称为Internal Covariate Shift。为了解决这个问题,作者提出了Batch Normalization。
Batch Normalization原理
为了降低Internal Covariate Shift带来的影响,其实只要进行归一化就可以的。比如,我们把network每一层的输出都整为方差为1,均值为0的正态分布,这样看起来是可以解决问题,但是想想,network好不容易学习到的数据特征,被你这样一弄又回到了解放前了,相当于没有学习了。所以这样是不行的,大神想到了一个大招:变换重构,引入了两个可以学习的参数γ、β,当然,这也是算法的灵魂所在:
具体的算法流程如下:
Batch Normalization 是对一个batch来进行normalization的,例如我们的输入的一个batch为:β=x_(1...m),输出为:y_i=BN(x)。具体的完整流程如下:
1.求出该batch数据x的均值
2.求出该batch数据的方差
3.对输入数据x做归一化处理,得到:
4.最后加入可训练的两个参数:缩放变量γ和平移变量β,计算归一化后的值:
加入了这两个参数之后,网络就可以更加容易的学习到更多的东西了。先想想极端的情况,当缩放变量γ和平移变量β分别等于batch数据的方差和均值时,最后得到的yi就和原来的xi一模一样了,相当于batch normalization没有起作用了。这样就保证了每一次数据经过归一化后还保留的有学习来的特征,同时又能完成归一化这个操作,加速训练。
引入参数的更新过程,也就是链式法则:
一个简单例子:
def Batchnorm_simple_for_train(x, gamma,beta, bn_param):"""
param:x : 输入数据,设shape(B,L)
param:gama : 缩放因子 γ
param:beta : 平移因子 β
param:bn_param : batchnorm所需要的一些参数
eps : 接近0的数,防止分母出现0
momentum : 动量参数,一般为0.9,0.99, 0.999
running_mean :滑动平均的方式计算新的均值,训练时计算,为测试数据做准备
running_var : 滑动平均的方式计算新的方差,训练时计算,为测试数据做准备
"""
running_mean = bn_param['running_mean'] #shape = [B]
running_var = bn_param['running_var'] #shape = [B]
results = 0. # 建立一个新的变量
x_mean=x.mean(axis=0) # 计算x的均值
x_var=x.var(axis=0) # 计算方差
x_normalized=(x-x_mean)/np.sqrt(x_var+eps) # 归一化
results = gamma * x_normalized + beta # 缩放平移
running_mean = momentum * running_mean + (1 - momentum) * x_mean
running_var = momentum * running_var + (1 - momentum) * x_var #记录新的值
bn_param['running_mean'] = running_mean
bn_param['running_var'] = running_var
return results , bn_param看完这个代码是不是对batchnorm有了一个清晰的理解,首先计算均值和方差,然后归一化,然后缩放和平移,完事!但是这是在训练中完成的任务,每次训练给一个批量,然后计算批量的均值方差,但是在测试的时候可不是这样,测试的时候每次只输入一张图片,这怎么计算批量的均值和方差,于是,就有了代码中下面两行,在训练的时候实现计算好mean var测试的时候直接拿来用就可以了,不用计算均值和方差。
running_mean = momentum * running_mean + (1- momentum) * x_mean
running_var = momentum * running_var + (1 -momentum) * x_var所以,测试的时候是这样的:
def Batchnorm_simple_for_test(x, gamma,beta, bn_param):"""
param:x : 输入数据,设shape(B,L)
param:gama : 缩放因子 γ
param:beta : 平移因子 β
param:bn_param : batchnorm所需要的一些参数
eps : 接近0的数,防止分母出现0
momentum : 动量参数,一般为0.9,0.99, 0.999
running_mean :滑动平均的方式计算新的均值,训练时计算,为测试数据做准备
running_var : 滑动平均的方式计算新的方差,训练时计算,为测试数据做准备
"""
running_mean = bn_param['running_mean'] #shape = [B]
running_var = bn_param['running_var'] #shape = [B]
results = 0. # 建立一个新的变量
x_normalized=(x-running_mean )/np.sqrt(running_var +eps) # 归一化
results = gamma * x_normalized + beta # 缩放平移
return results , bn_param整个过程还是很顺的,很好理解的。这部分的内容摘抄自微信公众号:机器学习算法工程师。一个很好的公众号,推荐一波。
Batch Normalization 的TensorFlow 源码解读,来自知乎:
def batch_norm_layer(x, train_phase,scope_bn):
with tf.variable_scope(scope_bn):
# 新建两个变量,平移、缩放因子
beta = tf.Variable(tf.constant(0.0, shape=[x.shape[-1]]), name='beta',trainable=True)
gamma = tf.Variable(tf.constant(1.0, shape=[x.shape[-1]]), name='gamma',trainable=True)
# 计算此次批量的均值和方差
axises = np.arange(len(x.shape) - 1)
batch_mean, batch_var = tf.nn.moments(x, axises, name='moments')
# 滑动平均做衰减
ema = tf.train.ExponentialMovingAverage(decay=0.5)
def mean_var_with_update():
ema_apply_op = ema.apply([batch_mean, batch_var])
with tf.control_dependencies([ema_apply_op]):
return tf.identity(batch_mean),tf.identity(batch_var)
# train_phase 训练还是测试的flag
# 训练阶段计算runing_mean和runing_var,使用mean_var_with_update()函数
# 测试的时候直接把之前计算的拿去用 ema.average(batch_mean)
mean, var = tf.cond(train_phase, mean_var_with_update,
lambda:(ema.average(batch_mean), ema.average(batch_var)))
normed = tf.nn.batch_normalization(x, mean, var, beta, gamma, 1e-3)
return normed至于此行代码tf.nn.batch_normalization()就是简单的计算batchnorm过程,这个函数所实现的功能就如此公式:
def batch_normalization(x, mean, variance, offset,scale, variance_epsilon, name=None):
with ops.name_scope(name, "batchnorm", [x, mean, variance,scale, offset]):
inv = math_ops.rsqrt(variance + variance_epsilon)
if scale is not None:
inv *= scale
return x * inv + (offset - mean * inv
if offset is not Noneelse -mean * inv)Batch Normalization的带来的优势:
没有它之前,需要小心的调整学习率和权重初始化,但是有了BN可以放心的使用大学习率,但是使用了BN,就不用小心的调参了,较大的学习率极大的提高了学习速度,
Batchnorm本身上也是一种正则的方式,可以代替其他正则方式如dropout等
另外,个人认为,batchnorm降低了数据之间的绝对差异,有一个去相关的性质,更多的考虑相对差异性,因此在分类任务上具有更好的效果
Group Normalization
group normalization是2018年3月份何恺明大神的又一力作,优化了batch normalization在比较小的batch size 情况下表现不太好的劣势。批量维度进行归一化会带来一些问题——批量统计估算不准确导致批量变小时,BN 的误差会迅速增加。在训练大型网络和将特征转移到计算机视觉任务中(包括检测、分割和视频),内存消耗限制了只能使用小批量的BN。尤其是在我的破电脑里面,batch的大小一般都是使用的1,相当于不存在BN。
以后是论文中给出BN和GN的对比:
可以看出在bath size比较小的情况下,BN的性能十分地差,而GN的性能基本上没有太大改变。我明天也打算把mask r-cnn中的BN都换成GN试试,看看效果会不会有所提高。
Group Normalization 原理:
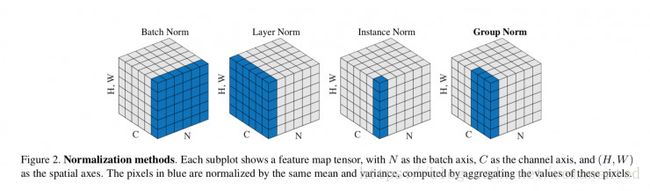
先给出他目前出现比较多的几种normalization的示意图:
BatchNorm:batch方向做归一化,算N*H*W的均值
LayerNorm:channel方向做归一化,算C*H*W的均值
InstanceNorm:一个channel内做归一化,算H*W的均值
GroupNorm:将channel方向分group,然后每个group内做归一化,算(C//G)*H*W的均值
从示意图中看,也可以看出其实没有太大的变化,所以代码中也没有需要太大的变动,只需要稍微修改一下就好了。
GN代码实现:
def GroupNorm(x,G=16,eps=1e-5):
N,H,W,C=x.shape
x=tf.reshape(x,[tf.cast(N,tf.int32),tf.cast(H,tf.int32),tf.cast(W,tf.int32),tf.cast(G,tf.int32),tf.cast(C//G,tf.int32)])
mean,var=tf.nn.moments(x,[1,2,4],keep_dims=True)
x=(x-mean)/tf.sqrt(var+eps)
x=tf.reshape(x,[tf.cast(N,tf.int32),tf.cast(H,tf.int32),tf.cast(W,tf.int32),tf.cast(C,tf.int32)])
gamma = tf.Variable(tf.ones(shape=[1,1,1,tf.cast(C,tf.int32)]), name="gamma")
beta = tf.Variable(tf.zeros(shape=[1,1,1,tf.cast(C,tf.int32)]), name="beta")
return x*gamma+beta 添加:作为一个keras的忠实用户,当然还是得把keras版本实现贴出来的,其实也是在keras中的BatchNormalization层上进行一定的修改就得到了GroupNormalization层。
正常和batchnormalization一样的调用即可。但注意需要保持channel数是group的整数倍。