搜索算法详解
- 前言
- 纲要
- DFS 深度优先搜索算法
- 定义
- 基本内容
- 主要思想
- 操作方法
- 典型的题
- 地图可达性问题
- 地图片区问题
- 普通的DFS模型
- BFS 广度优先搜索算法
- 定义
- 基本内容
- 主要思想
- 操作方式
- 典型的题
- 地图可达性问题
- 地图的最短路问题
- 地图片区问题
- 剪枝
- 定义
- 基本内容
- 典型的题
- 记忆化搜索
- 定义
- 基本内容
- 主要思想
- 操作方法
- 典型的题
前言
什么。。。我一个挂掉省选的人居然还要祸害下一届的萌萌哒学生。。。心痛啊。。。
教练居然要我讲搜索算法。。。然而里面居然有我不会的东西。。。法克啊。。。
这个博客存在的意义就是。。。边讲边学。。。等到我会了。。。这个东西也就完备了(然而我看这个坑是填不完的)。。。
纲要
主要讲这些东西:
- DFS 深度优先搜索算法
- BFS 广度优先搜索算法
- 剪枝
- 记忆化搜索
- 迭代加深算法
- 启发式搜索算法
- 启发式迭代加深,IDA*算法
- A*算法
那我们来一个一个的看吧。
DFS 深度优先搜索算法
定义
这玩意还需要定义???好吧好吧。。。
事实上,深度优先搜索属于图算法的一种,英文缩写为DFS即Depth First Search.其过程简要来说是对每一个可能的分支路径深入到不能再深入为止,而且每个节点只能访问一次。(选自百度百科)
别的我也写不粗来啦。。。QWQ
基本内容
主要思想
在搜索过程中,我们定义一个深度的定义方式,以作为搜索的参考依据。
在一般的图论DFS中,深度的定义即为:当前搜索到的路径长度。
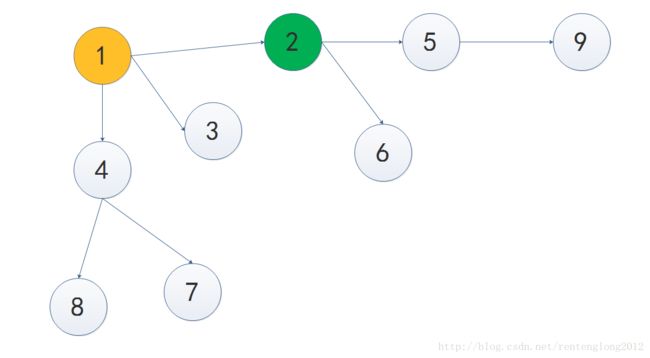
例如说在这张图里面:
黄色圈代表起点
蓝色圈代表终点
绿色圈代表目前已经搜索到的东西。。。
红色线代表了当前搜索到的道路。。。
现在已经搜索到了8号点,深度是5。
还有其他的例子。在下面的例题里面讲解。
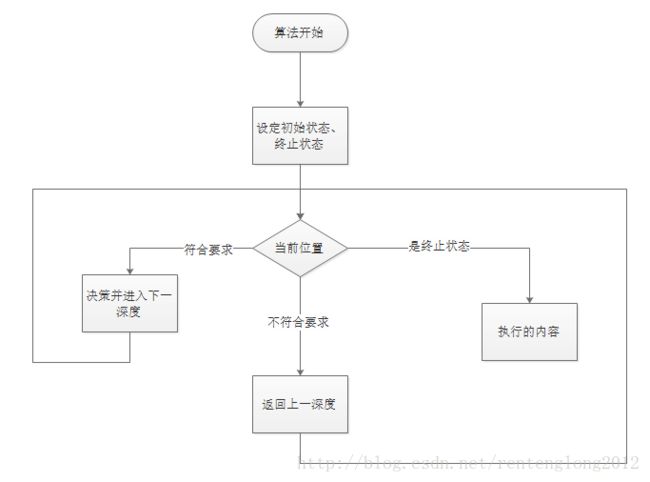
操作方法
关于“是终止状态”的执行内容:
- 可以是结束整个程序
- 可以是返回上一层并继续执行其他的深度,直到无法继续进行
- 亦或者是达到某一个特殊的条件等等,比较灵活。
但是注意,终止条件是必不可少的,如果没有,则必定造成死循环。
典型的题
地图可达性问题
OpenJudge 1818:红与黑
总时间限制: 1000ms
内存限制: 65536kB
描述
有一间长方形的房子,地上铺了红色、黑色两种颜色的正方形瓷砖。你站在其中一块黑色的瓷砖上,只能向相邻的黑色瓷砖移动。请写一个程序,计算你总共能够到达多少块黑色的瓷砖。
输入
包括多个数据集合。每个数据集合的第一行是两个整数W和H,分别表示x方向和y方向瓷砖的数量。W和H都不超过20。在接下来的H行中,每行包括W个字符。每个字符表示一块瓷砖的颜色,规则如下
1)‘.’:黑色的瓷砖;
2)‘#’:白色的瓷砖;
3)‘@’:黑色的瓷砖,并且你站在这块瓷砖上。该字符在每个数据集合中唯一出现一次。
当在一行中读入的是两个零时,表示输入结束。
输出
对每个数据集合,分别输出一行,显示你从初始位置出发能到达的瓷砖数(记数时包括初始位置的瓷砖)。
样例输入
6 9
....#.
.....#
......
......
......
......
......
#@...#
.#..#.
0 0
样例输出
45
这个题嘛。。。灰常简单啦。。。
简单分析一下:
- 初始状态就是给定的初始位置
- 决策方式是“目标位置是否被访问过”以及“目标位置能否被访问”
- 每到一个新的状态以后,将该状态标记为“已访问”
- 终止状态是第1层的决策无法进行。
来吧,看标程(程序已经老了。。。很久很久以前的了。。。马蜂跟现在不一样)。
#include1; //初始化
for(int i=1;i<=m;i++)
{
for(int j=1;j<=n;j++) map[i][j]=false;//初始化
}
}
return 0;
} 地图片区问题
OpenJudge 1817:城堡问题
描述
1 2 3 4 5 6 7
#############################
1 # | # | # | | #
#####---#####---#---#####---#
2 # # | # # # # #
#---#####---#####---#####---#
3 # | | # # # # #
#---#########---#####---#---#
4 # # | | | | # #
#############################
(图 1)
# = Wall
| = No wall
- = No wall
图1是一个城堡的地形图。请你编写一个程序,计算城堡一共有多少房间,最大的房间有多大。城堡被分割成m*n(m≤50,n≤50)个方块,每个方块可以有0~4面墙。
输入
程序从标准输入设备读入数据。第一行是两个整数,分别是南北向、东西向的方块数。在接下来的输入行里,每个方块用一个数字(0≤p≤50)描述。用一个数字表示方块周围的墙,1表示西墙,2表示北墙,4表示东墙,8表示南墙。每个方块用代表其周围墙的数字之和表示。城堡的内墙被计算两次,方块(1,1)的南墙同时也是方块(2,1)的北墙。输入的数据保证城堡至少有两个房间。
输出
城堡的房间数、城堡中最大房间所包括的方块数。结果显示在标准输出设备上。
样例输入
4
7
11 6 11 6 3 10 6
7 9 6 13 5 15 5
1 10 12 7 13 7 5
13 11 10 8 10 12 13
样例输出
5
9
这算是DFS的另外一个用途了,专门用来打标记。
思路是这样的:我们将这n*m个格子全都扫描一遍。如果扫描到的格子是未被标记的,那么我们就以这个格子为起点开始DFS,以此给所有这个格子能够访问到的格子打上标记,并统计相连的格子数。
看图,我们来演示一下样例:
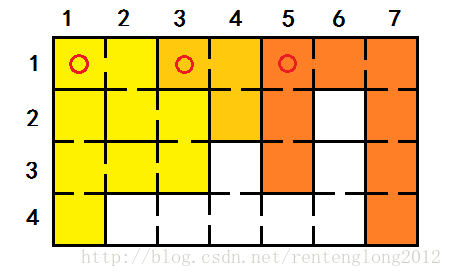
这是样例本来的样子。
进行了扫描,发现第一个格子没有标记(红圈提示的格子):
然后我们对它进行一波操作:
黄色是打上标记的格子,并统计出个数(9)。
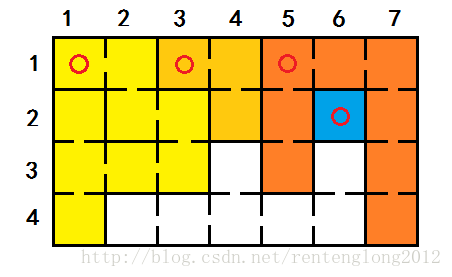
我们继续扫描,又扫描到一个空的:
给它做上标记,并统计出个数(3):
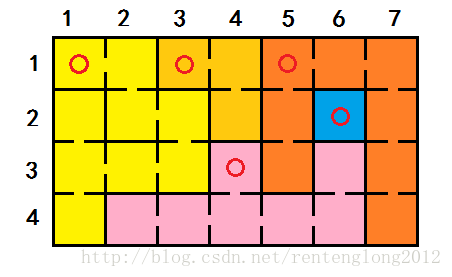
同理,又找到一个,并统计出个数(8):
下一个,并统计出个数(1):
下一个,并统计出个数(7):
然后扫描到最后一个格子,结束,共计5片区域,最大区域有9个格子。
普通的DFS模型
OpenJudge 1756:八皇后
总时间限制: 1000ms
内存限制: 65536kB
描述
会下国际象棋的人都很清楚:皇后可以在横、竖、斜线上不限步数地吃掉其他棋子。如何将8个皇后放在棋盘上(有8 * 8个方格),使它们谁也不能被吃掉!这就是著名的八皇后问题。
对于某个满足要求的8皇后的摆放方法,定义一个皇后串a与之对应,即 a=b1b2...b8 ,其中 bi 为相应摆法中第i行皇后所处的列数。已经知道8皇后问题一共有92组解(即92个不同的皇后串)。
给出一个数b,要求输出第b个串。串的比较是这样的:皇后串x置于皇后串y之前,当且仅当将x视为整数时比y小。
输入
第1行是测试数据的组数n,后面跟着n行输入。每组测试数据占1行,包括一个正整数b(1 <= b <= 92)
输出
输出有n行,每行输出对应一个输入。输出应是一个正整数,是对应于b的皇后串。
样例输入
2
1
92
样例输出
15863724
84136275
比较典型的问题,八皇后问题。
我们可以先把92种情况全部预处理一遍,然后需要哪个输出哪个就行了。
那么:
- 指定当前状态为当前的行数,即深度为行数。
- 状态转移的方式是进入下一层。
- 终止状态是第一行的情况已经全部用完。
看程序:
#includeif(j+ans[j]==now+i||j-ans[j]==now-i)
{
ok=false;
break;
}
}
if(sf[i]==true&&ok==true)
{
sf[i]=false;
ans[now]=i;
dfs(now+1);
sf[i]=true;
}
}
}
int main()
{
dfs(1);
int n,a;
cin>>a;
while(a--)
{
cin>>n;
for(int i=1;i<=8;i++)
{
cout<cout<return 0;
} BFS 广度优先搜索算法
定义
宽度优先搜索算法(又称广度优先搜索)是最简便的图的搜索算法之一,这一算法也是很多重要的图的算法的原型。Dijkstra单源最短路径算法和Prim最小生成树算法都采用了和宽度优先搜索类似的思想。其别名又叫BFS,属于一种盲目搜寻法,目的是系统地展开并检查图中的所有节点,以找寻结果。换句话说,它并不考虑结果的可能位置,彻底地搜索整张图,直到找到结果为止。
没错你没看错这玩意还是百度百科。。。
基本内容
主要思想
相比于DFS,即以深度为优先的搜索算法来看,BFS广度优先搜索算法以其广度作为转移的参考依据。
在访问到相应的深度时,DFS会选择直接进入下一层,并在无法前进时折返,而BFS则会现将本层的所有节点全部访问,然后再进入下一层。
操作方式
然后讲讲怎么进行一波操作。
我们考虑到队列的性质: 先进先出。
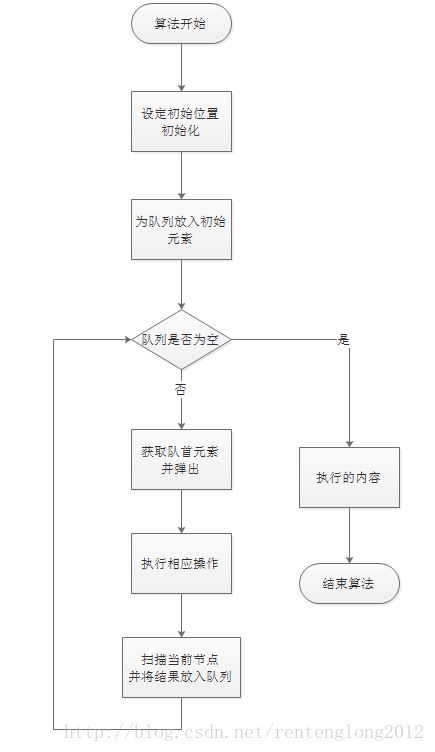
那么我们可以利用这样的性质,在访问到一个节点的时候,我们扫描一遍所有它能到达的节点,并把这些能够到达的节点全部加入到队列的尾部。完毕以后,再从队列里拿取一个节点,并继续扫描这个节点,知道队列变成空的为止。
那画成图就是这个样子:
文字叙述的形式:
- 清空队列
- 为队列增加起点所在节点
- 在队列首部取出一个节点
- 扫描这个节点所能到达的节点,并将它们放在队列尾部(任意顺序)
- 结束本节点的动作,并准备再次拿取队列首部节点,直到队列为空。
然后要注意,许多利用BFS的算法,其实有许多都利用了被访问到的节点的深度。那么这个深度是指什么?
其实就是相对于初始节点的最短距离。
我们可以在队列记录节点的同时来记录当前结点的深度。每次放入队列的新元素的深度就是当前节点的深度+1。
典型的题
地图可达性问题
同样还是跟DFS一样的地图可达性问题。只不过可以使用BFS来做。
例题不再举了,随便想一个都可以。我们领会思路:
就是每次扫描节点过程中,如果扫描到了终点,那么就可以直接结束程序,并表示“可达”。如果队列为空以后还没能接触到终点,那就是“不可达”。
地图的最短路问题
首先,同样是DFS也能做,但是DFS的效率将会非常低,因为DFS必须将所有的路全部枚举,才能比较出最小值。
但是BFS则不同。由于BFS按照广度优先,然后逐层扩散,所以它第一次访问到某个节点所计算出的深度一定是起点到该节点的最短路。
那么,我们如果在扫描过程中扫描到了终点,那么就可以直接结束程序,最短路径长度为被扫描到的节点的深度。如果队列为空以后还没能接触到终点,那就是“不可达”。
OpenJudge 2753:走迷宫
总时间限制: 1000ms
内存限制: 65536kB
描述
一个迷宫由R行C列格子组成,有的格子里有障碍物,不能走;有的格子是空地,可以走。
给定一个迷宫,求从左上角走到右下角最少需要走多少步(数据保证一定能走到)。只能在水平方向或垂直方向走,不能斜着走。
输入
第一行是两个整数,R和C,代表迷宫的长和宽。( 1<= R,C <= 40)
接下来是R行,每行C个字符,代表整个迷宫。
空地格子用’.’表示,有障碍物的格子用’#’表示。
迷宫左上角和右下角都是’.’。
输出
输出从左上角走到右下角至少要经过多少步(即至少要经过多少个空地格子)。计算步数要包括起点和终点。
样例输入
5 5
..###
#....
#.#.#
#.#.#
#.#..
样例输出
9
就像刚才所说的就行啦。。。
#includereturn 0;
} 地图片区问题
和DFS一样的,只要将填充区块的方式改成BFS就可以了。
剪枝
定义
这东西没有定义啦。。。
在进行搜索算法的过程中,将已知无法继续进行的情况排除的行为叫做剪枝。
基本内容
也就是说,我们假设:
现在扫描已经进行到第2号节点,但是2号节点是一个不符合要求的节点。那么如果我们可以直接确定它后面的5、6、9号节点都不符合要求的话,那么我们直接跳过它们就行了。这样能够极大地提升效率。
典型的题
这玩意怎么会有典型的题。。。这可是具体问题具体分析的题啊。。。
但是我可以出一个有代表性的。
找路
总时间限制: 1000ms
内存限制: 65536kB
描述
给你1张n*m地图,给你初始位置和末位置,空地格子用’.’表示,有障碍物的格子用’#’表示,起点’S’,终点’T’,问在k步内能否抵达终点(即最短路距离小于等于k)。
输入
第一行,3个整数n、k,中间一个空格隔开。
接下来n行,每行m个字符代表了地图。
输出
一个字符,Y代表能,N代表不能。
样例输入1
5 5 4
..###
#.S..
#.#.#
#.#.#
#.#T.
样例输出1
Y
样例输入2
5 5 2
..###
#.S..
#.#.#
#.#.#
#.#T.
样例输出2
N
然后这个题完全可以直接用BFS先求出最短路,然后进行比对。但是这样做会造成很大的浪费。我们可以对它的搜索过程进行剪枝,如果深度超过了k,就直接跳过对该节点的入队和扫描。
程序:
#includereturn 0;
} 记忆化搜索
定义
这好像还是没有定义。
对于一个搜索状态,如果这个状态的结果是确定的,那么将本次搜索状态记录下来并在下次使用此状态时直接返回记录结果的行为叫做记忆化搜索。
基本内容
主要思想
主要是在“记忆”上。
记忆化搜索主要是使用数组或其他形式来记录某一搜索状态的结果,这样在下一次重复使用该搜索结果的时候,可以以较低的复杂度(一般来讲是 O(1) ,也可以是 O(log) ,取决于记忆化的实现方式)来获取相同的结果。
所以在进行搜索算法的时候,要想实现记忆化,就必须尽可能地优化搜索的方式,并尽可能压缩确定一个搜索状态所需要的参数。
由于DFS在进行搜索的过程中,会优先向最深处前进,因此更容易配合记忆化搜索。BFS。。。也许可以呢,但是我没见过。
操作方法
主要有这样的操作:
- 建立对应的存储方式
- 计算并存储一个状态
- 读取一个状态
然后就没啦。。。在C++一般比较喜欢使用数组(或者map)来实现。
典型的题
这个。。。其实也是具体问题具体分析的。。。没有典型的题可说。。。
但是还是找一个最简单的例子来说明好了。
斐波那契数列
总时间限制: 1000ms
内存限制: 65536kB
描述
已知斐波那契数列的定义:
fib(1)=fib(2)=1
fib(n)=fib(n−1)+fib(n−2),n>2
那么你来算斐波那契的第x项,即 fib(x) 。
输入
一行,一个整数x,x<1000000
输出
一个整数,代表 fib(x) 。
样例输入
6
样例输出
8
然而这种问题,首先。。。直接用一个循环到x不行吗。。。当然行,但是为了练习记忆化,建议你先用递归。。。
首先来讲我们写一个递归。
#includereturn 0;
} 但是你很容易发现,这样的程序,x稍微一大就不行了,直接TLE。
为啥?看图:
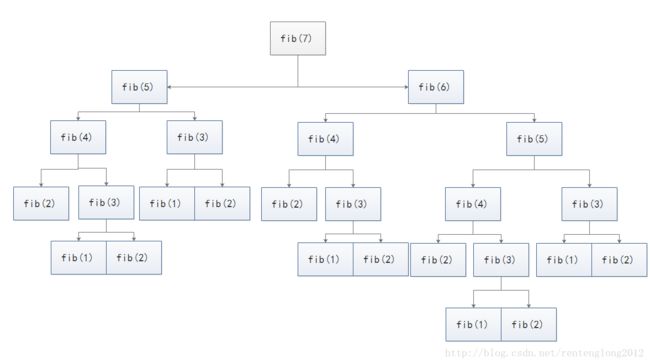
这个图代表要计算fib(7),首先要计算fib(5)和fib(6)。
那么完整分析一下fib(7):
你会发现:似乎计算fib(7)直接使用递归,计算的次数非常多。而且事实上,如果我把相同的计算(因为fib(x)的值,即斐波那契数列的第x项是确定的,因此重复计算是多余的)用颜色标注出来:
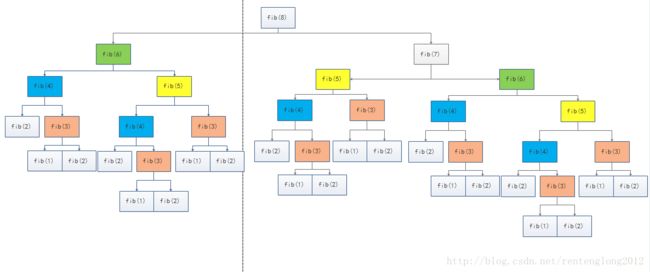
你会发现,最坏的fib(3)被重复计算了5次。虽然在fib(7)这样的计算里,重复这几次没有什么。但是当x一旦变大,这将会是指数级别的爆炸。
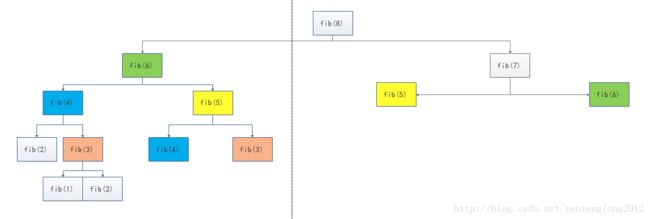
看,在计算fib(8)的时候,明显的计算次数增加了很多。
那么我们可以通过一个数组来记录已经计算完毕的内容。然后计算次数就会减少很多(下图将按照从左向右、从上到下的顺序计算):
在这张图里,调用结果被算作是 O(1) 的复杂度。
通过上面的图,你会发现:计算次数真的少了很多,效率也会因此得到非常大的提升。
#includereturn 0;
} 而且程序改动幅度很小。基本上就是一个定义、一个判断、一个访问和一个修改。