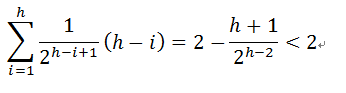题目:http://www.lydsy.com/JudgeOnline/problem.php?id=3217
这题一看就是treap或替罪羊树套trie,然后我就很愉快的码了300+treap代码,然后光荣TLE,然后继续常数优化,愉快的刷了一版的TLE后找@lz1 大神要了份神代码对着改了半天,最后发现指针版的居然要比数组模拟快上一半左右(再也不相信数组了...QaQ),然后这才总算A掉了...(然后就居然rank2了额。。。)
吃饱了没事做,顺便附上一个自己YY的treap套树的复杂度证明吧:
由于treap是平衡的,所以O( h ) = O( log n ) ,这里为了方便,暂且将treap当成一棵满二叉树处理:
对于每次删除,期望旋转O(1)的证明:
如果删除的节点在第i层(从1标号到h),那么其旋转次数为(h-i),删除的节点在第i层的概率为( 2^( i - 1 ) ) / ( 2^h - 1 ),近似认为成( 2 ^( i - 1 ) ) / ( 2^h ) = 1 / ( 2^( h - i + 1 ) ),那么期望的旋转次数为:
即期望旋转次数不大于2次。
对于每次旋转,假如时间代价为所旋转节点的子树大小,那么其总期望代价为:
因此treap套树的复杂度是期望log n的。
代码:
#include
#include
#include
const int maxn = 110000 ;
inline void swap( int &x , int &y ) {
int z = x ; x = y ; y = z ;
}
inline int max( int x , int y ) {
return x > y ? x : y ;
}
#define L( t ) t -> left
#define R( t ) t -> right
#define S( t ) t -> size
#define maxv 31000000
int p0[ 20 ] ;
struct node {
node *left , *right ;
int size ;
} trie[ maxv ] ;
typedef node* pt ;
pt nll = trie , sta[ maxv ] , vt = trie ;
int cnt = 0 ;
void Init_trie( ) {
L( nll ) = R( nll ) = nll , S( nll ) = 0 ;
}
pt getn( ) {
pt x = cnt ? sta[ cnt -- ] : ++ vt ;
L( x ) = R( x ) = nll , S( x ) = 0 ;
return x ;
}
void recycle( pt t ) {
sta[ ++ cnt ] = t ;
if ( L( t ) != nll ) recycle( L( t ) ) ;
if ( R( t ) != nll ) recycle( R( t ) ) ;
}
inline void ins( int val , pt t ) {
for ( int i = 19 ; i >= 0 ; -- i ) if ( val & p0[ i ] ) {
if ( R( t ) == nll ) R( t ) = getn( ) ;
++ S( ( t = R( t ) ) ) ;
} else {
if ( L( t ) == nll ) L( t ) = getn( ) ;
++ S( ( t = L( t ) ) ) ;
}
}
inline void del( int val , pt t ) {
for ( int i = 19 ; i >= 0 ; -- i ) if ( val & p0[ i ] ) {
if ( ! ( -- S( R( t ) ) ) ) {
recycle( R( t ) ) ;
R( t ) = nll ;
return ;
} else t = R( t ) ;
} else {
if ( ! ( -- S( L( t ) ) ) ) {
recycle( L( t ) ) ;
L( t ) = nll ;
return ;
} else t = L( t ) ;
}
}
inline int query( int val , pt t ) {
int rec = 0 ;
for ( int i = 19 ; i >= 0 ; -- i ) {
rec <<= 1 ;
if ( val & p0[ i ] ) {
if ( S( L( t ) ) ) rec ^= 1 , t = L( t ) ; else t = R( t ) ;
} else {
if ( S( R( t ) ) ) rec ^= 1 , t = R( t ) ; else t = L( t ) ;
}
}
return rec ;
}
void merge( pt l , pt r , pt &t ) {
t = getn( ) ;
S( t ) = S( l ) + S( r ) ;
if ( S( L( l ) ) || S( L( r ) ) ) merge( L( l ) , L( r ) , L( t ) ) ;
if ( S( R( l ) ) || S( R( r ) ) ) merge( R( l ) , R( r ) , R( t ) ) ;
}
#undef maxv
#define maintain recycle( T( k ) ) ; T( k ) = T( t ) , S( k ) = S( t ) , FM( k ) = FM( t ) , SM( k ) = SM( t ) ; t -> update( ) ; t = k
#define maxv 301000
#define P( t ) t -> priority
#define FM( t ) t -> first_max
#define SM( t ) t -> second_max
#define W( t ) t -> weight
#define T( t ) t -> root
const int inf = 0x7fffffff ;
void upd0( int &x , int &y , int z ) {
if ( z > x ) {
y = x ; x = z ;
} else if ( z > y ) y = z ;
}
void upd1( int &x , int &y , int a , int b ) {
if ( a > x ) {
y = x > b ? x : b ;
x = a ;
} else if ( a > y ) y = a ;
}
struct Node {
Node *left , *right ;
int size , priority , weight , first_max , second_max ;
node *root ;
void update( ) {
size = left -> size + right -> size + 1 ;
first_max = left -> first_max , second_max = left -> second_max ;
upd1( first_max , second_max , right -> first_max , right -> second_max ) ;
upd0( first_max , second_max , weight ) ;
merge( left -> root , right -> root , root ) ;
ins( weight , root ) ;
}
} treap[ maxv ] ;
typedef Node* Pt ;
Pt Root = treap , Nll = treap , Vt = treap ;
void Init_treap( ) {
L( Nll ) = R( Nll ) = Nll , S( Nll ) = 0 , T( Nll ) = nll , P( Nll ) = FM( Nll ) = SM( Nll ) = W( Nll ) = - inf , srand( 19 ) ;
}
void Left( Pt &t ) {
Pt k = R( t ) ; R( t ) = L( k ) ; L( k ) = t ;
maintain ;
}
void Right( Pt &t ) {
Pt k = L( t ) ; L( t ) = R( k ) ; R( k ) = t ;
maintain ;
}
void Insert( int pos , int val , Pt &t ) {
if ( t == Nll ) {
t = ++ Vt ;
L( t ) = R( t ) = Nll , S( t ) = 1 , P( t ) = rand( ) , W( t ) = FM( t ) = val , SM( t ) = - inf , ins( val , T( t ) = getn( ) ) ;
return ;
}
++ S( t ) , ins( val , T( t ) ) , upd0( FM( t ) , SM( t ) , val ) ;
if ( pos <= S( L( t ) ) ) {
Insert( pos , val , L( t ) ) ;
if ( P( L( t ) ) > P( t ) ) Right( t ) ;
} else {
Insert( pos - S( L( t ) ) - 1 , val , R( t ) ) ;
if ( P( R( t ) ) > P( t ) ) Left( t ) ;
}
}
int Delete( int pos , Pt &t ) {
int s = S( L( t ) ) , w ;
if ( s == pos ) {
w = W( t ) ;
if ( L( t ) == Nll ) {
recycle( T( t ) ) ; t = R( t ) ; return w ;
} else if ( R( t ) == Nll ) {
recycle( T( t ) ) ; t = L( t ) ; return w ;
} else if ( P( L( t ) ) > P( R( t ) ) ) {
Right( t ) ; w = Delete( pos - S( L( t ) ) - 1 , R( t ) ) ;
} else {
Left( t ) ; w = Delete( pos , L( t ) ) ;
}
} else if ( pos < s ) w = Delete( pos , L( t ) ) ; else w = Delete( pos - s - 1 , R( t ) ) ;
del( w , T( t ) ) , -- S( t ) ;
FM( t ) = FM( L( t ) ) , SM( t ) = SM( L( t ) ) ;
upd0( FM( t ) , SM( t ) , W( t ) ) , upd1( FM( t ) , SM( t ) , FM( R( t ) ) , SM( R( t ) ) ) ;
return w ;
}
int Change( int pos , int val , Pt t ) {
int s = S( L( t ) ) , w ;
if ( s == pos ) {
w = W( t ) ; W( t ) = val ;
} else if ( pos < s ) w = Change( pos , val , L( t ) ) ; else w = Change( pos - s - 1 , val , R( t ) ) ;
ins( val , T( t ) ) ; del( w , T( t ) ) ;
FM( t ) = FM( L( t ) ) , SM( t ) = SM( L( t ) ) ;
upd0( FM( t ) , SM( t ) , W( t ) ) , upd1( FM( t ) , SM( t ) , FM( R( t ) ) , SM( R( t ) ) ) ;
return w ;
}
Pt NODE[ maxn ] ;
int w[ maxn ] , cntn , cntw ;
void Query( int l , int r , Pt t ) {
if ( ! l && r == S( t ) - 1 ) {
NODE[ ++ cntn ] = t ; return ;
}
int s = S( L( t ) ) ;
if ( r < s ) Query( l , r , L( t ) ) ; else
if ( l > s ) Query( l - s - 1 , r - s - 1 , R( t ) ) ; else {
w[ ++ cntw ] = W( t ) ;
Query( l , s - 1 , L( t ) ) , Query( 0 , r - s - 1 , R( t ) ) ;
}
}
inline int Solve( int l , int r ) {
cntn = cntw = 0 ;
Query( l , r , Root ) ;
int x = - inf , y = - inf , i , temp = 0 ;
for ( i = 1 ; i <= cntw ; ++ i ) upd0( x , y , w[ i ] ) ;
for ( i = 1 ; i <= cntn ; ++ i ) upd1( x , y , FM( NODE[ i ] ) , SM( NODE[ i ] ) ) ;
for ( i = 1 ; i <= cntw ; ++ i ) temp = max( temp , y ^ w[ i ] ) ;
for ( i = 1 ; i <= cntn ; ++ i ) temp = max( temp , query( y , T( NODE[ i ] ) ) ) ;
return temp ;
}
int n , m , a[ maxn ] , ans = 0 ;
void build( int l , int r , Pt &t ) {
t = ++ Vt ;
int mid = ( l + r ) >> 1 ;
W( t ) = a[ mid ] , S( t ) = 1 , P( t ) = rand( ) ;
if ( l < mid ) {
build( l , mid - 1 , L( t ) ) ;
if ( P( L( t ) ) > P( t ) ) swap( P( t ) , P( L( t ) ) ) ;
} else L( t ) = Nll ;
if ( r > mid ) {
build( mid + 1 , r , R( t ) ) ;
if ( P( R( t ) ) > P( t ) ) swap( P( t ) , P( R( t ) ) ) ;
} else R( t ) = Nll ;
t -> update( ) ;
}
int ch ;
void getint( int &t ) {
for ( ch = getchar( ) ; ch < '0' || ch > '9' ; ch = getchar( ) ) ;
t = ch - '0' ;
for ( ch = getchar( ) ; ch >= '0' && ch <= '9' ; ch = getchar( ) ) t = 10 * t + ch - '0' ;
}
int o[ 20 ] ;
inline void putint( int t ) {
if ( ! t ) putchar( '0' ) ; else {
o[ 0 ] = 0 ;
for ( ; t ; t /= 10 ) o[ ++ o[ 0 ] ] = t % 10 ;
while ( o[ 0 ] -- ) putchar( '0' + o[ o[ 0 ] + 1 ] ) ;
}
putchar( '\n' ) ;
}
int main( ) {
Init_trie( ) , Init_treap( ) ;
p0[ 0 ] = 1 ;
for ( int i = 1 ; i <= 19 ; ++ i ) p0[ i ] = p0[ i - 1 ] << 1 ;
getint( n ) , getint( m ) ;
for ( int i = 0 ; i ++ < n ; ) getint( a[ i ] ) ;
build( 1 , n , Root ) ;
int x , y ;
while ( m -- ) {
for ( ch = getchar( ) ; ch != 'I' && ch != 'D' && ch != 'C' && ch != 'F' ; ch = getchar( ) ) ;
if ( ch == 'I' ) {
getint( x ) , getint( y ) ;
x = ( x + ans ) % ( n ++ ) , y = ( y + ans ) % 1048576 ;
Insert( x , y , Root ) ;
} else if ( ch == 'D' ) {
getint( x ) ;
x = ( x + ans ) % ( n -- ) ;
Delete( x , Root ) ;
} else if ( ch == 'C' ) {
getint( x ) , getint( y ) ;
x = ( x + ans ) % n , y = ( y + ans ) % 1048576 ;
Change( x , y , Root ) ;
} else if ( ch == 'F' ) {
getint( x ) , getint( y ) ;
x = ( x + ans ) % n , y = ( y + ans ) % n ;
if ( x > y ) swap( x , y ) ;
printf( "%d\n" , ans = Solve( x , y ) ) ;
}
}
return 0 ;
}