大数据时代，参数怎么降维？

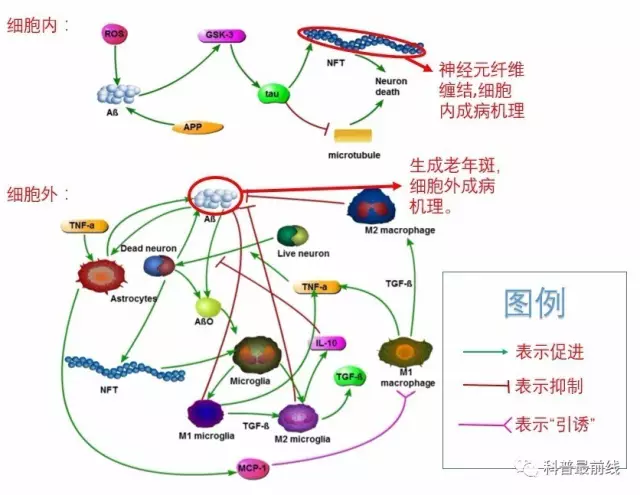
小编在《数学模型教你如何成为星际争霸高手·上篇》（传送门）[1]中提到过，参数估计（在数学上又称为反问题）往往比数学建模本身更为复杂。小编近日在研究阿尔兹海默症（Alzheimer's Disease，老年痴呆症的一种，已有上百年历史）的形成机制时对此深有体会。经多方总结，总算大体弄清楚了该病症的形成机理，得出如下图表[2]：

大家只需知道在这个复杂的网络中，每个小图都对应至少一个参数。看完后如果读者的表情是这样的：

小编表示理解，因为小编如果晚上睡不着，看看上面这个图表则倦意顿生！不一定非得“枕着你的名字才能入眠”，看着老年痴呆症的图表也可入眠。

其实以上图表已经经过了小编的高度简化，实际情景中还有许多未知或者有争议的致病机理尚待考证。所以用人名来命名一种疾病，实在是非常明智的，否则阿尔兹海默症应该译作——细胞质神经元纤维缠结-细胞外液β淀粉样蛋白老年斑致神经元萎缩疾病，以区别于其他老年痴呆症（帕金森综合症，ALS等）。每一种常见的疾病背后，都牵连着异常复杂的过程。

正好比当今中小学作业太多，需要减负；面对如此庞大（高维）的参数空间，自然也要想办法减少参数个数，这也是大数据时代普遍需要解决的问题。那么参数该如何降维呢？正所谓八仙过海各显神通，不同背景的科学家有不同的做法。

下图是参数估计问题的基本设定，

接下来的讨论都将基于这个设定。熟悉了以上设定，我们就可以出发了！

模型选择

数理统计学家对于模型参数的有关问题了如指掌，关于参数问题的方法和思想五花八门。例如在参数估计(Parameter Estimation)问题中，线性回归、非线性回归、极大似然估计是几种最常用的方法[3]。

不过在估计参数之前，首先要确定模型中到底需要多少参数。就像篮球比赛，参赛双方都有主力队员和替补队员，如果所有队员同时上场，势必造成场面混乱；如果双方只上一名队员，观赏性则远远不够。这就是模型选择(Model Selection)要解决的核心问题——到底派多少队员上场，才能既保证观赏性（模型的有效性），又不至于造成混乱（复杂性）呢？

模型参数，并非越多越好

在模型选择中，我们需要判断两种不同的参数选择方案和孰优孰劣。其核心思想便是寻找某种“度量”来衡量两种参数的表现，而经常使用的度量为优化R方检验(Adjusted R square)、AIC和BIC等。有兴趣的读者可以自行查询具体计算方法，这里只对这几种度量的特点进行比较：

可见这几种度量各有侧重，也各有好处。在实际应用中，这几种度量通常会同时派上用场，以对不同模型进行综合分析。

二、数据科学家提供思路——主成分分析

模型选择有个非常大的局限性，就是我们没有办法预先确定哪些参数相对有用，哪些无用，只有毫无规律地瞎猜。看样子这种方案不太行得通。

有没有办法能预先就判定出相对“有用”的参数呢？我们可以借鉴数据的降维方法，这可是数据科学家（本文的数据科学家更关注数据的处理和分析，数理统计学家更关注参数的处理和分析，两种思维是有差别的）的专长。其中最为出名的方法叫做主成分分析(Principle component analysis)。

什么叫高维数据呢？给定一个数据x，我们可以把这个数据看作一个向量，这个向量的每个分量都表示这个向量的某一个属性。例如“天气”，它由很多子属性构成——温度、湿度、降水量、能见度、风力、阳光强度、舒适度等等，于是这样一个简单的天气数据向量就包含了以上七个分量，是一个七维数据！就算是不了解数据分析的读者也可以看出，这个天气数据的七个分量之间存在着暧昧不清的关系，比如“湿度”必然和“降水量”有关，“舒适度”和前面几个分量都有关。那么能不能把“湿度”和“降水量”结合成一个新的分量？能不能把“舒适度”用其他分量表示？这就是数据的降维，也是主成分分析的基本思想，形成的新分量就是所谓的主成分。

如何把这种简单的思想翻译为精确的数学语言呢？简要地说，数学上用矩阵X（n×k，n是数据个数，k是数据维数，相当于把所有数据排列为一个矩阵）来表示高维数据的集合，称为设计矩阵(Design Matrix)。如果想提取数据的m个主成分，那么就通过计算矩阵X'X（X'表示X的转置，注意X'X是一个对称矩阵）的最大m个特征值对应的特征向量。而这m个特征向量则完全决定了前m个主成分的取法。

矩阵对角化。A若对称，那么P可以是正交阵，对角化相当于矩阵"旋转"

到此为止，数学家们已经心满意足了：“主成分嘛，不就是找对称矩阵的特征向量，用矩阵旋转的方法就可以搞定了！”但是数据科学家和计算科学家们还远不满足——实际计算中，矩阵对角化非常耗时耗力，例如要把一个k×k对称矩阵对角化，用QR分解的计算复杂度为O(k^3)[4]（读者可自己验证），在只需要很少几个主成分的情况下，这是没有必要的。于是通常的做法是先找出最大的特征值，得到相应的主成分，再按需要依次提取出更多的主成分。省时又省力，何乐而不为哉？计算复杂度是非常实际并且重要的概念，也是很多擅长理论的专家没有考虑过的因素，这也在一定程度上形成了理论界和应用界之间的鸿沟。

三、参数好坏的衡量——Fisher信息矩阵

回到对参数降维的问题。参数降维和数据降维之间是差异的——模型中的参数往往是满足限制条件的，而且和数据不一样，这些限制条件并不能直接用矩阵表示出来。这时候，熟悉数理统计的读者可能会联想到一个概念——极大似然估计中的Fisher信息矩阵(Fisher information matrix)，因为Fisher信息矩阵告诉了我们每个参数的估计方差。我们可以扔掉方差较大的参数（因为方差大，说明这个参数对模型影响小），至少得缩减它们在模型中的戏份。

我们来回顾一下极大似然估计的定义：

θ_MLE上面有一顶“帽子”，表示这是一个估计，一个随机变量，而非真实值。既然是随机变量，那么必然就有的误差，这种误差该如何衡量呢？当θ和x都是一维参数时，CR不等式（又名CR上界）告诉你答案：

也就是说估计误差由Fisher信息量所决定。其证明思想并不复杂，主要是利用柯西不等式和概率密度函数的性质。有兴趣的读者可以参考（这是小编四年前参加某数学竞赛面试时自创的方法，至今记忆犹新。时光荏苒，青葱岁月，现亲笔写下来，以作纪念）：

很久不写字，丑了许多（虽然原来也不好看）

当数据x维数增大时，θ（可以是高维参数）的极大似然估计满足中心极限定理（渐进正态），其协方差矩阵为Fisher信息矩阵的逆。

值得一提的是，“信息量”其实是借鉴了统计物理中的“熵”的概念[5]。有统计物理背景的读者会觉得Fisher信息量很眼熟。事实上，如果x是一个可观察值（量子力学中用Hermite算子表示，也就是在Hilbert中空间自共轭的算子），θ是x的共轭变量(Conjugate variable，如温度和熵、压强和体积、化学势能和粒子数都是共轭变量对)，那么x的不确定度（量子力学中的不确定度就是x的方差）正好由关于θ的Fisher信息矩阵给出[6]！小编还发现，如果把文献[6]的“共轭变量”推广到一般的量子哈密顿系统中去（例如动量-位置共轭和时间-能量共轭），那么海森堡测不准原理和CR不等式其实是等价的（唯一的区别在于由于物质波的假设，量子力学需要在复平面考虑问题。这个话题超过了本文范围，在以后的文章中继续介绍）！伟大的思想总是不谋而合，这个观点既有助于理解Fisher信息量，又能加强对量子世界的认识——这个世界是由一系列的不确定事件编织而成。

四、 黎曼几何登场

现在我们有了降维的思想——主成分分析，有了衡量参数好坏的方法——Fisher信息量，那么接下来该如何操作呢？一种大胆的想法是，把这些参数看作是高维空间中的低维曲面（更准确的说法是流形，但为了简单起见，本文依然使用“曲面”的概念），然后通过某种方式让Fisher信息量来决定这个曲面的具体形状，以决定这个参数空间的限定条件，从而达到参数降维的目的。这个想法正是一个新兴学科——信息几何学（Information geometry）的基本思想。而Fisher信息量充当的角色，正是黎曼度量（Riemann metric）。

三维空间中的二维曲面

小编在初学微分几何的曲面论时，遇到了不小的麻烦。当时不知道黎曼度量到底是何方神圣，所有在曲面上的分析都是利用所谓“第一基本形式”和“第二基本形式”的概念来完成的。例如曲面上两点间的测地线(geodesic)，是指曲面上连接两点的最短曲线。这个概念虽然简单，但当老师从容不迫地推导了一黑板测地线方程

图片来自网络

时，小编是崩溃的，尤其是那几个“christoffel符号”（最后一行的Γ项，既有上指标又有两个项指标）。尽管曲面论的出发点是很符合直观的，但推导过程非常复杂，往往使初学者把注意力集中在每一项的具体数学形式是什么，而不是对每个符号的直观理解，而过于复杂的公式很容易让人产生畏惧心理。这是分析思想的特点之一——出发点符合直观，但过程可能很繁杂。

但当小编学过黎曼几何后，所有的问题仿佛都迎刃而解了。黎曼几何的出发点看似很抽象——它直接把曲面本身看做一个度量空间，而黎曼度量则被定义为一个正定矩阵（或者正定二次型，例如欧式空间的黎曼度量是单位矩阵）。有了黎曼度量，所有的概念都渐渐地透明起来，例如那些全身上下挂满指标的“christoffel符号”，在黎曼几何中又被称为Levi-Civita联络，是由于曲面的弯曲特性，把曲面上对向量场的微分计算转化到欧式空间时（因为我们熟悉的微积分都是定义在在欧式空间上的，需要做此转化），需要添加的修正项。

从这个观点出发（见上图），我们就不难理解为什么测地线方程会出现Levi-Civita联络了。测地线，说穿了就是对曲面上连接两点的所有曲线的总长（这个总长和黎曼度量有关）求最小值，只需要对研究向量场的变化即可。对向量场求微分以后，Levi-Civita联络随之出现，造就了简约而不简单的测地线方程。尽管出发点颇为抽象，曲面论中很多看似复杂的定义在黎曼几何中得到了更为清晰的诠释，因而黎曼几何更符合代数思想——抽象，但是思路清晰且具备高度概括性。

抽象归抽象，参数估计这个看似不那么抽象的工作还是要继续的。既然我们有了测地线的概念，那么是不是可以从参数曲面上任意一点（初始值）出发，沿着测地线方向行走，达到降维或者优化的目的呢？这正是信息几何学的要害所在！从K维参数曲面上的一点出发，沿着测地线行走到曲面的边界处（注意边界规定了参数的取值范围，通常是人为给定的），我们就走到了K-1维的曲面上，从而参数空间变成了K-1维！如果在这个K-1维曲面上继续沿着测地线行走到它的边界，那么我们就走到了K-2维曲面上。以此类推，就达到了参数降维的目的！具体算法如下图所示[7]：

算法的可视化，偏应用的读者只需记住这张图即可，不必拘泥于具体理论推导

从直观上看来，信息几何学中的降维思想和主成分分析颇为相似——都是通过对某个正定矩阵作变换来达到一步步降维的目的，每一次迭代后参数或数据都会发生“旋转”。不同之处在于，1. 参数曲面上的黎曼度量会随着曲面发生连续变化，所以参数需要沿着测地线“旋转”；2. 每次发生“旋转”后，参数的维数会减小一维，而数据的旋转得到的只是一维主成分。同是降维，两者的降维方向是不同的。

不过也许“旋转”这个概念能帮助读者从另一个角度理解Levi-Civita联络的意义。

今后我们还可以逐渐看到，黎曼几何的概念直接推动了整个20世纪物理和数学多个分支的蓬勃发展，并且把一些看似毫无关系的思想串联了起来。例如群表示论、李代数、微分方程、同调论、拓扑度理论等数学工具得以被直接运用于黎曼流形（更一般地，复流形）及其对应的纤维从上，构成了规范场论（坐标变换的推广，通常用群作用表示）、量子场论（为统一量子力学和广义相对论而设）和标准模型（把除了引力以外的力和各种基本粒子统一起来）等物理理论的雏形[7-11]，这是代数思想的又一个伟大意义。当然，这是题外话。

五、总结

通过对几种不同的思想比较，我们可以切身体会到对数据降维和对参数降维的巨大差异，总结如下：

因此参数分析和数据分析是两个完全不同的概念，运用的方法也大相径庭，这也是为什么小编要在第二节中把数据科学家和数理统计学家区分开来。值得一提的是，虽然流形学习(Manifold learning)也是数据降维的主要处理手段之一，但是和信息几何学全然不同，因为主流的流形学习技术中并没有黎曼度量的概念，更不需要考虑数据应该朝哪个方向降维（参数则沿着测地线降维）的问题。不过显然，了解信息几何学的基本思想，有助于加强对流形学习的认识。

作为数理统计、统计物理和黎曼几何三种不同智慧的结晶，信息几何学是解决参数降维问题的一个极为强大的工具。它至少有四个优点：

这么一个强有力的工具，为何知道的人并不多呢？原因也很简单。其一，这是一个很年轻的学科，很多理论尚处于发展期；其二，起点太高，至少需要同时掌握数理统计和黎曼几何两种思想（统计力学的观点也很重要，解释了为什么Fisher信息矩阵可以看做黎曼度量），在工业界应用受限；其三，不同人对信息几何的理解不同，例如文献[12]，更多的是把数理统计和机器学习中的概念用几何语言重新表述一遍，并没有实际应用案例。本文的观点则是基于文献[6]和[13]。

伟大的思想之所以能够不谋而合，是因为它们内在的普适性和抽象性，也就是小编一直所推崇的代数思想。估计很少有人能够想到，黎曼几何的概念不仅能对现代物理学产生颠覆性的转变，而且还能在参数估计这种应用界难题上发挥作用。英雄并不孤单，那么有没有其他像黎曼几何这样的“英雄”存在呢？答案是肯定的，不过每个“英雄”都有自己亲自谱写的史诗级篇章，以后小编将会一一道来。最后以一首诗来总结本文，以加深读者的记忆。

参数降维行

千金易散，知己难求；模型易得，参数难测。

参数既估，繁若迷糊。欲求清净，亟访名师。

岳王庙口，西湖斜畔，统计泰斗，参禅指手。

模型茫茫，筛而选之。安以定度？称量先拓。

姑苏城郊，红尘声嚣。数据学者，殊无隔阂。

银汉虽广，太白引航；数据虽多，缘其脉搏。

数据固庞，主干分明；参数稍贫，层次难寻。

信息矩阵，相助解困。主次参差，呼之渐晰。

参数常匿，降维何易。黎曼几何，释疑颂歌。

信息度量，测地线网，参数曲面，万物具全。

统计出谋，数据划策，几何导领，天下安定。

如果喜欢小编的文章，就长按下面的二维码关注小编的公众号吧！

参考文献：

[1] https://mp.weixin.qq.com/s?__biz=MzIyNjc2NzY4OA==&mid=2247483777&idx=1&sn=27ec78f138b1fa74d81a6fdf7c712976&chksm=e86a27a6df1daeb03c1265a2d88a4f0c466b3de2b2ddacf17dfa6a427582ff0bc55e7d7cee8a#rd

[2] W. Hao et. al, Mathematical model on Alzheimer’s disease.

[3] S. Chatterjee et. al, Regression analysis by example, 5th edition.

[4] J.W. Demmel et. al, Performance and Accuracy of LAPACK's Symmetric Tridiagonal Eigensolvers.

[5] http://mp.weixin.qq.com/s/sNtzlDbGfSE3j_H3cLJNdA.

[6] G.E. Crooks Measuring thermodynamic length.

[7] 马天, 流形拓扑学：理论与概念的实质。

[8] 马天, 从数学观点看物理世界——几何分析，引力场与相对论.

[9] 马天, 从数学观点看物理世界——基本粒子与统一场理论。

[10] F. Lachello, Lie algebras and applications.

[11] L.P. Horwitz, Relativistic quantum mechanics.

[12] S. Amari, Information Geometry and Its Applications.

[13] M.K. Transtrum et. al, Sloppiness and emergent theories in physics, biology, and beyond.