- Bash 命令:系统操作的得力助手
阿贾克斯的黎明
运维bash开发语言
目录Bash命令:系统操作的得力助手目录操作命令文件操作命令文件查看命令在Linux系统的日常使用与运维工作中,Bash命令起着核心作用。它就像一把万能钥匙,能够开启系统各种功能的大门,让我们高效地管理和操作计算机资源。接下来,我们将详细介绍一些常用的Bash命令及其用法。目录操作命令ls(list):用于列出目录内容。例如,在终端输入ls,会显示当前目录下的文件和子目录。如果要查看详细信息,可以
- C++中“::”与“.”的区别
阿贾克斯的黎明
C++c++
在C++编程中,“::”(作用域解析运算符)和“.”(成员访问运算符)是两个非常重要的符号,但它们有着不同的用途和功能。一、“.”成员访问运算符“.”用于访问类、结构体或联合体对象的成员。以下是一个简单的示例:#includeclassMyClass{public:intmemberVariable;voidmemberFunction(){std::coutnamespaceMyNamespac
- 深度学习笔记——前向传播与反向传播、神经网络(前馈神经网络与反馈神经网络)、常见算法概要汇总
好评笔记
深度学习笔记深度学习笔记神经网络人工智能
大家好,这里是好评笔记,公主号:Goodnote,专栏文章私信限时Free。本文简要介绍深度学习的前向传播与反向传播,以及前馈神经网络与反馈神经网络。文章目录前向传播与反向传播前向传播(ForwardPropagation)反向传播(BackPropagation)总结神经网络简介结构类型前馈神经网络(FeedforwardNeuralNetwork,FFNN)特点常见变体反馈神经网络(Feedb
- 机器学习笔记——Boosting中常用算法(GBDT、XGBoost、LightGBM)迭代路径
好评笔记
机器学习笔记机器学习boosting人工智能深度学习AI算法工程师
大家好,这里是好评笔记,公主号:Goodnote,专栏文章私信限时Free。本文主要阐述Boosting中常用算法(GBDT、XGBoost、LightGBM)的迭代路径。文章目录XGBoost相对GBDT的改进引入正则化项,防止过拟合损失函数L(yi,y^i)L(y_i,\hat{y}_i)L(yi,y^i)正则化项Ω(fm)\Omega(f_m)Ω(fm)使用二阶导数信息,加速收敛一阶导数与二
- Knowledge Boundary of Large Language Models: A Survey
UnknownBody
LLMDailySurveyPaper语言模型人工智能自然语言处理
本文是LLM系列文章,针对《KnowledgeBoundaryofLargeLanguageModels:ASurvey》的翻译。大型语言模型的知识边界:综述摘要1引言2知识边界的定义3不良行为4知识边界的识别5缓解6挑战与前景7结论局限性摘要尽管大型语言模型(LLM)在其参数中存储了大量的知识,但它们在记忆和利用某些知识方面仍然存在局限性,导致了不良的行为,如产生不真实和不准确的反应。这突显了理
- CS4398 Cirrus Logic的旗舰级音频解码芯片
中国芯xinsousou
CirrusLogic(凌云)音频解码芯片单片机可用性测试
CS4398是一块24Bit/192KHz规格的解码芯片,它具有120分贝以上的讯噪比和动态范围,总谐波失真+噪声低至0.0005%,采用一个高级专用多位Delta-Sigma调制器,并整合了失配噪声整形技术。CS4398是一个完整的立体声24位/192kHz数模系统。该D/A系统包括数字去加重,半dB步长音量控制,ATAPI通道混合,可选的快速和慢速数字插值滤波器,再加上过采样的多位delta-
- 十几套JavaWeb项目,快拿去当毕业设计,简直不要太爽了
VX_BYDZ1988
djangoflaskeclipsespringbootspringcloudservlet
1、基于web的图书管理系统设计与实现图书管理系统就是利用计算机,结合互联网对图书进行结构化、自动化管理的一种软件,来提高对图书的管理效率。本系统采用Java+Servlet+Jsp的方式实现基于web的图书管理系统。开发工具及相关技术Java技术HTML、css、javascript技术Servlet技术Eclipse开发工具MySql数据库功能概述用户端:图书查询:根据图书编号、图书名称查询图
- RPA财务机器人是什么,RPA的具体应用场景有哪些?| 实在RPA研究
实在智能RPA
rpa机器人自动化人工智能数字员工
越来越多的人工智能及超自动化技术在企业财务工作中得以普及应用,以提升财务工作效率,促进财务部门实现全面数字化转型。RPA财务机器人是什么?RPA,即机器人流程自动化(RoboticProcessAutomation),允许软件机器人(或“机器人”)自动执行重复性、规律性强的业务流程任务。RPA软件机器人可以模仿人类用户的行为,通过用户界面与应用程序交互,执行任务如数据输入、报告生成、数据迁移、邮件
- RPA 机器人到底有啥用?一文全知晓
RPAdaren
rpa机器人自动化ai
在当今数字化飞速发展的时代,RPA(机器人流程自动化)技术正逐渐崭露头角,成为各行业提升效率、优化流程的得力助手。那么,RPA机器人究竟有啥用呢?让我们一起来深入探究。一、RPA如何成为企业的智能助手(一)精准模仿人类操作,开启自动化之旅RPA机器人宛如一位训练有素的数字助手,其核心能力便是精准地模仿人类在计算机系统中的各种操作行为。它就像一个细心的观察者,能够记录下用户在诸如企业资源规划系统ER
- 软体机器人研究报告:设计方法、材料与驱动、感知与控制
MocapLeader
软体机器人连续体机器人手术机器人运动规划运动控制游泳机器人人工肌肉
软体机器人因其出色的可变形性和高适应性受到了广泛关注,这些特性使其在医疗、救援、探测等复杂场景中展现出独特的优势和巨大的应用潜力。研究人员对软体机器人的设计方法、材料与驱动技术、感知与控制策略等方面进行深入研究,取得了一系列成果。本文汇总了10项软体机器人领域的优秀研究成果,并介绍了不同成果的研究亮点。在下述研究中,NOKOV度量动作捕捉系统通过实时记录机器人的运动过程、获取高精度空间定位,为实验
- 2023全国职业院校技能大赛网络系统管理赛项(Linux部分真题)
Jackson~Y
linux运维服务器
一、Linux项目任务描述你作为一个Linux的技术工程师,被指派去构建一个公司的内部网络,要为员工提供便捷、安全稳定内外网络服务。你必须在规定的时间内完成要求的任务,并进行充分的测试,确保设备和应用正常运行。任务所有规划都基于Linux操作系统,请根据网络拓扑、基本配置信息和服务需求完成网络服务安装与测试,网络拓扑图和基本配置信息如下:(一)拓扑图(二)网络地址规划服务器和客户端基本配置如下表,
- 北大数学校友胡懿娟归国任教!重回母校,专注于统计学、微生物学和遗传学的交叉领域
量子位
关注前沿科技量子位又一科学家从美归国——北大数学系校友胡懿娟。援引人民日报消息,在北京大学北京国际数学研究中心发布的2024年工作回顾中显示,她于去年7月入职北大。回来之后,她将继续专注于统计学、微生物学和遗传学的交叉领域,致力于解决实际的生物医学数据分析问题。△北大官网截图网友纷纷为她点赞:能力与颜值并存!同时也感叹,越来越多的科学家选择回到祖国,为科学技术发展和人才培养添砖加瓦。北大数学校友胡
- 全球人形机器人的创新发展与未来趋势
Gearidea
机器人机器人
随着科技的迅猛进步,人形机器人作为人工智能与机器人技术交汇的产物,正在全球范围内引发广泛关注。人形机器人以其仿人的外观和行为,不仅在工业生产领域展现出巨大的潜力,而且在日常生活中也逐渐发挥着不可忽视的作用。本文将全面剖析全球人形机器人的发展现状,展望未来发展的潜在趋势,并深入探讨其在不同领域中的应用和影响。一、全球人形机器人行业的发展现状全球人形机器人领域经历了从概念提出、原型制作到商业化应用的演
- 财务RPA,财务RPA机器人的应用场景有哪些?
弘玑RPA智能机器人
rpa
众所周知,机器人流程自动化RPA在过去几年中得到了快速发展。现在,已经可以实现端到端完全自动化流程,并可以利用智能自动化扩展RPA部署。目前RPA机器人在金融与银行、保险、电力、能源、制造业、公共服务、零售、业务流程外包/共享中心等行业中广泛应用。本文将重点讲一下财务RPA机器人在金融银行业的使用场景。相对于传统的人工办公,财务RPA机器人对于金融机构意味几何?加快合规减少成本和合规积压提高运营效
- LeetCode:3097. 或值至少为 K 的最短子数组 II(滑动窗口 Java)
Cosmoshhhyyy
LeetCodeleetcodejava算法
目录3097.或值至少为K的最短子数组II题目描述:实现代码与解析:滑动窗口原理思路:3097.或值至少为K的最短子数组II题目描述:给你一个非负整数数组nums和一个整数k。如果一个数组中所有元素的按位或运算OR的值至少为k,那么我们称这个数组是特别的。请你返回nums中最短特别非空子数组的长度,如果特别子数组不存在,那么返回-1。示例1:输入:nums=[1,2,3],k=2输出:1解释:子数
- Python字典详解
2401_89224765
python开发语言
print(dict4)需要注意的是:fromkeys方法只用来创建新字典,不负责保存。当通过一个字典来调用fromkeys方法时,如果需要后续使用一定记得给他复制给其他的变量。②访问字典:第一阶段:基操勿6!如果要想获取字典中某个键的值,可以通过访问键的方式来显示对应的值。上代码:dict={‘线代’:“99”,“数据分析”:“99”,“概率论”:“98”}#创建字典print(‘小红同学的线代
- 回顾 2024— 浔川社团:在数字浪潮中的成长与奋进
浔川社团官方联合会
浔川社团官方联合会总社团联合会浔川python社推广部python
回顾2024—浔川社团:在数字浪潮中的成长与奋进在过去的2024年,浔川社团以其独特的魅力和不懈的努力,在网络的舞台上绽放出别样的光彩。从各项数据指标中,我们能清晰地看到社团这一年来的发展轨迹,见证其在内容创作、社区互动等方面所取得的斐然成绩。一、流量数据:持续攀升的影响力截至2024年底,浔川社团相关内容的总访问量达到了74,556次,这一数字直观地反映出社团所产出内容的广泛吸引力。无论是技术分
- 使用Python爬虫将抓取的数据保存到Excel文件
Python爬虫项目
2025年爬虫实战项目python爬虫excel测试工具开发语言信息可视化
在进行Python爬虫开发时,数据的存储是非常重要的一环。随着数据分析需求的不断增长,保存和管理大量的数据变得尤为重要。CSV(Comma-SeparatedValues)格式一直是一个常见的存储格式,但在许多应用场景下,Excel文件作为一种更直观、结构化的方式,具有更多的优势,尤其在数据分析与可视化方面。Excel文件不仅能够承载数据,还能进行复杂的数据操作、图表展示等,使其在数据科学、商业分
- 工业互联网体系架构:赋能制造业转型升级
2201_75335682
架构
摘要:随着全球信息化和工业化进程的加快,工业互联网作为新一代信息技术与制造业深度融合的产物,已成为推动我国制造业转型升级的重要力量。本文将从工业互联网体系架构的内涵、特点、关键技术及发展策略等方面进行详细阐述,以期为我国工业互联网的健康发展提供参考。一、工业互联网体系架构内涵工业互联网体系架构主要包括四个层次:感知层、传输层、平台层和应用层。感知层负责实时采集设备、环境和人员等信息;传输层通过有线
- Python测试的艺术:深入理解单元测试与unittest框架应用
清水白石008
开发语言Python题库pythonpython单元测试开发语言
Python测试的艺术:深入理解单元测试与unittest框架应用一、引言在软件开发过程中,测试是确保软件质量的关键环节。Python作为一种流行的编程语言,其测试体系也非常成熟和强大。其中,单元测试是测试体系中最基础、最常用的一种。本文将详细介绍单元测试的概念,并使用Python的内置测试框架unittest来编写一个简单的测试用例,帮助读者理解并掌握单元测试的基本方法和技巧。二、单元测试概述单
- Playwright 精通系列第五篇:表单处理与文件上传/下载
weixin_44872675
Playwright深入学习python
在自动化测试中,表单操作和文件上传/下载是两大常见需求。表单操作不仅包括输入框和按钮的交互,还涉及到单选框、多选框、下拉菜单等复杂组件。而文件上传和下载更是许多用户测试流程中的难点,尤其是在处理非标准化的文件组件时。本篇文章将深入探讨表单处理和文件上传/下载的核心功能,结合实战案例,列举常见问题和解决思路,帮助你更高效地完成自动化测试。1.Playwright表单处理的优势链式操作简洁高效:Pla
- python内置函数之type() 函数
凯凯恺恺恺恺凯凯
python之内置函数
文章目录type()函数描述语法参数返回值实例isinstance()与type()区别:type()函数描述type()函数如果你只有第一个参数则返回对象的类型,三个参数返回新的类型对象。语法以下是type()方法的语法:type(object)type(name,bases,dict)参数name–类的名称。bases–基类的元组。dict–字典,类内定义的命名空间变量。返回值一个参数返回对象
- python 函数_Python type() 函数
weixin_39622217
python函数
Pythontype()函数描述Pythontype()函数如果你只有第一个参数则返回对象的类型,三个参数返回新的类型对象。isinstance()与type()区别:type()不会认为子类是一种父类类型,不考虑继承关系。isinstance()会认为子类是一种父类类型,考虑继承关系。如果要判断两个类型是否相同推荐使用isinstance()。语法以下是type()方法的语法:type(obje
- Web的基本架构
ssdljwdxml
前端web
随着互联网的普及和发展,Web已经成为人们获取信息、交流和娱乐的主要方式之一。而支撑着这个庞大网络世界的就是Web的基本架构。本文将深入探讨Web的基本架构,包括客户端、服务器、网络协议等核心组件,以及它们之间的交互关系。一、客户端客户端是用户直接与之交互的界面,可以是浏览器或其他支持Web的应用程序。浏览器是最常见的客户端,它负责向服务器发送请求并接收服务器返回的响应。当用户在浏览器中输入一个网
- 【AIcoding技术必知必会】12问--前后端联调是什么?
srzxy42
AIcoding技术必知必会ai产品经理学习
基础说明前后端联调(Frontend-BackendIntegration)是指前端工程师和后端工程师将各自开发的功能模块进行对接和测试的过程。这个过程确保前端页面能够正确地与后端API进行数据交互,实现完整的业务功能。具体步骤准备阶段前后端团队共同制定接口文档(APIDocumentation)确定接口的请求方式(GET/POST等)定义请求参数和返回数据格式(通常是JSON)约定接口的命名规范
- springMVC文件上传和下载
xls丶
springmvc
[置顶]SpringMVC单文件上传、多文件上传、文件列表显示、文件下载标签:SpringMVC文件上传文件下载列表显示2015-05-1821:0122627人阅读评论(6)收藏举报分类:SpringMVC(8)作者同类文章X•Shrio登陆验证实例详细解读•Spring+Mybatis+SpringMVC后台与前台分页展示实例(附工程)•Spring+Mybatis+SpringMVC+Mav
- Elasticsearch二次开发:实现实时定时同步同义词、近义词与停用词
codeBrute
elasticsearch中文分词
Elasticsearch二次开发:实现实时定时同步同义词、近义词与停用词引言Elasticsearch(ES)作为开源搜索引擎的典范,以其强大的全文搜索、结构化搜索以及分析能力,在各个领域得到了广泛应用。在复杂的搜索场景中,同义词、近义词和停用词的处理对于提升搜索的准确性和用户体验至关重要。为了满足动态变化的业务需求,实现同义词、近义词与停用词的定时同步成为了一项关键任务。本文将详细介绍如何在E
- MySQL SQL优化技巧与原理
codeBrute
关系型数据库sql
前言随着业务数据量的不断增加,MySQL查询语句的执行效率对程序的运行效率影响逐渐增大。因此,进行SQL优化变得至关重要。本文将结合SQL的执行语句顺序和各种SQL场景,介绍一些常见的MySQLSQL优化技巧及其背后的原理。一、MySQLSQL执行语句顺序MySQLSQL的执行顺序通常分为以下步骤:FROM子句:加载表,计算笛卡尔积,生成虚拟表VT1。ON子句:筛选关联表符合ON表达式的数据,生成
- 算法设计与分析第一章课后作业
小毛头~
算法
第一章一.单选题1【单选题】子程序(包括函数和方法)是用来被调用的,递归指的是A、不同子程序之间直接或间接调用的程序设计方法B、同一个子程序直接或间接调用自己的程序设计方法C、子程序向调用它的程序段返回结果的程序设计方法D、子程序不向调用它的程序段返回结果的程序设计方法正确答案:B我的答案:B得分:4.0分2【单选题】背包问题:n个物品和1个背包。对物品i,其价值为vi,重量为wi,背包的容量为W
- .NET Core Web API架构解析:应用场景与实例详解
m0_74824054
.netcore前端架构
“.NETCoreWebAPI架构深度解析:实战应用场景与代码示例”内容概述引言简要介绍.NETCore和WebAPI的基本概念。阐述本文的目的:深入解析.NETCoreWebAPI的架构,探讨其在实际项目中的应用场景,并提供代码示例。.NETCoreWebAPI架构解析核心组件:介绍ASP.NETCore框架中的关键组件,如Kestrel服务器、中间件管道、路由等。MVC模式:在WebAPI中的
- 设计模式介绍
tntxia
设计模式
设计模式来源于土木工程师 克里斯托弗 亚历山大(http://en.wikipedia.org/wiki/Christopher_Alexander)的早期作品。他经常发表一些作品,内容是总结他在解决设计问题方面的经验,以及这些知识与城市和建筑模式之间有何关联。有一天,亚历山大突然发现,重复使用这些模式可以让某些设计构造取得我们期望的最佳效果。
亚历山大与萨拉-石川佳纯和穆雷 西乐弗斯坦合作
- android高级组件使用(一)
百合不是茶
androidRatingBarSpinner
1、自动完成文本框(AutoCompleteTextView)
AutoCompleteTextView从EditText派生出来,实际上也是一个文本编辑框,但它比普通编辑框多一个功能:当用户输入一个字符后,自动完成文本框会显示一个下拉菜单,供用户从中选择,当用户选择某个菜单项之后,AutoCompleteTextView按用户选择自动填写该文本框。
使用AutoCompleteTex
- [网络与通讯]路由器市场大有潜力可挖掘
comsci
网络
如果国内的电子厂商和计算机设备厂商觉得手机市场已经有点饱和了,那么可以考虑一下交换机和路由器市场的进入问题.....
这方面的技术和知识,目前处在一个开放型的状态,有利于各类小型电子企业进入
&nbs
- 自写简单Redis内存统计shell
商人shang
Linux shell统计Redis内存
#!/bin/bash
address="192.168.150.128:6666,192.168.150.128:6666"
hosts=(${address//,/ })
sfile="staticts.log"
for hostitem in ${hosts[@]}
do
ipport=(${hostitem
- 单例模式(饿汉 vs懒汉)
oloz
单例模式
package 单例模式;
/*
* 应用场景:保证在整个应用之中某个对象的实例只有一个
* 单例模式种的《 懒汉模式》
* */
public class Singleton {
//01 将构造方法私有化,外界就无法用new Singleton()的方式获得实例
private Singleton(){};
//02 申明类得唯一实例
priva
- springMvc json支持
杨白白
json springmvc
1.Spring mvc处理json需要使用jackson的类库,因此需要先引入jackson包
2在spring mvc中解析输入为json格式的数据:使用@RequestBody来设置输入
@RequestMapping("helloJson")
public @ResponseBody
JsonTest helloJson() {
- android播放,掃描添加本地音頻文件
小桔子
最近幾乎沒有什麽事情,繼續鼓搗我的小東西。想在項目中加入一個簡易的音樂播放器功能,就像華為p6桌面上那麼大小的音樂播放器。用過天天動聽或者QQ音樂播放器的人都知道,可已通過本地掃描添加歌曲。不知道他們是怎麼實現的,我覺得應該掃描設備上的所有文件,過濾出音頻文件,每個文件實例化為一個實體,記錄文件名、路徑、歌手、類型、大小等信息。具體算法思想,
- oracle常用命令
aichenglong
oracledba常用命令
1 创建临时表空间
create temporary tablespace user_temp
tempfile 'D:\oracle\oradata\Oracle9i\user_temp.dbf'
size 50m
autoextend on
next 50m maxsize 20480m
extent management local
- 25个Eclipse插件
AILIKES
eclipse插件
提高代码质量的插件1. FindBugsFindBugs可以帮你找到Java代码中的bug,它使用Lesser GNU Public License的自由软件许可。2. CheckstyleCheckstyle插件可以集成到Eclipse IDE中去,能确保Java代码遵循标准代码样式。3. ECLemmaECLemma是一款拥有Eclipse Public License许可的免费工具,它提供了
- Spring MVC拦截器+注解方式实现防止表单重复提交
baalwolf
spring mvc
原理:在新建页面中Session保存token随机码,当保存时验证,通过后删除,当再次点击保存时由于服务器端的Session中已经不存在了,所有无法验证通过。
1.新建注解:
? 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
- 《Javascript高级程序设计(第3版)》闭包理解
bijian1013
JavaScript
“闭包是指有权访问另一个函数作用域中的变量的函数。”--《Javascript高级程序设计(第3版)》
看以下代码:
<script type="text/javascript">
function outer() {
var i = 10;
return f
- AngularJS Module类的方法
bijian1013
JavaScriptAngularJSModule
AngularJS中的Module类负责定义应用如何启动,它还可以通过声明的方式定义应用中的各个片段。我们来看看它是如何实现这些功能的。
一.Main方法在哪里
如果你是从Java或者Python编程语言转过来的,那么你可能很想知道AngularJS里面的main方法在哪里?这个把所
- [Maven学习笔记七]Maven插件和目标
bit1129
maven插件
插件(plugin)和目标(goal)
Maven,就其本质而言,是一个插件执行框架,Maven的每个目标的执行逻辑都是由插件来完成的,一个插件可以有1个或者几个目标,比如maven-compiler-plugin插件包含compile和testCompile,即maven-compiler-plugin提供了源代码编译和测试源代码编译的两个目标
使用插件和目标使得我们可以干预
- 【Hadoop八】Yarn的资源调度策略
bit1129
hadoop
1. Hadoop的三种调度策略
Hadoop提供了3中作业调用的策略,
FIFO Scheduler
Fair Scheduler
Capacity Scheduler
以上三种调度算法,在Hadoop MR1中就引入了,在Yarn中对它们进行了改进和完善.Fair和Capacity Scheduler用于多用户共享的资源调度
2. 多用户资源共享的调度
- Nginx使用Linux内存加速静态文件访问
ronin47
Nginx是一个非常出色的静态资源web服务器。如果你嫌它还不够快,可以把放在磁盘中的文件,映射到内存中,减少高并发下的磁盘IO。
先做几个假设。nginx.conf中所配置站点的路径是/home/wwwroot/res,站点所对应文件原始存储路径:/opt/web/res
shell脚本非常简单,思路就是拷贝资源文件到内存中,然后在把网站的静态文件链接指向到内存中即可。具体如下:
- 关于Unity3D中的Shader的知识
brotherlamp
unityunity资料unity教程unity视频unity自学
首先先解释下Unity3D的Shader,Unity里面的Shaders是使用一种叫ShaderLab的语言编写的,它同微软的FX文件或者NVIDIA的CgFX有些类似。传统意义上的vertex shader和pixel shader还是使用标准的Cg/HLSL 编程语言编写的。因此Unity文档里面的Shader,都是指用ShaderLab编写的代码,然后我们来看下Unity3D自带的60多个S
- CopyOnWriteArrayList vs ArrayList
bylijinnan
java
package com.ljn.base;
import java.util.ArrayList;
import java.util.Iterator;
import java.util.List;
import java.util.concurrent.CopyOnWriteArrayList;
/**
* 总述:
* 1.ArrayListi不是线程安全的,CopyO
- 内存中栈和堆的区别
chicony
内存
1、内存分配方面:
堆:一般由程序员分配释放, 若程序员不释放,程序结束时可能由OS回收 。注意它与数据结构中的堆是两回事,分配方式是类似于链表。可能用到的关键字如下:new、malloc、delete、free等等。
栈:由编译器(Compiler)自动分配释放,存放函数的参数值,局部变量的值等。其操作方式类似于数据结构中
- 回答一位网友对Scala的提问
chenchao051
scalamap
本来准备在私信里直接回复了,但是发现不太方便,就简要回答在这里。 问题 写道 对于scala的简洁十分佩服,但又觉得比较晦涩,例如一例,Map("a" -> List(11,111)).flatMap(_._2),可否说下最后那个函数做了什么,真正在开发的时候也会如此简洁?谢谢
先回答一点,在实际使用中,Scala毫无疑问就是这么简单。
- mysql 取每组前几条记录
daizj
mysql分组最大值最小值每组三条记录
一、对分组的记录取前N条记录:例如:取每组的前3条最大的记录 1.用子查询: SELECT * FROM tableName a WHERE 3> (SELECT COUNT(*) FROM tableName b WHERE b.id=a.id AND b.cnt>a. cnt) ORDER BY a.id,a.account DE
- HTTP深入浅出 http请求
dcj3sjt126com
http
HTTP(HyperText Transfer Protocol)是一套计算机通过网络进行通信的规则。计算机专家设计出HTTP,使HTTP客户(如Web浏览器)能够从HTTP服务器(Web服务器)请求信息和服务,HTTP目前协议的版本是1.1.HTTP是一种无状态的协议,无状态是指Web浏览器和Web服务器之间不需要建立持久的连接,这意味着当一个客户端向服务器端发出请求,然后We
- 判断MySQL记录是否存在方法比较
dcj3sjt126com
mysql
把数据写入到数据库的时,常常会碰到先要检测要插入的记录是否存在,然后决定是否要写入。
我这里总结了判断记录是否存在的常用方法:
sql语句: select count ( * ) from tablename;
然后读取count(*)的值判断记录是否存在。对于这种方法性能上有些浪费,我们只是想判断记录记录是否存在,没有必要全部都查出来。
- 对HTML XML的一点认识
e200702084
htmlxml
感谢http://www.w3school.com.cn提供的资料
HTML 文档中的每个成分都是一个节点。
节点
根据 DOM,HTML 文档中的每个成分都是一个节点。
DOM 是这样规定的:
整个文档是一个文档节点
每个 HTML 标签是一个元素节点
包含在 HTML 元素中的文本是文本节点
每一个 HTML 属性是一个属性节点
注释属于注释节点
Node 层次
- jquery分页插件
genaiwei
jqueryWeb前端分页插件
//jquery页码控件// 创建一个闭包 (function($) { // 插件的定义 $.fn.pageTool = function(options) { var totalPa
- Mybatis与Ibatis对照入门于学习
Josh_Persistence
mybatisibatis区别联系
一、为什么使用IBatis/Mybatis
对于从事 Java EE 的开发人员来说,iBatis 是一个再熟悉不过的持久层框架了,在 Hibernate、JPA 这样的一站式对象 / 关系映射(O/R Mapping)解决方案盛行之前,iBaits 基本是持久层框架的不二选择。即使在持久层框架层出不穷的今天,iBatis 凭借着易学易用、
- C中怎样合理决定使用那种整数类型?
秋风扫落叶
c数据类型
如果需要大数值(大于32767或小于32767), 使用long 型。 否则, 如果空间很重要 (如有大数组或很多结构), 使用 short 型。 除此之外, 就使用 int 型。 如果严格定义的溢出特征很重要而负值无关紧要, 或者你希望在操作二进制位和字节时避免符号扩展的问题, 请使用对应的无符号类型。 但是, 要注意在表达式中混用有符号和无符号值的情况。
&nbs
- maven问题
zhb8015
maven问题
问题1:
Eclipse 中 新建maven项目 无法添加src/main/java 问题
eclipse创建maevn web项目,在选择maven_archetype_web原型后,默认只有src/main/resources这个Source Floder。
按照maven目录结构,添加src/main/ja
- (二)androidpn-server tomcat版源码解析之--push消息处理
spjich
javaandrodipn推送
在 (一)androidpn-server tomcat版源码解析之--项目启动这篇中,已经描述了整个推送服务器的启动过程,并且把握到了消息的入口即XmppIoHandler这个类,今天我将继续往下分析下面的核心代码,主要分为3大块,链接创建,消息的发送,链接关闭。
先贴一段XmppIoHandler的部分代码
/**
* Invoked from an I/O proc
- 用js中的formData类型解决ajax提交表单时文件不能被serialize方法序列化的问题
中华好儿孙
JavaScriptAjaxWeb上传文件FormData
var formData = new FormData($("#inputFileForm")[0]);
$.ajax({
type:'post',
url:webRoot+"/electronicContractUrl/webapp/uploadfile",
data:formData,
async: false,
ca
- mybatis常用jdbcType数据类型
ysj5125094
mybatismapperjdbcType
MyBatis 通过包含的jdbcType
类型
BIT FLOAT CHAR
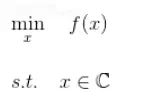
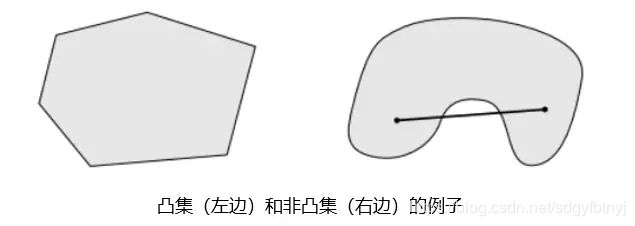 即要求目标函数是凸函数,变量所属集合是凸集合的优化问题。或者目标函数是凸函数,变量的约束函数是凸函数(不等式约束时),或者是仿射函数(等式约束时)。
即要求目标函数是凸函数,变量所属集合是凸集合的优化问题。或者目标函数是凸函数,变量的约束函数是凸函数(不等式约束时),或者是仿射函数(等式约束时)。