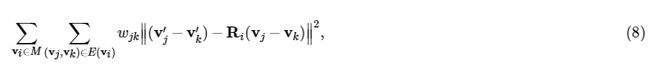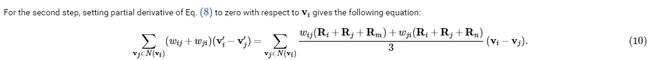CGAL 4.9 - Triangulated Surface Mesh Deformation

Here, I would like to derive the formula (10)

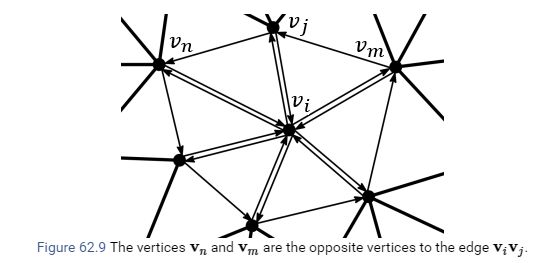
For triangle vjvivm , we have the following three equation which is related to vi

wij∥(v′i−v′j)−Ri(vi−vj)∥2
wij∥(v′i−v′j)−Rj(vi−vj)∥2
wij∥(v′i−v′j)−Rm(vi−vj)∥2

The same as for for triangle vivjvn we have:

wji∥(v′j−v′i)−Ri(vi−vj)∥2
wji∥(v′j−v′i)−Rj(vi−vj)∥2
wji∥(v′j−v′i)−Rn(vi−vj)∥2

Taking derivative of those equations w.r.t vi and sum them up yields formula (10)

Then, let us look into alec jacobson’s matlab code

 function K = spokes_and_rims_linear_block(V,F,d)
    % Computes a matrix K such that K * R computes
    %  鈭�   -2*(cot(aij) + cot(bij) * (V(i,d)-V(j,d)) * (Ri + Rj) +
    %       -2*cot(aij) * (V(i,d)-V(j,d)) * Raij +
    %       -2*cot(bij) * (V(i,d)-V(j,d)) * Rbij
    % j鈭圢(i)
    % 
    % where:          vj
    %              /  |  \
    %             /   |   \
    %            /    |    \
    %           /     |     \
    %          aij    |    bij
    %           \     |     /
    %            \    |    /
    %             \fij|gij/
    %              \  |  /
    %                 vi
    % 
    % Inputs:
    %   V  #V by dim list of coordinates
    %   F  #F by 3 list of triangle indices into V
    %   d  index into columns of V
    % Output:
    %   K  #V by #F matrix
    %
    if simplex_size == 3
      % triangles
      C = cotangent(V,F);
      i1 = F(:,1); i2 = F(:,2); i3 = F(:,3);
      I = [i1;i2;i2;i3;i3;i1;i1;i2;i3];
      J = [i2;i1;i3;i2;i1;i3;i1;i2;i3];
      v = [ ...
         C(:,3).*(V(i1,d)-V(i2,d)) + C(:,2).*(V(i1,d)-V(i3,d)); ... 
        -C(:,3).*(V(i1,d)-V(i2,d)) + C(:,1).*(V(i2,d)-V(i3,d)); ... 
         C(:,1).*(V(i2,d)-V(i3,d)) + C(:,3).*(V(i2,d)-V(i1,d)); ... 
        -C(:,1).*(V(i2,d)-V(i3,d)) + C(:,2).*(V(i3,d)-V(i1,d)); ... 
         C(:,2).*(V(i3,d)-V(i1,d)) + C(:,1).*(V(i3,d)-V(i2,d)); ... 
        -C(:,2).*(V(i3,d)-V(i1,d)) + C(:,3).*(V(i1,d)-V(i2,d)); ... 
         ... % diagonal
        C(:,3).*(V(i1,d)-V(i2,d)) - C(:,2).*(V(i3,d)-V(i1,d)); ... 
        C(:,1).*(V(i2,d)-V(i3,d)) - C(:,3).*(V(i1,d)-V(i2,d)); ... 
        C(:,2).*(V(i3,d)-V(i1,d)) - C(:,1).*(V(i2,d)-V(i3,d)); ... 
        ];
      % construct and divide by 3 so laplacian can be used as is
      K = sparse(I,J,v,n,n)/3;
    elseif simplex_size == 4
      % tetrahedra
      assert(false)
    end
  end

The column dimension of matrix k goes through each vertex that edges connect to. Elements on each row of matrix k are the same for linearizing the rotation matrix summation.
For each vertex on each triangle, we sum cot* edge up through edges connected to it.