Unity动画关键帧插值
Unity动画的关键帧插值有2种模式1,一种是3次多项式插值,另一种是3次贝塞尔曲线插值。下面介绍具体实现,首先我们先看关键帧的几个重要成员定义:
inTangent,左侧的斜率,下面用it来表示
inWeight,决定贝塞尔曲线的第2个点的x,用iw表示
outTangent,右侧的斜率,用ot表示
outWeight,决定贝塞尔曲线第3个点的x,用ow表示
value,关键帧的值,用y表示
time,关键帧的时间,用x表示
给定两个关键帧,
F i = { i t i , i w i , o t i , o w i , x i , y i } , 0 ≤ i ≤ 1 F_i = \{ it_i, iw_i, ot_i, ow_i, x_i, y_i \},\ 0 \le i \le 1 Fi={iti,iwi,oti,owi,xi,yi}, 0≤i≤1
三次多项式插值
三次多项式插值在两个关键帧的weightedMode都是None时使用。
三次多项式方程为
y = f ( x ) = a x 3 + b x 2 + c x + d y = f(x) = ax^3+bx^2+cx+d y=f(x)=ax3+bx2+cx+d
我们可以使用如下4个方程解得4个系数
{ f ( x 0 ) = y 0 f ( x 1 ) = y 1 f ′ ( x 0 ) = o t 0 f ′ ( x 1 ) = i t 1 \begin{cases} f(x_0) = y_0 & \\ f(x_1) = y_1 & \\ f'(x_0) = ot_0 & \\ f'(x_1) = it_1 \end{cases} ⎩⎪⎪⎪⎨⎪⎪⎪⎧f(x0)=y0f(x1)=y1f′(x0)=ot0f′(x1)=it1
得到的结果以矩阵表示为
[ a b c d ] = [ x 0 3 x 0 2 x 0 1 x 1 3 x 1 2 x 1 1 3 x 0 2 2 x 0 1 0 3 x 1 2 2 x 1 1 0 ] − 1 [ y 0 y 1 o t 0 i t 1 ] \begin{bmatrix} a \\ b \\c \\d \end{bmatrix} = \begin{bmatrix} x_0^3 & x_0^2 & x_0 & 1 \\ x_1^3 & x_1^2 & x_1 & 1 \\ 3x_0^2 & 2x_0 & 1 & 0 \\ 3x_1^2 & 2x_1 & 1 & 0 \end{bmatrix}^{-1} \begin{bmatrix} y_0 \\ y_1 \\ ot_0 \\ it_1 \end{bmatrix} ⎣⎢⎢⎡abcd⎦⎥⎥⎤=⎣⎢⎢⎡x03x133x023x12x02x122x02x1x0x1111100⎦⎥⎥⎤−1⎣⎢⎢⎡y0y1ot0it1⎦⎥⎥⎤
计算逆矩阵比较麻烦,我们可以将曲线的区间平移并规格化到 [ 0 , 1 ] [0,1] [0,1]中再做计算,这样就方便许多,新的方程组为
{ f ( 0 ) = y 0 f ( 1 ) = y 1 f ′ ( 0 ) = o t 0 ( x 1 − x 0 ) f ′ ( 1 ) = i t 1 ( x 1 − x 0 ) \begin{cases} f(0) = y_0 & \\ f(1) = y_1 & \\ f'(0) = ot_0 (x_1 - x_0) & \\ f'(1) = it_1 (x_1 - x_0) \end{cases} ⎩⎪⎪⎪⎨⎪⎪⎪⎧f(0)=y0f(1)=y1f′(0)=ot0(x1−x0)f′(1)=it1(x1−x0)
注意,由于进行了缩放,端点处的斜率也需要进行缩放。
解得
[ a b c d ] = [ ( o t 0 + i t 1 ) ( x 1 − x 0 ) − 2 ( y 1 − y 0 ) ( − 2 o t 0 − i t 1 ) ( x 1 − x 0 ) + 3 ( y 1 − y 0 ) o t 0 ( x 1 − x 0 ) y 0 ] \begin{bmatrix} a \\ b \\c \\d \end{bmatrix} = \begin{bmatrix} (ot_0+it_1)(x_1-x_0)-2(y_1-y_0) \\ (-2ot_0-it_1) (x_1 - x_0) + 3(y_1-y_0) \\ ot_0(x_1-x_0) \\ y_0 \end{bmatrix} ⎣⎢⎢⎡abcd⎦⎥⎥⎤=⎣⎢⎢⎡(ot0+it1)(x1−x0)−2(y1−y0)(−2ot0−it1)(x1−x0)+3(y1−y0)ot0(x1−x0)y0⎦⎥⎥⎤
给定时间 t t t,我们可以使用如下公式得到插值的结果
f ( t − x 0 x 1 − x 0 ) f(\frac{t-x_0}{x_1-x_0}) f(x1−x0t−x0)
我们验证一下结果,给定两个关键帧2
F 0 = { 0 , 1 3 , 0 , 1 3 , 0 , 0 } F 1 = { 0 , 1 3 , 0 , 1 3 , 1 , 1 } F_0 = \{0,\frac{1}{3},0,\frac{1}{3},0,0\} \\ F_1 = \{0,\frac{1}{3},0,\frac{1}{3},1,1\} F0={0,31,0,31,0,0}F1={0,31,0,31,1,1}
该多项式实际为
y = − 2 x 3 + 3 x 2 y=-2x^3+3x^2 y=−2x3+3x2
对glsl熟悉的朋友应该会对这个多项式不陌生,就是smoothstep所用hermite多项式。
unity中的曲线为

在unity中查看 1 / 3 1/3 1/3, 2 / 3 2/3 2/3处的结果为
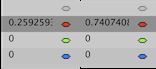
我们再看一下代入多项式后的值
f ( 1 3 ) = 7 27 = 0.2592592593 f ( 2 3 ) = 20 27 = 0.7407407407 f(\frac{1}{3}) = \frac{7}{27} = 0.2592592593 \\ f(\frac{2}{3}) = \frac{20}{27} = 0.7407407407 f(31)=277=0.2592592593f(32)=2720=0.7407407407
结果是一致的。
贝塞尔曲线插值
多项式插值不使用inWeight和outWeight,根据unity文档
Sets the incoming weight for this key. The incoming weight affects the slope of the curve from the previous key to this key.
第一想法是使用了贝塞尔曲线一类的插值方法。
三次贝塞尔曲线需要4个点,而这里4个点的定义如下
P 0 = ( x 0 , y 0 ) P 1 = ( x 0 + o w 0 ( x 1 − x 0 ) , y 0 + o w 0 ⋅ o t 0 ( x 1 − x 0 ) P 2 = ( x 1 − i w 1 ( x 1 − x 0 ) , y 1 − i w 1 ⋅ i t 1 ( x 1 − x 0 ) P 3 = ( x 1 , y 1 ) \begin{aligned} P_0 &= (x_0,y_0) \\ P_1 &= (x_0 + ow_0(x_1-x_0),y_0+ow_0\cdot ot_0 (x_1-x_0) \\ P_2 &= (x_1 - iw_1(x1-x_0),y_1-iw_1\cdot it_1 (x_1 - x_0) \\ P_3 &= (x_1,y_1) \end{aligned} P0P1P2P3=(x0,y0)=(x0+ow0(x1−x0),y0+ow0⋅ot0(x1−x0)=(x1−iw1(x1−x0),y1−iw1⋅it1(x1−x0)=(x1,y1)
这里 i w iw iw和 o w ow ow用来决定中间点的 x x x坐标,且权重在 [ 0 , 1 ] [0,1] [0,1]内。
我们来验证一下,给定如下两个关键帧(我们需要将Tangent设置为Weighted)
F 0 = { 0 , 1 3 , − 1 , 1 , 0 , 0 } F 1 = { 0 , 1 3 , − 0.5 , 0.5 , 1 , 1 } \begin{aligned} F_0 &= \{0,\frac{1}{3},-1,1,0,0\} \\ F_1 &= \{0,\frac{1}{3},-0.5,0.5,1,1\} \end{aligned} F0F1={0,31,−1,1,0,0}={0,31,−0.5,0.5,1,1}
在unity中查看 1 / 3 1/3 1/3, 2 / 3 2/3 2/3处的结果为

由于贝塞尔曲线不是以 x x x为参数的曲线,我们需要先解得对应参数 t t t,之后再代入得到 y y y。三次方程有封闭解,具体见Wikipedia。
解得对应的两个 t t t以及 y y y为
t 0 = 0.1371916262 y 0 = − 0.2429122496 t 1 = 0.4502223408 y 1 = 0.1009137022 \begin{aligned} t_0 &= 0.1371916262 \\ y_0 &=-0.2429122496 \\ t_1 &= 0.4502223408\\ y_1 &= 0.1009137022 \end{aligned} t0y0t1y1=0.1371916262=−0.2429122496=0.4502223408=0.1009137022
可以看到与editor中的结果一致。
默认权重
当一个关键帧的weightedMode不是weighted时,此时会默认采用 1 / 3 1/3 1/3作为权重,该权重为unity默认写入的值,通过观察clip文件可知。
官方文档没有给出具体算法,贝塞尔曲线插值只是猜测。 ↩︎
其中的权重 1 3 \frac{1}{3} 31会在贝塞尔曲线插值中讲到 ↩︎
