目录
- 从DBC到JML
- SMT solver 使用
- JML toolchain的可视化输出 和我的测试结果
- 规格的完善策略
- 架构设计
- debug情况
- 心得体会
一、从DBC到JML
契约式设计(Design by Contract)是一种开发软件的新思路。不妨通过商业活动的中真实的Contract(契约)来理解这个例子:
- 供应商必须提供某种产品(这是供应商的义务),并且有权期望客户付费(这是供应商的权利)。
- 客户必须支付费用(这是客户的义务),并且有权得到产品(这是客户的权利)。
- 双方必须满足应用于合约的某些义务,如法律和规定。
那我们可以从程序设计的角度看需要哪些契约呢:
- 可接受和不可接受的输入的值或类型,以及它们的含义
- 返回的值或类型,以及它们的含义
- 错误和异常的值或类型,以及它们的含义
- 副作用
- 先验条件
- 后验条件
- 不变性
- (不太常见)性能保证,例如所需的时间和空间。我在后文中建立了性能相关的规格约定模式。
可以说JML是为DBC而生的(或者在学术上称之为DBC语言)。
我们从JML的原生语法来看,就非常符合契约设计的理念:
- requires 描述先验条件
- ensures 描述后验条件
- old 描述和消除副作用
- exceptional_behavior 描述错误和异常
所以说JML是教学和学术研究中对于DBC理论探索的一个利器。
形式化<->可以消除歧义。
形式化<->可以被程序读取!
形式化<->可以自动分析和推导!
这样,不仅写代码的人可以准确读懂需求,测试人员可以从测试上透视功能!
二、SMT solver 使用
笔者的java SMT代码一览,采用Microsoft Z3 SMT solver
void prove(Context ctx, BoolExpr f, boolean useMBQI) throws TestFailedException
{
BoolExpr[] assumptions = new BoolExpr[0];
prove(ctx, f, useMBQI, assumptions);
}
void prove(Context ctx, BoolExpr f, boolean useMBQI,
BoolExpr... assumptions) throws TestFailedException
{
System.out.println("Proving: " + f);
Solver s = ctx.mkSolver();
Params p = ctx.mkParams();
p.add("mbqi", useMBQI);
s.setParameters(p);
for (BoolExpr a : assumptions)
s.add(a);
s.add(ctx.mkNot(f));
Status q = s.check();
switch (q)
{
case UNKNOWN:
System.out.println("Unknown because: " + s.getReasonUnknown());
break;
case SATISFIABLE:
throw new TestFailedException();
case UNSATISFIABLE:
System.out.println("OK, proof: " + s.getProof());
break;
}
}
void disprove(Context ctx, BoolExpr f, boolean useMBQI)
throws TestFailedException
{
BoolExpr[] a = {};
disprove(ctx, f, useMBQI, a);
}
void disprove(Context ctx, BoolExpr f, boolean useMBQI,
BoolExpr... assumptions) throws TestFailedException
{
System.out.println("Disproving: " + f);
Solver s = ctx.mkSolver();
Params p = ctx.mkParams();
p.add("mbqi", useMBQI);
s.setParameters(p);
for (BoolExpr a : assumptions)
s.add(a);
s.add(ctx.mkNot(f));
Status q = s.check();
switch (q)
{
case UNKNOWN:
System.out.println("Unknown because: " + s.getReasonUnknown());
break;
case SATISFIABLE:
System.out.println("OK, model: " + s.getModel());
break;
case UNSATISFIABLE:
throw new TestFailedException();
}
}
跑一个简单的数独验证先测试一下SMT 在本地有效(代码来自官方template,有很多改动)
void sudokuExample(Context ctx) throws TestFailedException
{
System.out.println("SudokuExample");
Log.append("SudokuExample");
// 9x9 matrix of integer variables
IntExpr[][] X = new IntExpr[9][];
for (int i = 0; i < 9; i++)
{
X[i] = new IntExpr[9];
for (int j = 0; j < 9; j++)
X[i][j] = (IntExpr) ctx.mkConst(
ctx.mkSymbol("x_" + (i + 1) + "_" + (j + 1)),
ctx.getIntSort());
}
// each cell contains a value in {1, ..., 9}
BoolExpr[][] cells_c = new BoolExpr[9][];
for (int i = 0; i < 9; i++)
{
cells_c[i] = new BoolExpr[9];
for (int j = 0; j < 9; j++)
cells_c[i][j] = ctx.mkAnd(ctx.mkLe(ctx.mkInt(1), X[i][j]),
ctx.mkLe(X[i][j], ctx.mkInt(9)));
}
// each row contains a digit at most once
BoolExpr[] rows_c = new BoolExpr[9];
for (int i = 0; i < 9; i++)
rows_c[i] = ctx.mkDistinct(X[i]);
// each column contains a digit at most once
BoolExpr[] cols_c = new BoolExpr[9];
for (int j = 0; j < 9; j++)
cols_c[j] = ctx.mkDistinct(X[j]);
// each 3x3 square contains a digit at most once
BoolExpr[][] sq_c = new BoolExpr[3][];
for (int i0 = 0; i0 < 3; i0++)
{
sq_c[i0] = new BoolExpr[3];
for (int j0 = 0; j0 < 3; j0++)
{
IntExpr[] square = new IntExpr[9];
for (int i = 0; i < 3; i++)
for (int j = 0; j < 3; j++)
square[3 * i + j] = X[3 * i0 + i][3 * j0 + j];
sq_c[i0][j0] = ctx.mkDistinct(square);
}
}
BoolExpr sudoku_c = ctx.mkTrue();
for (BoolExpr[] t : cells_c)
sudoku_c = ctx.mkAnd(ctx.mkAnd(t), sudoku_c);
sudoku_c = ctx.mkAnd(ctx.mkAnd(rows_c), sudoku_c);
sudoku_c = ctx.mkAnd(ctx.mkAnd(cols_c), sudoku_c);
for (BoolExpr[] t : sq_c)
sudoku_c = ctx.mkAnd(ctx.mkAnd(t), sudoku_c);
// sudoku instance, we use '0' for empty cells
int[][] instance = { { 0, 0, 0, 0, 9, 4, 0, 3, 0 },
{ 0, 0, 0, 5, 1, 0, 0, 0, 7 }, { 0, 8, 9, 0, 0, 0, 0, 4, 0 },
{ 0, 0, 0, 0, 0, 0, 2, 0, 8 }, { 0, 6, 0, 2, 0, 1, 0, 5, 0 },
{ 1, 0, 2, 0, 0, 0, 0, 0, 0 }, { 0, 7, 0, 0, 0, 0, 5, 2, 0 },
{ 9, 0, 0, 0, 6, 5, 0, 0, 0 }, { 0, 4, 0, 9, 7, 0, 0, 0, 0 } };
BoolExpr instance_c = ctx.mkTrue();
for (int i = 0; i < 9; i++)
for (int j = 0; j < 9; j++)
instance_c = ctx.mkAnd(
instance_c,
(BoolExpr) ctx.mkITE(
ctx.mkEq(ctx.mkInt(instance[i][j]),
ctx.mkInt(0)), ctx.mkTrue(),
ctx.mkEq(X[i][j], ctx.mkInt(instance[i][j]))));
Solver s = ctx.mkSolver();
s.add(sudoku_c);
s.add(instance_c);
if (s.check() == Status.SATISFIABLE)
{
Model m = s.getModel();
Expr[][] R = new Expr[9][9];
for (int i = 0; i < 9; i++)
for (int j = 0; j < 9; j++)
R[i][j] = m.evaluate(X[i][j], false);
System.out.println("Sudoku solution:");
for (int i = 0; i < 9; i++)
{
for (int j = 0; j < 9; j++)
System.out.print(" " + R[i][j]);
System.out.println();
}
} else
{
System.out.println("Failed to solve sudoku");
throw new TestFailedException();
}
}
用SMT solver 很难测试像图论这样的问题,所以我的策略是先测试一个经典的数独问题,如上。
此外我做了两个测试:
- 验证连通块个数实验
这种验证确实非常高级非常有效,但是写代码还是相当长的,(包括生成代码和模板代码)。
测试用代码如下
private BoolExpr generate(BinopExpr expr) {
BoolExpr ret = null;
if(expr instanceof ConditionExpr){
//get two sides and the operator
ConditionExpr condExpr = (ConditionExpr)expr;
//lhs can either be constant or a local
//12-29-14, not right now when we
//have more general formula
Value lhs = condExpr.getOp1();
IntExpr lhsExpr = evaluateExpr(lhs);
//rhs can also be an arithmetic expression
//from converting assignments to equality
Value rhs = condExpr.getOp2();
ArithExpr rhsExpr = null;
//add conditionals here first to check
if(rhs instanceof BinopExpr){
BinopExpr rhsBinop = (BinopExpr) rhs;
IntExpr lhsArith = evaluateExpr(rhsBinop.getOp1());
IntExpr rhsArith = evaluateExpr(rhsBinop.getOp2());
//now determine the operator add, sub, mult
try {
if(rhsBinop instanceof AddExpr){
ArithExpr[] operands = new ArithExpr[]{lhsArith, rhsArith};
rhsExpr = ctx.MkAdd(operands);
} else if (rhsBinop instanceof SubExpr){
ArithExpr[] operands = new ArithExpr[]{lhsArith, rhsArith};
rhsExpr = ctx.MkSub(operands);
} else if (rhsBinop instanceof MulExpr){
ArithExpr[] operands = new ArithExpr[]{lhsArith, rhsArith};
rhsExpr = ctx.MkMul(operands);
} else if (rhsBinop instanceof DivExpr){
rhsExpr = ctx.MkDiv(lhsArith, rhsArith);
} else if(rhsBinop instanceof RemExpr){
rhsExpr = ctx.MkMod(lhsArith, rhsArith);
} else if (rhsBinop instanceof ShrExpr){
//can only handle when rhs,i.e., y is not a variable
// x >> y = x / (2^y)
if(rhsArith.IsArithmeticNumeral()){
IntNum number = (IntNum)rhsArith;
rhsArith = ctx.MkInt(1<- 验证多个最短路算法的等价性
此外,部分代码在python下(验证)_
三、JML toolchain 用于测试
目前JML的工具有这些:
- ESC/Java2 1, an extended static checker which uses JML annotations to perform more rigorous static checking than is otherwise possible.
- OpenJML declares itself the successor of ESC/Java2.
- Daikon, a dynamic invariant generator.
- KeY, which provides an open source theorem prover with a JML front-end and an Eclipse plug-in (JML Editing) with support for syntax highlighting of JML.
- Krakatoa, a static verification tool based on the Why verification platform and using the Coq proof assistant.
- JMLEclipse, a plugin for the Eclipse integrated development environment with support for JML syntax and interfaces to various tools that make use of JML annotations.
- Sireum/Kiasan, a symbolic execution based static analyzer which supports JML as a contract language.
- JMLUnit, a tool to generate files for running JUnit tests on JML annotated Java files.
- TACO, an open source program analysis tool that statically checks the compliance of a Java program against its Java Modeling Language specification.
- VerCors verifier
但是这些工具并不能满足我的开发和证明要求,由于我后续加入,我自行开发了一个命令行工具 Advanced JML check with TesTNG ( AJCT )。(功能很不完善)。
其原理其实是OpenJML + JMLUnitNG + jprofiler + Python + Bash 的一个组合脚本。
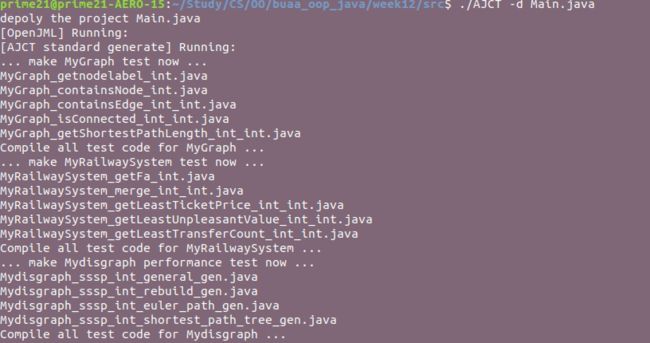
生成结果如下
.
├── AJCT
├── Main.java
├── Mydisgraph.java
├── Mydisgraph_sssp_int_euler_path_gen.class
├── Mydisgraph_sssp_int_euler_path_gen.java
├── Mydisgraph_sssp_int_general_gen.class
├── Mydisgraph_sssp_int_general_gen.java
├── Mydisgraph_sssp_int_rebuild_gen.class
├── Mydisgraph_sssp_int_rebuild_gen.java
├── Mydisgraph_sssp_int_shortest_path_tree_gen.class
├── Mydisgraph_sssp_int_shortest_path_tree_gen.java
├── MyGraph_containsEdge_int_int.class
├── MyGraph_containsEdge_int_int.java
├── MyGraph_containsNode_int.class
├── MyGraph_containsNode_int.java
├── MyGraph_getnodelabel_int.class
├── MyGraph_getnodelabel_int.java
├── MyGraph_getShortestPathLength_int_int.class
├── MyGraph_getShortestPathLength_int_int.java
├── MyGraph_isConnected_int_int.class
├── MyGraph_isConnected_int_int.java
├── MyGraph.java
├── MyNode.java
├── MyPathContainer.java
├── MyPath.java
├── MyRailwaySystem_getFa_int.class
├── MyRailwaySystem_getFa_int.java
├── MyRailwaySystem_getLeastTicketPrice_int_int.class
├── MyRailwaySystem_getLeastTicketPrice_int_int.java
├── MyRailwaySystem_getLeastTransferCount_int_int.class
├── MyRailwaySystem_getLeastTransferCount_int_int.java
├── MyRailwaySystem_getLeastUnpleasantValue_int_int.class
├── MyRailwaySystem_getLeastUnpleasantValue_int_int.java
├── MyRailwaySystem.java
├── MyRailwaySystem_merge_int_int.class
└── MyRailwaySystem_merge_int_int.java
四、规格完善策略
我发现了现有的规格体系的一个缺点:即无法保证描述方法的时空间复杂度,因此,我在此基础上,加入了关于复杂度的描述规格,用于测试我自己的代码。
(目前,我的规格只能测试图的最短路算法和图论其他基本算法。)
我的复杂度规格描述策略如下:
- pre-condition: 表示算法中某一些集合,和他们的大小范围。
- parameter: 表示参数属于算法中的哪一个集合,和他们的大小范围。
- time complexity: 用时间复杂度的标准形式,要求有 online, offline, worst-case几个关键描述。(省略大O记号)
- space complexity: 用空间复杂度的标准形式。
这部分的开发过程有很多困难,由于还没有彻底完善,不方便开源(还在做进一步测试)。
引入这个规格的考虑有如下考量:
-
后续重构要考量该接口是否会丧失原有性能、导致各种问题(进程不同步、需求无法满足)。
-
对调用者友好,能不用透视代码,而从性能和功能两个层次考量是否调用该方法、调用的条件是什么。
-
对验证有效,工程问题的正确性和效率(开发效率、测试效率)都和基本的性能要求分不开,能提前做好性能的规格设计,在没有遇到性能问题之前大概率无需顾虑。
-
性能规格可以做理论推导、可以通过调用方法和后续方法的性能规格推导该规格的bound,做到防御性设计。
关于我的性能测试报告可以看我的优化博客,在此只做简要的叙述。
在性能测试阶段,利用多种输入情况对程序的运行时间情况做拟合,得到的表达式和规格表达式对比,从而得到验证复杂度的效果。
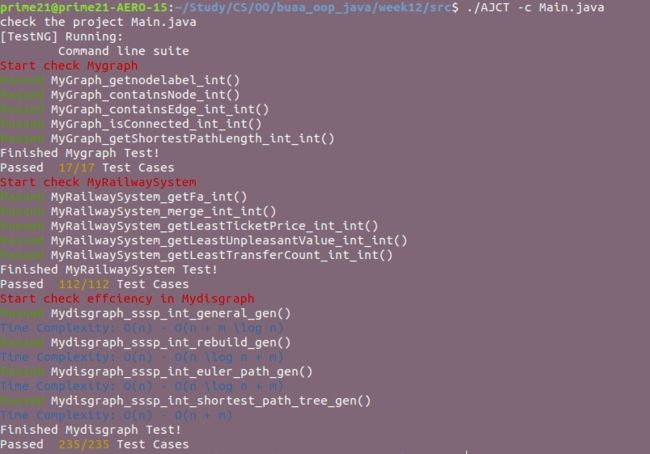
我的验证结果如下
利用
\(f(n) - g(n)\) 这样的表达式表达:修改复杂度为\(f(n)\),询问复杂度为\(g(n)\)
| algo \ case | general gen | rebuild gen | Euler path gen | shortest path tree gen |
|---|---|---|---|---|
| A-star-algorithm | \(O(n^2)-O(n+m)\) | \(O(n^2)-O(n+m)\) | \(O(n^2)-O(n+m)\) | \(O(n+m)-O(n+m)\) |
| \(O(n^2)\) transfer line algorithm | \(O(n^2)-O(m)\) | \(O(n^2)-O(m)\) | \(O(n^2)-O(m)\) | \(O(n^2)-O(m)\) |
| my algorithm | $O(n)-O(n + m \log n) $ | $O(n)-O(n \log n + m) $ | $O(n)-O(n \log n + m) $ | $O(n)-O(n + m) $ |
| floyd algorithm | $O(n^3)-O(1) $ | $O(n^3)-O(1) $ | $O(n^3)-O(1) $ | $O(n^3)-O(1) $ |
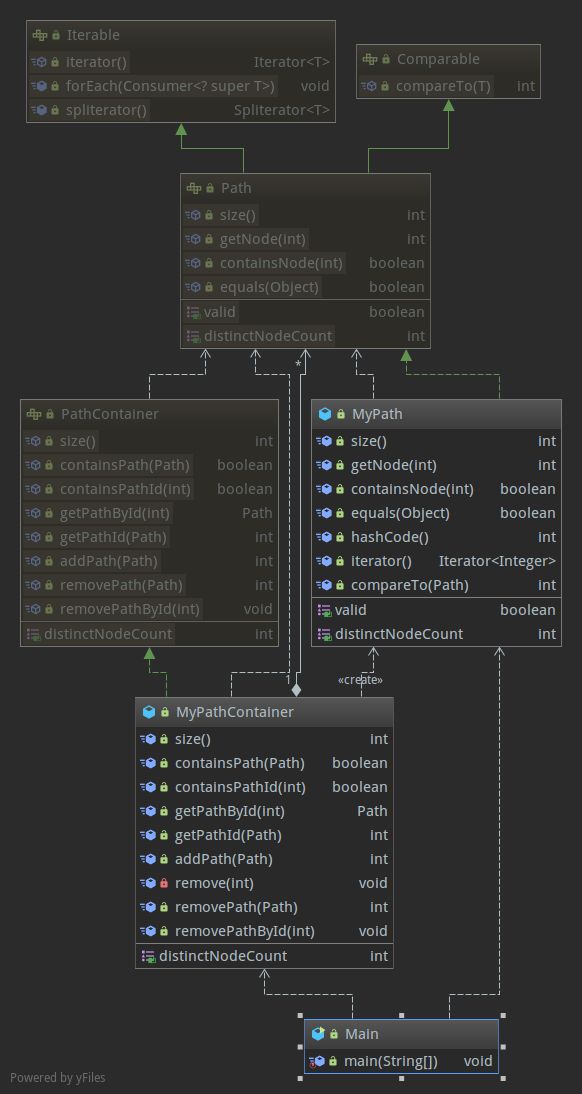
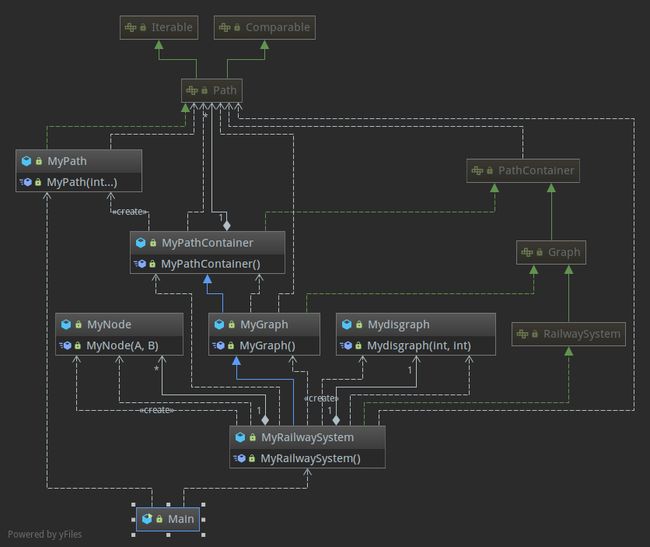
五、架构设计
这次的架构设计有助教和老师的经验在里面,我们自己设计的部分不多!老师和助教的前瞻性充分在这个单元体现出来。
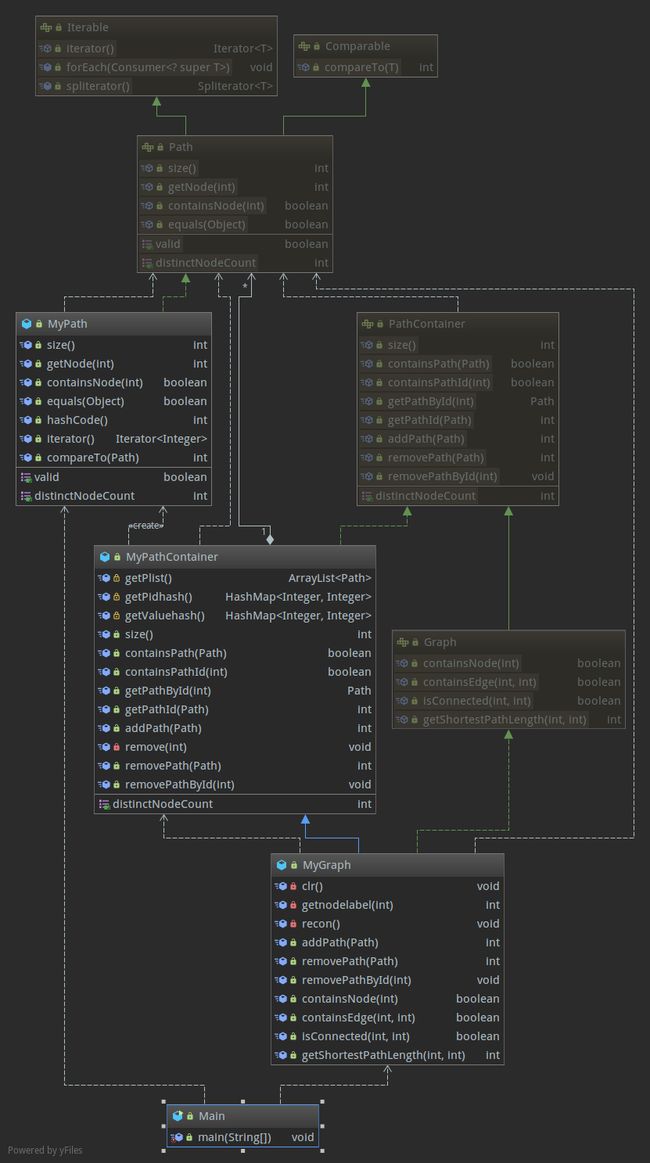
第三次,抽象出了Mydisgraph 封装出了最短路算法
用于:
- 随时调试性能
- 随时替换其他算法
- 封装共性代码
三次的架构一脉相成在架构上我改进了以前的开发策略:
- 学习相关的模式、接口设计、画流程图 (确定如何对象的属性)
- 模块绑定、避免重构
- 做头脑风暴,考察多种测试数据和思路,并完成代码
- 测试数据构造和覆盖性测试
- 代码回顾和思考
由此我实现了代码的复用和解耦。
六、debug情况
我发现了一个核心bug,滥用hashcode
有同学的第一次代码在equals方法内直接用hashcode判断,我使用了中间相遇的思路攻击了他的hash算法:
示例如下:
PATH_ADD 1 1 1
PATH_ADD 1 29792
这两条路径具有相同的hashcode。
这里其实反映了要如何使用hashcode的问题,hashcode的冲突要用equals去避免,值得同学记忆。
七、心得体会
经过这一段时间对JML规格的阅读以及上次上机时自己真正尝试写JML规格,我深深感受到了JML语言的重要性。只有使用JML语言,在进行程序编写,特别是不同人组队完成一个大型程序的编写时,才可以在最大程度上保证不同人完成在代码可以融合在一起,而不会产生各种各样奇妙的bug。
在这一单元的学习后,对前置条件,后置条件,副作用,有了比较好的理解,这是一个方法行为的核心,有了这样的规范,程序员间可以在架构层面上进行交流,也就可以在编码前期,架构设计时期进行交流,减少实现时的错误。这是我在这一单元最为印象深刻的,之后使用JML,我会在代码的注释中写明前置条件,后置条件,以及副作用,保持一个良好的习惯。
感谢OO感谢OO课程教会了我从规格层次审视代码,从更高的角度去设计去思考,做代码的主人。