语音识别概述

我的书：

淘宝购买链接
当当购买链接
京东购买链接

#语音识别概述
语音识别问题就是模式分类问题。
一个基本的语音识别系统如下图，实现是正常工作流程，虚线是训练模式分类问题中的模板（这里就是声学模型，字典和语言模型）。

图1语音识别系统组件关系图
语音识别是把语音声波转换成文字。给定目标语音的训练数据，可以训练一个识别的统计模型。用傅里叶变换将声波变换成频谱和幅度。
基于HMM的传统的声学模型依赖于语音和文本数据，以及一个单词到音素的发音字典。HMM是序列数据的生成模型。
训练后该模型将为每一个文本语句对应的备选发声波形给一个概率。这时如果给定一个说话的声波波形，则可以根据该模型找到最有可能的文本语句，但是这并不意味着找到的语句一定是正确的。
将音素以及音素序列用离散的类来模拟。语音识别的目标是预测正确的类序列。如果$z$表示从声波提取的特征向量序列，那么语音识别系统可以根据最优分类方程来工作：
KaTeX parse error: Limit controls must follow a math operator at position 31: …orname*{argmax}\̲l̲i̲m̲i̲t̲s̲_{w \in W}P(w|z…
实际上$\hat{w}$使用贝叶斯准则来计算该值。
KaTeX parse error: Limit controls must follow a math operator at position 31: …orname*{argmax}\̲l̲i̲m̲i̲t̲s̲_{w \in W}\frac…
其中$P(Z|w)$是声学似然（声学打分），代表了词$w$被说了的情况下，语音序列$Z$出现的概率。$p(w)$是语音打分，是语音序列出现的先验概率，其计算依赖于语言模型，在忽略语音序列出现概率的情况下，上式可以简化为：
KaTeX parse error: Limit controls must follow a math operator at position 31: …orname*{argmax}\̲l̲i̲m̲i̲t̲s̲_{w \in W}{P(Z|…
这样语音识别可以分为两个主要步骤，特征提取和解码。
ASR主要包括四个部分：信号处理和特征提取，声学模型（AM，acoustic model），语言模型（LM，language model）和解码搜索（hypothesis search）。

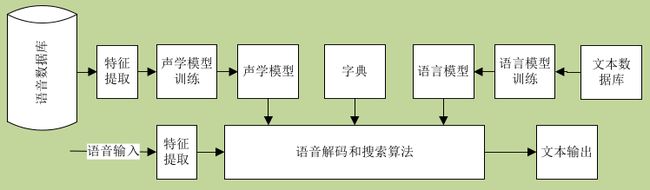
图2　连续语音识别

基于深度学习的改进如下：

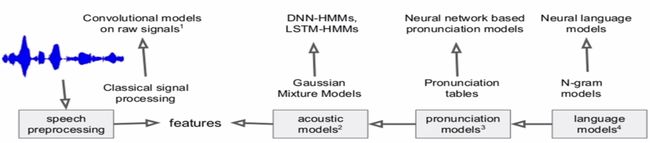
其中可以看到声学模型和语言模型是分开的，这两个部分也是分开训练的，声学模型和语言模型两者经过训练各自最优，而二组组合成的系统并不一定是最优（即系统的WER（word error rate）），这在基于深度学习领域又提出了CTC（Connectionist temporal Classification ）模型，CTC是端到端模型，即由语音特征序列直接到文字串的输出，此外，端到端模型还有LAS（Listen Attend and spell）

##语音特征提取
###用于训练的数据集

1. 经过标注的文集
2. 发音字典
3. 一些其它用于训练语音模型的数据
   ###kaldi依赖的工具
4. OpenFst 加权有限自动状态转换器（Weighted Finite State Transducer）
5. ATLAS/CLAPACK标准的线性代数库
   ###贝叶斯准则和ASR
   $$P(S|audio)=\frac{p(audio|S)P(S)}{p(audio)}$$
   其中$p$是概率密度，$P$是概率
   $S$是单词序列，$P(S)$是语言模型，如n-gram语言模型或者概率模型。$p(audio|S)$是由数据训练得到的在已经单词序列$S$时观察到发音序列$audio$的统计概率密度。语音识别时，根据给定的语音，找到单词序列$S$,其要满足$P(S|audio)$概率最大，p(audio)是一个归一化因子，可以忽略。
   ###语音特征处理
   对于语音识别系统，语音特征这里指图一中的Signal Analysis。对于麦克风采集到的信号，可以使用谱或者倒谱分析，对于ASR，常用的特征是FBANK，MFCCs以及PLP特征。
   - 特征应该包括足够的信息以区分音素（ 好的时间分辨率10ms，好的频率分辨率20~40ms)
   - 独立于基频$F_0$和其谐波
   - 对不同的说话人要有鲁棒性
   - 对噪声和通道失真要有鲁棒性
   - 具有好的模型匹配特征（特征维度尽量低，对于GMM还要求特征之间独立，对于NN方法则无此要求）
   
   预加重模块增加了高频语音信号的幅度，预加重公式如下：
   $x^{\prime }[t_d]=x[t_d]-\alpha x[t_d-1],0.95<\alpha <0.99$
   语音信号是非稳态信号，但是信号处理的算法通常认为信号是稳态的，通常加窗以获得短时平稳信号：
   $x[n]=w[n]s[n] $即$x_t[n]=w[n]x’[t_d+n]$
   为了减小截断带来的影响，通常使用hanning或者hamming窗
   $w[n]=(1-\alpha )-\alpha cos(\frac{2\pi n}{L-1})$
   
   ####麦克风采集
   对于ASR情况，采样率$f_s\le 20KHz$即有效语音频谱包含$10KHz$就足够了。为了识别率，通常有以下指标需要关注：

---

• 采样率，截止频率在8KHz，这要求采样率$f_s\ge 16KHz$，为了防止频谱混跌，通常采样率大于$16KHz$,经过重采样后到$16KHz$
• 为了减小语音失真，通常处理过程不加AGC，可以的化也不加NS（如果服务端有抗噪训练,如果不能处理噪声，ns也是需要的）
• 避免语音被截幅（AOP要高，$120dB@1KHz$），峰值电平在-20~10dBFS为宜
• 频谱尽量平坦（$\pm 3dB$,$100-8000Hz$），有两层意义，一个是麦克风频谱要求尽量频谱，一个是声音传播损耗需要预加重来增强。
• 总谐波失真要小，小于1%（从$100Hz-8KHz,@90dBSPL$）
• SNR要高（$\ge 65dB$为佳），减小ADC器件本身带来的噪声。
• 采样有效比特数，其影响的是信噪比，大于等于16bit即可
• 语音传输到服务端，对识别率由好到差（网络带宽由大到小）是：FLAC/LINEAR16， AWR_WB,OGG_OPUS

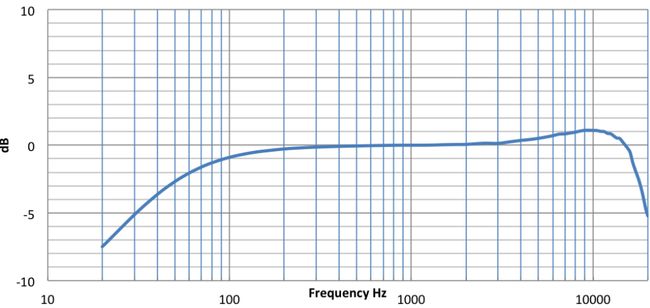
频谱平坦度实例

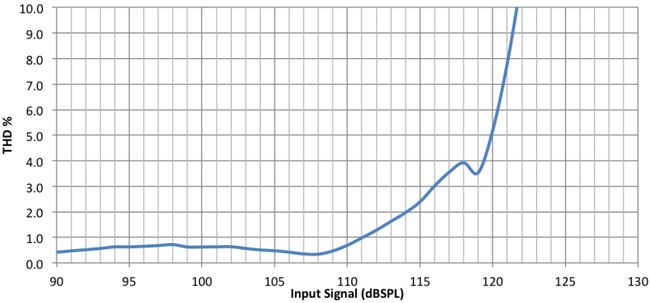
THD实例
元音的频谱共振峰特征明显。使用STFT（short time fourier specturm）将其变换到频域，这是因为声道的形状（舌头，牙齿）能用短时功率谱的包络表示出来，
一个处理的实例过程是，对输入的16khz语音，以25ms为窗大小，对窗长内数据加窗（汉宁窗）做FFT变换，对于每一个频点取对数能量，做DCT（离散余弦变换），获得导谱，取导谱的前13个系数，然后将前述25ms的窗向后滑动10ms重复上面的操作，那么每10ms将有一个向量输出。
在做DCT前，使用“梅尔”缩放对频率轴进行缩放，并不直接取DCT变换后的个频谱分量，而是采用和“梅尔”缩放一样的粒度对DCT后的频谱取三角窗平均；通常也会采取预加重技术抵消加窗带来的影响。对信号加噪。得到MFCC（Mel Frequency Ceptural Coeffs）。
此外，可选取的特征还有RASTA-PLP（相对频谱变换-感知线性预测， perceptual linear prediction）

##声学模型
声学模型使用GMM-HMM（混合高斯-隐马尔科夫模型，Gaussian mixture model-HMM），训练该模型的准则有早期的最大似然准则（ML，maximum likelihood），中期的序列判别训练法（sequence hierarchical model），以及目前广泛使用的给予deep learning的特征学习法：深度神经元网络（Deep Neural Network DNN）。
###GMM模型
用在说话人识别，语音特性降噪以及语音识别方面。
若随机变量$X$服从均值为$\mu$,，方差为$\sigma$的概率分布，则其概率密度函数是：
$$f(x)=\frac{1}{\sqrt{2\pi }}{e}^{-\frac{(x-\mu {)}^2}{2{\sigma }^2}}$$
则称$x$服从高斯分布（正态分布）。记作：
$$X\sim N(\mu ,{\sigma }^2)$$
正态随机向量$\mathbf{X}=(x_1,x_2,...,x_D{)}^T$的高斯分布是：
$$f(\mathbf{x})=\frac{1}{\sqrt[D]{2\pi }\sqrt{|\sum |}}exp[-\frac{1}{2}\frac{(\mathbf{x}-\mu {)}^T]}{\sum (\mathbf{x}-\mu )}$$
记作：$X\sim N(\mu \in R^D,\sum \in R^{D\times D})$，其中$\sum$是$D\times D$维协方差矩阵，$|\sum |$是$\sum$的行列式，$\sum =E(X-\mu )(X-\mu )$。
一个连续标量$X$的混合高斯分布的概率密度函数：
$$f(X)=\sum _{m=1}^M\frac{c_m}{\sqrt{2\pi {\sigma }_m}}{e}^{-\frac{1}{2}(\frac{x-{\mu }_m}{{\sigma }_m})}=\sum _{m=1}^M{c}_{m}N(x;{\mu }_m,{\sigma }_m^2),(-\infty <x<+\infty ;{\sigma }_m>0;c_m>0)$$
混合权重的累加和等于一，即${\sum }_{m=1}^M{c}_m=1.$和单高斯分布相比，上式是一个具有多个峰值分布（混合高斯分布），体现在Ｍ>1。混合高斯分布随机变量$x$的期望是$E(x)={\sum }_{m=1}^M{c}_m{\mu }_m$
多元混合高斯分布的联合概率密度函数是：
$$f(\mathbf{x})=\sum _{m=1}^M\frac{c_m}{\sqrt[D]{2\pi }\sqrt{|{\sum }_m|}}{e}^{-\frac{1}{2}(\mathbf{x}-{\mu }_{\mathbf{m}}{)}^T{\sum }_m^{-1}(\mathbf{x}-\mu )}=\sum _{m=1}^M{c}_{m}N(x;{\mu }_m,\sum _m),(c_m>0)$$
###参数估计
对于多元混合高斯分布，参数变量$\Theta =c_m,{\mu }_m,{\sum }_m$,这里参数估计的目标是选择合适的参数以使混合高斯模型符合建立的语音模型.
使用最大似然估计法估计混合高斯分布的参数：
$$c_m^{(j+1)}=\frac{1}{N}\sum _{t=1}^N{h}_m^{(j)}(t)$$
$${\mu }_m^{(j+1)}=\frac{{\sum }_{t=1}^N{h}_m^{(j)}(t){\mathbf{X}}^{(t)}}{{\sum }_{t=1}^N{h}_m^j(t)}$$
$$\sum _m^{(j+1)}=\frac{{\sum }_{t=1}^N{h}_m^{(j)}[{\mathbf{x}}^t-{\mu }_m^j][{\mathbf{x}}^t-{\mu }_m^j{]}^T}{{\sum }_{t=1}^N{h}_m^{(j)}(t)}$$
后验概率$h$的计算如下：
$$h_m^j(t)=\frac{c_m^{(j)}N(X^t;{\mu }_m^j,{\sum }_m^j)}{{\sum }_{i=1}^n{c}_i^{j}N({\mathbf{x}}^{\mathbf{t}};{\mu }_{\mathbf{i}}^{\mathbf{j}},{\sum }_{\mathbf{i}}^{\mathbf{j}})}$$
基于当前（第ｊ次）的参数估计，$x^t$的条件概率取决于每一个采样。
ＧＭＭ模型适合用来对语音特征建模，而现实世界中组成的字的音节所包含的语音特征是有顺序概念在里面的，这时使用ＨＭＭ来表示其次序特征。
GMM模型不能有效的对呈非线性或者近似线性的数据进行建模。
##隐马尔科夫模型HMM(hidden markov model)
HMM,的核心就是状态的概念，状态本身是离散的随机变量，用于描述随机过程。
###马尔科夫链
设马尔科夫链的状态空间是$q_t\in s^{(j)},j=1,2,...,N$，一个马尔科夫链${\mathbf{q}}_1^T=q_1,q_2,...,q_T$,可被转移概率完全表示，定义如下：
$$p(q_t=s^{(j)}|q_{t-1}=s(i))\doteq p_{ij}(t),i,j=1,2,...,N$$
如果转移概率和时间无关，则得到齐次马尔科夫链，其矩阵表示方式如下：
$$A=\left[\begin{array}{cccc}{p}_{11}& p_{12}& p_{13}& ...\\ p_{21}& p_{22}& p_{23}& ...\\ p_{31}& p_{32}& p_{33}& ...\end{array}\right],\sum p_{ij}=1$$
其观察概率分布$P(o_{t}t|s^{(i)}),i=1,2,...,N$，观察向量$o_t$是离散的，每个状态对应的概率分布用来描述观察$v_1,v_2,...,v_N$的概率：
$$b_i(k)=P(o_t=v_k|q_t=i),i=1,2,...,N$$
在语音识别中，使用HMM的概率密度函数来描述观察向量$o_t\in R^D$的概率分布，其概率密度函数在语音识别中选择GMM的概率密度函数：
$$b_i(o_t)=\sum _{m=1}^M\frac{c_{i}m}{(2\pi {)}^{D/2}|{\sum }_i{|}^{1/2}}exp[-\frac{1}{2}(o_t-{\mu }_{i,m}{)}^T\sum _{i,m}^{-1}(o_t-{\mu }_i,m)]$$
隐马尔科夫模型是统计模型，其被用来描述一个含有隐含位置参数的马尔科夫过程。其难点是从可观察的参数中确定该过程的隐含参数。然后利用这些参数来进一步的分析。例如模式识别。
###隐马尔科夫模型
其是序列的概率模型，在每一个时刻都有一个状态与之对应。计算$p(sequence|model)$包括以对指数状态序列求和。可以使用动态规划递归求解，模型参数训练的目标是最大化训练数据集的概率。
其涉及两个重要的算法

• 前向后向算法
  递归计算状态概率，在模型训练时使用。
• 维特比算法
  对于给定的字符序列，查找到最有可能的HMM状态序列。
  早期基于HMM的语言模型使用向量量化（Vector Quantization）将语音特征映射到一个符号（通常有256个符号），每一个发音由三个马尔科夫状态表示，也就是三音素模型。
  ###HMM参数学习－Baum-Welch法
  定义“完整的数据”为$\mathbf{y}=\{\mathbf{o},\mathbf{h}\}$,其中是$o$观测值(如语音特征)。$h$是隐藏随机变量（如非观测的HMM状态序列），这里要解决的是对未知模型参数$\theta$的估计，这通过最大化对数似然度$logp(o|\theta )可以求得$，然而直接求解不易。可转换为如下公式求$\theta$的估计：
  $$Q(\theta |{\theta }_0)=E_{h|o}[\log p(\mathbf{y};\theta )|\mathbf{o};{\theta }_0]=E[\log p(\mathbf{o},\mathbf{h};\theta )|\mathbf{o};{\theta }_0]$$
  其中${\theta }_0$是前一次的估计。则上式离散情况下的期望值如下：
  $$Q(\theta |thet{a}_0)=\sum _{h}p(\mathbf{h}|\mathbf{o})\log p(\mathbf{y}:\theta )$$
  为了计算的方便，将数据集改为$$\mathbf{y}=[{\mathbf{o}}_1^T,{\mathbf{q}}_1^T]$$,$\mathbf{o}依然是观测序列$，$\mathbf{h}是观测序列$，$mathbfq$是马尔科夫链状态序列，BaTum-Welch算法中需要在Ｅ步骤中计算得到如下的条件期望值，或成为辅助函数$Q(\theta |{\theta }_0)$:
  $$Q(\theta |{\theta }_0)=E[\log p({\mathbf{o}}_1^{\mathbf{T}},{\mathbf{q}}_1^{\mathbf{T}}|\theta ){\mathbf{o}}_1^{\mathbf{T}},{\theta }_0]$$
  这里期望通过隐藏状态序列${\mathbf{q}}_1^{\mathbf{T}}$确定得到。
  ###维特比算法
  在给定观察序列${\mathbf{o}}_1^T={\mathbf{o}}_1,{\mathbf{o}}_2,...,{\mathbf{o}}_T$的情况下，如何高效的找到最优的HMM状态序列。动态规划算法用于解决这类$\mathbf{T}$阶路劲最优化的问题被称为维特比（Viterbi）算法。对于转移状态$a_{ij}$给定的HMM，设状态输出概率分布为$b_i({\mathbf{o}}_{\mathbf{t}})$，令${\delta }_i(t)$表示部分观察序列${\mathbf{o}}_1^t$到达时间$t$，同时相应的HMM状态序列在该时间处在状态$i$时的联合似然度的最大值：
  $${\delta }_i(t)=ma{x}_{q_1,q_2,...,q_{t-1}}P({\mathbf{o}}_1^t,q_1^{t-1},q_t=i)$$
  对于最终阶段$t=T$，有最优函数${\delta }_i^T$，这通过计算所有$t\le T-1$的阶段来得到。当前处理$t+1$阶段的局部最优似然度，可以使用下面的函数等式来进行递归得到：
  $${\delta }_j^{t=1}=ma{x}_i{\delta }_i(t)a_{ij}{b}_j({\mathbf{o}}_{t+1})$$
  在语音建模和相关语音识别应用中一个最有趣且特别的问题就是声学特征序列的长度可变性。
  ###HMM识别器
  单词序列$\mathbf{W}(w_1,w_2,...,w_k)$被分解为基音序列。在已知单词序列$\mathbf{W}$下观察到特征序列$\mathbf{Y}$的概率$p(\mathbf{Y}|\mathbf{W})$按如下公式计算：
  $$P(Y|W)=\sum _{Q}P(y|Q)P(Q|W)$$
  $\mathbf{Q}$是单词发音序列$Q_1,...,Q_k$，每一个序列有事基音的序列$Q_k=q_1^{(k)},q_2^{(}k)...,$,则有：
  $P(Q|W)={\prod }_{k=1}^{K}P(Q_k|w_k)$
  
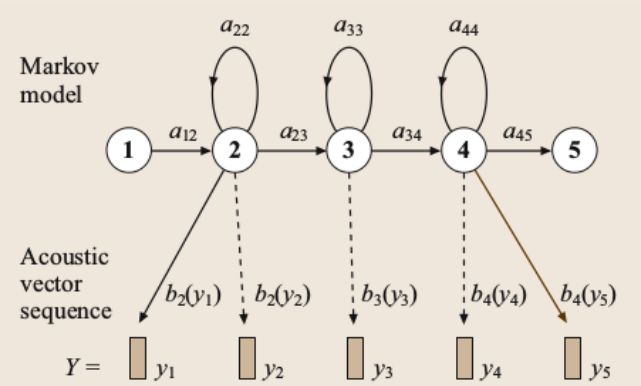
  图2 基于HMM的音素模型
  如上图所示，基音$q$由隐马尔科夫密度表示，状态转移参数是$a_{ij}$,观察分布是{b_j()}，其通常是混合高斯分布：
  $b_j(\mathbf{y})={\sum }_{m=1}^M{c}_{jm}N(\mathbf{y};{\mu }_{jm},{\sum }_{jm})$
  其中$N$是均值为${\mu }_{jm}$,方差为${\sum }_{jm}$,约10到20维的联合高斯分布。由于声学向量$\mathbf{y}$维度较高，协方差矩阵通常限制为对角阵。状态进入和退出是非发散。$\mathbf{Q}$是基音序列的线性组合，声学似然如下：
  $p(\mathbf{Y}|\mathbf{Q})={\sum }_{X}p(\mathbf{X},\mathbf{Y}|\mathbf{Q})$
  其中$\mathbf{X}=x(0),...,x(T)$是混合模型的状态序列。
  $$p(\mathbf{X},\mathbf{Y}|\mathbf{Q})=a_{x(0),x(1)}\prod _{t=1}^T{b}_x(t)(y_t)a_{x(t),x(t+1)}$$
  声学模型参数$a_{ij}$和$b_j()$可以使用期望最大化的方式从语料库中训练得到。
  由于发音通常是上下文相关的，如food和cool，通常使用三音子模型，以实现上下文相关法。如果有N个基音。那么将有$N^3$个可能的三音子。可以使用映射集群的方式缩减规模。
  逻辑到物理模型集群通常是对状态层次的集聚而非模型层级的集群，每个状态所属的集群通过决策树确定。每个音素$q$的状态位置有一个二进制决策树与之相关。每一个音素模型有三个状态，树的每个节点都是语义的判断。将由$q$得到的逻辑模型音素$q$的状态$i$的集群。以最大化训练数据集的最终状态集概率为准则设置各个节点的判断条件。

##语言模型
语言模型计算单词序列的概率$p(w_1,w_2,...,w_3)$,传统语言模型当前词的概率依赖前n个单词，这通常由马尔科夫过程描述。
$$p(w_1,...,w_m)=\prod _{i=1}^{m}p(w_i|w_1,...,w_{i-1})\approx \prod _{i=1}^{m}p(w_i|w_{i-(n-1)},...,w_{i-1})$$
###N-gram语言模型
一个单词序列$W=w_1,...,w_k$的概率由以下公式表示：
$p(W)={\prod }_{k=1}^{K}p(w_k|w_{k-1},...,w_1)$
对于大词汇量的识别问题，第$N$个单词的概率只依赖于前$N-1$个。
$$p(W)=\prod _{k=1}^{K}p(w_k|w_{k-1},w_{k-2},...,w_{k-N+1})$$
通常N取2~4。通过计算训练数据集中N-gram出现的次数来形成最大似然概率。例如：
$C(w_{k-2}{w}_{k-1}{w}_k)$是$w_{k-2}{w}_{k-1}{w}_k$三个词出现的次数，$C(w_{k-2}{w}_{k-1})$是$w_{k-2}{w}_{k-1}$出现的概率，则：
$p(w_k|w_{k-1}{w}_{k-2})\approx \frac{C(w_{k-2}{w}_{k-1}{w}_k)}{C(w_{k-2}{w}_{k-1})}$
这种统计方式存在一个数据稀疏性问题。这通过结合非技术概率模型解决。
$p(w_k|w_{k-1},w_{k-2})=\frac{C(w_{k-2}{w}_{k-1}{w}_k)}{C(w_{k-2}wk-1)}$
一元和二元语法模型的概率基于训练文集中单词出现的次数来统计。
$$p(w_2|w_1)=\frac{count(w_1,w_2)}{count(w_1)}$$
$$p(w_3|w_1,w_2)=\frac{count(w_1,w_2,w_3)}{count(w_1,w_2)}，如果c>c^{\prime };=d\frac{count(w_1,w_2,w_3)}{count(w_1,w_2)}，如果0<C<C^{\prime };=\alpha (w_{k-1,w_{k-2}})p(w_k|w_{k-1})，其它$$
其中$C$是计数门限，$d$是不连续系数，$\alpha$是归一化常数。
如果语音模型完全符合HMM模型（基于对角协方差多元高斯混合分布概率模型）假设的统计特性病切训练数据是充足的，那么就最小方差和零偏场景，最大似然准则解是最优解。可以从两个方面弥补非理想性，一个是参数估计策略，一个是模型。也有很多方法从这两个方面提升性能。
###归一化
归一化的目的是减小环境和说话人物理特性差异的影响。由于前端特征源于对数频谱，特征值均值归一化见笑了通道的差异影响。倒谱方差归一化缩放每一个特征系数以获得单位方差，这减小了加性噪声的影响。
声道长度变化将导致共振峰频率近似线性变换，所以在前端特征提取时考虑线性缩放滤波器中心频率以获得近乎一致的共振峰频率，这一过程被称为VTLN(vocal-track-length normalization)。VTLN需要解决缩放函数定义和针对每个说话人的缩放函数参数估计。缩放函数可以采用分段线性函数（针对男声和女声所含信息不同）。
另外，如果训练语音数据集不能完全覆盖测试集中的说话人和说话场景，则语音识别将会产生错误，这类问题可以通过自适应的方法进行求解。
##加权有限状态转换机的语音识别
这是传统的语音识别方法，包括HMM模型，文本相关模型，发音字典，统计语法，单词和音素格。

图3 传统ASR流程
###加权有限自动机
有限自动机定义为一个五元组：
$A=(Q,\sum ,E,q_0,F)$
其中$Q$是状态集合，$\sum$是输入符号集合，$E$为转移（边）集，其接收一个状态和输入符号，输出一个目的状态或者空。$q_0\in Q$是初始状态，$F\subset Q$是最终状态集或者接受状态集。
###权值的半环理论
语音识别时，不仅仅想要知道某个字串是否能够被接受，还要知道字串在语音中出现的概率。一个半环为一个五元组：

##DNN（Deep neutral network）深度神经网络
2013年算是语音识别新高度的又一个重要年份，该年提出基于深度学习的方法获得的效果比传统的好，不需要进行声学和语言进行建模，且自动学习过程可以获得比传统高斯等模型获得更加准确的毕竟（前提条件是训练模型的数据要准）。

名字起的很霸气，神经网络，实际上和生物神经相比还差十万八千里的距离，这里的DNN实际上就是计算图，更具体的多就是矩阵运算再加上非线性计算。
不过这里依然沿用媒体上的流行说法“神经元”。
2013~205
由于语音的前后相关性，所以多用RNN的方式进行处理，但是villa DNN（经典）由于其训练难度大等特性，其不同的变种RNN（区别于CNN）被各类学者提出来，这些模型包括LSTM/GRU，以及它们的很多其它的变种，这带来的好处是，计算量大大减小，很快称为新一代工程实现的首选。
这期间为了提升性能，也有其它额外的组件出来，如attention方法，行卷积方法等等
2016～
由于之前的声学模型和语言模型是分开训练的，它们的判决准则并不一致，所以会有一些拟合的方法加以改进这种不足，不过以前的方法多是修修补补，这个时段提出“端到端”的思想，举例来说，输入和传统语音识别系统一样，可以是MFCC或者PLP等特征，中间模块不再区分声学模型还是语言模型，一步到位，输出可以是音素，字符或者单词，这种模型的好处是对训练数据集不再要求是按照音素对齐的（loss函数是基于对其的方式求得的），可以丢弃掉音素的概念，这里的损失函数。基本思想是对于给定的输入序列，将网络输出理解成所有可能label的一个概率分布。经过分类后可以得到一个label。CTC就是端到端用的非常广的一种方法。

这期间还有将CNN和RNN拼接起来获得更高性能的，还有使用深度学习方法处理前端语音增强的。

###深度神经元网络架构
深度神经元网络是传统的多层感知系统（MLP，multilayer perception）。
${\mathbf{V}}^l=f(z^l)=f({\mathbf{W}}^l{\mathbf{v}}^l+{\mathbf{b}}^l),0<l<L$
此处，$z^l={\mathbf{W}}^l{\mathbf{v}}^l+{\mathbf{b}}^l\in R^{N_1\times l},{\mathbf{v}}^l\in R^{N_1\times l},{\mathbf{W}}^l\in R^{N_l\times 1},N_l\in R$他们分别是激励向量，权重矩阵，偏移向量以及$l$层神经元数。${\mathbf{v}}^0=0\in R^{N_0\times l}$是观测（特征）向量。$N_0=D$是特征维度。$f(\cdot )$是激励函数。
###训练评价准则
最小期望准则：
$J_{EL}=E(J(\mathbf{W},\mathbf{b};\mathbf{o},\mathbf{y}))={\int }_{o}J(\mathbf{W},\mathbf{b};\mathbf{o},\mathbf{y})p(o)d(o)$
$\{\mathbf{w},\mathbf{b}\}$是参数模型，$\mathbf{o}$是观测向量，$y$是输出向量，$p(o)$是观测向量$o$概率密度函数，$J(\mathbf{W},\mathbf{b};\mathbf{o},\mathbf{y})$是损耗函数。
回归问题常采用均方误差准则：
$J_{MSE}mathbf(W,b;S)=\frac{1}{M}{\sum }_{m=1}^M{J}_{MSE}(\mathbf{W},\mathbf{b};{\mathbf{o}}^{\mathbf{m}},{\mathbf{y}}^{\mathbf{m}})$
$J_{MSE}mathbf(W,b;o,y)=\frac{1}{2}||{\mathbf{v}}^{\mathbf{L}}-\mathbf{y}|{|}^2$
对于分类问题，y是概率分布，则使用交叉熵准则：
$J_{CE}=(\mathbf{W},\mathbf{b};\mathbf{S})=\frac{1}{M}{J}_{CE}((\mathbf{W},\mathbf{b};{\mathbf{o}}^{\mathbf{m}},{\mathbf{y}}^{\mathbf{m}}))$
###数据预处理
在语音识别中，CMN（Cepstral Normalization）导谱系数归一化，即减去每个音节MFCC特征的均值能减小通道引入的畸变。CMN的归一化可以通过首先估算样本的均值，然后用样本值减去估算均值而得到。

DNN-HMM混合系统架构

###SyntaxNet
谷歌2016开源，称“世界最准确解析器”，tensorflow框架下快速，高性能的句法分析器。有三个特色

• 无标注数据-Tri-training
• 调整过的神经网络模型
• 结构感知
  ###Word2vec&Glove
  word2verc是谷歌2013年开源的词向量处理法，占用内存少，glove是全局向量的缩写，也是谷歌开源词向量技术，数据量充足时训练效果会优于word2vec，训练时间长。
  ####Skip-Gram模型
  每一个字$w\in W$由一个向量表示$v_w\in R^d$，类似的每一个上下文$c\in C$由向量$v_c\in R^d$表示， $W$是单词，$C$是上下文,$d$是嵌入的维度。
  该语法模型的目的是查找使单词-上下文对最为合理的$v_w\cdot v_c$乘积。
  假设观察到的单词$w$和上下文$c$对$(w,c)$的数据集是$D$.
  使用$p(D=1|w,c)$指示$(w,c)$源于数据集$D$的概率。$p(D=0|w,c)=1-p(D=1|w,c)$表示$(w,c)$不在数据集$D$的概率。分布模型如下：
  $$p(D=1|w,c)=\frac{1}{1+e^{-v_w\cdot v_c}}$$
  其中$v_w$和$v_c$是两个要学习的$d$维向量。目标是使观察到的单词/语句对的对数概率最大化，这样可以得到目标函数：
  $$argma{x}_{v_w,v_c}\sum _{(w,c)\in D}log\frac{1}{1+e^{-v_c\cdot v_w}}$$