如何理解FFT
我的书:
![]()
淘宝购买链接
当当购买链接
京东购买链接
时域信号分为周期/非周期,连续和离散,这样有四中样式的傅里叶变换。
| 变换类型 | 时域信号特性 | 频谱特性 |
|---|---|---|
| 连续时域FT | 连续,非周期 | 非周期,连续 |
| 离散时域傅里叶变换DTFT | 离散非周期 | 周期,连续 |
| 傅里叶级数FS | 连续,周期 | 非周期,离散 |
| 离散傅里叶变换DFT | 离散,周期 | 周期,离散 |
如上可以看到,在一个域的离散信号,在另一个域将变成周期的,类似的,在一个域连续的信号,在另外一个域必然是非周期的。
###DFT
分为实数和复数版本的DFT,实数版本输入是实数,得到的频域点将有两个集合,分别是 cos \cos cos和 sin \sin sin函数的系数。复数输入表示的是正负频率。
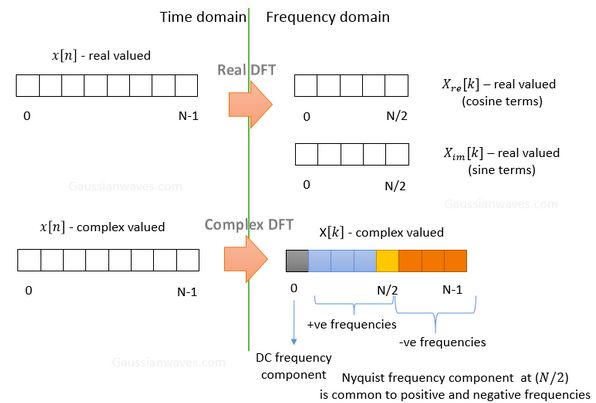
####实 DFT
对于输入是 x ( n ) x(n) x(n)的N点DFT将获得 N / 2 + 1 N/2+1 N/2+1的两组 cos \cos cos和 sin \sin sin系数
X r e [ k ] = 2 N ∑ n = 0 N − 1 x [ n ] cos ( 2 π k n N ) , K = 0 , 1 , . . , N / 2 X_{re}[k]=\frac{2}{N}\sum \limits_{n=0}^{N-1}x[n]\cos(\frac{2\pi kn}{N}),K=0,1,..,N/2 Xre[k]=N2n=0∑N−1x[n]cos(N2πkn),K=0,1,..,N/2
X i m [ k ] = 2 N ∑ n = 0 N − 1 x [ n ] sin ( 2 π k n N ) , K = 0 , 1 , . . , N / 2 X_{im}[k]=\frac{2}{N}\sum \limits_{n=0}^{N-1}x[n]\sin(\frac{2\pi kn}{N}),K=0,1,..,N/2 Xim[k]=N2n=0∑N−1x[n]sin(N2πkn),K=0,1,..,N/2
根据系数获取原始输入时,需要对 X r e [ 0 ] X_{re}[0] Xre[0]和 X r e [ N / 2 ] X_{re}[N/2] Xre[N/2]除以2。
###复DFT
对于N点复数DFT变换后得到的是N点 X [ k ] X[k] X[k]。
X [ k ] = 1 N ∑ n = 0 N − 1 x [ n ] e − j 2 π k n / N X[k]=\frac{1}{N}\sum \limits_{n=0}^{N-1}x[n]e^{-j2\pi kn/N} X[k]=N1n=0∑N−1x[n]e−j2πkn/N
变换后的 X [ 0 ] X[0] X[0]是直流分量, 1 ∼ N / 2 1\sim N/2 1∼N/2是正频成分, X [ N / 2 ] X[N/2] X[N/2]是奈奎斯特频率,接下来的 N / 2 − 1 N/2-1 N/2−1是负频分量。
从频谱获得原始输入信号的公式是:
x [ n ] = ∑ k = 0 N − 1 X [ k ] e j 2 π k n / N x[n]=\sum \limits_{k=0}^{N-1}X[k]e^{j2\pi kn/N} x[n]=k=0∑N−1X[k]ej2πkn/N
当时域信号是实数时,计算复DFT时,将虚部填零,下图是matlab fft函数计算的DFT结果。
##FFT
FFT是DFT计算的快速方法。
X [ k ] = ∑ n = 0 N − 1 x [ n ] e − j 2 π k n / N X[k]=\sum \limits_{n=0}^{N-1}x[n]e^{-j2\pi kn/N} X[k]=n=0∑N−1x[n]e−j2πkn/N
x [ n ] = 1 N ∑ k = 0 N − 1 X [ k ] e j 2 π k n / N x[n]=\frac{1}{N}\sum \limits_{k=0}^{N-1}X[k]e^{j2\pi kn/N} x[n]=N1k=0∑N−1X[k]ej2πkn/N
matlab
x=fft(x,N),%计算X[k]
x=ifft(x,N)
###FFT结果举例
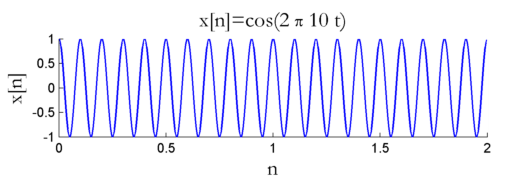
假设 x [ n ] x[n] x[n]是频率 f c = 10 H z f_c=10Hz fc=10Hz余弦信号,采样率是 f s = 32 ∗ f c f_s=32*f_c fs=32∗fc
fc=10;
fs=32*fc;%sampling frequency with oversampling factor=32
t=0:1/fs:2-1/fs;%2 seconds duration
x=cos(2*pi*fc*t);%time domain signal (real number)
subplot(3,1,1); plot(t,x);hold on; %plot the signal
title('x[n]=cos(2 \pi 10 t)'); xlabel('n'); ylabel('x[n]');
X = fft(x,N);%N-point complex DFT
%output contains DC at index 1, Nyquist frequency at N/2+1 th index
%positive frequencies from index 2 to N/2
%negative frequencies from index N/2+1 to N
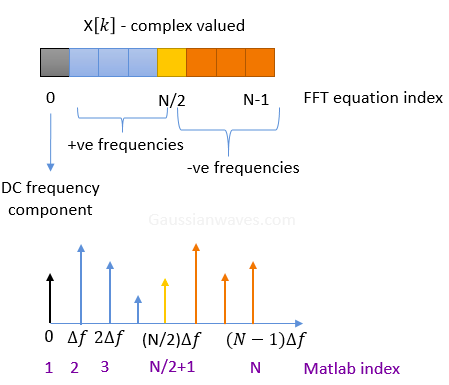
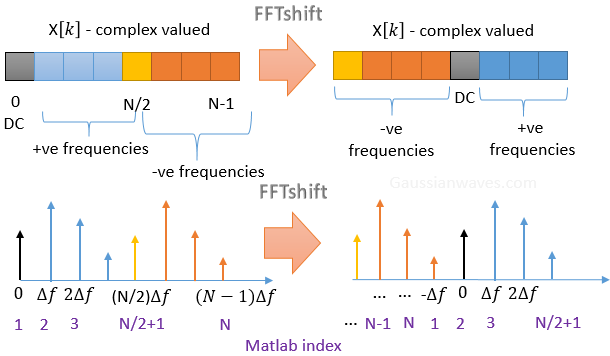
matlab数组从1开始,输出1-N,频点间隔是 Δ f = f s N \Delta f=\frac{f_s}{N} Δf=Nfs,先输出直流分量,然后是正频分量,再然后是负频分量,在MATLAB中使用fftshift后将频率按,负频分量,直流以及正频分量排列。
##实信号

1)实数信号以 f s f_s fs为采样率,那奎斯特采样定理表明混跌频率是 f s / 2 f_s/2 fs/2,则
2)实数信号的fft结果中前半部分是 [ 0 , f s / 2 ] [0,f_s/2] [0,fs/2],后半部分是 [ f s / 2 , f s ] [f_s/2,f_s] [fs/2,fs]由于周期性,在频谱不混跌的情况下,后半部分等于 [ − f s / 2 , 0 ] [-f_s/2,0] [−fs/2,0],在上图中看到第一个数是 36 + 0 i 36+0i 36+0i,这就是直流分量,
3)另外还应该注意到第i个数,实际上等于第 N − i N-i N−i个数的共轭,
4)所以实际上实数的快速傅里叶算法会利用这个性质减小运算量和存储空间,这是在代码级别的优化
5)在实际频率显示时,某些场合期望得到 [ − f s / 2 , f s / 2 ] [-f_s/2,f_s/2] [−fs/2,fs/2]显示频谱,通常会使用matlab 的fftshift来实现这个功能。
##复信号
1)对于复信号没有负频率,以 f s f_s fs采样率的信号,fft频谱的结果是从 [ 0 , f s ] [0,f_s] [0,fs];
2)在 f > f s / 2 f>f_s/2 f>fs/2时,对复信号的fft结果进行fftshift会产生频谱混跌。