谷歌面试10道编程题及答案（MIT版） | 面试笔记

目录

问题 1：硬币难题

问题 2：在数组中进行查找

问题 3：A to I（字符串转换为整数）

问题 4：颠倒字符串中的单词顺序

问题 5：最近邻

问题 6：洗牌问题

问题 7：单链表中的循环

问题 8：计算 2^x

问题 9：二叉搜索树

问题 10：排除 bug

---

问题 1：硬币难题

假设你有 8 枚大小相同的硬币，但其中 1 枚硬币要比其他 7 枚稍重一点（但你不知道具体是哪一枚）。同时，你还有一个老式天平可以称重，从而得出哪枚硬币稍重（或是否重量相同）。那么，最少要称多少次才能找出那枚稍轻的硬币？

优秀答案：最少要称两次。方法是从 8 枚硬币中取出 6 枚，天平左右盘各放 3 枚。结果会出现两种情况：

1. 两边重量不相等。

1）左盘 3 枚硬币重，则较重的 1 枚在左盘；（右盘重的情况也一样）

2）再从3枚硬币中任取两个进行称重，若重量相等则剩下的1枚为最重的硬币；若重量不等，则再次称重这两枚硬币即可。

2. 两边重量相等。

1）天平左右盘的6枚硬币重量相等，则称剩下的 2 枚硬币，得到稍重的这枚硬币。

不太好的答案：分别取 4 枚硬币放置于天平左右盘，找出较轻的一组（4 枚），将该组硬币继续分为两组放入天平左右盘，找出较轻的一组（2 枚），再次重复此步骤找到最轻的一枚。（这种方法可能需要3次）

 

问题 2：在数组中进行查找

给定一个已排序的整数数组，如何找出特定整数 x 的位置？

优秀答案：使用二分搜索法。将数组中间的数字与 x 进行比较。如果相同，则找出了 x。如果数组中的数字较大，则需要查看数组后半部分。如果数字较小，则需要查看数组前半部分。通过比较数组中间元素和 x，我们可以重复搜索该数组的前后部分，从而再次将搜索范围缩小 2 倍。我们重复这一过程直至找出 x。这种算法花费的时间为 O(log n)。

不太好的答案：按顺序查看数组的每个数字，与 x 进行比较。这种算法花费的时间为 O(n)。

 

问题 3：A to I（字符串转换为整数）

编写一个函数将字符串转换为整数（这个函数被称为 A to I 或者 atoi()），因为我们要将一个 ASCII 字符串转换为整数。

（剑指offer有原题，还未刷到~）

优秀答案：从头到尾查看整个字符串。如果首个字符为负号，记下来。从 0 开始进行累计求和。每得到一个新数字，总数乘以 10 并加上这个新数字。当计算结束时，返回当前总数，或者如果出现负号，返回该数字的倒数。

凑合的答案：另一种方法也是从头到尾查看整个字符串，再次进行累计求和。记住表示当前你所在数字的数字 x，x 最开始为 1。针对每个字符，将当前数字乘以 x 并添加到累计总数中，同时将 x 乘以 10。当你到达字符串起点时，返回当前总数，或者如果出现负号，返回该数字的倒数。

注意：面试官可能会询问你自身方法的局限性。你应该回答：只有字符串在每个数字前都包含可选负号时，该方法才能生效。同时，你还应提到：如果数字太大，则结果会因为溢值原因而不正确。

 

问题 4：颠倒字符串中的单词顺序

编写一个函数将字符串中的单词顺序进行颠倒。

答案：

1）交换第一个与倒数第一个、第二个与倒数第二个字符的顺序，以此类推，颠倒整个字符串。

2）之后，查看整个字符串，找出空格，这样就可以发现每个单词的位置。再次交换第一个与倒数第一个、第二个与倒数第二个单词的顺序，以此类推，颠倒你所遇到的每个单词的顺序。

 

问题 5：最近邻

假设你有一个包含 n 个人信息的数组。每个人分别用一个字符串（他们的名字）和一个数字（他们在数轴上的位置）表示。每个人有三个朋友，即数字和他本人最接近的三个人。请写出一个可以找出每个人的三个朋友的算法。

优秀答案：按每个人数字的升序对数组进行排列。查看每个人前后紧邻的三个人，他们的朋友将出现在这六个人当中。这一算法花费的时间为 O(n log n)，因为将人进行分类也会花费那么多时间。

 

问题 6：洗牌问题

给定一组不同的整数数组，给出一个算法对这些整数进行随机排序，使每个重排序方法的可能性相等。换句话说，给定一副牌，你要如何洗牌才能确保牌的每种排列方法有相同的可能？

优秀答案：按顺序排列这些元素，用数组中不先于某个元素出现的随机元素与该元素进行交换。需要的时间为O(n)。

注意：这个问题有多个可能的答案，也有几种看似不错但实际上并不正确的答案。例如，对上面的算法做一个小小的修改，即，将每个元素与数组中的任意一个元素交换并不能确保每种重排顺序等概率出现。这里给出的答案（在作者看来）是最佳答案。如果想了解其他答案，可以在维基百科上搜一下「Shuffling」。

 

问题 7：单链表中的循环

如何确定单链表是否有循环？

优秀答案：跟踪链表中的两个指针，并在链表的开始处启动它们。在算法的每轮迭代中，将第一个指针往前移一个节点，把第二个指针往前移两个节点。如果两个指针始终相同（不是在算法起点处），那么就有一个循环。如果指针在两个指针相同之前就达到链表的末端，链表中就没有循环。其实，指针不需要一次移动一到两个节点；指针也不需要以不同的速率移动。这个过程需要的时间为 O(n)。这是一个巧妙的回答，面试官会莫名喜欢。（不太明白这是什么意思~）

凑合的回答 1：对于你在逐一浏览链表时遇到的每个节点，将指向该节点的指针放入 O(1) 中——查找时间数据结构，如散列集。接下来，当你遇到一个新的节点时，要看看指向那个节点的指针是否已经存在于你的散列集中。这一过程花费的时间为 O(n)，但占用的空间也是 O(n)。

凑合的回答 2：浏览链表中的元素，「Mark」你到达的每个节点。如果在抵达末端之前你到达了一个 mark 过的节点，列表中就有循环，否则就没有循环。这一过程花费的时间也是 O(n)。

注意：这个问题在技术上是不恰当的。一个普通的链表不会有循环。他们的意思是让你决定能否从一个图中的节点到达循环，该图包含最多有一条输出边的节点。

 

问题 8：计算 2^x

如何快速计算 2^x？

优秀答案：1 << x

通过2进制里的位移来实现，把1往左移x位。

 

问题 9：二叉搜索树

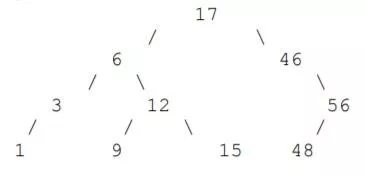
二叉搜索树是一种排序保存项目的数据结构，它由二叉树组成。每个节点都有一个指向两个子节点的指针（可能为 null），一个指向其父节点的可选指针（也可以为 null），以及一个存储在树中的元素（可能是一个字符串或一个整数）。要使二叉搜索树有效，每个节点的元素必须大于其左子树中的每个元素，并且小于其右子树中的每个元素。例如，二叉树可能如下所示：

要检查元素是否出现在二叉搜索树中，只需要遵循父对子之间的相应连接。例如，如果我们想在上面的树中搜索 15，我们从最上方的 17 开始。由于 15<17，我们移动到左边的节点 6。由于 15> 6，我们移动到右边的节点 12；由于 15>12，我们再次移动到正确的节点 15，最终找到了需要的数字。

要将元素加入二叉搜索树，我们就要像搜索元素一样，遵循从父节点到子节点的正确连接。当所需的子项为 null 时，我们将该元素添加为新的子节点。例如，如果我们要在上面的树中添加 14，我们就需要不断往下寻找添加的位置。当我们到达 15，就会看到该节点没有左子节点，因此我们将 14 添加为左子节点。

要从二叉搜索树中删除一个元素，我们首先要找出包含该元素的节点。如果该节点没有子节点，直接删除即可。如果该节点有一个子节点，则用这个子节点替代它。如果该节点有两个子节点，我们通过一种算法确定树中下一个更小或下一个更大的元素。为简单起见，这里就不赘述所使用的算法了。我们将节点中存储的元素设定为该值。之后，我们从树中拼接包含该值的节点。这个过程相对较容易，因为节点最多有一个子节点。例如，为了从树中删除 6，我们首先将节点值更改为 3。之后，我们删除原本值为 3 的节点，并将原本值为 6 的节点的左子节点值设定为 1。

在二叉搜索树上做小小的修改，就可以使用它将键与值关联起来，就像在散列表中一样。我们不需要在每个节点上存储单个值，而是存储一个键值对。该树将根据节点的键进行排序。

面试官有时会问到二叉搜索树的问题。此外，二叉搜索树往往在回答面试问题时也很有用。需要记住的重要一点是，插入、删除和查找需要的时间为 O(log n)，其中 n 是树中的元素数量，因为一个平衡良好的二叉搜索树的高度是 O(log n)。尽管在最糟糕的情况下，一个二叉搜索树的高度可能为 O(n)，「自平衡」二叉搜索树可以周期性地重组一个 BST 来确保其高度为 O(log n)。许多自平衡 BST 保证这些操作花费的时间为 O(log n)。

 

问题 10：排除 bug

描述一种从程序中找出 bug 的方法。

答案：这个问题有多个可能的答案，也是面试官经常会问的开放性问题。优秀答案可能包括：根据程序的行为判断可能出现 bug 的部分；使用断点和 stepper 逐步执行程序。任何试图找到 bug 源头和缩小 bug 搜索范围的方法都是好答案。

 

想要了解更多问题和答案可以点击：http://courses.csail.mit.edu/iap/interview/materials.php