粒子群算法
一、解决最优化问题的方法:
1》传统搜索方法:保证能找到最优解
2》启发式搜索:不能保证找到最优解
二、定义
粒子群优化算法(Particle Swarm Optimization,PSO)是自然计算的一个分支,是一种模拟自然界的生物活动的随机搜索算法。
群体迭代,粒子在解空间追随最优的粒子进行搜索。
三、基本原理:
基础:信息的社会共享
四、算法描述:
1》鸟群:假设一个区域,所有的鸟都不知道食物的位置,但是它们知道当前位置离食物还有多远。
2》算法本质:每个解看作一只鸟,称为“粒子(Particle)”,所有的粒子都有一个适应值,每个粒子都有一个速度决定它们的飞翔方向和距离,粒子们追随当前最优粒子在解空间中搜索。
3》PSO算法:初始化为一群随机粒子,通过迭代找到最优。每次迭代中,粒子通过跟踪“个体极值(pbest)”和“全局极值(gbest)”
来更新自己的速度和位置。
3.1》 pbest:每一个个体在它移动或搜索过程中记录的最优的值。
3.2》gbest:整个群体在所有的搜索过程中,找到的最佳的值。
总结:
口每个寻优的问题解都被想像成一只鸟,称为“粒子”。所有粒子都在一个D维空间进行搜索。
口所有的粒子都由一个fitness function确定适应值以判断目前的位置好坏。
口每一个粒子必须赋予记忆功能,能记住所搜寻到的最佳位置。
口每一个粒子还有一个速度以决定飞行的距离和方向。这个速度根据它本身的飞行经验以及同伴的飞行经验进行动态调整。
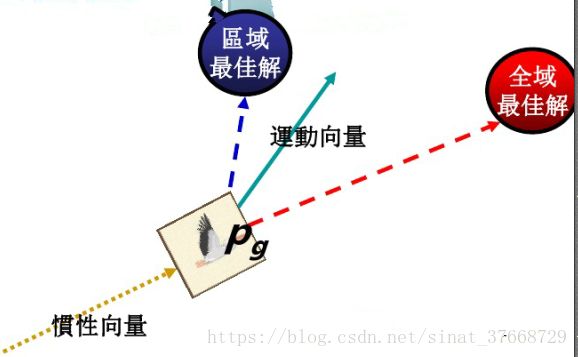
4》粒子速度和位置的更新(单位时间):
口粒子速度更新公式包含三部分:
第一部分为粒子先前的速度
第二部分为“认知”部分,表示粒子本身的思考,可理解为粒子当前位置与自己最好位置之间的距离。
第三部分为“社会”部分,表示粒子间的信息共享与合作,可理解为粒子i当前位置与群体最好位置之间的距离品。
五、参数设置:
1》群体大小-m
m是一个整型参数.
m很小:陷入局优的可能性很大。
m很大:PSO的优化能力很好,当群体数目增长至一定水平时,再增长将不再有显著的作用。
2》权重因子:
惯性因子 :ω
ω=1:基本粒子群算法。
ω=0:失去对粒子本身的速度的记忆。
学习因子:c1、c2
C1 = 0,无私型粒子群算法,“只有社会,没有自我”但是易迅速丧失群体多样性,易陷于局优而无法跳出
C2 = 0,自我认知型粒子群算法,“只有自我,没有社会”,完全没有信息的社会共享导致算法收敛速度缓慢
C1 c2 都不为0 ,称为完全型粒子群算法。完全型粒子群算法更容易保持收敛速度和搜索效果的均衡,是较好的选择。
3》最大速度 Vm:
作用:在于维护算法的探索能力与开发能力的平衡。
Vm较大时,探索能力增强,但粒子容易飞过最优解·。
Vm较小时,开发能力增强,但容易陷入局部最优。
Vm一般设为没维变量变化范围的10%-20%。
4》邻域的拓扑结构·:
粒子群算法的邻域拓扑结构包括两种,一种是将群体内所有个体都作为粒子的邻域。另一种是只将群体中的部分个体作为粒子的邻域。
邻域拓扑结构——>群体历史最优位置,由此将粒子群算法分全局粒子群算法和局部粒子群算法。
全局粒子群算法:(1)粒子自己历史最优值 (2)粒子群体的全局最优值
局部粒子群算法:(1)粒子自己历史最优值 (2)粒子邻域内粒子的最优值
邻域随迭代次数的增加线性增大,最后邻域扩展到整个粒子群。
经过实践证明:全局版本的粒子群算法收敛速度快,但是容易陷入局部最优。局部版本的粒子群算法收敛速度慢,但是很难陷入局部最优。现在的粒子群算法大都在收敛速度与摆脱局部最优这两个方面下功夫。其实这两个方面是矛盾的。看如何更好的折中了。
5》停止准则:
(1)最大迭代次数
(2)可接受的满意解
6》粒子空间的初始化:
较好地选择粒子的初始化空间,将大大缩短收敛时间.初始化空间根据具体问题的不同而不同,也就是说,这是问题依赖的。
从上面的介绍可以看到,粒子群算法与其他现代优化方法相比的一个明显特色就是所需调整的参数很少.相对来说,惯性因子和邻域定义较为重要.这些为数不多的关键参数的设置却对算法的精度和效率有着显著影响。
六、改进方向
口 对基本粒子群算法更新公式的改进
口 基于遗传思想对粒子群算法的改进
口 利用小生境思想对粒子群算法的改进
七、优点:
简单易行
收敛速度快
设置参数少