最大流问题与Ford-Fulkerson算法介绍

背景

1. 我们有图 G=(V, E)，V是顶点的集合，E是边的集合。
2. 图中边的权重都为非负数 （满足1，2两点有时称之为流网络）。
3. 对于这个图G，有两个顶点很重要，一个是源头s，一个是汇聚点t，我们想考虑的是从源头s流向汇聚点t的流。

我们想要解决的问题：在一个流里，有着每条边的运载能力限制，我最多能从源头运输多少数量到目的地。

那么什么是流呢？

流的定义

定义：直观来说，流就像它的名字一样，从源头s运送一些“东西”到汇聚点t，比如下水道系统运输水流，公路网络运输车流。

流具有三个需要注意的点！！

1. 对于图中非s和t的普通结点，流进量等于流出量
2. 我们非常关心总运输流量，比如这个下水道系统，究竟从s点到t点最多能运输多少立方米的水？我们把它记成|f|，这个|f|极其重要，是我们研究的目的所在。
3. 当然，每条边是有运输上限的，就像某条公路车流是有上限的一样，若运输量无穷无尽，我们的研究也就没有意义了。我们将从u点到v点的运输上限，或者说是运载能力记为c(u,v)。对于从u点到v点的流量，记作f(u,v)。显然对所有边(u,v)我们有f(u,v)<=c(u,v)。

研究目的：最大化|f| (|f|的定义在上面第二点)，在一个流网络里，有着每条边的运载能力限制，我最多能从s运输多少东西到t。

总结一下，流可以看成一个图，满足两个条件：
1.除了s和t，流入等于流出。
2.所有边的流量f小于运载量c。(flow < capacity)
让我们来看一个流的例子：

此图中除了s和t，流入等于流出，每条边的流量小于运载上限(比如10/20，10是流量，20是上限)。

那么这个图中我们关心的总运输量是多少呢？

是10！直观来想，从s流出10的流量，在复杂网络中经过一系列流入等于流出的操作，最终汇入t，这就是总流量的定义：从s运输到t的流量数。

所以提及总流量，我们盯着s看就好了。

回忆起我们的研究目的，其实就是想寻找一个最大的|f|，此例中|f|=10，还能更大吗？

这就是最大流问题：寻找满足运载上限的最大流。
为了解决这个问题，我们引进割，那么割是什么呢？

割的定义

割说白了，就是对于点的分割，有了流的基础，我们直接看例子。

左右两个黄色的区域，说白了就是点的集合，正式一点来说，我们把它记成(S,S’)，比如左黄区域为S(源头s在S里)，右黄区域为S’(目的地t在S’里)。
割很随意，但是有个要求，就是s和t要属于不同的区域！

对于割，我们只关心一个事情：从S到S’的总运载上限cap(S,S’)，就是割的容量。
在这里，我们不关心从S到S’的流，不关心从S’到S的总运载上限，比如这个例子里，cap(S,S’)=5+10=15，而不是等于5+10+15=30。

这个定义还挺死板的，总结一下，割形成了两个区域，我们关心的是两个区域之间“桥梁”的运载量之和，桥梁的方向一定是一致的，比如都是从S到S’的方向。

在我们知道了所有割的容量后，我们最想知道的是这其中最小的那个容量，即最小割的容量。

说完了割，还是没有说到为什么这个概念的引进可以解决最大流问题，我们接下来看看最大流最小割的关系。

最大流最小割

我们回忆一下，流是一个边权重非负的图，流入等于流出。割是把流分成两个区域，s和t分布于不同的区域。

最小割大于等于最大流，因为只有这样，流才能顺利从一个区域运输到另一个区域（想想流要通过从S到S’的桥梁）。

换言之，对于任意一个割(S,S’)，最大流都要小于等于cap(S,S’)，因为我研究的是从源头s到t，可以想成是从S区域到S’区域，那么我运输的流量肯定要小于等于桥梁的总限制。

所以我们有了第一个关系式：max|f| <= cap(S,S’)

关键的来了，这个关系式的上界取等发生在(S,S’)是最小割。这个被称为最大流最小割定理，所以我们完成了转化，将寻找最大流问题转化为了寻找最小割的问题。

那么如何找到最小割呢？
首先引进两个术语：saturate和avoid，这两个词都是形容流f对边e)的。还是很形象的，一个充满一个避开。
f saturates e: 即f(e) = c(e)，就是流量充满了运载上限，比如10/10。
f avoids e: f(e) = 0
有这两个术语后，我们有方法如下：
f是一个流，(S, S’)是一个割，如果f充满了从S到S’的每一座桥，避开了从S’到S的每一座桥，则f是一个最大流，(S, S’)是一个最小割。
那么为什么最大流等于最小割的总运载上限呢？（关于这个问题的解答，还是开一篇新的文章吧）
先不考虑为什么，我们先介绍如何找到最大流的算法，即Ford-Fulkerson算法。

Ford-Fulkerson

首先这个算法有个重要的工具：残存网络。残存网络其实就是具有残存容量的图。算法导论上有个普遍公式来定义残存容量：

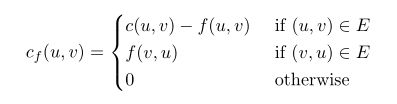
翻译一下公式，说明的就是对于两点间的残存容量定义为：
1.如果这两点连线原来就是原图的边，那么它的残存容量等于运载上限-运输流量。
2.如果这两点的反向连线是原图的边，那么它的残存容量等于那条边的运输流量。
3.其他情况是0，当做没连通。

很不直观呀，所以我们结合例子来说明说明残存容量以及残存网络。
首先先明确一下，在残存网络中我们只关心运载上限（就是残存容量啦）。

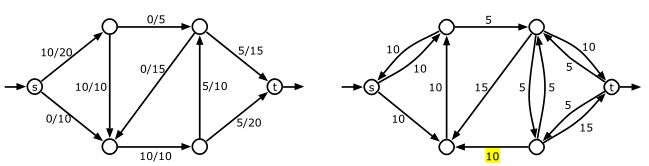
这个例子中，左边是原图，右边是残存网络。
我们先来看源头s和它右上角的结点a（就是10/20相连的那两点），为什么转换成残存网络中形成了一个10和10的圈？
我们回到不直观的公式定义，c_f(s,a)应该是等于20-10的，因为(s,a)是原图的边。那么c_f(a,s)是多少呢，因为这个的反向连线在原图里是(s,a)是边，所以c_f(a,s) = f(s,a) = 10
那么直观来说怎么生成残存网络呢，原图的每条边都需要拆解，比如考虑那条5/15的从b指向t的边，我们画在残存网络中就是生成一条15-5容量的边，从b指向t，然后生成一个5的边，从t指向b。（不用为b是哪个点感到困惑，其实就是例子中t左上角的那个点）如果发现容量为0的边，就不用画在残存网络里了。
请在例子里练练手，找上几个残存容量你就掌握了如何生成残存网络的方法了。

接下来我们看看残存网络对我们的帮助：
1.残存网络中没有从s到t的路径时，最大流等于最小割容量。
2.残存网络中有从s到t的路径时，最大流不等于最小割容量。
关于以上两点的证明用到了割，会在新一篇文章说到。

如果是情况2：我们考虑路径P：s->v₀->v₁->v₂->… ->v_n ->t，把它叫增广路径。在增广路径中找最小的c_f，记作F。在这种残存网络还有路径从s通向t的情况中，我们没有做到最好，我们要把F纳入我们对于流的更新，直到找不到增广路径为止，更新方法如下：

做了这么多铺垫，又是残存网络，又是对流的更新，接下来介绍Ford-Fulkerson算法。
我们从0流量出发（此时残存网络就是原图），找到增广路径（注意增广路径一定是在残存网络里找），接着把流更新，直到残存网络中没有增广路径（就是没有路径从s到t啦）为止。下面我们还是看例子：

在示例中，左边是残存网络，右边是更新后的原图。一开始(a)的残存网络就是原图，我们找了条增广路径（粗线），找到了最小的c_f，就是4，然后把4引入了原图的流更新。
从(a)更新后的原图，我们可以画出它的残存网络，于是我们来到了(b)，还是老步骤，找增广路径，找最小的c_f，以它来更新原图（从(a)的右图到(b)的右图）。强烈推荐从c往后自己将这个过程找完，花几分钟找完你就记住了Ford-Fulkerson算法。答案如下，增广路径选取不同，过程可能不一样，但是最大流都是一样的，就是23：

在(f)中，我们再也无法找到增广路径，所以我们的算法结束，这是我们的最大流。

总结一下，我们要解决的问题是在一个有运载限制的网络系统中，从s到t最多能运输多少流量。我们引进了流，割的概念，将我们研究的问题转化为寻找最大流。
如何找最大流？采用Ford-Fulkerson算法，从0流量开始，生成残存网络，找到增广路径，从增广路径中找到最小的残存容量F，用F来更新原图，得到新的原图后，循环上述过程直到残存网络中找不到增广路径。此时的原图中，就有了我们想求的最大流。
那么我们引进割是为什么呢，是为了证明Ford-Fulkerson算法的正确性。这个可以开一篇新的文章来说，想要理解Ford-Fulkerson的运行过程看这篇文章就够了，如果想知道为什么Ford-Fulkerson可以找到最大流，那么请看下一篇博客。