【计组实验】P1 logisim完成单周期处理器开发 MIPS指令集

参考教材：《计算机组成与设计 硬件/软件接口 原书第五版》第二章 第四章
↑ 这本书写的特别好，零基础也可以看

实验报告
链接: https://pan.baidu.com/s/19YQA6YxejrAD9To6lbu5Zw
提取码: wj38

完整电路
链接: https://pan.baidu.com/s/1m028MjBr0ntW9NQIeyo-Rw
提取码: byv8

*仅供参考，指令已经过MARS对比测试，但不保证完全正确，欢迎指正
*最后一次更新：2019-6-21 14:34:17 (新增：七段数码管、JAL指令)

顶层视图

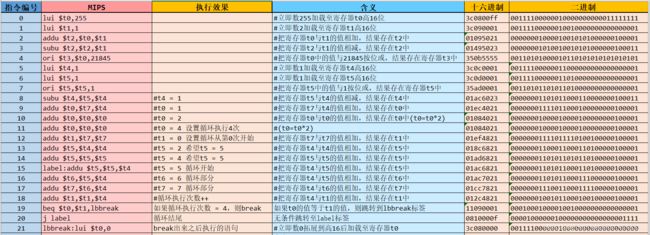
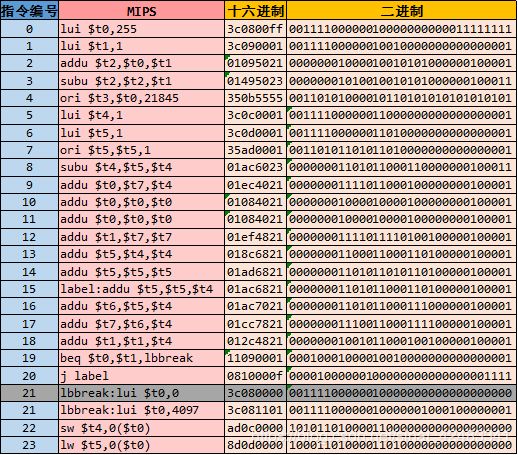
测试指令：

v2.0 raw
3c0800ff 3c090001 01095021 01495023 350b5555 3c0c0001 3c0d0001 35ad0001 01ac6023 01ec4021 01084021 01084021 01ef4821 018c6821 01ad6821 01ac6821 01ac7021 01cc7821 012c4821 11090001 0810000f 3c080000 ad0c0000 8d0d0000 0c100000

指令解释：

测试结果（运行最后一条指令JAL之前）：

实验要求

以下为制作过程记录

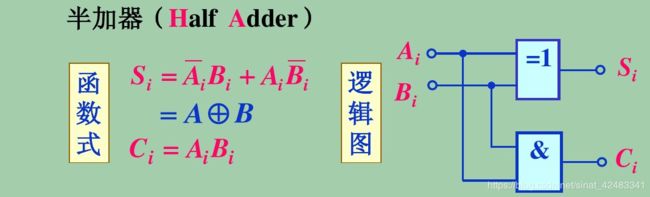
半加器

此半加器将在32-bit adder的第0位使用，因为第0位不需要考虑低位的进位

半加器电路是指对两个输入数据位相加，输出一个结果位和进位，没有进位输入的加法器电路。

是实现两个一位二进制数的加法运算电路。

判断是否进位的电路

或门的使用

或门有多个输入端，一个输出端，只要输入中有一个为高电平时（逻辑“1”），输出就为高电平（逻辑“1”）；只有当所有的输入全为低电平（逻辑“0”）时，输出才为低电平（逻辑“0”）

下图是一个3输入的或门：

下面这个电路用来判断是否进位，有3个输入，1个输出。真值表如右图：

全加器 full adder

用门电路实现两个二进制数相加并求出和的组合线路，称为一位全加器。

一位全加器可以处理低位进位，并输出本位加法进位。

多个一位全加器进行级联可以得到多位全加器。

下面图左是一个一位全加器，图右是对应的真值表。电路上面是异或，下面方块用于判断是否进位。

3个输入分别是：两个加数a(i),b(i)，前一位的进位c(i)
2个输出分别是：本位的结果s(i)，下一位进位c(i+1)

异或门的使用

如下图，使用了一个三输入的异或门

在实际使用时，注意左侧的Multiple-Input Behavior选项
应该选择“When an odd number are on”,这样当三个输入为1 1 1时，输出为1
不要选择When one input is on，否则三个输入为1 1 1时，输出为 0

上图中三输入异或门的真值表如下：A B C是输入，Y是输出，F是对输出的取反

为什么会产生这样的真值表？解释如下。

当有多于2个输入时，异或逻辑的运算（半加运算）

异或运算通常用符号“♁”表示，其运算规则为：

0♁0=0 0同0异或，结果为0

0♁1=1 0同1异或，结果为1

1♁0=1 1同0异或，结果为1

1♁1=0 1同1异或，结果为0

即两个逻辑变量相异，输出才为1，给ABCD赋值，从左向右累计运算。得答案。

第一、相信你是知道两个命题变量的异或运算的规则的——只要你知道它的真值表就够了，其规律是：（两变量取值）相同则（结果为）假，不同则真；

第二、你应该知道两个命题变量的异或运算的结果也是一个命题变量，它可以参与下一步的逻辑运算；

第三、多个异或连续运算，就类似数学上的连加、连乘运算：将前两个数的运算结果，与第三个数继续运算；再将结果与第四个运算；再……其中的每一步都要按照相应运算的规则进行；

现在，你可以自己进行计算了。不过我曾经对多个变量的异或（和同或）运算的规律做过分析，现将结果告诉你，你可以自行验证：

1、多个命题的“异或”运算：其结果依赖于参与运算的所有量中，取值为“真”的量的“个数”的“奇偶性”：

若含“奇数”个“真命题”，则结果为“真”；

若含“偶数”个“真命题”，则结果为“假”；（零个也是偶数个）

换句话说：命题表达式 A♁B♁C♁D 结果为“真”，当且仅当 A、B、C、D 中有奇数个（即 1 个或 3 个）变量的取值为“真”；而至于其中“假命题”的个数，则对结果“无任何影响”。关于这一点的证明，可以从下面两个恒等式中找到思路：

p ♁ 1 = 非p；——增加一个“真命题”参与运算，总会将“原命题”变成其“反命题”；

p ♁ 0 = p；——增加一个“假命题”参与运算，对“原命题”永远没影响；

2、多个命题的“同或”运算：其结果依赖于参与运算的所有量中，取值为“假”的量的“个数”的“奇偶性”：

若含“奇数”个“假命题”，则结果为“假”；

若含“偶数”个“假命题”，则结果为“真”；

32-bit adder

第一步：添加两个32位输入，一个32位输出

做一些tunnel，避免凌乱的电路

B的tunnel也做好了

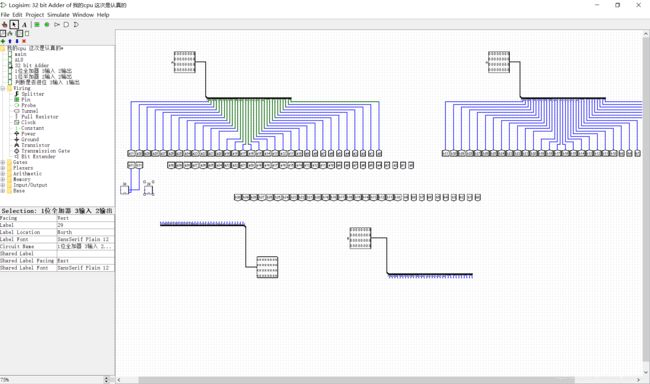
中间过程不详细描述了

1位全加器连在一起，最右面是1位半加器，因为第0位不需要考虑低位进位

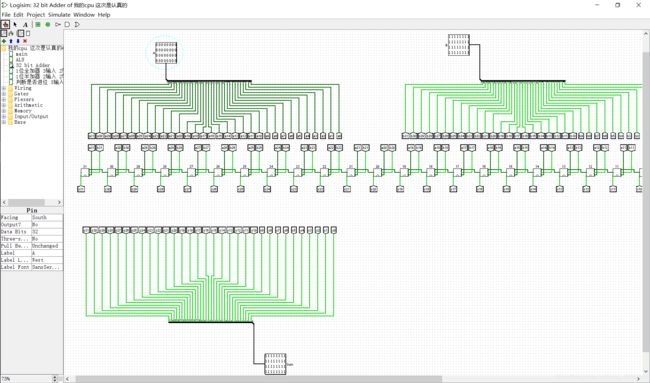
一张图放不下，截一个右边的图吧

32 bit substract

32位减法器，在32位加法器的基础上制作，把减数取反加一（0x1,设置如下），与被减数相加即可

以下：完整的32位减法器

32 bit ori

或门

如果几个条件中，只要有一个条件得到满足，某事件就会发生，这种关系叫做“或”逻辑关系。具有“或”逻辑关系的电路叫做或门。或门有多个输入端，一个输出端。

只要输入中有一个为高电平时（逻辑“1”），输出就为高电平（逻辑“1”）；
只有当所有的输入全为低电平（逻辑“0”）时，输出才为低电平（逻辑“0”）。

32位或的电路实现

32-bit ori用于实现mips的ori指令。电路比较简单，图如下

ALU

算术逻辑单元(arithmetic and logic unit) 是能实现多组算术运算和逻辑运算的组合逻辑电路。
大部分ALU都可以完成以下运算∶
1、整数算术运算（加、减，有时还包括乘和除，不过成本较高）
2、位逻辑运算（与、或、非、异或）
3、移位运算（将一个字向左或向右移位或浮动特定位，而无符号延伸），移位可被认为是乘以2或除以2。

bgez指令
指令用法为：bgez rs, offset
指令作用为：if rs ≥ 0 then branch，如果地址为rs的通用寄存器的值大于等于0，那么发生转移。

Multiplexer
多路选择器是数据选择器的别称。在多路数据传送过程中，能够根据需要将其中任意一路选出来的电路，叫做数据选择器，也称多路选择器或多路开关

用下图理解一下多路选择器的作用：
choose=0时，输入A有效，输入B无效
choose=1时，输入A无效，输入B有效

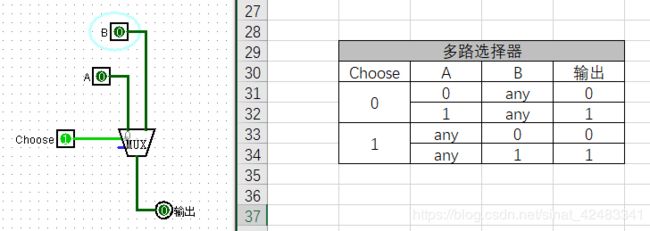
再用下面两张图理解一下select bits=2 的情况

ALU整体电路图

ALU实现Add、Sub、Ori的功能，用了两个mux，上面的mux用于执行bgnz指令，下面的mux用于输出执行的到底是哪一种运算（加、减还是或）。实际上，当A（上面）、B（下面）输入都存在时，每一种运算都已经进行了，只不过由于下方mux的选择，运算结果没有输出而已。

对于黄色圈内bgnz原理的解释、Multiplexer在本电路中的作用，如下图：
（后来我把bgnz删了，因为实验要求里并没有让写这条指令）

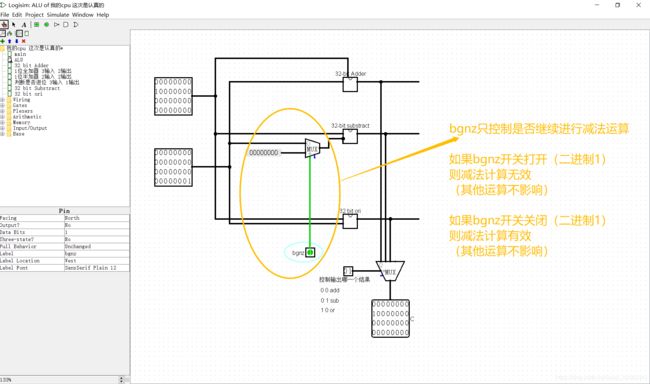
至此，ALU的设计完成

存储原件（与本实验无关，可跳过）

锁存器与触发器P469

S-R锁存器
可以存储一位数据，数值存储在如下图所示的交叉耦合结构内


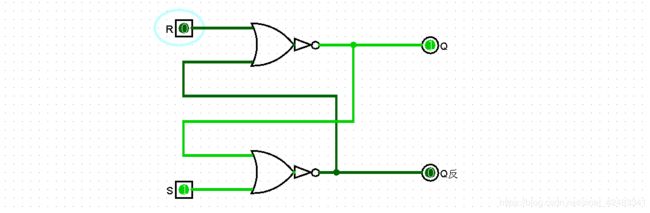
D锁存器
当锁存器处于打开状态时，输出Q的值随输入D的改变而变化。

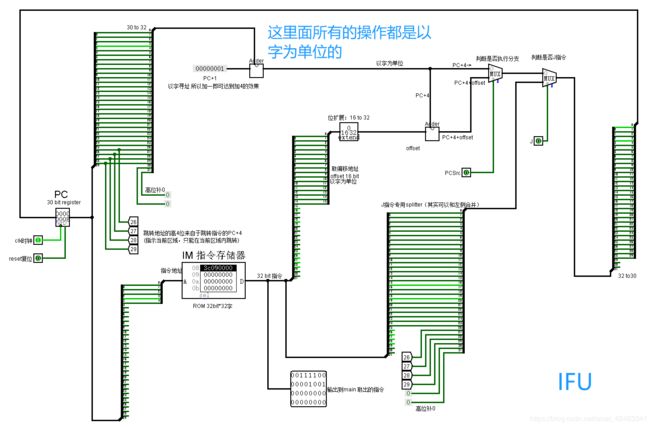
IFU

作用：存储指令、读出指令

要求
4. IFU：内部包括PC、IM(指令存储器)及相关逻辑。
a) PC：用寄存器实现，宽度为30位。PC应具有复位功能。
b) IM：容量为32bit×32字，用ROM实现。
c) 说明：由于IM地址仅为5位，因此请用2个对接的Splitter实现将PC低位地址与IM地址连接。

解释：关于为什么PC宽度为30位，而IM宽度为32位

IM：容量为32bit×32字，用ROM实现

IFU整体图（右下角独立的部分没用，没舍得删）

一些易错点

Controller

作用：判断执行的是哪一条指令，按照真值表输出控制信号来控制main电路中的许多multiplexer

整体视图↓

分区域放大

左边↓

右边↓

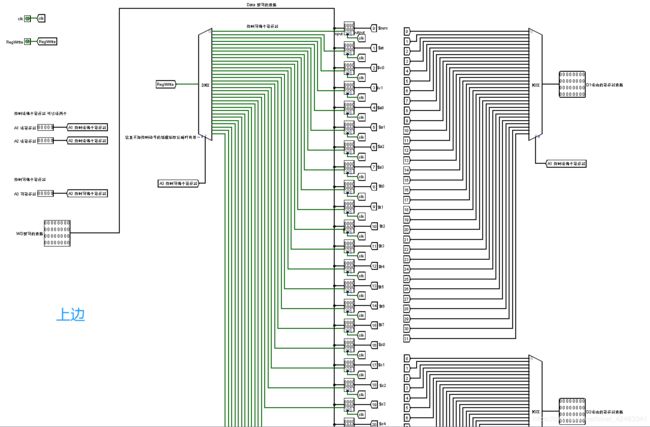
Regfile寄存器堆

Extender位拓展器

顶层视图 main

整体↓

详细图↓



至此，CPU设计完成，下面的步骤就是测试指令了
首先给出MIPS寄存器号对应表

MIPS寄存器号表

写了一些测试数据
（0）
lui $t0,255 #立即数加载至寄存器t0高16位
001111 00000 01000 0000000011111111
00111100000010000000000011111111
3c0800ff

（1）
lui $t1,1 #立即数加载至寄存器t1高16位
00111100000010010000000000000001
3c090001

（2）
addu $t2,$t0,$t1 #把寄存器t0与t1的值相加，结果存在t2中
000000 t0 t1 t2 00000 100100
操作码 源1 源2 目的
000000 01000 01001 01010 00000 100001
00000001000010010101000000100001
01095021

（3）
subu $t2,$t2,$t1 #把寄存器t2与t1的值相减，结果存在t2中
操作码 源1 源2 目的
00000001010010010101000000100011
01495023

（4）
ori $t3,$t0,0101010101010101 #把寄存器t0中的值与imm16相与，结果存在寄存器t3中
操作码 源 目的
001101 t0 t3 imm16
00110101000010110101010101010101
350b5555
预期：t3 0000 0000 0101 0101 0101 0101

（5）
sw $t3,1($t4) #把寄存器t3中的数放进以t4中存的0为base，2为偏移的内存单元中（效果为2字，因为以字寻址）
101011 01100 01011 0000000000000010
10101101100010110000000000000010
ad8b0002

（6）
lw $t5,1($t4) #把以t4中存的0为base，2为偏移的内存单元中的数据，存放在寄存器t5中
100011 01100 01101 0000000000000010
10001101100011010000000000000010
8d8d0002

• 以上运行结果：
  t0: 00ff 0000
  t1: 0001 0000
  t2: 00ff 0000
  t3: 00ff 5555
  t4: 0000 0000
  t5: 00ff 5555

（7）
beq $t3,$t5,(十进制7)0000000000000111 #比较t3和t5的数据，相等就跳转到PC+7（字）
000100 01011 01101 0000000000000111 #如果不相等，就执行下一条指令PC+1（字）
00010001011011010000000000000111
116d0007

（8）
lui $t1,0 #立即数0加载至寄存器t1高16位（把t1清零）
00111100000010010000000000000000
3c090000

（14）
lui $t0,0 #立即数0加载至寄存器t0高16位（把t0清零）
001111 00000 01000 0000000000000000
00111100000010000000000000000000
3c080000

（15）
j 8 #跳转回到第8条指令（0,1,2,3,4,5,6,7,8）
00001000000000000000000000001001
08000008

• 以上运行结果：
  t0: 0000 0000
  t1: 0000 0000
  t2: 00ff 0000
  t3: 00ff 5555
  t4: 0000 0000
  t5: 00ff 5555

要注意，beq是相对下一条指令寻址，j是绝对地址

全部指令