经典大数据面试题
什么是大数据?
大数据(big data,mega data),或称巨量资料,指的是需要新处理模式才能具有更强的决策力、洞察力和流程优化能力的海量、高增长率和多样化的信息资产。 在维克托·迈尔-舍恩伯格及肯尼斯·库克耶编写的《大数据时代》中大数据指不用随机分析法(抽样调查)这样的捷径,而采用所有数据进行分析处理。大数据的4V特点:Volume(大量)、Velocity(高速)、Variety(多样)、Value(价值)。
1>给一个超过100G大小的log file,log中存着IP地址 ,设计算法找到出现次数最多的IP地址?
答:首先看到100G的日志文件,我们的第一反应肯定 是太大了,根本加载不到内存,更别说设计算法了, 那么怎么办呢?既然装不下,我们是不是可以将其切 分开来,一小部分一小部分轮流进入内存呢,答案当然是肯定的。
在这里要记住一点:但凡是大数据的问题,都可通过 切分来解决它。
粗略算一下:如果我们将其分成1000个小文件,每个文件大概就是500M左右的样子,
现在计算机肯定轻轻 松松就能装下。
那么,问题又来了,怎样才能保证相 同的IP被分到同一个文件中呢?
这里我想到的是哈希切分,使用相同的散列函数(如 BKDRHash)将所有IP地址转换为一个整数key,
再利用 index=key%1000就可将相同IP分到同一个文件。
依次将这1000个文件读入内存,出现次数最多的IP进行统计。
最后,在1000个出现次数最多的IP中找出最大的出现次数即为所求。
用到的散列函数:
template
size_t BKDRHash(const T *str)
{
register size_t hash = 0;
while (size_t ch = (size_t)*str++)
{
hash = hash * 131 + ch; // 也可以乘以31、131、1313、13131、131313..
}
return hash;
} 2>与上题条件相同,如何找到TOP K的IP?
答:这倒题说白了就是找前K个出现次数最多的IP,即 降序排列IP出现的次数。
与上题类似,我们用哈希切分对分割的第一个个小文件中出现最多的前K个IP建小堆,
然后读入第二个文件,将其出现次数最多的前K个IP与 堆中数据进行对比,
如果包含大于堆中的IP出现次数,则更新小堆,替换原堆中次数的出现少的数据
再读入第三个文件,以此类推……
直到1000个文件全部读完,堆中出现的K个IP即是出现 次数最多的前K个IP地址。
3>给定100亿个整数,设计算法找到只出现一次的整数 ?
答:看到此题目,我的第一反应就是估算其占用内存 的大小:100亿个int,一个int4个字节,100亿*4=400 亿字节
又因为42亿字节约等于4G,所以100亿个整数大概占用 的内存为40G,一次加载到内存显然是不太现实的。
反过来想,所有整数所能表示的范围为2^32,即16G, 故给出的数据有很多数据是重复的。
解法1:哈希切分
与第一题类似,用哈希切分将这些数据分到100个文件 中,每个文件大约400M,
将每一个文件依次加载到内存中,利用哈希表统计出 现一次的整数,
将100个文件中出现一次的整数汇总起来即为所求。
解法2:位图变形
我们知道,位图是利用每一位来表示一个整数是否存 在来节省空间,1表示存在,0表示不存在。
而上题对于所有整数而言,却有三种状态:不存在、 存在一次、存在多次。
故此,我们需要对传统位图进行扩展,用两位来表示 一个整数的状态:00表示不存在、
01表示存在一次, 10表示存在多次,11表示无效状态。
按照上述表示,两位表示一个整数状态,所有整数只 需要1G即可表示其存在与否。
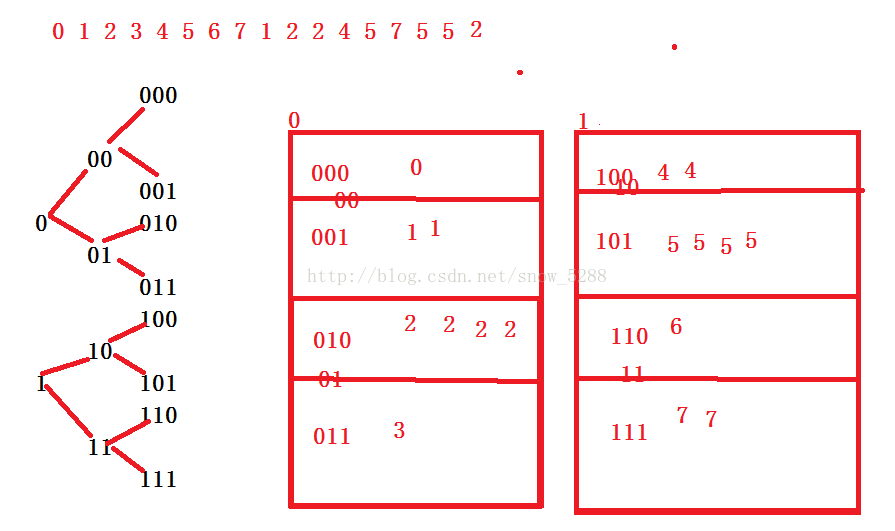
解法3:
众所周知,一个整数占32位,那么我们可对每一位按 照0和1将其分为两个文件,
直到划分到最低位,如果 被分的文件中哪个文件只包含一个数据,那么,此数据即为只出现一次的整数。
如下图:
4>给两个文件,分别有100亿个整数,我们只有1G内存 ,如何找到两个文件交集?
答:100亿*4字节 = 400亿字节 = 40G
解法1:普通查找
将其中的一个文件分为100个小文件,每一份占400M, 将每一小份轮流加到内存中,
与第二个文件中的数据进行对比,找到交集。此种算 法时间复杂度为O(N*N)。
解法2:哈希切分
对两个文件分别进行哈希切分,将其分为100个小文件 ,index=key%100(index为文件下标)
将两个文件中下标相同的小文件进行对比,找出其交 集。
将100个文件的交集汇总起来即为所给文件的文件交集 。此种算法时间复杂度为O(N)。
解法3:位图
我们知道,位图中的每一位就可代表一个整数的存在 与否,而16G的整数用位图512M即可表示,
将第一个文件中的整数映射到位图中去,拿第二个文件中的数字到第一个文件映射的位图中去 对比,
相同数字存在即为交集。此种算法时间复杂度 为O(N)。
注意:重复出现的数字交集中只会出现一次。
位图的简单模拟:
//位图:专门用来判断数据是否存在,不能统计数据出现的次数
class BitMap
{
public:
BitMap(size_t N = 1024)//N代表需要判断的数据个数
{
_array.resize((N>>5) + 1);//相当于(N/32)+1,结果为需要开辟的字节个数
}
void Set(size_t value)//将状态由无置为有,即0变为1
{
size_t index = value >> 5;//代表整数的下标,即第几个整数
size_t num = value % 32;//代表第几位
_array[index] |= 1<> 5;//代表整数的下标,即第几个整数
size_t num = value % 32;//代表第几位
_array[index] &= (~(1<> 5;//代表整数的下标,即第几个整数
size_t num = value % 32;//代表第几位
return _array[index] & (1< _array;//每个size_t可判断32个数是否存在
};
void TestBitMap()
{
BitMap bm((size_t)-1);
bm.Set(2);
bm.Set(20);
bm.Set(200);
bm.Set(2000);
bm.Set(20000);
bm.Set(200000);
bm.Set(2000000);
bm.Set(20000000);
bm.ReSet(2);
bm.ReSet(2000);
bm.ReSet(2000000);
bm.ReSet(20000000);
cout< 
5>1个文件有100亿个int,1G内存,设计算法找到出现 次数不超过两次的所有整数?
答:类似题目3
解法1:哈希切分
与第一题类似,用哈希切分将这些数据分到100个文件 中,每个文件大约400M,
将每一个文件依次加载到内存中,利用哈希表统计出 现不超过两次的整数
将100个文件中出现不超过两次的整数汇总起来即为所求。
解法2:位图变形
我们知道,位图是利用每一位来表示一个整数是否存 在来节省空间,1表示存在,0表示不存在。
而上题对于所有整数而言,却有三种状态:不存在、 存在一次、存在多次。
故此,我们需要对传统位图进行扩展,用两位来表示 一个整数的状态:00表示不存在、
01表示存在一次, 10表示存在两次,11表示出现超过两次。
按照上述表示,两位表示一个整数状态,所有整数只需要1G即可表示其存在次数。
6>给两个文件,分别有100亿个query,我们只有1G内 存,如何找到两个文件交集?分别给出精确算法和近 似算法。
答:类似于第四题,
100亿*4字节 = 400亿字节 = 40G
精确算法:哈希切分
对两个文件分别进行哈希切分,使用相同的散列函数 (如 BKDRHash散列函数)将所有query
转换为一个整数key ,再利用 index=key%1000就可将相同query分到同一 个文件。(index为文件下标)
将两个文件中下标相同的小文件进行对比,找出其交 集。
将100个文件的交集汇总起来即为所给文件的文件交集 。此种算法时间复杂度为O(N)。
近似算法:布隆过滤器
首先使用相同的散列函数(如 BKDRHash散列函数)将所有 query转换为一个整数key,
又因为布隆过滤器中的每 一位就可代表一个整数的存在 与否,而16G的整数用 位图512M即可表示,
将第一个文件中的整数映射到位图中去,
拿第二个文件中的数字到第一个文件映射的位图中去对比,相同数字存在即为交集。
此种算法时间复杂度为O(N)。
注意:布隆过滤器判断不存在是确定的,而存存在在可能导致误判,所以称近似算法。
布隆过滤器的简单模拟:
各种不同的散列函数:
template
size_t BKDRHash(const T *str)
{
register size_t hash = 0;
while (size_t ch = (size_t)*str++)
{
hash = hash * 131 + ch; // 也可以乘以31、131、1313、13131、131313..
}
return hash;
}
template
size_t SDBMHash(const T *str)
{
register size_t hash = 0;
while (size_t ch = (size_t)*str++)
{
hash = 65599 * hash + ch;
//hash = (size_t)ch + (hash << 6) + (hash << 16) - hash;
}
return hash;
}
template
size_t RSHash(const T *str)
{
register size_t hash = 0;
size_t magic = 63689;
while (size_t ch = (size_t)*str++)
{
hash = hash * magic + ch;
magic *= 378551;
}
return hash;
}
template
size_t APHash(const T *str)
{
register size_t hash = 0;
size_t ch;
for (long i = 0; ch = (size_t)*str++; i++)
{
if ((i & 1) == 0)
{
hash ^= ((hash << 7) ^ ch ^ (hash >> 3));
}
else
{
hash ^= (~((hash << 11) ^ ch ^ (hash >> 5)));
}
}
return hash;
}
template
size_t JSHash(const T *str)
{
if(!*str) // 这是由本人添加,以保证空字符串返回哈希值0
return 0;
register size_t hash = 1315423911;
while (size_t ch = (size_t)*str++)
{
hash ^= ((hash << 5) + ch + (hash >> 2));
}
return hash;
}
template
size_t DEKHash(const T* str)
{
if(!*str) // 这是由本人添加,以保证空字符串返回哈希值0
return 0;
register size_t hash = 1315423911;
while (size_t ch = (size_t)*str++)
{
hash = ((hash << 5) ^ (hash >> 27)) ^ ch;
}
return hash;
}
template
size_t FNVHash(const T* str)
{
if(!*str) // 这是由本人添加,以保证空字符串返回哈希值0
return 0;
register size_t hash = 2166136261;
while (size_t ch = (size_t)*str++)
{
hash *= 16777619;
hash ^= ch;
}
return hash;
}
template
size_t DJBHash(const T *str)
{
if(!*str) // 这是由本人添加,以保证空字符串返回哈希值0
return 0;
register size_t hash = 5381;
while (size_t ch = (size_t)*str++)
{
hash += (hash << 5) + ch;
}
return hash;
}
template
size_t DJB2Hash(const T *str)
{
if(!*str) // 这是由本人添加,以保证空字符串返回哈希值0
return 0;
register size_t hash = 5381;
while (size_t ch = (size_t)*str++)
{
hash = hash * 33 ^ ch;
}
return hash;
}
template
size_t PJWHash(const T *str)
{
static const size_t TotalBits = sizeof(size_t) * 8;
static const size_t ThreeQuarters = (TotalBits * 3) / 4;
static const size_t OneEighth = TotalBits / 8;
static const size_t HighBits = ((size_t)-1) << (TotalBits - OneEighth);
register size_t hash = 0;
size_t magic = 0;
while (size_t ch = (size_t)*str++)
{
hash = (hash << OneEighth) + ch;
if ((magic = hash & HighBits) != 0)
{
hash = ((hash ^ (magic >> ThreeQuarters)) & (~HighBits));
}
}
return hash;
}
template
size_t ELFHash(const T *str)
{
static const size_t TotalBits = sizeof(size_t) * 8;
static const size_t ThreeQuarters = (TotalBits * 3) / 4;
static const size_t OneEighth = TotalBits / 8;
static const size_t HighBits = ((size_t)-1) << (TotalBits - OneEighth);
register size_t hash = 0;
size_t magic = 0;
while (size_t ch = (size_t)*str++)
{
hash = (hash << OneEighth) + ch;
if ((magic = hash & HighBits) != 0)
{
hash ^= (magic >> ThreeQuarters);
hash &= ~magic;
}
}
return hash;
}
//布隆过滤器
struct __HashFunc1
{
size_t operator()(const std::string& s)
{
return BKDRHash(s.c_str());
}
};
struct __HashFunc2
{
size_t operator()(const std::string& s)
{
return SDBMHash(s.c_str());
}
};
struct __HashFunc3
{
size_t operator()(const std::string& s)
{
return RSHash(s.c_str());
}
};
struct __HashFunc4
{
size_t operator()(const std::string& s)
{
return JSHash(s.c_str());
}
};
struct __HashFunc5
{
size_t operator()(const std::string& s)
{
return APHash(s.c_str());
}
};
template
class BloomFilter
{
public:
BloomFilter(size_t N = 1024)
:_bm(N * 10)
,_size(N * 10)
{}
void Set(const K& key)
{
size_t hash1 = HashFunc1()(key) % _size;
size_t hash2 = HashFunc2()(key) % _size;
size_t hash3 = HashFunc3()(key) % _size;
size_t hash4 = HashFunc4()(key) % _size;
size_t hash5 = HashFunc5()(key) % _size;
_bm.Set(hash1);
_bm.Set(hash2);
_bm.Set(hash3);
_bm.Set(hash4);
_bm.Set(hash5);
cout< 测试函数:
void TestBloomBitMap()
{
BloomFilter<> bm(1024);
bm.Set("http://www.cnblogs.com/-clq/archive/2012/05/31/2528153.html");
bm.Set("http://www.cnblogs.com/-clq/archive/2012/05/31/2528154.html");
bm.Set("http://www.cnblogs.com/-clq/archive/2012/05/31/2528155.html");
bm.Set("http://www.cnblogs.com/-clq/archive/2012/05/31/2528156.html");
bm.Set("http://www.cnblogs.com/-clq/archive/2012/05/31/2528157.html");
cout<7>如何扩展BloomFilter使得它支持删除元素的操作?
答:因为一个布隆过滤器的key对应多个为位,冲突的 概率比较大,所以不支持删除,因为删除有可能影响 到其他元素。如果要对其元素进行删除,就不得不对 每一个位进行引用计数,同下题。
8>如何扩展BloomFilter使得它支持计数的操作?
答:我们都知道,位图非常的节省空间,但由于每一 位都要引入一个int,所以空间浪费还是比较严重的, 因此不得不放弃位图了,代码如下:
//带删除功能的布隆过滤器(引用计数)
template
class RefBloomFilter
{
public:
RefBloomFilter(size_t N = 1024)
:_size(N * 10)
{
_refbm.resize(_size);
}
void Set(const K& key)
{
size_t hash1 = HashFunc1()(key) % _size;
size_t hash2 = HashFunc2()(key) % _size;
size_t hash3 = HashFunc3()(key) % _size;
size_t hash4 = HashFunc4()(key) % _size;
size_t hash5 = HashFunc5()(key) % _size;
_refbm[hash1]++;
_refbm[hash2]++;
_refbm[hash3]++;
_refbm[hash4]++;
_refbm[hash5]++;
cout< _refbm;
size_t _size;
}; 9>给上千个文件,每一个文件大小为1K-100M,给n个单 词,设计算法对每个词找到所有包含它的文件,你只 有100K内存。
答:对上千个文件生成1000个布隆过滤器,并将1000 个布隆过滤器存入一个文件中,将内存分为两份,一 分用来读取布隆过滤器中的词,一块用来读取文件, 直到每个布隆过滤器读完为止。
用一个文件info 准备用来保存n个词和包含其的文件信息。
首先把n个词分成x份。对每一份用生成一个布 隆过滤器(因为对n个词只生成一个布隆过滤器,内存可能不够用)。把生成的所有布隆过滤器存入外存 的一个文件Filter中。
将内存分为两块缓冲区,一块用于每次读入一个 布隆过滤器,一个用于读文件(读文件这个缓冲区使用 相当于有界生产者消费者问题模型来实现同步),大文 件可以分为更小的文件,但需要存储大文件的标示信 息(如这个小文件是哪个大文件的)。
对读入的每一个单词用内存中的布隆过滤器来判 断是否包含这个值,如果不包含,从Filter文件中读 取下一个布隆过滤器到内存,直到包含或遍历完所有 布隆过滤器。如果包含,更新info 文件。直到处理完 所有数据。删除Filter文件。
10>有一个词典,包含N个英文单词,现在任意给一个 字符串,设计算法找出包含这个字符串的所有英文单 词。
答:对于这道题目,我们要用到一种特殊的数据结 构----字典树来解决它,所谓字典树,又称单词查找树(或Trie树),是一种哈希树的变种。
典型应用:用于统计、排序和保存大量的字符串,经 常被搜索引擎系统用于文本词频统计。
优点:利用字符串的公共前缀来减少查询时间,最大 限度地减少无谓的字符串比较,查询效率高于哈希表 。
基本性质:根节点不包含字符,除根节点外每个节点 都只包含一个字符;
从根节点到某一节点,路径上所有经过的字 符连接起来,为该节点对应的字符串;
每个节点的所有子节点包含的字符都不相同 。
应用:串的快速检索、串排序、最长公共前缀
解:
用给出的N个单词建立一棵与上述字典树不同的字典树 ,用任意字符串与字典树中的每个节点中的单词进行 比较,在每层中查找与任意字符串首字母一样的,找到则遍历其下面的子树,找第二个字母,以此类推, 如果与任意字符串的字符全部相同,则算找到。
如下图: