基于半交互式的裂缝检测方法
裂缝的危害已深入经济社会发展的各个领域,比如交通运输领域中的公路路面裂缝,高速公路隧道壁裂缝等;工业产品领域中的光学玻璃裂缝,木材表面裂缝等等;其安全性检测直接关系到经济发展和安全等重大问题。裂缝虽然大多不足1mm,但是却是一种最常见和最重要的病害表现形式。它一方面预示着病害的出现;另一方面预示潜在的严重安全隐患,比如渗水等因素诱发深层次强度减弱而造成不可估量的损失;同时, 裂缝不及时处理, 将缩短工业产品或公路等的使用寿命。因此,裂缝的快速检测、高效识别和及时养护是提升产品服务质量和延长其使用寿命的有效途径。
裂缝的宽度检测为裂缝检测中最重要的指标。在很长一段时间,各领域中裂缝的检测都依靠有经验的专业人员完成。首先,依靠人眼找到裂缝,然后用游标卡尺量其宽度。它不仅造成严重的人力资源浪费,并且检测的时效性差,精度低,主观性强。一般来说,裂缝的呈现形式复杂多样,使得传统的专业人员检测已不能满足实际的应用需求,这使得基于机器视觉的自动(或半自动)检测技术成为当前的热点研究领域。在此方法中,CCD首先采集目标图像,然后,计算机自动(或半自动)分析图像的内容并且识别裂缝,最后计算宽度指标。在基于数字图像的检测方法中,目标图像的分析和裂缝识别是关键。
目前,常见的处理方法多为传统的图像处理算法,比如阈值分割(参见《Sealed-crack detection algorithm using heuristic thresholding approach》:Kamaliardakani M, Sun L, Ardakani M. Journal of Computing in Civil Engineering, 2014, DOI: 10.1061/(ASCE)CP.1943-5487.0000447),形态学的处理算法(参见《Automated image processing technique for detecting and analysing concrete surface cracks》:Lee B Y, Kim Y Y, Yi S T, Kim J K. Structure and Infrastructure Engineering, 2013,9(6): 567-577),显著性方法(参见《基于图像显著性的路面裂缝检测》:徐威,唐振民,吕建勇. 中国图象图形学报, 2013,18( 1) : 69-77),和特征融合法(参见《基于纹理脊线特征融合的木材表面裂缝检测》:苑玮琦, 李绍丽, 李德健. 仪器仪表学报, 2017, 38(2): 436-444.),此类方法对裂缝的成像质量要求极高,一般需要高对比度,高清晰度以及具备一定几何形态的裂缝;模型学习法(参见《Automatic road crack detection and characterization》:Oliveira H, Correia P L. IEEE Transactions on Intelligent Transportation Systems, 2013, 14(1): 155-168,《基于稀疏表示分类的路面裂缝检测和识别算法》:周舟, 唐振民, 吕建勇等. 信息技术, 2016 (2016 年 11): 21-25和《基于分区域多尺度分析的路面裂缝检测算法》:卢紫微, 吴成东, 陈东岳, 等. 东北大学学报 (自然科学版), 2014, 35(5): 622-625.),该类方法识别精度高,但是对提取的图像特征较敏感,并且需要大量的训练数据,人工标注成本高。近年,基于Hessian矩阵的亚像素级精度的检测器技术,以其精度高和鲁棒性好等特点,在结构光光条中心提取和曲线性结构检测中得到了应用(参见《Steger C. An unbiased detector of curvilinear structures》:Steger. IEEE Transactions on pattern analysis and machine intelligence, 1998, 20(2): 113-125,公开号为CN10149916和CN101178812的中国专利,和《基于Hessian矩阵多尺度滤波的路面裂缝图像检测方法》:王军,孙慧婷,姜志等. 计算机应用,2016,36(S1):174-176,18)。虽然Hessian矩阵的特征向量能很好的表征曲线结构的法线方向和切线方向,但是上述方法中通过泰勒级数展开求取极值点来判定曲线结构的中心和边界,往往受噪声点的影响而得到局部极值点而误判。而(《基于Hessian矩阵多尺度滤波的路面裂缝图像检测方法》:王军,孙慧婷,姜志等. 计算机应用,2016,36(S1):174-176,18)工作中,也仅仅是通过Hessian矩阵的特征向量来识别裂缝的走势。
一些常见的裂缝图像如下所示。通常在实际工程中,图像采集系统往往受光照等外部环境的影响比较大,很难保证纹理清晰的裂缝图像;受裂缝自身宽度、深度、方向的影响, 细微裂缝与背景对比度弱且难以表现出完整的几何形态,而是表现的断断续续, 若隐若现;实际采集的目标图像中背景表现出的不确定性,复杂性和多样性使得现有算法都难以满足实际应用需求,或者只限制于特定的应用场景。比如在隧道检测领域,行业实际应用表明国内外没有任何一种裂缝检测算法能满足实际工程应用需求。

针对上述方法存在的技术问题,我们提供了一种半交互式的裂缝检测方法,解决目前裂缝检测领域中的鲁棒性问题和高精度需求,已专利授权。总的流程框图如下
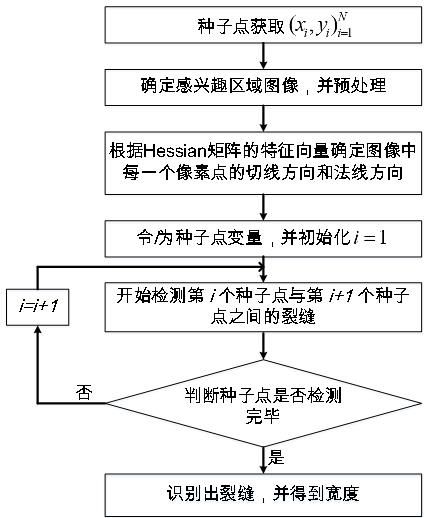
步骤一:种子点选取。用户用鼠标在目标图像上裂缝处选取一系列点坐标记为 ( x i , y i ) i = 1 N ({x_i},{y_i})_{i = 1}^N (xi,yi)i=1N,其中 x x x为水平方向坐标, y y y为竖直方向坐标。注意种子点选取尽量在裂缝大的拐点出选取,如下图所示。点的选取与后续算法设计息息相关,其原理在后续介绍。

步骤二:感兴趣区域提取及图像预处理。为了加快算法的处理效率,我们只需提取裂缝区域图像。具体的提取方法为分别求 N N N个坐标点中最小最大的水平方向坐标值${ {x_{\min }},{x_{\max }}} , 以 及 最 小 最 大 的 竖 直 方 向 坐 标 值 ,以及最小最大的竖直方向坐标值 ,以及最小最大的竖直方向坐标值{ {y_{\min }},{y_{\max }}} 。 那 么 感 兴 趣 区 域 的 左 上 顶 点 坐 标 为 。那么感兴趣区域的左上顶点坐标为 。那么感兴趣区域的左上顶点坐标为({x_{\min }},{y_{\min }}) , 而 右 下 顶 点 坐 标 为 ,而右下顶点坐标为 ,而右下顶点坐标为({x_{\max }},{y_{\max }})$。注意感兴趣区域也可进行适当像素的外扩。进一步,将感兴趣区域图像进行双边滤波操作,在过滤噪声的同时增强裂缝的边缘;然后将滤波后的图像进行对数操作,并去均值归一化,增大裂缝与背景的对比度。
步骤三:计算像素点的切线方向和法线方向。以裂缝区域像素点为例,该点的法线方向对应着灰度值变化最剧烈的方向,而切线方向对应着灰度值变化平缓的方向。显然,裂缝区域内的像素点的切线方向就是裂缝的走势。法线方向向量和切线方向向量正好对应该像素点的Hessian矩阵的特征向量,其基本原理如下:
考虑感兴趣区域图像中某一个像素点 p ( x , y ) p(x,y) p(x,y),其Hessian矩阵为
KaTeX parse error: Unknown column alignment: * at position 32: …{\begin{array}{*̲{20}{c}} {{I_{x…
其中 I x x = ∂ 2 g ( x , y ) ∂ 2 x ⊗ I ( x , y ) {I_{xx}} = \frac{{{\partial ^2}g(x,y)}}{{{\partial ^2}x}} \otimes I(x,y) Ixx=∂2x∂2g(x,y)⊗I(x,y), I y y = ∂ 2 g ( x , y ) ∂ 2 y ⊗ I ( x , y ) {I_{yy}} = \frac{{{\partial ^2}g(x,y)}}{{{\partial ^2}y}} \otimes I(x,y) Iyy=∂2y∂2g(x,y)⊗I(x,y) , I x y = I y x = ∂ 2 g ( x , y ) ∂ x ∂ y ⊗ I ( x , y ) {I_{xy}} = {I_{yx}} = \frac{{{\partial ^2}g(x,y)}}{{\partial x\partial y}} \otimes I(x,y) Ixy=Iyx=∂x∂y∂2g(x,y)⊗I(x,y),其中 I I I为步骤二中增强后的感兴趣区域图像, g ( x , y ) g(x,y) g(x,y)为二维高斯卷积模板,$\otimes $为卷积运算, I ( x , y ) I(x,y) I(x,y)为以像素点 p ( x , y ) p(x,y) p(x,y)为中心且与高斯卷积模板等大小的矩阵。那么Hessian矩阵 H ( x , y ) H(x,y) H(x,y)的最大特征值的绝对值对应的特征向量 n ( p ) = [ n x , n y ] n(p) = [{n_x},{n_y}] n(p)=[nx,ny],为该点的法线方向,而最小特征值的绝对值对应的特征向量 v ( p ) = [ v x , v y ] v(p) = [{v_x},{v_y}] v(p)=[vx,vy],为该点的切线方向。注意,在感兴趣区域图像中每一个像素点都去构造Hessian矩阵进一步求特征向量,运算开销巨大。由于每一个像素点的Hessian矩阵为2维矩阵,其特征向量可以进行数学运算得到一个简单的闭合解。那么在实际工程应用中,将单个像素点的闭合解扩展为矩阵运算,进而求得每一个像素点的切线方向和法线方向。注意,最终的方向向量进行 L 2 L2 L2范数归一化。
步骤四:令 i i i为种子点索引, i i i为自然数, i > 0 i>0 i>0,并初始化为 i = 1 i=1 i=1。
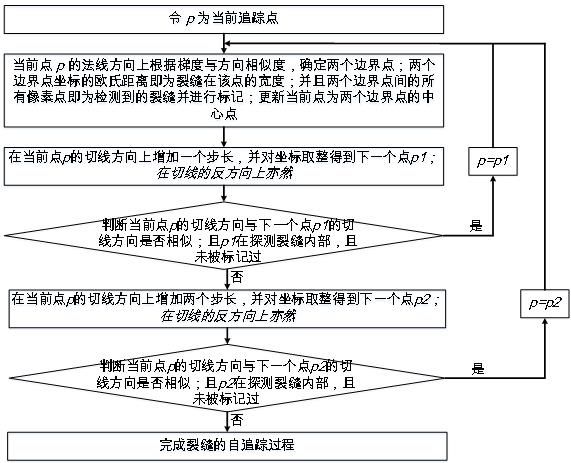
步骤五:开始检测第 i i i个种子点与第 i + 1 i+1 i+1个种子点间的裂缝,主要包括两部分:裂缝自追踪和潜在裂缝点扩展,检测流程下图所示,具体步骤如下:

步骤五-1: 从起始种子点进行裂缝自追踪,并在自追踪过程中不断计算裂缝在当前点的宽度,并标记检测到的裂缝像素点。裂缝自追踪技术详细如下图所示,详细说明如下:
-
令p为自追踪的起始点,并以此点开始进行裂缝的追踪;
-
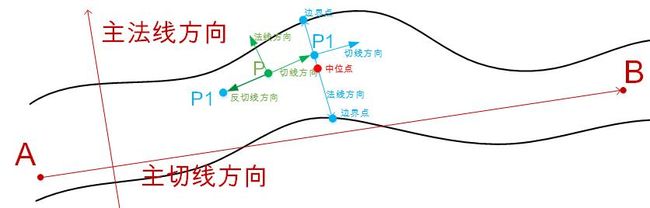
以当前点 p 为零点,在其法线方向上 [ 0 , 30 ] [0,30] [0,30]像素范围内确定该点所在裂缝的两个边界点,判断准则为梯度与切线方向相似度。记当前点p的切线方向为 v ( p ) v(p) v(p),那么在其法线方向上 [ 0 , 30 ] [0,30] [0,30]像素范围内的任何一点 z z z与其的方向相似性度量为 s = v ( p ) T v ( z ) s = v{(p)^T}v(z) s=v(p)Tv(z)。那么点 z z z的响应为 G ( z ) = T ∗ s G(z) = T*s G(z)=T∗s,其中 T T T为该点的梯度。有了这些点的响应,我们就能确定最大值对应的坐标点为当前点所在裂缝的一侧边界点。同理,在当前点p的反法线方向 [ − 30 , 0 ] [-30,0] [−30,0]像素范围内确定另一侧边界点,如下图示。其中像素范围可根据实际情况设定,针对裂缝检测,30个像素是合理的。两个边界点坐标的欧氏距离即为裂缝在该点的宽度;并且两个边界点间的所有像素点即为检测到的裂缝并进行标记;最后更新当前点p为两个边界点之间的中心点。
-
在当前点p的切线方向上增加一个像素步长,并对坐标取整得到下一个点p1;注意在切线的反方向上亦然,,如图3所示。在切线的正反方向上进行点追踪能保证裂缝追踪的完整性,具体说明见后。
-
判断当前点p的切线方向与下一个点p1的切线方向是否相似;且p1在探测裂缝内部,即在两个种子点之间;且p1点未被标记过。注意这里的相似性度量同样采用两点的切线方向向量的内积,如果大于0.9则两点相似。这里的基本原理在于任何曲线在非常邻近的两点之间(这里的两点为相邻的两个像素点)为直线,则直线内所有点的切线方向一致。而判断一个点是否在两个种子点之间,通过起始种子点到该点的方向与该点到终止种子点的方向之间的夹角是否小于 ,或者方向的内积是否大于0。
-
如果p1点满足上述三个条件,则更新当前点p为p1点,执行步骤2)。若不满足执行步骤6)。
-
在当前点p的切线方向上增加两个像素步长,并对坐标取整得到下一个点p2;注意在切线的反方向上亦然。注意如果p1不满足条件,则p1点可能为噪声点。
-
同理判断p2点是否满足上述三个条件。
-
如果p2点满足上述三个条件,则更新当前点p为p2点,执行步骤2)。若不满足,则裂缝自追踪终止。注意如果p2不满足条件,则当前点p的后两个点都出现切线方向突变,表明曲线追踪结束;如果强行在增加三个像素步长,则自追踪可能会偏离裂缝。
步骤五-2: 令 q 为当前追踪点,并初始化为开始种子点。
步骤五-3: 在当前点 q 的主切线方向上增加一个像素步长,并对坐标取整得到下一个点 q1。主切线方向定义为起始种子点到终止种子点的L2范数归一化方向,而主法线方向为主切线方向垂直的L2范数归一化方向,如上图裂缝追踪示意图所示。
步骤五-4: 判断当前点 q ,在其主法线方向上是否有被标记过的像素点。在当前点q的主法线方向上 [ − 30 , 30 ] [-30,30] [−30,30]像素范围内,是否有被检测到的裂缝像素点。如果有,则该点所在的裂缝已经被步骤五-1中自追踪检测到,更新当前点q为q1,执行步骤五-3;若为否,则该点所在裂缝区域还没被检测,即为自追踪的终点处,则执行步骤五-5。
步骤五-5: 在q点,主法线方向上一定范围内,根据灰度值约束,切线方向相似性,和所取点的之前点是否被标记这三个条件进行一系列裂缝点的选取。在该点处表明裂缝自追踪终止,即该点处的切线方向与之前追踪点的切线方向相比出现突变,所以此时的切线方向相似性采用候选点的切线方向与主切线方向进行判断。因此,种子点选取尽量在裂缝大的拐点处选取,尽管裂缝自追踪能自动追踪曲线拐点,但是自追踪过程条件较为严格,很可能出现噪声点干扰,方向突变等因素而追踪不下去。灰度值约束为选取点的灰度值与自追踪的裂缝点的平均灰度值间的差异小于给定阈值。最后的条件为判断候选点在主切线方向一定像素范围内是否有被标记的点,该条件最为关键,直接关系裂缝检测的完整性与连续性。采用此条件的基本思想为裂缝连续性的先验。该步骤将会得到一系列的裂缝点。
步骤五-6: 判断选取的裂缝点个数是否为零。如果为零,表明该点裂缝处至少与前面检测到的裂缝相比出现突变,则跳过该点,更新当前点q为q1,执行步骤五-3。若不为零,则执行步骤五-7。
步骤五-7: 计算一系列潜在点的中位数坐标点,即这些在主法线方向上根据坐标排序的点的中点的坐标。
步骤五-8: 判断该中位数点是否满足灰度值约束和切线方向相似性。注意这里切线方向相似性仍然采用与主切线方向进行判断。如果满足条件,则表明该点为裂缝内部的可靠点,以该点作为起始点进行裂缝的自追踪。值得注意的是,自追踪为双向追踪,则能弥补步骤五-6中跳过的一系列点。执行完自追踪后,并更新当前点q为q1执行步骤五-3。如果不满足条件,则执行步骤五-9。
步骤五-9: 标记该一系列潜在裂缝像素点为裂缝像素点。由于裂缝在此步标记不是很严格,则在该点出不计算裂缝的宽度。
步骤五-10: 判断需要检测的裂缝是否检测完全。如果两种子点间的裂缝检测还未完毕,则更新当前点q为q1执行步骤五-3。如果检测完毕,则最终识别出整个裂缝。
步骤六:判断种子点是否检测完毕。如果为否,则令 ,再次执行步骤五;如果判断结果为是,则提取一条完整的裂缝,并得到裂缝的宽度。
基于半交互式的裂缝检测方法,依赖于用户点取的种子点和裂缝的自身走势来检测裂缝并计算其宽度。一方面,用户点取的一系列种子点能保证裂缝检测的连续性;另一方面,根据Hessian矩阵的特征向量来刻画裂缝的走势,并根据此趋势来提取裂缝能保证裂缝检测的准确性。本技术的创新之处表现为以下两方面:第一,本技术将用户的半交互式与根据裂缝的走势进行完美的结合,不仅能对抗多变性背景的干扰,并能广泛的应用于各种复杂的应用场景,而且能保证裂缝检测的高精度需求。第二,本技术与之前相关工作类似,也用到了Hessian矩阵刻画裂缝的走势,但是不同之处在于本技术提出了切线方向相似性度量以及双向原则来扩展裂缝,而不是在当前点的切线方向上单向的盲目扩展到下一个点;根据梯度信息和方向信息准则而不是通过极值点寻找边界,保证了边界的准确性,因为微分方法受噪声影响较大而通常找到局部极值点而带来检测偏差;另外,在裂缝自追踪断点出,提出一系列准则进行潜在裂缝点的选取,并保证自追踪的继续,从而实现裂缝检测的完整性和准确性。此技术乃整个检测流程的核心所在。具体的优点说明如下:
-
检测精度高。本技术基于裂缝的走势追踪整个裂缝,能有效消除噪声、光照,背景复杂等不利因素的影响;并且根据梯度信息和方向信息能准则提取整个裂缝像素,潜在裂缝点的选取保证裂缝自追踪的完整性。之前相关工作在裂缝检测中边界出现较大偏差,并且在复杂的应用场景下检测的断断续续;而本技术不仅能准确且完整的检测整个裂缝,并且能达到很高的检测准确率。
-
鲁棒性好。本技术基于半交互式,对图像成像质量要求低,对图像采集环境具有自适应能力;具有普适性,适用于隧道裂缝,路面裂缝,墙壁裂缝,板材裂缝等,一些检测结果如下图所示。虽然本技术只应用到了上述裂缝检测场景,很明显该技术同样适用于其它目标具备相似特征的场合,比如医学领域中毛细血管的检测等。
代码托管在Github上,C++版本:https://github.com/andrewganjinrui/CrackInspection_C;Matlab版本:https://github.com/andrewganjinrui/CrackInspection_Matlab。特别注意,matlab版本有交互式操作,首先用鼠标标定一个包含裂缝的兴趣框(主要是提高计算效率);然后用鼠标点击裂缝的一些关键拐点,点数可在程序中更改,点击完毕裂缝的检测结果就会呈现出来。



