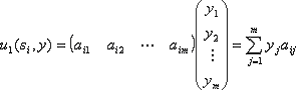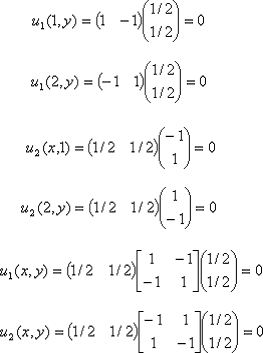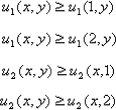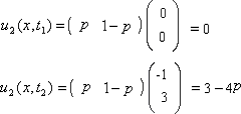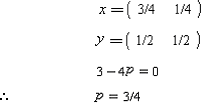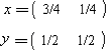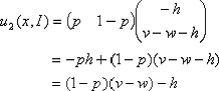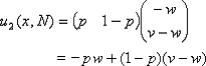混合策略纳什均衡计算

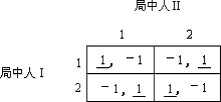
为了了解博弈论中引入“混合策略”概念的动机，我们来看用“划线法”对相当简单的“猜谜博弈”求解的结果，其结果如图8.3.1所示。

    求解的答案是，在纯策略意义下“猜谜博弈”无解，即不存在在纯策略意义下的纳什均衡，也就是说，这个博弈得不到一个平衡稳定的结局。但经验告诉我们，两个儿童玩这样的猜谜游戏，一局难定胜负，一次又一次地玩下去，随机地出一个手指，或者两个手指，多次以后，基本胜负各半，也就是有了一个平衡的结果。这个启示是，若一个博弈在纯策略意义下没有平衡的结局，但两个局中人各自将自己的全部策略随机地组织起来，且可能得到平衡的结局，换言之，在概率策略的意义下可能存在纳什均衡。正是这样的思考，引发了“混合策略”的概念。

一、混合策略

    1．混合策略的定义
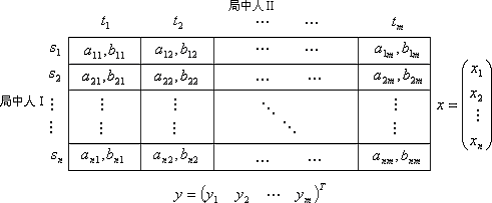
    设  Ⅰ与Ⅱ是一个博弈的两个局中人。他们的纯策略集(c8.2)分别记为：

        S={s₁,s₂,…s_n}和T={t₁,t₂, …t_m}        （8.3.1）

    x与y是两个概率向量，即：

        x=(x₁,x₂, …x_n)T；xi≥0（i=1,2, …n）;∑x_i = 1
        y=(y₁,y₂, …y_m)T；yj≥0（j=1,2, …m）;∑y_j = 1

    若 x表示对局中人Ⅰ的纯策略集S的全体策略的一种概率选择；y表示对局中人Ⅱ的纯策略集T的全体策略的一种概率配置，即：

        Ⅰ 以概率x₁选择策略s₁，以概率x₂选择策略s₂，……以概率x_n选择策略s_n。
        Ⅱ 以概率y₁选择策略t₁，以概率y₂选择策略t₂，……以概率y_m选择策略t_m。

    则  称x为局中人Ⅰ的混合策略；称y为局中人Ⅱ的混合策略。

    混合策略的实践意义是表示局中人对各个纯策略的偏好程度，或是对多次博弈达到均衡结局的各个纯策略选择的概率估计，因此体现了主观概率的意义。

    2．混合策略集

    根据混合策略的定义，易见，纯策略可视为特殊的混合策略。例如局中人Ⅰ的一个纯策略策略s_i∈S 就是特殊的混合策略x' ：此概率向量的分量取值为：

        x'_i=1 ，x'_j=0        （j≠i）

也就是Ⅰ选择策略s₁的概率为0（不妨设i≠1），……选择策略s_i的概率为1，……选择策略s_n的概率为0（不妨设i≠n）。有了这个见解，后文中，我们将记：

        X={x∈R_n| x=(x₁,x₂, …x_n)T；x_i≥0（i=1,2, …n）; ∑x_i = 1}； (8.3.2)
        Y={y∈R_m| y=(y₁,y₂, …y_m)T；y_j≥0（j=1,2, …m）;∑y_j = 1}。 (8.3.3)

并称：X为局中人Ⅰ的策略集或混合策略集。Y为局中人Ⅱ的策略集或混合策略集。以及(x, y) ∈X×Y为博弈的混合策略结局。

    注意到纯策略集S是一个有限集，由它生成的凸集，也就是单纯形（参阅第二章有关内容）可表示为：

    可见，混合策略集X与纯策略集S生成的凸集（单纯形）1－1对应（在数学上称为同构），因此可以把混合策略集X“看成”由纯策略集S拓展的凸集（单纯形），而且集S是集X的极点子集。同理可以把混合策略集Y“看成”由纯策略集T拓展的凸集（单纯形），而且集T是集Y的极点子集。按照这样的理解，就不难把握混合策略的概念，即每一个混合策略x表示了由全部纯策略s_i∈S以凸组合方式产生的一个策略。

    3．混合策略结局的盈利函数

    设  博弈的局中人Ⅰ与Ⅱ各自的纯策略集S和T，以及各自的混合策略集X、Y分别由式（8.3.1）、式（8.3.2）和式（8.3.3）定义。博弈的盈利矩阵模型为：

我们定义局中人Ⅰ的盈利矩阵为：

定义局中人Ⅱ的盈利矩阵为：

    则  定义混合策略结局的盈利函数如下：

    (1) 任取s_i∈S，任取y∈Y，定义结局（s_i, y）的盈利函数为：

        （8.3.4）

    (2) 任取t_j∈T，任取x∈X，定义结局（x, t_j）的盈利函数为：

        (8.3.5)

    (3) 任取x∈X，任取y∈y，定义结局（x, y）的盈利函数为：

(8.3.6)

(8.3.7)

    将式(8.3.6)给出的u₁(x,y)的定义与(8.3.4)给出的u1(s_i,y)的定义作联系分析，以及将式(8.3.7)给出的u₂(x,y)的定义与(8.3.5)给出的u₂(x,t_j)的定义作联系分析，容易得出u₁(x,y)以及u₂(x,y)有下列等价的表达式：

        (8.3.9)

        (8.3.10)

二、混合策略的纳什均衡

    （一）混合策略纳什均衡的概念

    1、混合策略纳什均衡的定义
    设  博弈的局中人Ⅰ与Ⅱ各自的纯策略集S和T，以及各自的混合策略集X、Y分别由式（8.3.1）、式（8.3.2）和式（8.3.3）定义。
    若  一个混合策略的结局(x, y)∈X×Y满足下列条件：

    （1）         (8.3.11)

    （2）         (8.3.12)

    则  称混合策略的结局(x, y)是纳什均衡。

    2、混合策略纳什均衡的含义
    因为可以把混合策略集X“看成”以纯策略集S为极点子集而拓展的凸集（单纯形）。因此根据定义在凸集上的函数（称为凸函数）的性质，可以证明,若式（8.3.11）成立，则下式也必然成立：

        (8.3.13)

类似地，若式（8.3.12）成立，则下式也必然成立：

        (8.3.14)

    式（8.3.13）及式（8.3.14）表示。x是局中人Ⅰ对局中人Ⅱ选择了策略y后的最优策略（条件盈利最大），以及y是局中人Ⅱ对局中人Ⅰ的选择了策略x后的最优策略（条件盈利最大）。

    由于在博弈中局中人Ⅰ和局中人Ⅱ都选择“理性”行动，这样双方的博弈将在结局（x, y）下达到均衡状态。

    [例8.3.1]  验证x=(1/2, 1/2)^T , y=(1/2, 1/2)^T 构成的混合策略结局（x, y）是“猜谜博弈”的纳什均衡。

    解  “猜谜博弈”的模型是：

纯策略集S={1，2}（即{出一指，出两指}），纯策略集T={1，2}。由式（8.3.4）、式（8.3.5）、式（8.3.6）和式（8.3.7）。

因此下列不等式成立

由式（8.3.8）和式（8.3.8）知，混合结局（x, y）是“猜谜博弈”的纳什均衡。

    （二）”2策略博弈“的求纳什均衡的方法

    [定理8.3.1] 
    若  博弈的局中人Ⅰ与Ⅱ各自的纯策略集S和T都是2策略集：

        S={s₁,s₂ }和T={t₁,t₂ }

    则  混合策略结局（x, y）是纳什均衡的充要条件是：

        (8.1.15)

        (8.1.16)

    证明  可设：

    先证必要性，设（x, y）是纳什均衡。由式 (8.3.9)

由纳什均衡的含义，混合策略x是局中人Ⅰ在预测对局中人Ⅱ选择y 下的最优策略，因此由：

即

    再正充分性，设u1(s₁,y)=u1(s₂,y),则

同理可得：

从而由纳什均衡的定义式（8.3.11）和式（8.3.12）可知（x, y）是纳什均衡。

    [例8.3.2] 求图8.3.2给出的博弈的纳什均衡。

    解  由式（8.3.4）

由式（8.3.15 ）的要求解

               2q-1=0
    ∴         q=1/2

由式（8.3.5）

由式（8.3.16 ）的要求解

故求得纳什均衡

　

三、混合策略纳什均衡的两则应用

    我们介绍“监察博弈”和“共同投资博弈”来认识混合策略纳什均衡的典型应用

    （一）监察博弈

    1、监察博弈的模型
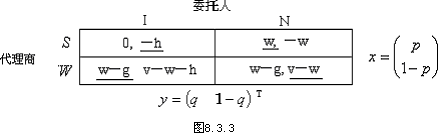
    代理商为委托人干活，有两个策略可供选择：工作（W）与偷懒（S）。假设工作使代
商花费g，由此获得委托人付给他的工资w（w>g是一个合理的假设，否则代理商没有任何工作积极性）。委托人在监督方面也有两个可供寻则的纯策略：检查（I）与不检查（N）。如果委托人检查需要费用h，以此代价换得代理商是否在偷懒的信息。一旦发现代理商偷懒，则扣除工资作为惩罚，若代理商工作而不偷懒，则将为委托人增加价值v的财产（显然v>w）。如果这些信息是共同知识，两个局中人进行完全信息静态博弈。进而, 不妨假设g>h>0，即抓住主要矛盾，忽视次要情况，以简便讨论。这个博弈的盈利矩阵如图8.3.3所示。

    2．求图监察博弈的纳什均衡，并求委托人应付给代理人的工资的参考值。
    （1）求图监察博弈的纳什均衡。
    首先用划线法试求纯策略纳什均衡，结果如图8.3.3所示，可见，监察博弈在不存在纯策略纳什均衡。下面依据定理8.3.1求混合策略纳什均衡。

由u₁(W,y)=u₁(S,y),得：

(1-q)w=w-g        (8.3.17)

    实际上（8.3.17）式左端是代理商偷懒时的期望盈利，而右端是代理商工作时的期望盈利。因此（8.3.17）式表示，在纳什均衡中委托人所取的混合策略y，必须使得代理商在工作或偷懒之间的选择由于平均盈利相等而表现出无所谓的态度。解（8.3.17）式，得：

q=g/w        (8.3.18)

再由

        (8.3.19)

        (8.3.20)

由u₂(x,I)=u₂(x,N)得：

        (8.3.21)

    类似地（8.3.21）式表示，在纳什均衡中代理商所取的混合策略x，必须使得委托人在选择检查还是不检查方面持无所谓的态度。解（8.3.21）式，得：

p=h/w        (8.3.22)

    综上所述，我们得到监察博弈的混合策略解，即混合策略纳什均衡：

((h/w,1-h/w),(g/w,1-g/w))

    （2）确定委托人应付给代理人的工资的参考值。

    由(8.3.10)式，以及(8.3.19)式和(8.3.20)式委托人的期望盈利是：

(8.3.23)

将p=h/w和q=g/w代入(8.3.23)式，即求得在纳什均衡时的委托人的期望盈利：

(8.3.23)

    可见在纳什均衡时的委托人的期望盈利与代理商为他增加的价值v、委托人的检查费用h以及委托人支付给代理商的工资w有关，一般地v与h可视作固定。对委托人而言，他应支付给代理商的工资，应该以期望盈利为最大为参考目标，从而由高等数学的极值定理，参考工资w应使下式成立：

可作为支付给委托人应支付给代理商的工资的参考值。

    （二）共同投资博弈

    1、共同投资博弈模型
    有两个投资者，共同投资一个较大的项目，他们可以获得较大的回报。但若他俩中有一人抽出资金用于一个小项目，抽出者尽管比投资较大项目时收益要小，但他肯定可以获得相应回报，然而他的这一做法将使较大项目陷于困境，会使另一投资者蒙受损失。是冒一定风险坚持投资于较大的项目，以获取较大的回报，还是抽回资金投资于小项目以图有个“旱涝保收”这就是“共同投资博弈”要解决的问题。图8.3.4给出了这个博弈的模型，其中的数据是假设的，但能刻画这个博弈的各种结局是的局中人的收益。模型中U表示局中人Ⅰ坚持投资大项目，D表示局中人Ⅰ抽回资金投资小项目；模型中L表示局中人Ⅱ坚持投资大项目，R表示局中人Ⅱ抽回资金投资小项目。

    （1）“有效”最优均衡
    用划线法求纯策略解，如图8.3.4所示。博弈存在两个纯策略均衡：（U，L）与（D，R）, 毫无疑问结局（U，L）是“有效”（经济学概念）的最优结局，因为（U，L）是在不损害他人的前提下，局中人将不可能再增加自己的利益，因此在经济上也是有效结果。

    （2）风险占优均衡
从风险占优的角度来考虑，对局中人Ⅰ来说，策略D比策略U更“安全”一些，因为局中人Ⅰ只要选择了D，不管局中人Ⅱ如何行动，局中人Ⅰ至少可以获得盈利7，或者更好一些（盈利8）。但倘若他取策略U，尽管他可能获得博弈的最高盈利9，然而也存在着落得一无所有的可能，即时，因此：

    风险占优要考虑的是：局中人Ⅱ取R的可能性有多大时，局中人Ⅰ只要选择 D的盈利会大于选择U的盈利。

    我们可设局中人Ⅱ取R概率为y，这时局中人Ⅰ取U时的期望盈利为：

u₁(U,y)=9(1-y)+0*y=9-9y

而局中人Ⅰ取策略D时的期望盈利为：

u₁(D,y)=8(1-y)+7y=8-y

解不等式：

9-9y<8-y

得y≥1/8。

这表明，如果局中人Ⅰ预测到局中人Ⅱ取策略R的概率大于1/8的话，从期望盈利考虑，局中人Ⅰ应采取D。注意到盈利矩阵关于两个局中人是对称的，同样的讨论告知，如果局中人Ⅱ预测到局中人Ⅰ取策略D的概率大于1/8的话，从期望盈利考虑，局中人Ⅰ应采取R。1/8是个小概率，因此一般来说，从风险占优角度，（D，R）优于（U，L）。