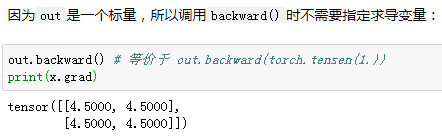
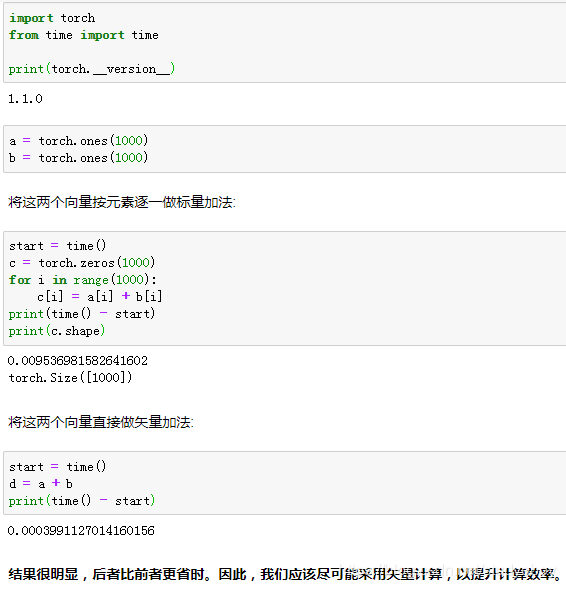
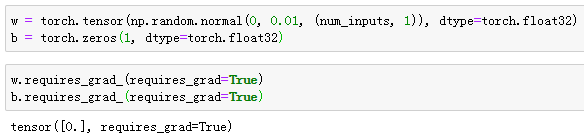
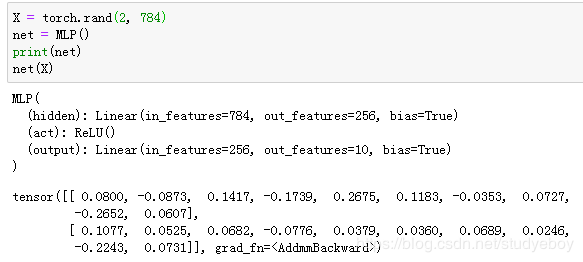
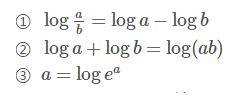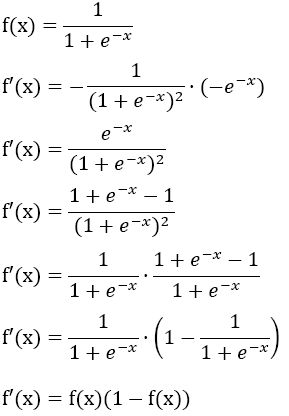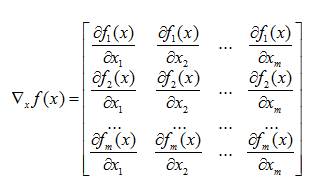《动手学深度学习》—学习笔记
文章目录
- 深度学习简介
- 起源
- 特点
- 小结
- 预备知识
- 获取和运行本书的代码
- pytorch环境安装
- 方式一
- 方式二
- 数据操作
- 创建
- 运算
- 广播机制
- 索引
- 运算的内存开销
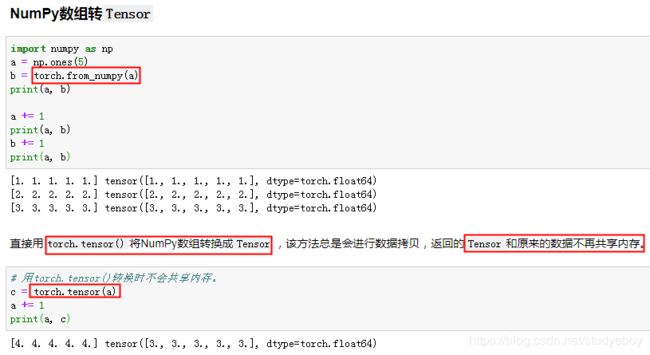
- NDArray和NumPy相互变换
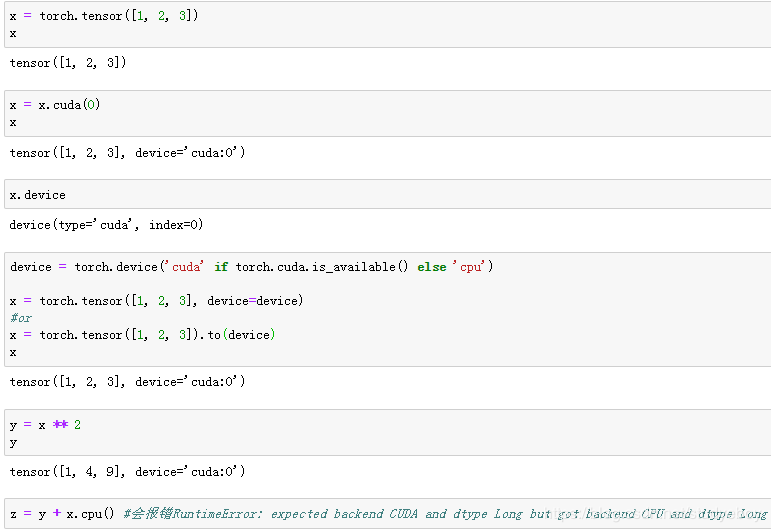
- Tensor on GPU(PyTorch)
- 自动求梯度
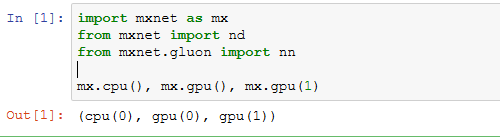
- MXNet
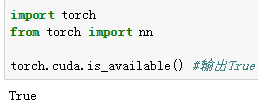
- PyTorch
- 查阅文档
- 深度学习基础
- 线性回归
- 线性回归的基本要素
- 模型
- 模型训练
- 模型预测
- 线性回归的表示方法
- 神经网络图
- 矢量计算表达式
- 小结
- 线性回归的从零开始实现
- 生成数据集
- 读取数据
- 初始化模型参数
- 定义模型
- 定义损失函数
- 定义优化算法
- 训练模型
- 小结
- 线性回归的简洁实现
- 生成数据集
- 读取数据集
- 模型定义
- 初始化模型参数
- 定义损失函数
- 定义优化算法
- 训练模型
- 小结
- softmax回归
- 分类问题
- softmax回归模型
- softmax计算
- 单样本分类的矢量计算表达式
- 小批量样本分类的矢量计算表达式
- 交叉熵损失函数
- 模型预测及评价(线性回归没有评价)
- 小结
- 图像分类数据集(Fashion-MNIST)
- 获取数据集
- 读取小批量
- 小结
- softmax回归的从零开始实现
- 获取和读取数据
- 初始化模型参数
- 实现softmax运算
- 定义模型
- 定义损失函数
- 计算分类准确率
- 训练模型
- 预测
- 小结
- softmax回归的简洁实现
- 获取和读取数据
- 定义和初始化模型
- softmax和交叉熵损失函数
- 定义优化算法
- 训练模型
- 小结
- 多层感知机
- 隐藏层
- 激活函数
- ReLU函数
- sigmoid函数
- tanh函数
- 多层感知机
- 小结
- 多层感知机的从零开始实现
- 获取和读取数据
- 定义模型参数
- 定义激活函数
- 定义模型
- 定义损失函数
- 训练模型
- 多层感知机的简洁实现
- 定义模型
- 读取数据并训练模型
- 模型选择、欠拟合和过拟合
- 训练误差和泛化误差
- 模型选择
- 验证数据集
- K折交叉验证
- 欠拟合和过拟合
- 模型复杂度
- 训练数据集大小
- 多项式函数拟合实验
- 生成数据集
- 定义、训练和测试模型
- 三阶多项式函数拟合(正常)
- 线性函数拟合(欠拟合)
- 训练样本不足(过拟合)
- 小结
- 权重衰减
- 方法
- 高维线性回归实验
- 从零开始实现
- 初始化模型参数
- 定义L2范数惩罚项
- 定义训练和测试
- 观察过拟合
- 使用权重衰减
- 简洁实现
- 小结
- 丢弃法
- 方法
- 从零开始实现
- 定义模型参数
- 定义模型
- 训练和测试模型
- 简洁实现
- 小结
- 正向传播、反向传播和计算图
- 正向传播
- 正向传播的计算图
- 反向传播
- 训练深度学习模型
- 小结
- 数值稳定性和模型初始化
- 衰减和爆炸
- 随机初始化模型参数
- MXNet的默认随机初始化
- Xavier随机初始化
- 小结
- 实战Kaggle比赛:房价预测
- Kaggle比赛
- 获取和读取数据
- 预处理数据
- 训练模型
- K折交叉验证
- 模型选择
- 预测并在Kaggle提交结果
- 小结
- 深度学习计算
- 模型构造
- 继承Block类来构造模型
- Sequential类继承自Block类
- 构造复杂的模型
- 小结
- 模型参数的访问、初始化和共享
- 访问模型参数
- 初始化模型参数
- 自定义初始化方法
- 共享模型参数
- 小结
- 模型参数的延后初始化
- 延后初始化
- 避免延后初始化
- 小结
- 自定义层
- 不含模型参数的自定义层
- 含模型参数的自定义层
- 小结
- 读取和存储
- 读写NDArray
- 读写Gluon模型的参数
- 小结
- GPU计算
- 计算设备
- NDArray的GPU计算
- GPU 上的存储
- GPU上的计算
- Tensor的GPU计算(PyTorch)
- Gluon的GPU计算
- 模型的GPU计算(PyTorch)
- 小结
- 卷积神经网络
- 二维卷积层
- 二维互相关运算
- 二维卷积层
- 图像中物体边缘检测
- 通过数据学习核数组
- 互相关运算和卷积运算
- 特征图和感受野
- 小结
- 填充和步幅
- 填充
- 步幅
- 小结
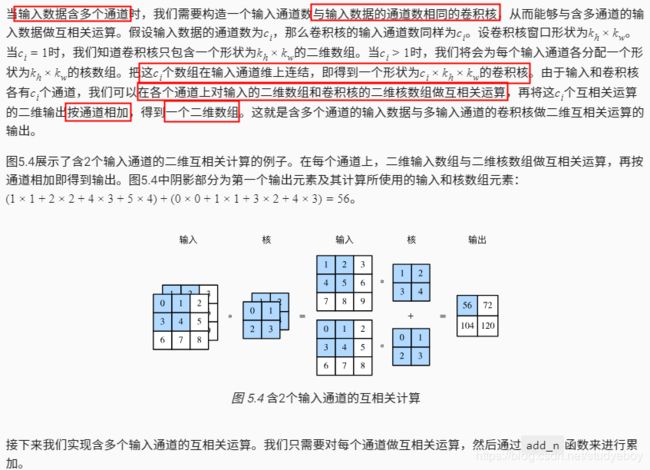
- 多输入通道和多输出通道
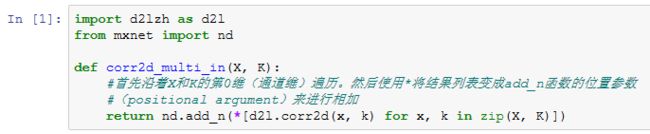
- 多输入通道
- 多输出通道
- 1x1卷积层
- 小结
- 池化层
- 二维最大池化层和平均池化层
- 填充和步幅
- 多通道
- 小结
- 卷积神经网络(LeNet)
- LeNet模型
- 获取数据和训练模型
- 小结
- 深度卷积神经网络(AlexNet)
- 学习特征表示
- 缺失要素一:数据
- 缺失要素二:硬件
- AlexNet
- 读取数据
- 训练
- 小结
- 使用重复元素的网络(VGG)
- VGG块
- VGG网络
- 获取数据和训练模型
- 小结
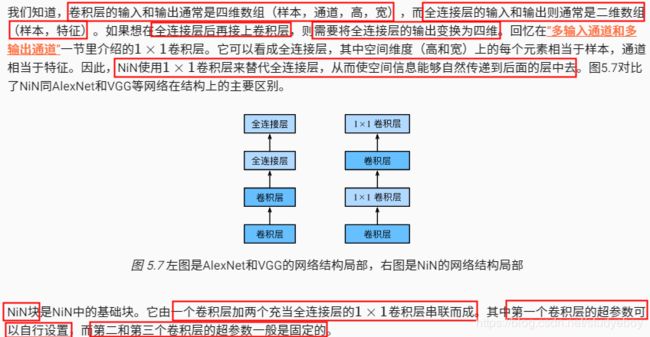
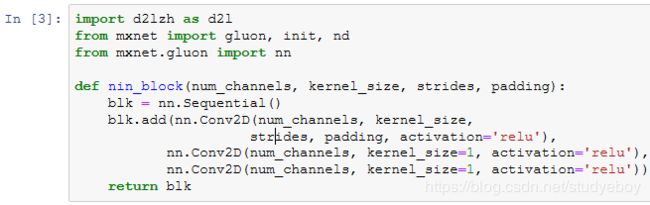
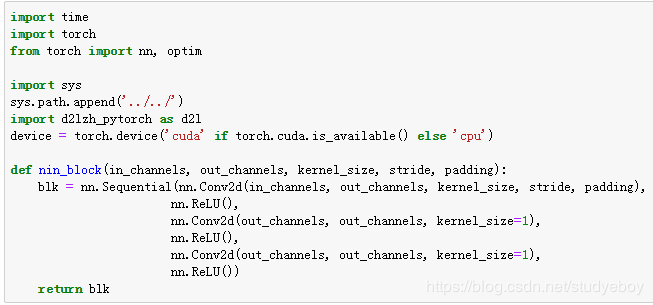
- 网络中的网络(NiN)
- NiN块
- NiN模型
- 获取数据和训练模型
- 小结
- 含并行连接的网络(GoogLeNet)
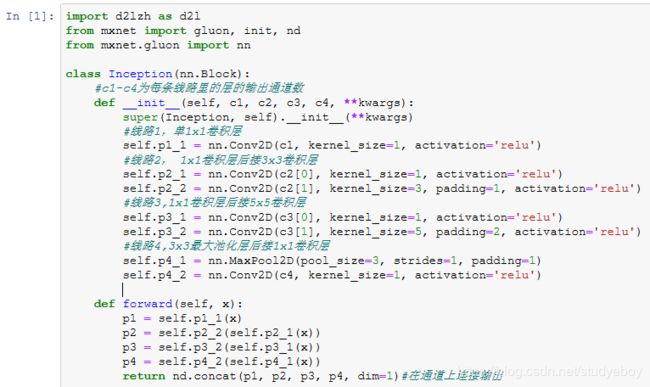
- Inception块
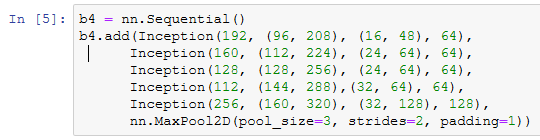
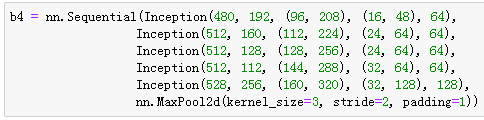
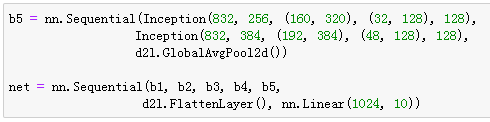
- GoogLeNet模型
- 获取数据和训练模型
- 小结
- 批量归一化
- 批量归一化层
- 对全连接层做批量归一化
- 对卷积层做批量归一化
- 预测时的批量归一化
- 从零开始实现
- 使用批量归一化层的LeNet
- 简洁实现
- 小结
- 残差网络(ResNet)
- 残差块
- ResNet模型
- 获取数据和训练模型
- 小结
- 稠密连接网络(DenseNet)
- 稠密块
- 过渡层
- DenseNet模型
- 获取数据并训练模型
- 小结
- 循环神经网络
- 语言模型
- 语言模型的计算
- n元语法
- 小结
- 循环神经网络
- 不含隐藏状态的神经网络
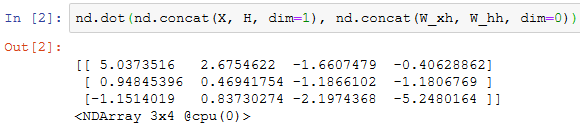
- 含隐藏状态的循环神经网络
- 应用:基于字符级循环神经网络的语言模型
- 小结
- 语言模型数据集(周杰伦专辑歌词)
- 读取数据集
- 建立字符索引
- 时序数据的采样
- 随机采样
- 相邻采样
- 小结
- 循环神经网络的从零开始实现
- one-hot向量
- 初始化模型参数
- 定义模型
- 定义预测函数
- 裁剪梯度
- 困惑度
- 定义模型训练函数
- 训练模型并创作歌词
- 小结
- 循环神经网络的简洁实现
- 定义模型
- 训练模型
- 小结
- 通过时间反向传播
- 定义模型
- 模型计算图
- 方法
- 小结
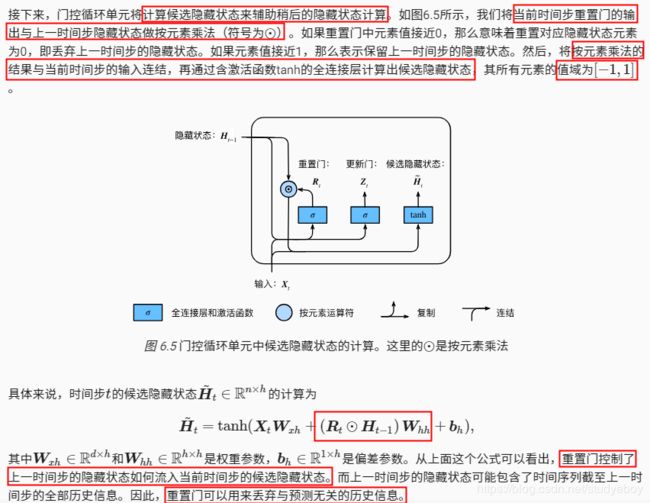
- 门控循环单元(GRU)
- 门控循环单元
- 重置门和更新门
- 候选隐藏状态
- 隐藏状态
- 读取数据集
- 从零开始实现
- 初始化模型参数
- 定义模型
- 训练模型并创作歌词
- 简洁实现
- 小结
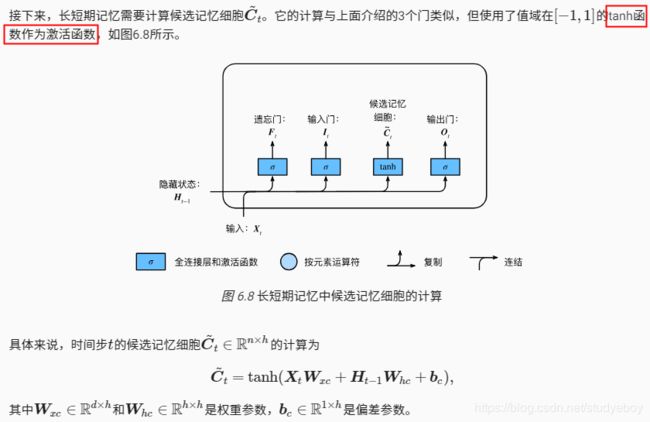
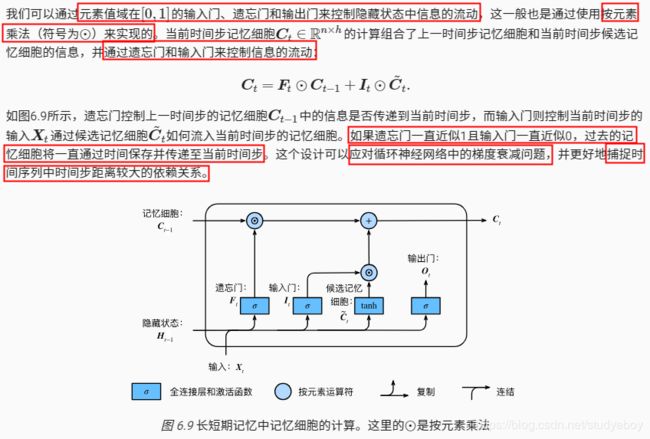
- 长短期记忆(LSTM)
- 长短期记忆
- 输入门、遗忘门、和输出门
- 候选记忆细胞
- 记忆细胞
- 隐藏状态
- 读取数据集
- 从零开始实现
- 初始化模型参数
- 定义模型
- 训练模型并创作歌词
- 简洁实现
- 小结
- 深度循环神经网络
- 小结
- 双向循环神经网络
- 小结
- 优化算法
- 优化与深度学习
- 优化与深度学习的关系
- 优化在深度学习中的挑战
- 局部最小值
- 鞍点
- 小结
- 梯度下降和随机梯度下降
- 一维梯度下降
- 学习率
- 多维梯度下降
- 随机梯度下降
- 小结
- 小批量随机梯度下降
- 读取数据
- 从零开始实现
- 简洁实现
- 小结
- 动量法
- 梯度下降的问题
- 动量法
- 指数加权移动平均
- 由指数加权移动平均理解动量法
- 从零开始实现
- 简洁实现
- 小结
- AdaGrad算法
- 算法
- 特点
- 从零开始实现
- 简洁实现
- 小结
- RMSProp算法
- 算法
- 从零开始实现
- 简洁实现
- 小结
- AdaDelta算法
- 算法
- 从零开始实现
- 简洁实现
- 小结
- Adam算法
- 算法
- 从零开始实现
- 简洁实现
- 小结
- 计算性能
- 命令式和符号式混合编程
- 混合式编程取两者之长
- 使用HybridSequential类构造模型
- 计算性能
- 获取符号式程序
- 使用HybridBlock类构造模型
- 小结
- 异步计算
- MXNet中的异步计算
- 用同步函数让前端等待计算结果
- 使用异步计算提升计算性能
- 异步计算对内存的影响
- 小结
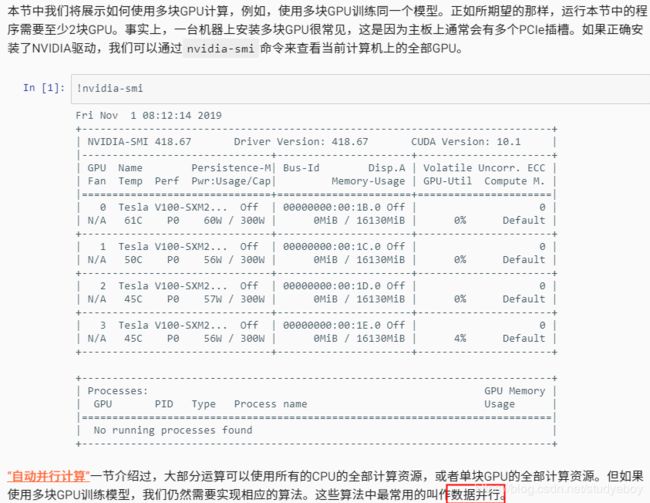
- 自动并行计算
- CPU和GPU的并行计算
- 计算和通信的并行计算
- 小结
- 多GPU计算
- 数据并行
- 定义模型
- 多GPU之间同步数据
- 单个小批量上的多GPU训练
- 定义训练函数
- 多GPU训练实验
- 小结
- 多GPU计算的简洁实现
- 多GPU上初始化模型参数
- 多GPU训练模型
- 小结
- 多GPU计算(PyTorch)
- 计算机视觉
- 图像增广
- 常用的图像增广方法
- 翻转和裁剪
- 变化颜色
- 叠加多个图像增广方法
- 使用图像增广训练模型
- 使用多GPU训练模型
- 小结
- 微调
- 热狗识别
- 获取数据集
- 定义和初始化模型
- 微调模型
- 小结
- 目标检测和边界框
- 边界框
- 小结
- 锚框
- 生成多个锚框
- 交并比
- 标注训练集的锚框
- 输出预测边界框
- 小结
- 多尺度目标检测
- 小结
- 目标检测数据集(皮卡丘)
- 下载数据集
- 读取数据集
- 图示数据
- 小结
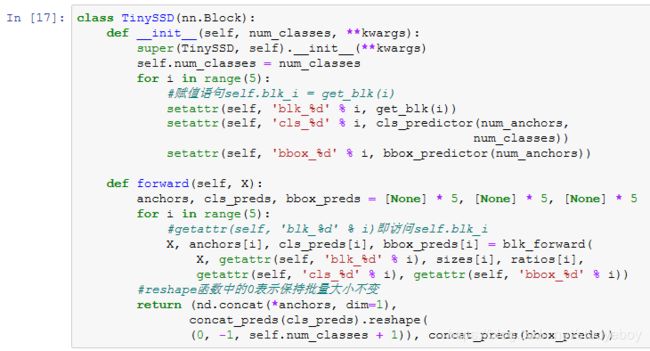
- 单发多框检测(SSD)
- 模型
- 类别预测层
- 边界框预测层
- 连接多尺度的预测
- 高和宽减半块
- 基础网络块
- 完整的模型
- 训练模型
- 读取数据集和初始化
- 定义损失函数和评价函数
- 训练模型
- 预测
- 小结
- 区域卷积神经网络(R-CNN)系列
- R-CNN
- Fast R-CNN
- Faster R-CNN
- Mask R-CNN
- 小结
- 语义分割和数据集
- 图像分割和实例分割
- Pascal VOC2012语义分割数据集
- 预处理数据
- 自定义语义分割数据集
- 读取数据集
- 小结
- 全卷积网络(FCN)
- 转置卷积层
- 构造模型
- 初始化转置卷积层
- 读取数据集
- 训练模型
- 预测像素类别
- 小结
- 样式迁移
- 方法
- 读取内容图像和样式图像
- 预处理后处理图像
- 抽取特征
- 定义损失函数
- 内容损失
- 样式损失
- 总变差损失
- 损失函数
- 创建和初始化合成图像
- 训练
- 小结
- 实战Kaggle比赛:图像分类(CIFAR-10)
- 获取和整理数据集
- 下载数据集
- 解压数据集
- 整理数据集
- 图像增广
- 读取数据集
- 定义模型
- 定义训练函数
- 训练并验证模型
- 对测试集分类并在Kaggle提交结果
- 小结
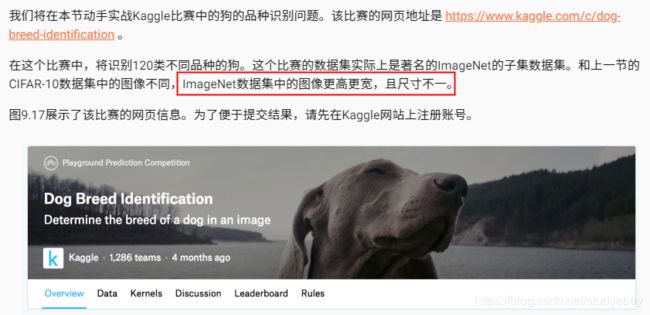
- 实战Kaggle比赛:狗的品种识别(ImageNet Dogs)
- 获取和整理数据集
- 下载数据集
- 整理数据集
- 图像增广
- 读取数据集
- 定义模型
- 定义训练函数
- 训练并验证模型
- 对测试集分类并在Kaggle提交结果
- 小结
- 自然语言处理
- 词嵌入(word2vec)
- 为何不采用one-hot向量
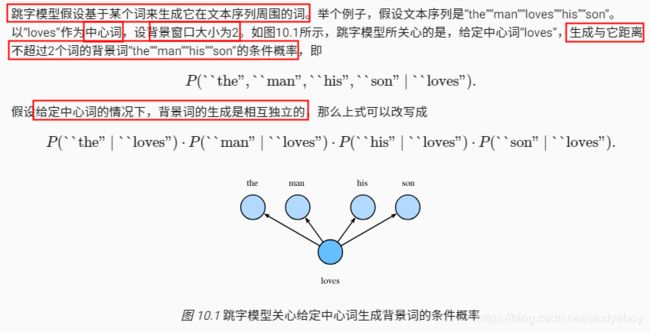
- 跳字模型
- 训练跳字模型
- 连续词袋模型
- 训练连续词袋模型
- 小结
- 近似训练
- 负采样
- 层序softmax
- 小结
- word2vec实现
- 处理数据集
- 建立词语索引
- 二次采样
- 提取中心词和背景词
- 负采样
- 读取数据
- 跳字模型
- 嵌入层
- 小批量乘法
- 跳字模型前向计算
- 训练模型
- 二元交叉熵损失函数
- 初始化模型参数
- 定义训练函数
- 应用词嵌入模型
- 小结
- 子词嵌入(fastText)
- 小结
- 全局向量的词嵌入(GloVe)
- GLoVe模型
- 从条件概率比值理解GloVe模型
- 小结
- 求近义词和类比词
- 使用预训练的词向量
- 应用预训练的词向量
- 求近义词
- 求类比词
- 小结
- 文本情感分类:使用循环神经网络
- 文本情感分类数据
- 读取数据
- 预处理数据
- 创建数据迭代器
- 使用循环神经网络的模型
- 加载预训练的词向量
- 训练并评价模型
- 小结
- 文本感情分类:使用卷积神经网络(textCNN)
- 一维卷积层
- 时序最大池化层
- 读取和预处理IMDb数据集
- textCNN模型
- 加载预训练的词向量
- 训练并评价模型
- 小结
- 编码器-解码器(seq2seq)
- 编码器
- 解码器
- 训练模型
- 小结
- 预测不定长序列的方法
- 贪婪搜索
- 穷举搜索
- 束搜索
- 小结
- 注意力机制
- 计算背景变量
- 矢量化计算
- 更新隐藏层状态
- 发展
- 小结
- 机器翻译
- 读取和预处理数据
- 含注意力机制的编码器-解码器
- 编码器
- 注意力机制
- 含注意力机制的解码器
- 训练模型
- 预测不定长的序列
- 评价翻译结果
- 小结
- 附录
- 主要符号一览
- 数学基础
- 线性代数
- 微分
-
在线学习网址:
https://zh.d2l.ai/ -
GitHub:
d2l-zh(中文版)
d2l-en(英文版) -
代码
代码是基于Apache MXNet实现,MXNet是一个开源的深度学习框架。它是AWS(亚马逊云计算服务)首选的深度学习框架,也被众多的学校和公司使用。 -
Pytorch 版本
Dive-into-DL-PyTorch
《动手学深度学习》(PyTorch版) -
TensorFlow 版本
Dive-into-DL-TensorFlow2.0
《动手学深度学习》(TF2.0版)
深度学习简介
机器学习是一门讨论各式各样的适用于不同问题的函数形式,以及如何使用数据来有效的获取函数参数具体值的学科。深度学习是指机器学习中的一类函数,他们的形式通常为多层神经网络。深度学习已逐渐成为处理图像、文本语料和声音信号等复杂高维数据的主要方法。
起源
虽然深度学习似乎是近几年刚兴起的名词,但是它所基于的神经网络模型和用数据编程的核心思想已经被研究了数百年。实际上,数据分析正是大部分自然科学的本质,我们希望从日常的观察中提取规则,并找寻不确定性。
特点
机器学习研究如何使计算机系统利用经验改善性能。它是人工智能领域的分支,也是实现人工智能的一种手段。在机器学习的众多研究方法中,表征学习关注如何自动找出表示数据的合适方式,以便更好的将输入变换为正确的输出,而《动手学深度学习》重点探讨的深度学习是具有多级表示的表征学习方法。在每一级(从原始数据开始),深度学习通过简单的函数将该级的表示变换为更高级的表示。因此,深度学习模型也可以看作是由许多简单函数复合而成的函数。当这些复合的函数足够多时,深度学习模型就可以表示非常复杂的变换。
深度学习可以逐级表示越来越抽象的概念或模式。以图像为例,它的输入是一堆元素像素值。深度学习模型中,图像可以逐级表示为特定位置和角度的边缘、由边缘组合得出的花纹、由多种花纹进一步汇合得到的特定部位的模式等。最终,模型能够较容易根据更高级的表示完成给定的任务,如识别图像中的物体。值得一提的是,作为表征学习的一种,深度学习将自动找出每一级表示数据的合适方式。
因此,深度学习的一个外在特点是端到端的训练。也就是说,并不是将单独调试的部分拼凑起来组成一个系统,而是将整个系统组建好之后一起训练。比如说,计算机视觉科学家之前曾一度将特征抽取与机器学习模型的构建分开处理,像是Canny边缘探测和SIFT特征提取曾占据统治性地位达10年以上,但这也就是人类能找到的最好的方法了。当深度学习进入这个领域,这些特征提取方法就被性能更强的自动优化的逐级过滤器替代了。
相似地,在自然语言处理领域,词袋模型多年来都被认为是不二之选。词袋模型是将一个句子映射到一个词频向量的模型,但这样的做法完全忽视了单词的排列顺序或者句中的标点符号。不幸的是,我们也没有能力来手工抽取更好的特征。但是自动化的算法反而可以从所有可能的特征中搜寻最好的那个,这也带来了极大的进步。例如,语义相关的词嵌入能够在向量空间中完成如下推理:“柏林-德国+中国=北京”,可以看出,这些都是端到端训练整个系统带来的效果。
除端到端的训练以外,我们也正在经历从含参数统计模型转向完全无参数的模型。当数据非常稀缺时,需要通过简化对现实的假设来得到实用的模型。当数据充足时,可以用能更好的拟合现实的无参数模型来替代这些含参数模型。这也使我们可以得到更精确的模型,尽管需要牺牲一些可解释性。
相对其它经典的机器学习方法而言,深度学习的不同在于:对非最优解的包容、对非凸非线性优化的使用,以及勇于尝试没有被证明过的方法。这种在处理统计问题上的新经验主义吸引了大量人才的涌入,使得大量实际问题有了更好的解决方案。尽管大部分情况下需要为深度学习修改甚至重新发明已经在数十年的工具,但是这绝对是一件非常有意义并令人兴奋的事。
小结
- 机器学习研究如何使计算机系统利用经验改善性能。它是人工智能领域的分支,也是实现人工智能的一种手段。
- 作为机器学习的一类,表征学习关注如何自动找出表示数据的合适方式。
- 深度学习是具有多级表示的表征学习方法。它可以逐级表示越来越抽象的概念或模式。
- 深度学习所基于的神经网络模型和用数据编程的核心思想实际上已经被研究了数百年。
- 深度学习已经逐渐演变成了一个工程师和科学家皆可使用的普适工具。
预备知识
获取和运行本书的代码
- 下载Miniconda,它是一个sh文件。
- 进入下载目录,执行sh文件。安装时会显示使用条款,按“↓”继续阅读,按“Q”退出阅读。之后需要回答下面几个问题,回答yes,并给出安装路径
/mnt/disk2/xxx/smb-share/soft。
sh Miniconda3-latest-Linux-x86_64.sh
- 让conda生效,执行
source ~/.bashrc。
source ~/.bashrc
- 下载代码压缩包,解压后进入文件夹。
mkdir d2l-zh && cd d2l-zh
curl https://zh.d2l.ai/d2l-zh-1.0.zip -o d2l-zh.zip
unzip d2l-zh.zip && rm d2l-zh.zip
- 使用conda创建虚拟(运行)环境。conda和pip默认使用国外站点来下载软件,配置国内镜像来加速下载。
# 配置清华PyPI镜像(如无法运行,将pip版本升级到>=10.0.0)
pip config set global.index-url https://pypi.tuna.tsinghua.edu.cn/simple
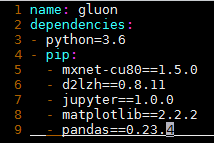
- 使用conda创建虚拟环境并安装本书需要的软件。这里environment.yml是放置在代码压缩包中的文件。
conda env create -f environment.yml
- 激活之前创建的环境。激活该环境是能够运行本书的代码的前提。如需退出虚拟环境,可使用命令conda deactivate(若conda版本低于4.4,使用命令deactivate)。
conda activate gluon # 若conda版本低于4.4,使用命令activate gluon
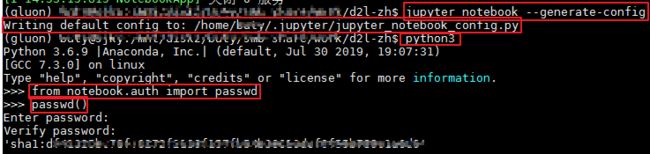
- 对jupyter notebook进行配置,使能够实现本地远程连接
jupyter notebook --generate-config
python3
from notebook.auth import passwd
passwd()
- 修改
~/.jupyter/jupyter_notebook_config.py
c.NotebookApp.ip='*' # 设置所有ip皆可访问
c.NotebookApp.password = u'' # 复制生成的秘钥
c.NotebookApp.open_browser = False # 禁止自动打开浏览器
c.NotebookApp.port = 8888 # 指定8888端口
c.NotebookApp.allow_remote_access = True
- 打开Jupyter记事本,通过服务器的ip + :8888即可远程访问
jupyter notebook
通过前面介绍的方式安装的MXNet只支持CPU计算。如果你的计算机上有NVIDIA显卡并安装了CUDA,建议使用GPU版的MXNet。
- 卸载CPU版的MXNet,如果没有安装虚拟环境,可以跳过此步。如果已安装虚拟环境,需要先激活该环境,再卸载CPU版本的MXNet。
- 退出虚拟环境
conda deactivate
- 修改根目录下的文件environment.yml,将里面的字符串“mxnet”替换成对应的GPU版本。例如,如果计算机上装的是8.0版本的CUDA,将该文件中的字符串“mxnet”改为“mxnet-cu80”。如果计算机上安装了其他版本的CUDA(如7.5、9.0、9.2等),对该文件中的字符串“mxnet”做类似修改(如改为“mxnet-cu75”“mxnet-cu90”“mxnet-cu92”等)。保存文件后退出。
- 更新虚拟环境
conda env update -f environment.yml
- 之后,我们只需要再激活安装环境就可以使用GPU版的MXNet运行本书中的代码了。需要提醒的是,如果之后下载了新代码,那么还需要重复这3步操作以使用GPU版的MXNet。
conda activate gluon
jupyter notebook
pytorch环境安装
方式一
- 官网给的安装命令,下载过慢,经常会出错。
#查看cuda版本
cat /usr/local/cuda/version.txt
#-n 参数指定虚拟环境名称
#conda install -n gluon pytorch==1.0.0 torchvision==0.2.1 cuda80 -c pytorch
conda install -n pytorch pytorch torchvision cudatoolkit=10.0 -c pytorch
- 从清华conda源地址下载,速度快。
conda config --add channels http://mirrors.tuna.tsinghua.edu.cn/anaconda/pkgs/free/
#-n 参数指定虚拟环境名称
#conda install -n gluon pytorch==1.0.0 torchvision==0.2.1 cuda80
conda install -n pytorch pytorch torchvision cudatoolkit=10.0
方式二
npm:Nodejs下的包管理器
webpack:通过CommonJS的语法把所有浏览器端需要发布的静态资源做相应的准备,比如资源的合并和打包。
vue-cli:用户生成Vue工程模板。(帮你快速开始一个vue的项目,也就是给你一套vue的结构,包含基础的依赖库,只需要npm install就可以安装。)
echo %PATH%
npm config set prefix "D:\software\nodejs\node_global"
npm config set cache "D:\software\nodejs\node_cache"
- 查看npm本地仓库是否修改
npm list -global
- 查看配置信息
npm config list
- 升级npm版本 ,-g参数指示安装到global目录下。
npm install npm -g
- 直接运行npm命令会报错,需要将D:\software\nodejs\node_global\node_modules目录添加到环境变量。添加后需要重新打开cmd让环境变量有效。
- 安装docsify-cli工具
npm i docsify-cli -g
- 将项目clone到本地
git clone https://github.com/ShusenTang/Dive-into-DL-PyTorch.git
cd Dive-into-DL-PyTorch
- 运行一个本地服务器,这样就可以很方便的在http://localhost:3000实时访问文档网页渲染效果。
docsify serve docs
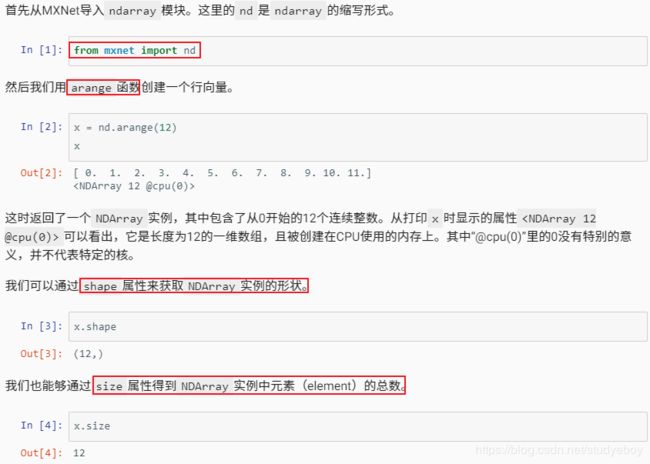
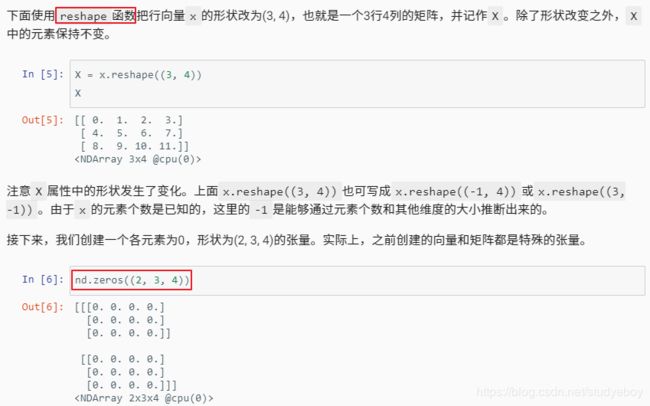
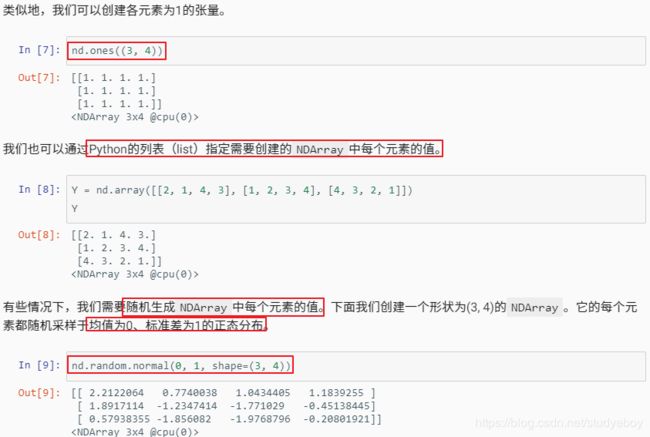
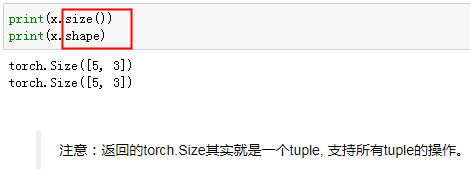
数据操作
创建
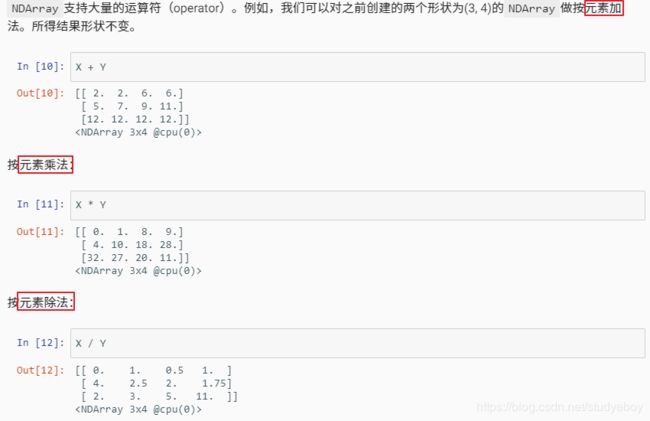
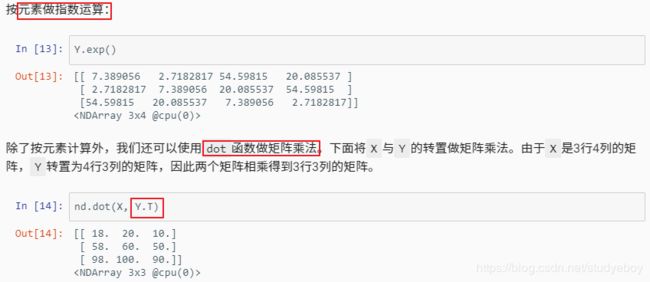
运算
广播机制
索引
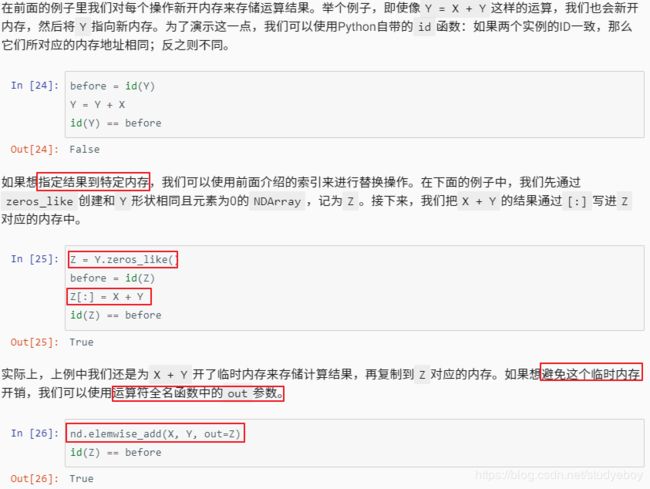
运算的内存开销
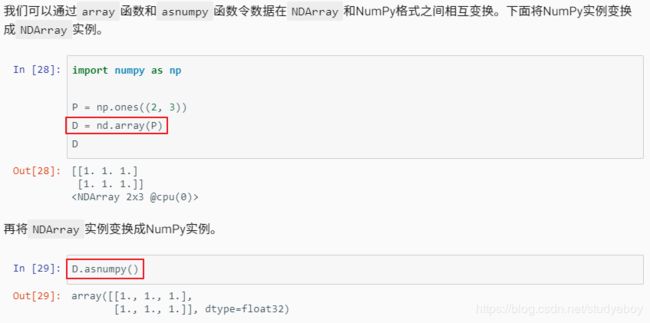
NDArray和NumPy相互变换
Tensor on GPU(PyTorch)
自动求梯度
MXNet
在深度学习中,我们经常需要对函数求梯度(gradient)。MXNe使用t提供的autograd模块来自动求梯度。
from mxnet import autograd, nd
PyTorch
查阅文档
深度学习基础
线性回归
![]()
线性回归的基本要素
模型
模型训练
模型预测
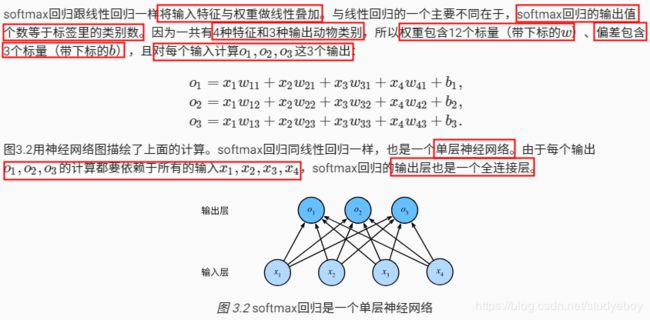
线性回归的表示方法
![]()
神经网络图
![]()
矢量计算表达式
小结
- 和大多数深度学习模型一样,对于现行回归这样一种单层神经网络,它的基本要素包括模型、训练数据、损失函数和优化算法。
- 既可以用神经网络图表示线性回归,又可以用矢量计算表示该模型。
- 应该尽可能采用矢量计算,以提升计算效率。
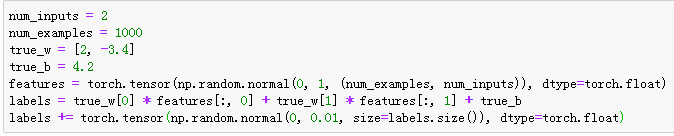
线性回归的从零开始实现
![]()
生成数据集
- MXNet


注意,features的每一行是一个长度为2的向量,而labels的每一行是一个长度为1的向量(标量)。

通过生成第二个特征features[:, 1]和标签 labels 的散点图,可以更直观地观察两者间的线性关系。
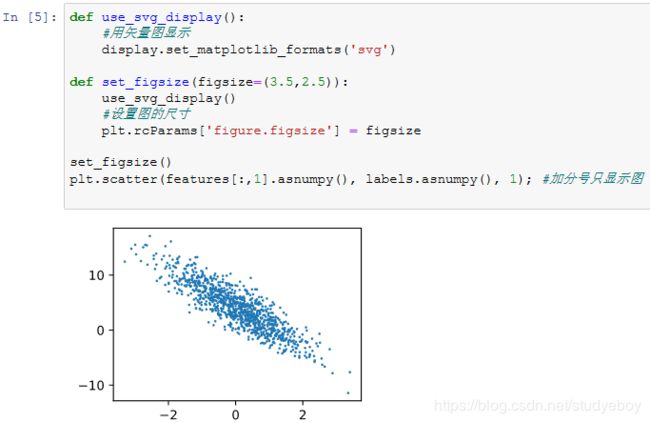
- PyTorch


读取数据
- MXNet
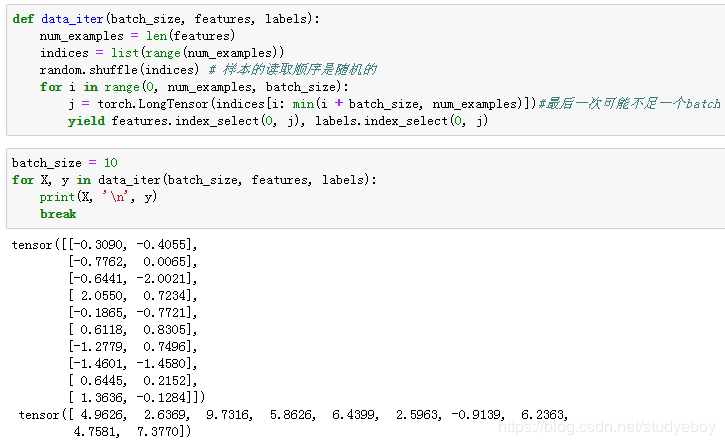
在训练模型的时候,我们需要遍历数据集并不断读取小批量数据样本。这里我们定义一个函数:它每次返回batch_size(批量大小)个随机样本的特征和标签。

让我们读取第一个小批量数据样本并打印。每个批量的特征形状为(10, 2),分别对应批量大小和输入个数;标签形状为批量大小。

- PyTorch
初始化模型参数
定义模型
- MXNet
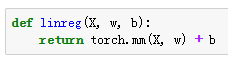
下面是线性回归的矢量计算表达式的实现。我们使用dot函数做矩阵乘法。

- PyTorch
定义损失函数
- MXNet
我们使用上一节描述的平方损失来定义线性回归的损失函数。在实现中,我们需要把真实值y变形成预测值y_hat的形状。以下函数返回的结果也将和y_hat的形状相同。

- PyTorch

定义优化算法
- MXNet
以下的sgd函数实现了上一节中介绍的小批量随机梯度下降算法。它通过不断迭代模型参数来优化损失函数。这里自动求梯度模块计算得来的梯度是一个批量样本的梯度和。我们将它除以批量大小来得到平均值。

- PyTorch

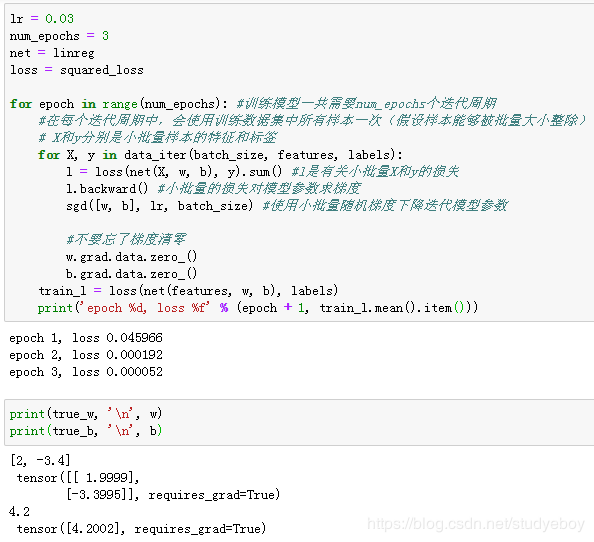
训练模型
小结
仅适用NDArray和autograd模块就可以很容易的实现一个模型。
线性回归的简洁实现
随着深度学习框架的发展,开发深度学习应用变得越来越便利。实践中,通常比上一节更简洁的代码来实现同样的模型。在本节中,将使用MXNet提供的Gluon接口更方便的实现线性回归的训练。
生成数据集
读取数据集
- MXNet
Gluon提供了data包来读取数据。由于data常用作变量名,将导入的data模块用添加了Gluon首字母的假名gdata代替。在每次迭代中,将随机读取包含10个数据样本的小批量。

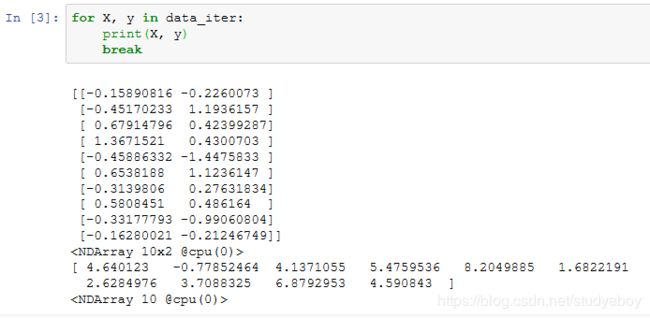
- PyTorch


模型定义
- MXNet
Gluon提供了大量预定义的层,这使我们只需要关注使用哪些层来构造模型。下面将介绍如何使用Gluon更简洁的定义线性回归。
首先,导入nn(neural networks,神经网络缩写)模块。该模块定义了大量神经网络的层。我们先定义一个模型变量net,它是一个Sequential实例。在Gluon中,Sequential实例可以看作是一个串联各个层的容器。在构造模型时,在该容器中依次添加层。当给定输入数据时,容器中的每一层将依次计算并将输出作为下一层的输入。

作为一个神经网络,线性回归输出层的神经元和输入层中各个输入完全连接。因此,线性回归的输出层又叫全连接层。在Gluon中,全连接层是一个Dense实例。定义该输出层个数为1。

在Gluon中,无需指定每个输入层的形状,例如线性回归的输入个数。当模型得到数据时,例如后面执行net(X)时,模型将自动推断出每一层的输入个数。 - PyTorcn


初始化模型参数
- MXNet
在使用net前,需要初始化模型参数,如线性回归模型中的权重和偏差。我们从MXNet导入init模块。该模块提供了模型参数初始化的各种方法。通过init.Normal(sigma=0.01)指定权重参数每个元素将在初始化时随机采样均值为0,标准差为0.01的正态分布。偏差参数默认会初始化为零。

- PyTorch
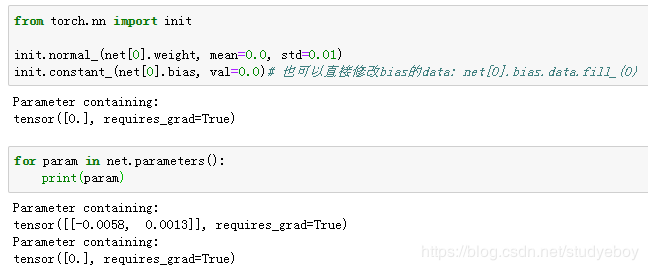
定义损失函数
定义优化算法
- MXNet
在导入Gluon后,创建一个Trainer实例,并制定学习率为0.03的小批量随机梯度下降(sgd)为优化算法。该优化算法将用来迭代net实例所有通过add函数嵌套的层所有包含的全部参数。这些参数可以通过collect_params函数获取。

- PyTorch
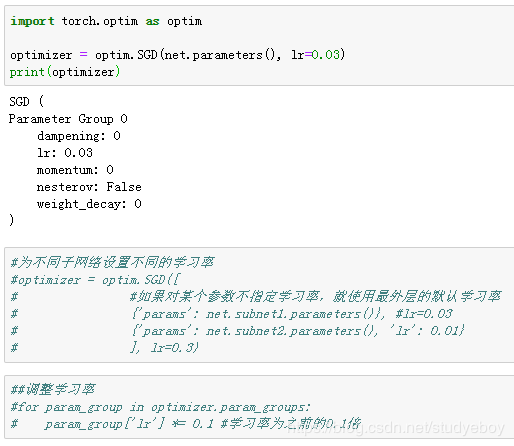
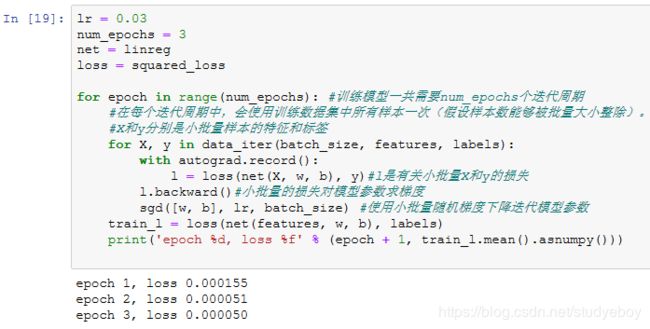
训练模型
- MXNet
在使用Gluon训练模型时,通过调用Trainer实例的step函数来迭代模型参数。由于变量l是长度为batch_size的一维NDArray,执行l.backward()等价于执行l.sum.backward()。按照小批量随机梯度下降的定义,在step函数中指明批量大小,从而对批量中样本梯度求平均。
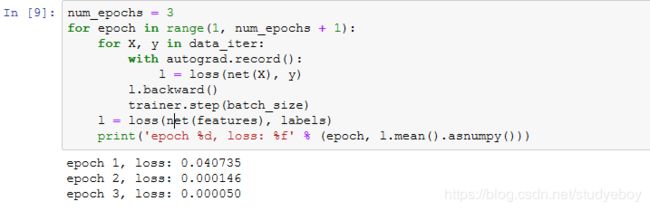
比较学到的模型参数和真实的模型参数。从net获取得需要的层,并访问其权重(weight)和偏差(bias)。学到的参数和真实的参数都很接近。


- PyTorch
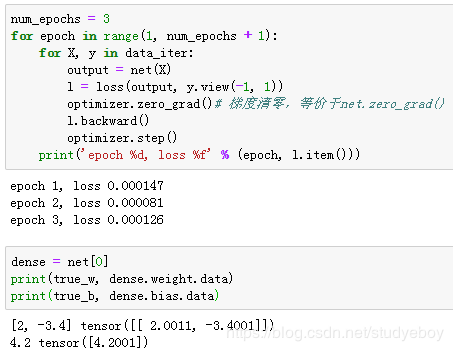
小结
- 使用Gluon可以更简洁的实现模型。
- 在Gluon中,data模块提供了有关数据处理的工具,nn模块定义了大量神经网络的层,loss模块定义了各种损失函数。
- MXNet的init模块提供了模型参数初始化的各种方法。
softmax回归
分类问题
softmax回归模型
softmax计算
单样本分类的矢量计算表达式
小批量样本分类的矢量计算表达式
交叉熵损失函数
证明
模型预测及评价(线性回归没有评价)
小结
- softmax回归适用于分类问题。它使用softmax运算输出类别的概率分布。
- softmax回归是一个单层神经网络,输出个数等于分类问题中的类别个数。
- 交叉熵适合衡量两个概率分布的差异。
图像分类数据集(Fashion-MNIST)
获取数据集
- MXNet
导入需要的包或模块。

通过Gluon的data包来下载这个数据集。第一次调用时会自动从网上获取数据。通过参数trian来指定获取训练数据集或测试数据集(testing data set)。测试数据集也叫测试集(testing set),只用来评价模型的表现,并不用来训练模型。
训练集中和测试集中的每个类别的图像分别为6000和1000。因为有10个类别,所以训练集和测试集的样本数分别为60000和10000。

用方括号[]来访问任意一个样本,获取第一个样本的图像和标签。

变量feature对应高和宽均为28像素的图像。每个像素的数值为0到255之间的8位无符号整数(uint8)。它使用三维的NDArray存储。其中的最后一维是通道数。因为数据集中是灰度图像,所以通道数为1。为了表达简洁,将高和宽分别为h和w像素的图像的形状记为hxw或(h,w)。

图像的标签使用NumPy的标量表示。它的类型为32为整数(int32)。

Fashion-MNIST中一共包括了10个类别,分别为t-shirt(T恤)、trouser(裤子)、pullover(套衫)、dress(连衣裙)、coat(外套)、sandal(凉鞋)、shirt(衬衫)、sneaker(运动鞋)、bag(包)和ankle boot(短靴)。用函数可以将数值标签转成相应的文本标签。

定义一个可以在一行里画出多张图像和对应标签的函数。

迅雷书记集中前9个样本的图像和文本标签。

- PyTorch





读取小批量
小结
- Fashion-MNIST是一个10类服饰分类数据集。
- 高和宽分别为 h 和 w 像素的图像的形状记为 h×w 或(h,w)。
softmax回归的从零开始实现
获取和读取数据
初始化模型参数
- MXNet
使用向量表示每个样本。已知每个样本输入是高和宽均为28像素的图像。模型的输入向量的长度为28x28=784,该向量的每个元素对应图像中每个像素。由于图像有10个类别,单层神经网络输出层的输出个数为10,因此softmax回归的权重和偏差参数分别为784x10和1x10的矩阵。

为模型参数附上梯度。

- PyTorch


实现softmax运算
对多维NDArray按维度操作。给定一个NDArray矩阵X。可以只对其中同一列(axis=0)或同一行(axis=1)的元素求和,并在结果中保留行和列这两个维度(keepdims=True)。


softmax运算。在下面的函数中,矩阵X的行数是样本数,列数是输出个数。为了表达样本预测各个输出的概率,softmax运算会先通过exp函数对每个元素做指数运算,再对exp矩阵同行元素求和,最后令矩阵每行格元素与该元素之和相除。这样一来,最终得到的矩阵每行元素和为1且非负。因此,该矩阵每行都是合法的概率分布。softmax运算的输出矩阵中的任意一行元素代表了一个样本在各个输出类别上的预测概率。


通过下面的例子可以看到,对于随机输入,定义的softmax函数将每个元素变成了非负数,且每一行和为1.
![]()

定义模型
有了softmax运算,可以定义softmax回归模型了。通过reshape函数将每张图像改成长度为num_inputs的向量。
![]()
![]()
定义损失函数
为了得到标签的预测概率,可以使用pick函数。在下面的例子中,变量y_hat是2个样本在3个类别的预测概率,变量y是这2个样本的标签类别。通过使用pick函数,可以得到这2个样本的标签的预测概率。标签类别的离散值是从0开始逐一递增的。
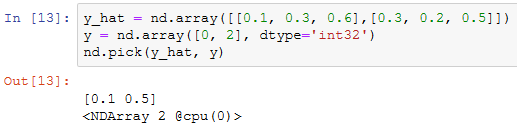

交叉熵损失函数。


计算分类准确率
给定一个类别的预测概率分布y_hat,把预测概率最大的类别作为输出类别。如果它与真实类别y一致,说明这次预测是正确的。分类准确率即正确预测数量与总预测数量比值。
为了演示准确率的计算,定义准确率accuray函数。其中y_hat.argmax(axis=1)返回矩阵y_hat每行中最大元素的索引,且返回结果与变量y形状相同。相等条件判断式(y_hat.argmax(axis=1)==y)是一个值为0(相等为假)或1(相等为真)的NDArray。由于标签类别类型为整数,需要先将变量y变换为浮点数再进行相等条件判断。
![]()

继续使用在演示pick函数时定义的变量y_hat和y,并将它们分别作为预测概率分布和标签。可以看到,第一个样本预测类别为2(该行最大元素0.6在本行的索引为2),与真实标签0不一致;第二个样本预测类别为2(该行最大元素0.5在本行的索引为2),与真实标签2一致。因此,这两个样本上的分类准去率为0.5。


类似的,评价模型net在数据集data_iter上的准确率。


因为我们随机初始化了模型net,所以这个随机模型的准确率应该接近于类别个数10的倒数0.1。

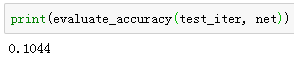
训练模型
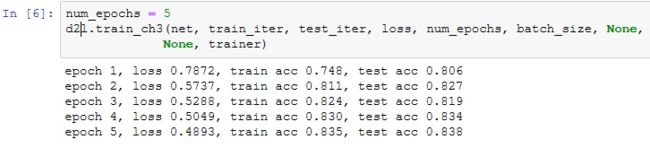
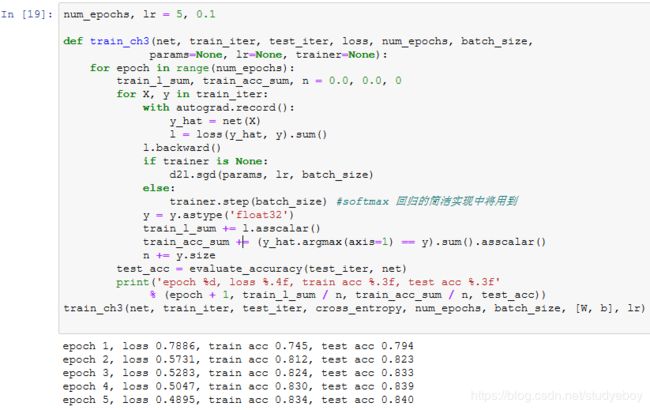
使用小批量随机梯度下降来优化模型的损失函数。在训练模型时,迭代周期数num_epochs和学习率lr都是可以调的超参数。改变它们的值可能会得到分类更准确的模型。
![]()
预测
训练完成 后,可以对图像进行分类了。给定一系列图像(第三行图像输出),比较它们的真实标签(第一行文本输出)和模型预测结果(第二行文本输出)。


小结
使用softmax回归做多类别分类。与训练线性回归相比,步骤都非常相似,获取数据并读取数据、定义模型和损失函数并使用优化算法训练模型。事实上,绝大多数深度学习模型的训练都有着类似的步骤。
softmax回归的简洁实现
使用Gluon来实现一个softmax回归模型。首先导入所需的包或模块。


获取和读取数据
我们仍然使用Fashion-MNIST数据集和上一节中设置的批量大小。
![]()

定义和初始化模型
softmax回归的输出层是一个全连接层。因此,我们添加一个输出个数为10的全连接层。我们使用均值为0、标准差为0.01的正态分布随机初始化模型的权重参数。



softmax和交叉熵损失函数
分开定义softmax运算和交叉熵损失函数可能会造成数值不稳定。因此,Gluon提供了一个包括softmax运算和交叉熵损失计算的函数。它的数值稳定性更好。
![]()
![]()
定义优化算法
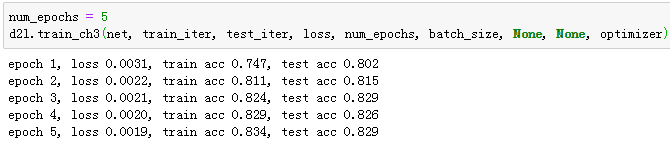
训练模型
小结
- Gluon提供的函数往往具有更好的数值稳定性。
- 可以使用Gluon更简洁的实现softmax回归。
多层感知机
隐藏层
激活函数
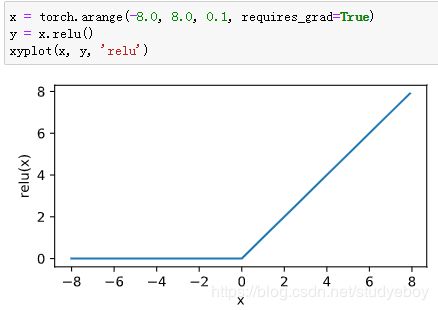
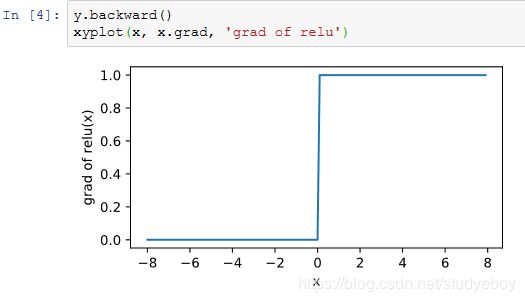
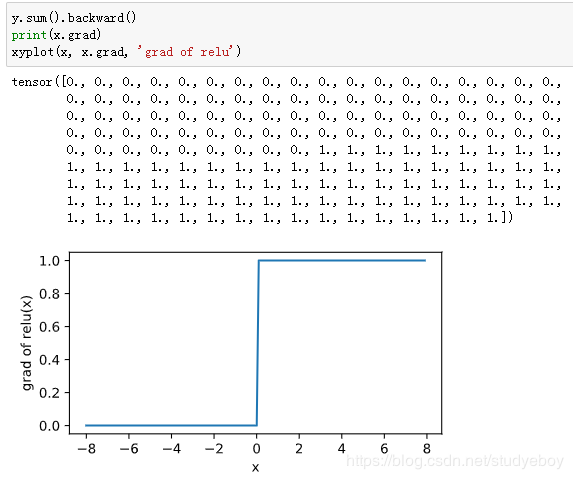
ReLU函数
sigmoid函数
tanh函数
多层感知机
小结
- 多层感知机在输出层与输入层之间加入了一个或多个全连接隐藏层,并通过激活函数对隐藏层输出进行变换。
- 常用的激活函数包括ReLU函数、sigmoid函数和tanh函数。
多层感知机的从零开始实现
获取和读取数据
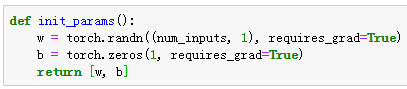
定义模型参数
定义激活函数
定义模型
定义损失函数
训练模型
多层感知机的简洁实现
定义模型
读取数据并训练模型
![]()
![]()
模型选择、欠拟合和过拟合
训练误差和泛化误差
![]()
模型选择
验证数据集
K折交叉验证
![]()
欠拟合和过拟合
模型复杂度
模型复杂度由参数增加(不同阶数项的系数)而增加,深度学习模型不一定要通过表达阶数来拟合数据,有足够的参数就可以了。
深度学习模型的复杂度某种意义上就等同于参数的数量。
训练数据集大小
多项式函数拟合实验
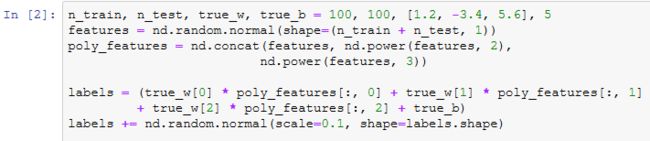
生成数据集
定义、训练和测试模型
定义作图函数semilogy,其中y轴使用了对数尺度。
![]()

和线性回归一样,多项式函数拟合也使用平方损失函数。因为要尝试使用不同复杂度的模型来拟合生成的数据集,所以包模型定义部分放在fit_and_plot函数中。

![]()
三阶多项式函数拟合(正常)
使用与数据生成函数同阶的三阶多项式函数拟合。实验表明,这个模型的训练误差和测试集数据集的误差都较低。训练出的模型参数也接近真实值: w 1 = 1.2 , w 2 = − 3.4 , w 3 = 5.6 , b = 5 w_1=1.2, w_2=-3.4,w_3=5.6,b=5 w1=1.2,w2=−3.4,w3=5.6,b=5

![]()
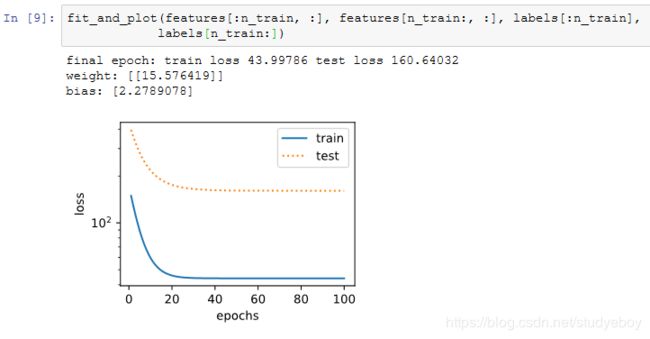
线性函数拟合(欠拟合)
线性函数拟合,很明显,该模型的训练误差在迭代早期下降后便很难继续降低。在完成最后一次迭代周期后,训练误差依旧很高。线性模型在非线性模型(如三阶多项式函数)生成的数据集上容易欠拟合。

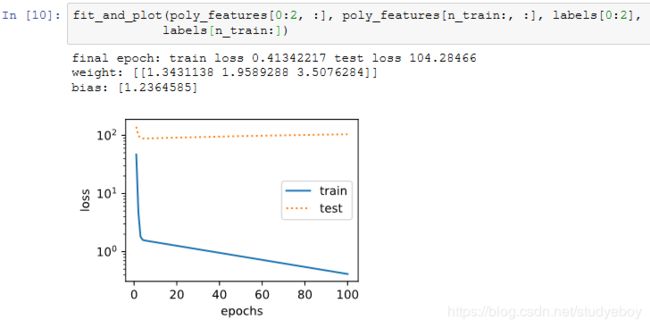
训练样本不足(过拟合)
事实上,即便使用与数据生成模型同阶的三阶多项式函数模型,如果训练样本不足,该模型依然容易过拟合。如果只使用两个样本来训练模型。显然,训练样本过少了,甚至少于模型参数的数量。这使模型显得过于复杂,以至于容易被训练数据中的噪声影响。在迭代过程中,尽管训练误差较低,但是测试数据集上的误差却很高。这就是典型的过拟合现象。
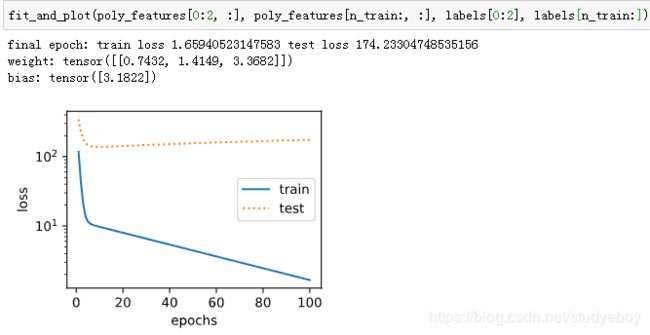
小结
- 由于无法从训练误差估计泛化误差,一味地降低训练误差并不意味着泛化误差一定会降低。机器学习模型应关注降低泛化误差。
- 可以使用验证数据集来进行模型选择。
- 欠拟合值模型无法得到较低的训练误差,过拟合指模型的训练误差远小于它在测试集上的误差。
- 应选择复杂度合适的模型并避免使用过少的训练样本。
权重衰减
模型的训练误差远小于它在测试集上的误差,虽然增大训练数据集可能会减轻过拟合,但是获取额外的训练数据往往代价高昂。可以使用权重衰减(weight decay)方法应对过拟合。
方法
高维线性回归实验
从零开始实现
从零开始实现权重衰减的方法。通过在目标函数后添加L2范数惩罚项来实现权重衰减。
初始化模型参数
定义L2范数惩罚项
定义训练和测试
定义在训练数据集和测试数据集上分别训练和测试模型。在计算最终的损失函数时添加了L2范数惩罚项。


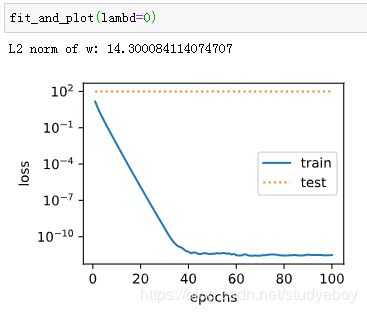
观察过拟合
训练并测试高维线性回归模型。当lambda设为0时,没有使用权重衰减。结果训练误差远小于测试集上的误差。这是典型的过拟合现象。

使用权重衰减
通过使用权重衰减,训练误差虽然有所提高,但测试集上的误差有所下降。过拟合现象得到一定程度的缓解。另外,权重参数的L2范数比不使用权重衰减时的更小,此时的权重参数更接近0。


简洁实现
直接在构造Trainer实例时通过wd参数来指定权重衰减超参数。默认下,Gluon会对权重和偏差同时衰减。可以分别对权重和偏差构造Trainer实例,从而只对权重衰减。
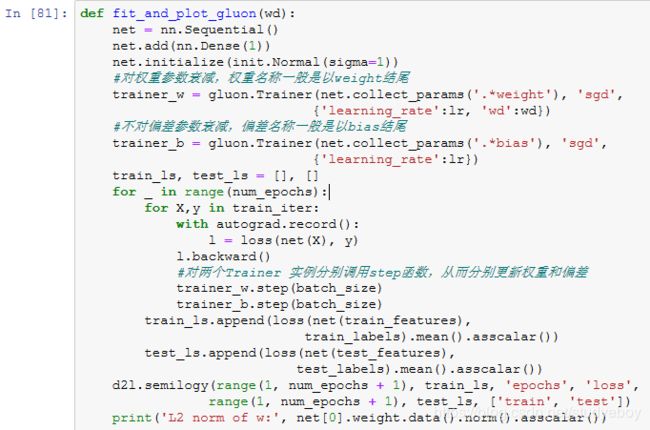

与从零开始实现权重衰减的实验现象类似,使用权重衰减可以在一定程度上缓解过拟合问题。

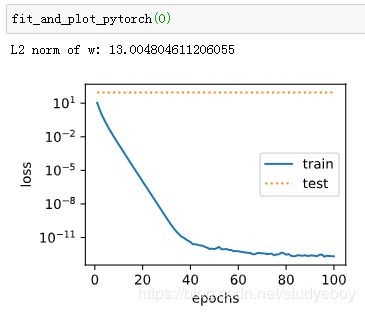


小结
- 正则化通过为模型损失函数添加惩罚项使学出的模型参数值较小,是应对过拟合的常用手段。
- 权重衰减等价于L2范数正则化,通常会使学到的权重参数的元素较接近0。
- 权重衰减可以通过Gluon的wd超参数来指定。
- 可以定义多个Trainer实例对不同的模型参数使用不同的迭代方法。
丢弃法
除了权重衰减以外,深度学习模型常常使用丢弃法(dropout)来应对过拟合问题。丢弃法有一些不同的变体。本节中提到的丢弃法特指倒置丢弃法(inverted dropout)。
方法
从零开始实现
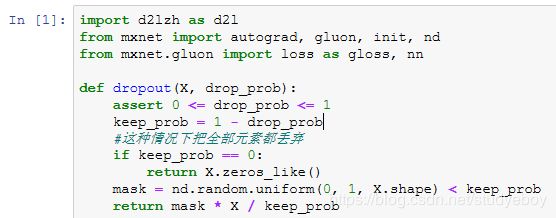
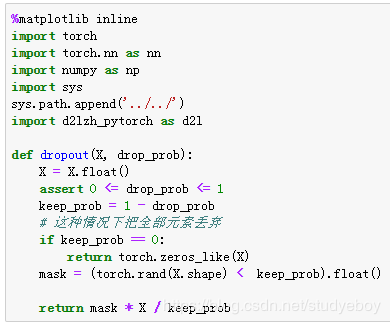
根据丢弃法的定义,可以很容易的实现它。下面的dropout函数将以drop_prob的概率丢弃NDArray输入X中的元素。
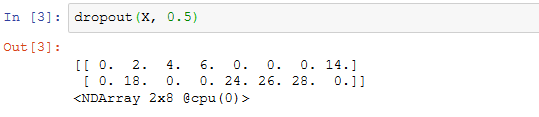
例子测试dropout函数,其中丢弃概率分别为0,0.5,和1。
![]()




定义模型参数
使用Fashion-MNIST数据集,定义一个包含两个隐藏层得的多层感知机,其中两个隐藏层的输出个数都是256。

![]()
定义模型
定义的模型将全连接和激活函数ReLU串起来,并对每个激活函数的输出使用丢弃法。分别设置各个层的丢弃概率。通常的建议是把靠近输入层的丢弃概率设置的小一点。所以第一个隐藏层的丢弃概率设置为0.2,第二个隐藏层的丢弃概率设置为0.5。根据is_training函数来判断运行模式Wie训练还是测试,并只需在训练模式下使用丢弃法。


训练和测试模型
简洁实现
在Gluon中,只需要在全连接层后添加Dropout层并指定丢弃概率。在训练模型时,Dropout层将以指定的丢弃概率随机丢弃上一层的输出元素;在测试模型时,Dropout层并不发挥作用。
![]()
![]()
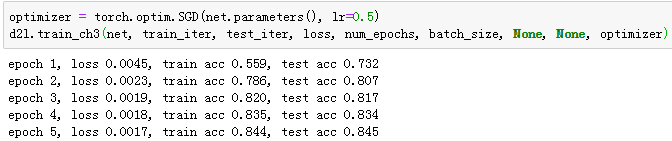
训练并测试模型。
![]()
小结
- 可以通过使用丢弃法应对过拟合。
- 丢弃法只在训练模型时使用。
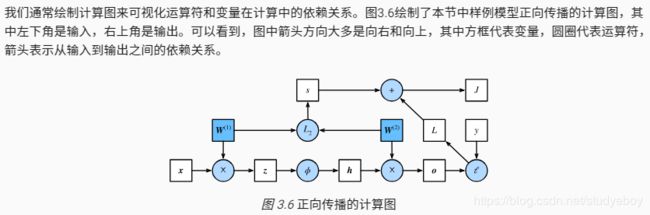
正向传播、反向传播和计算图
![]()
正向传播
正向传播的计算图
反向传播
训练深度学习模型
小结
- 正向传播沿着从输入层到输出层的顺序,依次计算并存储神经网络中间变量。
- 反向传播沿着从输出层到输入层的顺序,依次计算并存储神经网络中间变量和参数的梯度。
- 在训练深度学习模型时,正向传播和反向传播相互依赖。
数值稳定性和模型初始化
理解了正向传播与反向传播以后,我们来讨论一下深度学习模型的数值稳定性问题以及模型参数的初始化方法。深度模型有关数值稳定性的典型问题是衰减(vanishing)和爆炸(explosion)。
衰减和爆炸
随机初始化模型参数
MXNet的默认随机初始化
![]()
Xavier随机初始化
小结
- 深度模型有关数值稳定性的典型问题是衰减和爆炸。当神经网络的层数较多时,模型的数值稳定性容易变差。
- 通常需要随机初始化神经网络的模型参数,如权重参数。
实战Kaggle比赛:房价预测
Kaggle比赛
获取和读取数据
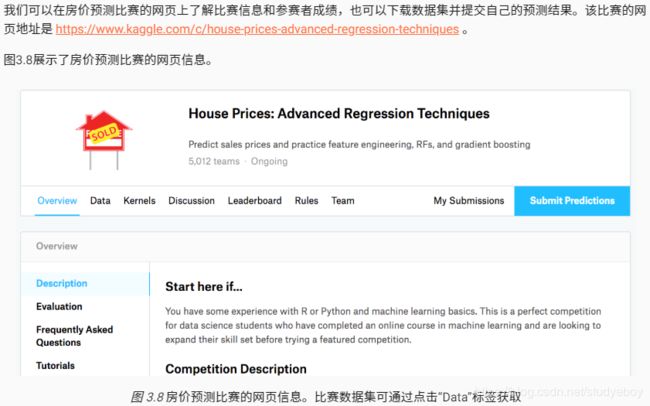
比赛数据分为训练数据集和测试数据集。两个数据集都包括每栋房子的特征,如街道类型、建造年份、房顶类型、地下室状况等特征值。这些特征值有连续的数字、离散的标签甚至是缺失值“na”。只有训练数据集包括了每栋房子的价格,也就是标签。我们可以访问比赛网页,点击图3.8中的“Data”标签,并下载这些数据集。
我们将通过pandas库读入并处理数据。在导入本节需要的包前请确保已安装pandas库,否则请参考下面的代码注释。

解压后的数据位于…/data目录,它包括两个csv文件。下面使用pandas读取这两个文件。
![]()
![]()
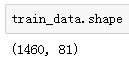
训练数据集包括1460个样本、80个特征和1个标签。

测试数据集包括1459个样本和80个特征。我们需要将测试数据集中每个样本的标签预测出来。

![]()
让我们来查看前4个样本的前4个特征(对应索引为:0:4)、后2个特征(对应索引为:-3, -2)和标签(SalePrice)(对应索引为:-1):
![]()

可以看到第一个特征是Id,它能帮助模型记住每个训练样本,但难以推广到测试样本,所以我们不使用它来训练。我们将所有的训练数据和测试数据的79个特征按样本连结。
![]()
![]()
预处理数据
我们对连续数值的特征做标准化(standardization):设该特征在整个数据集上的均值为 μ ,标准差为 σ 。那么,我们可以将该特征的每个值先减去 μ 再除以 σ 得到标准化后的每个特征值。对于缺失的特征值,我们将其替换成该特征的均值。


接下来将离散数值转成指示特征。举个例子,假设特征MSZoning里面有两个不同的离散值RL和RM,那么这一步转换将去掉MSZoning特征,并新加两个特征MSZoning_RL和MSZoning_RM,其值为0或1。如果一个样本原来在MSZoning里的值为RL,那么有MSZoning_RL=1且MSZoning_RM=0。


可以看到这一步转换将特征数从79增加到了331。
最后,通过values属性得到NumPy格式的数据,并转成NDArray方便后面的训练。


训练模型
我们使用一个基本的线性回归模型和平方损失函数来训练模型。

![]()



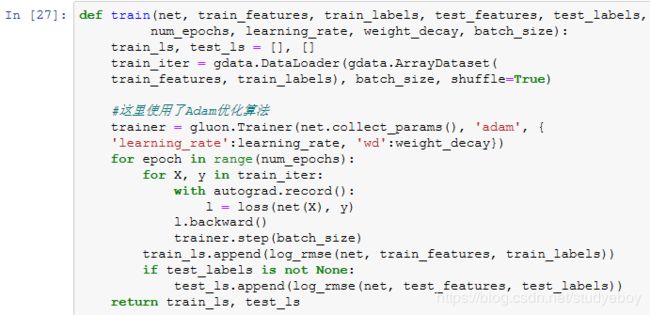
下面的训练函数跟本章中前几节的不同在于使用了Adam优化算法。相对之前使用的小批量随机梯度下降,它对学习率相对不那么敏感。

K折交叉验证
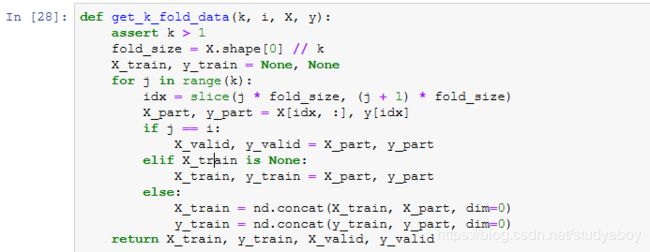
K 折交叉验证将被用来选择模型设计并调节超参数。下面实现了一个函数,它返回第i折交叉验证时所需要的训练和验证数据。

在 K 折交叉验证中我们训练 K 次并返回训练和验证的平均误差。
![]()

模型选择
我们使用一组未经调优的超参数并计算交叉验证误差。可以改动这些超参数来尽可能减小平均测试误差。
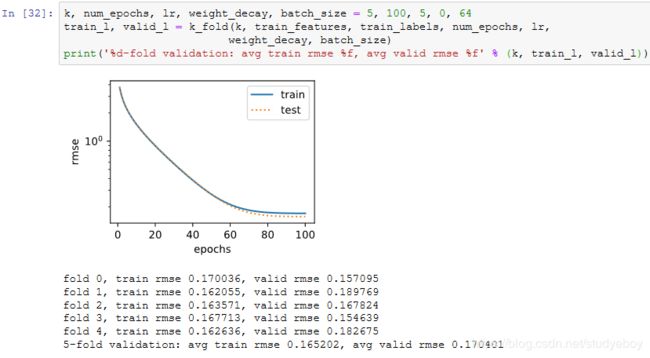
![]()
有时候你会发现一组参数的训练误差可以达到很低,但是在 K 折交叉验证上的误差可能反而较高。这种现象很可能是由过拟合造成的。因此,当训练误差降低时,我们要观察 K 折交叉验证上的误差是否也相应降低。
预测并在Kaggle提交结果
下面定义预测函数。在预测之前,我们会使用完整的训练数据集来重新训练模型,并将预测结果存成提交所需要的格式。


设计好模型并调好超参数之后,下一步就是对测试数据集上的房屋样本做价格预测。如果我们得到与交叉验证时差不多的训练误差,那么这个结果很可能是理想的,可以在Kaggle上提交结果。



小结
- 通常需要对真实数据做预处理。
- 可以使用K折交叉验证来选择模型并调节超参数。
深度学习计算
模型构造
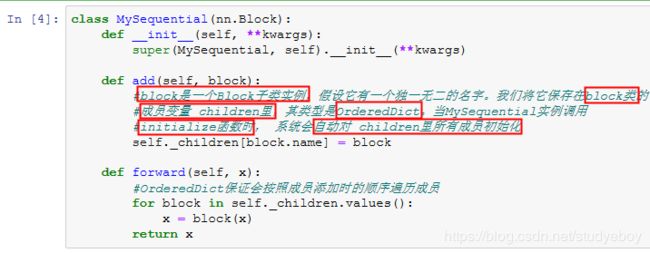
基于Block类的模型构造方法:它让模型构造更加灵活。
继承Block类来构造模型
Sequential类继承自Block类


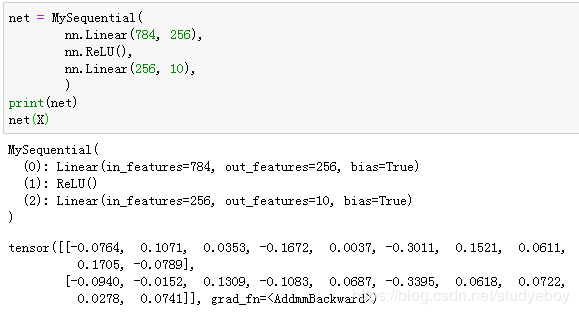
我们用MySequential类来实现前面描述的MLP类,并使用随机初始化的模型做一次前向计算。
![]()
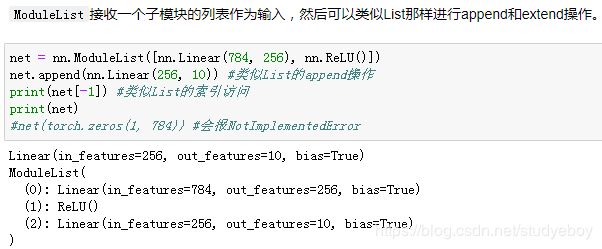

![]()
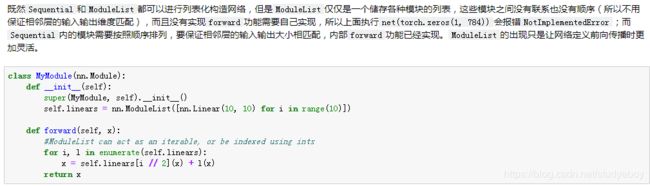
构造复杂的模型



在这个FancyMLP模型中,我们使用了常数权重rand_weight(注意它不是模型参数)、做了矩阵乘法操作(nd.dot)并重复使用了相同的Dense层。下面我们来测试该模型的随机初始化和前向计算。
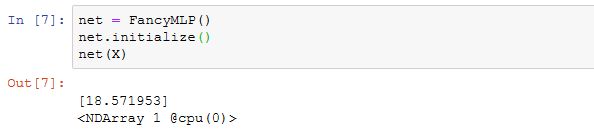

因为FancyMLP和Sequential类都是Block类的子类,所以我们可以嵌套调用它们。


小结
- 可以通过继承Block类来构造模型。
- Sequential类继承自Block类。
- 虽然Sequential类可以使模型构造更加简单,但直接继承Block类可以极大的拓展模型构造的灵活性。
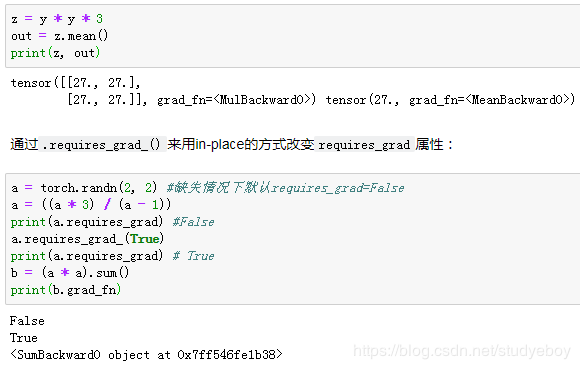
模型参数的访问、初始化和共享
访问模型参数


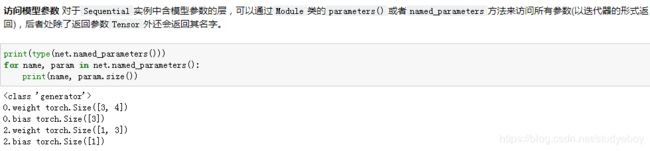


![]()

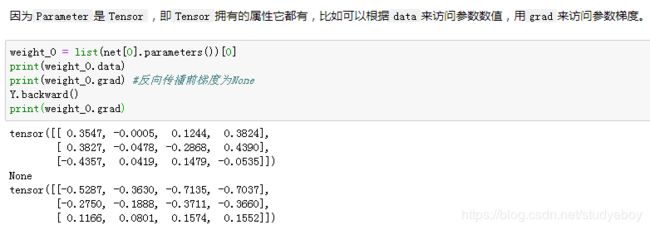
Gluon里参数类型为Parameter类,它包含参数和梯度的数值,可以分别通过data函数和grad函数来访问。因为我们随机初始化了权重,所以权重参数是一个由随机数组成的形状为(256, 20)的NDArray。
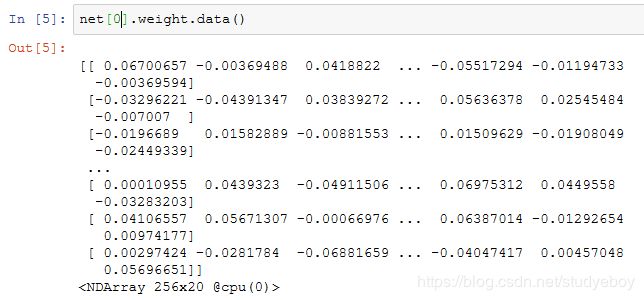
权重梯度的形状和权重的形状一样。因为我们还没有进行反向传播计算,所以梯度的值全为0。
类似地,我们可以访问其他层的参数,如输出层的偏差值。
最后,我们可以使用collect_params函数来获取net变量所有嵌套(例如通过add函数嵌套)的层所包含的所有参数。它返回的同样是一个由参数名称到参数实例的字典。
![]()
这个函数可以通过正则表达式来匹配参数名,从而筛选需要的参数。

初始化模型参数
模型的默认初始化方法:权重参数元素为[-0.07, 0.07]之间均匀分布的随机数,偏差参数则全为0。但我们经常需要使用其他方法来初始化权重。MXNet的init模块里提供了多种预设的初始化方法。在下面的例子中,我们将权重参数初始化成均值为0、标准差为0.01的正态分布随机数,并依然将偏差参数清零。
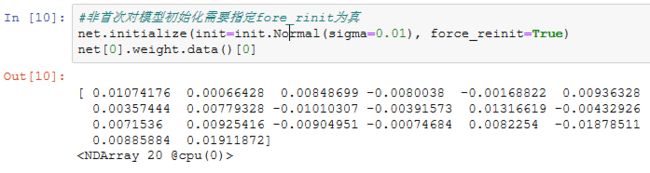
下面使用常数来初始化权重参数。

如果只想对某个特定参数进行初始化,我们可以调用Parameter类的initialize函数,它与Block类提供的initialize函数的使用方法一致。下例中我们对隐藏层的权重使用Xavier随机初始化方法。

![]()
自定义初始化方法

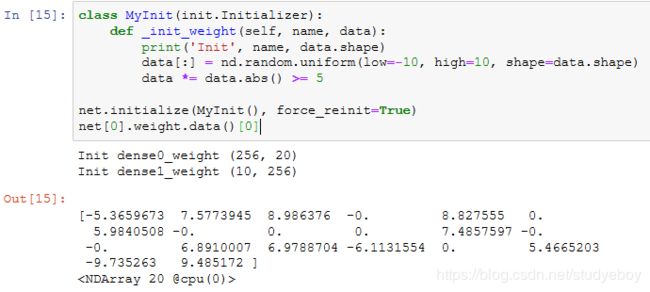
此外,我们还可以通过Parameter类的set_data函数来直接改写模型参数。例如,在下例中我们将隐藏层参数在现有的基础上加1。

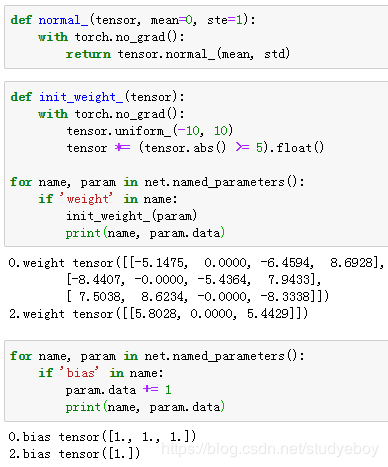
共享模型参数


我们在构造第三隐藏层时通过params来指定它使用第二隐藏层的参数。因为模型参数里包含了梯度,所以在反向传播计算时,第二隐藏层和第三隐藏层的梯度都会被累加在shared.params.grad()里。
小结
- 有多种方法来访问、初始化和共享模型参数。
- 可以自定义初始化方法。
模型参数的延后初始化
延后初始化


注意,虽然MyInit被调用时会打印模型参数的相关信息,但上面的initialize函数执行完并未打印任何信息。由此可见,调用initialize函数时并没有真正初始化参数。下面我们定义输入并执行一次前向计算。

这时候,有关模型参数的信息被打印出来。在根据输入X做前向计算时,系统能够根据输入的形状自动推断出所有层的权重参数的形状。系统在创建这些参数之后,调用MyInit实例对它们进行初始化,然后才进行前向计算。
当然,这个初始化只会在第一次前向计算时被调用。之后我们再运行前向计算net(X)时则不会重新初始化,因此不会再次产生MyInit实例的输出。
![]()

避免延后初始化
小结
- 系统将真正的参数初始化延后到获得足够信息时才执行的行为叫作延后初始化。
- 延后初始化的主要好处是让模型构造更加简单。例如,我们无需人工推测每个层的输入个数。
- 也可以避免延后初始化。
自定义层
![]()
不含模型参数的自定义层



我们可以实例化这个层,然后做前向计算。
![]()

我们也可以用它来构造更复杂的模型。

![]()
下面打印自定义层各个输出的均值。因为均值是浮点数,所以它的值是一个很接近0的数。


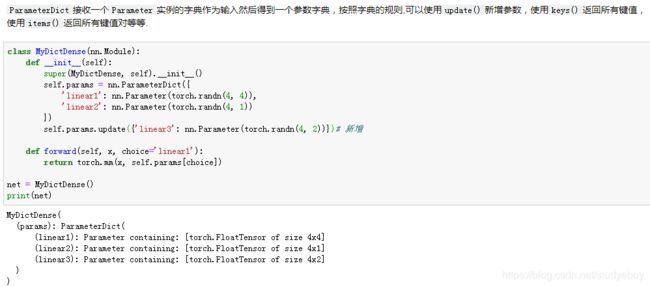
含模型参数的自定义层


现在我们尝试实现一个含权重参数和偏差参数的全连接层。它使用ReLU函数作为激活函数。其中in_units和units分别代表输入个数和输出个数。

下面,我们实例化MyDense类并访问它的模型参数。

我们可以直接使用自定义层做前向计算。

我们也可以使用自定义层构造模型。它和Gluon的其他层在使用上很类似。
![]()

![]()
小结
- 可以通过Block类自定义神经网络中的层,从而可以被重复调用。
读取和存储
到目前为止,我们介绍了如何处理数据以及如何构建、训练和测试深度学习模型。然而在实际中,我们有时需要把训练好的模型部署到很多不同的设备。在这种情况下,我们可以把内存中训练好的模型参数存储在硬盘上供后续读取使用。
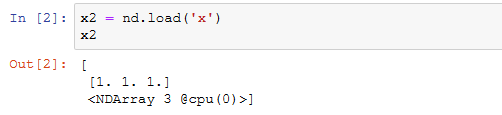
读写NDArray
我们可以直接使用save函数和load函数分别存储和读取NDArray。下面的例子创建了NDArray变量x,并将其存在文件名同为x的文件里。


然后我们将数据从存储的文件读回内存。

我们还可以存储一列NDArray并读回内存。
![]()

我们甚至可以存储并读取一个从字符串映射到NDArray的字典。
![]()

读写Gluon模型的参数
除NDArray以外,我们还可以读写Gluon模型的参数。Gluon的Block类提供了save_parameters函数和load_parameters函数来读写模型参数。为了演示方便,我们先创建一个多层感知机,并将其初始化。回忆“模型参数的延后初始化”一节,由于延后初始化,我们需要先运行一次前向计算才能实际初始化模型参数。
![]()
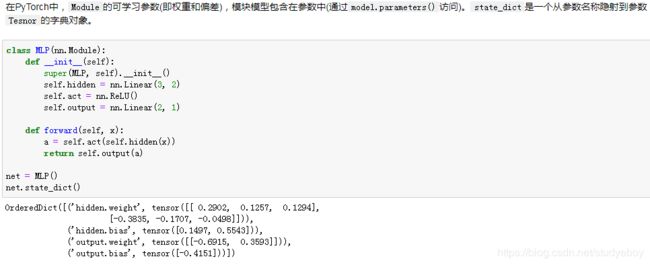

下面把该模型的参数存成文件,文件名为mlp.params。
![]()
接下来,我们再实例化一次定义好的多层感知机。与随机初始化模型参数不同,我们在这里直接读取保存在文件里的参数。

因为这两个实例都有同样的模型参数,那么对同一个输入X的计算结果将会是一样的。我们来验证一下。


小结
- 通过save和load函数可以很方便的读写NDArray。
- 通过load_parameters函数和load_parameters函数可以很方便的读写Gluon模型的参数。
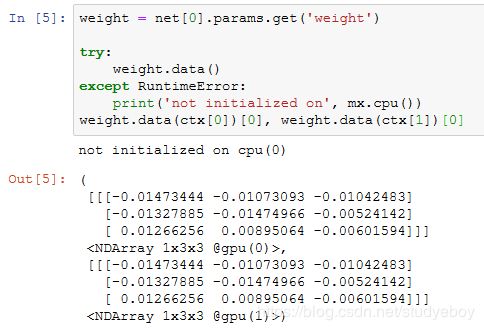
GPU计算
计算设备
NDArray的GPU计算
在默认情况下,NDArray存在内存上。因此,之前我们每次打印NDArray的时候都会看到@cpu(0)这个标识。
![]()
我们可以通过NDArray的context属性来查看该NDArray所在的设备。

GPU 上的存储


假设至少有2块GPU,下面代码将会在gpu(1)上创建随机数组。
![]()
除了在创建时指定,我们也可以通过copyto函数和as_in_context函数在设备之间传输数据。下面我们将内存上的NDArray变量x复制到gpu(0)上。
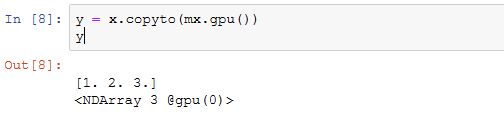

需要区分的是,如果源变量和目标变量的context一致,as_in_context函数使目标变量和源变量共享源变量的内存或显存。

而copyto函数总是为目标变量开新的内存或显存。

GPU上的计算
MXNet的计算会在数据的context属性所指定的设备上执行。为了使用GPU计算,我们只需要事先将数据存储在显存上。计算结果会自动保存在同一块显卡的显存上。
![]()

Tensor的GPU计算(PyTorch)
Gluon的GPU计算
同NDArray类似,Gluon的模型可以在初始化时通过ctx参数指定设备。下面的代码将模型参数初始化在显存上。

当输入是显存上的NDArray时,Gluon会在同一块显卡的显存上计算结果。
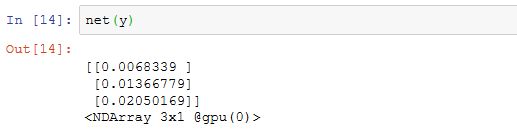
下面我们确认一下模型参数存储在同一块显卡的显存上。

模型的GPU计算(PyTorch)
![]()
小结
- MXNet可以指定用来存储和计算的设备,如使用内存的CPU或者使用显存的GPU。在默认情况下,MXNet会将数据创建在内存,然后利用CPU来计算。
- MXNet要求计算的所有输入数据都在内存或同一块显卡的显存上。
卷积神经网络
二维卷积层
![]()
二维互相关运算
二维卷积层



卷积窗口形状为 p×q 的卷积层称为 p×q 卷积层。同样, p×q 卷积或 p×q 卷积核说明卷积核的高和宽分别为 p 和 q 。
图像中物体边缘检测
一个卷积层的简单应用:检测图像中物体的边缘,即找到像素变化的位置。首先我们构造一张 6×8 的图像(即高和宽分别为6像素和8像素的图像)。它中间4列为黑(0),其余为白(1)。


构造一个高和宽分别为1和2的卷积核K。当它与输入做互相关运算时,如果横向相邻元素相同,输出为0;否则输出为非0。
![]()
![]()
将输入X和我们设计的卷积核K做互相关运算。可以看出,我们将从白到黑的边缘和从黑到白的边缘分别检测成了1和-1。其余部分的输出全是0。


由此,我们可以看出,卷积层可通过重复使用卷积核有效地表征局部空间。
通过数据学习核数组



可以看到,10次迭代后误差已经降到了一个比较小的值。现在来看一下学习到的核数组。


可以看到,学到的核数组与我们之前定义的核数组K较接近。
互相关运算和卷积运算
特征图和感受野
小结
- 二维卷积层的核心计算是二维互相关运算。在最简单的形式下,它对二维输入数据和卷积核做互相关运算然后加上偏差。
- 可以设计卷积核来检测图像中的边缘。
- 可以通过数据来学习卷积核
填充和步幅
填充

创建一个高和宽为3的二维卷积层,然后设输入高和宽两侧的填充数分别为1。给定一个高和宽为8的输入,我们发现输出的高和宽也是8。

![]()
当卷积核的高和宽不同时,我们也可以通过设置高和宽上不同的填充数使输出和输入具有相同的高和宽。


步幅


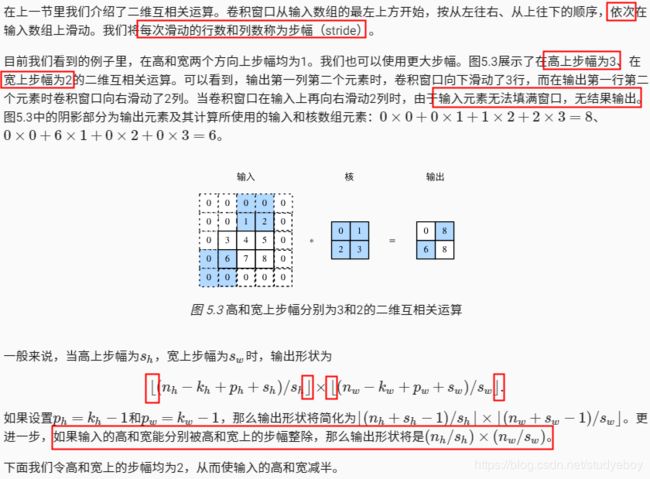
接下来是一个稍微复杂点儿的例子。


为了表述简洁,当输入的高和宽两侧的填充数分别为 ph 和 pw 时,我们称填充为 (ph,pw) 。特别地,当 ph=pw=p 时,填充为 p 。当在高和宽上的步幅分别为 sh 和 sw 时,我们称步幅为 (sh,sw) 。特别地,当 sh=sw=s 时,步幅为 s 。在默认情况下,填充为0,步幅为1。
小结
- 填充可以增加输出的高和宽。这常用来使输出与输入具有相同的高和宽。
- 步幅可以减小输出的高和宽,例如输出的高和宽仅为输入的高和宽的1/n(n为大于1的整数)。
多输入通道和多输出通道
多输入通道
多输出通道



![]()
我们将核数组K同K+1(K中每个元素加一)和K+2连结在一起来构造一个输出通道数为3的卷积核。

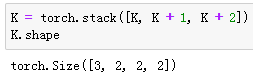
下面我们对输入数组X与核数组K做互相关运算。此时的输出含有3个通道。其中第一个通道的结果与之前输入数组X与多输入通道、单输出通道核的计算结果一致。


1x1卷积层



经验证,做1×1卷积时,以上函数与之前实现的互相关运算函数corr2d_multi_in_out等价。


在之后的模型里我们将会看到1×1卷积层被当作保持高和宽维度形状不变的全连接层使用。于是,我们可以通过调整网络层之间的通道数来控制模型复杂度。
小结
- 使用多通道可以拓展卷积层的模型参数。
- 假设将通道维当作特征维,将高和宽维度上的元素当成数据样本,那么1x1卷积层的作用与全连接层等价。
- 1x1卷积层通常用来调整网络层之间的通道数,并控制模型复杂度。
池化层
二维最大池化层和平均池化层

下面把池化层的前向计算实现在pool2d函数里。它跟二维卷积层的corr2d函数非常类似,唯一的区别在计算输出Y上。


输入数组X来验证二维最大池化层的输出。


实验一下平均池化层。
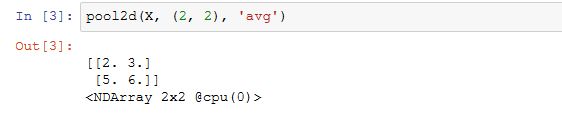

填充和步幅
![]()

默认情况下,MaxPool2D实例里步幅和池化窗口形状相同。下面使用形状为(3, 3)的池化窗口,默认获得形状为(3, 3)的步幅。
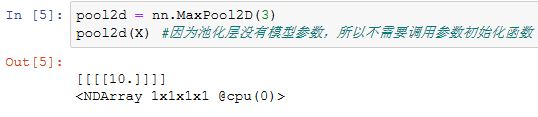
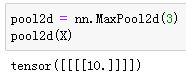
可以手动指定步幅和填充。
![]()
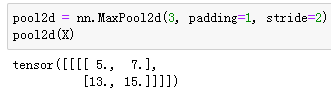
也可以指定非正方形的池化窗口,并分别指定高和宽上的填充和步幅。
![]()

多通道
小结
- 最大池化和平均池化分别取池化窗口中输入元素的最大值和平均值作为输出。
- 池化层的一个主要作用是缓解卷积层对位置的过度敏感性。
- 可以指定池化层的填充和步幅。
- 池化层的输出通道数跟输入通道数相同。
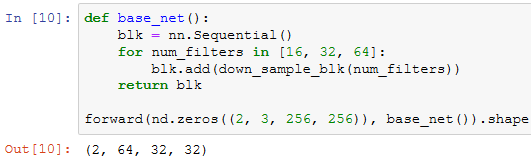
卷积神经网络(LeNet)
![]()
LeNet模型



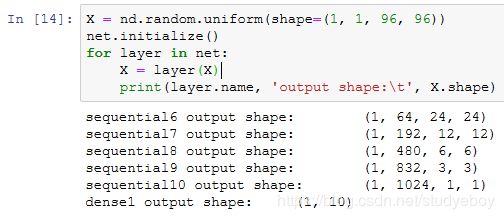
构造一个高和宽均为28的单通道数据样本,并逐层进行前向计算来查看每个层的输出形状。

可以看到,在卷积层块中输入的高和宽在逐层减小。卷积层由于使用高和宽均为5的卷积核,从而将高和宽分别减小4,而池化层则将高和宽减半,但通道数则从1增加到16。全连接层则逐层减少输出个数,直到变成图像的类别数10。
获取数据和训练模型
下面我们来实验LeNet模型。实验中,我们仍然使用Fashion-MNIST作为训练数据集。


因为卷积神经网络计算比多层感知机要复杂,建议使用GPU来加速计算。我们尝试在gpu(0)上创建NDArray,如果成功则使用gpu(0),否则仍然使用CPU。

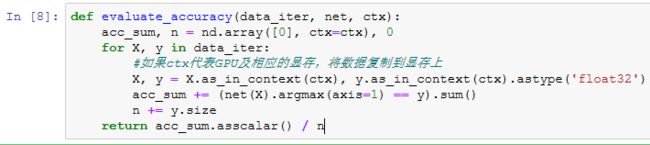
相应地,我们对“softmax回归的从零开始实现”一节中描述的evaluate_accuracy函数略作修改。由于数据刚开始存在CPU使用的内存上,当ctx变量代表GPU及相应的显存时,我们通过“GPU计算”一节中介绍的as_in_context函数将数据复制到显存上,例如gpu(0)。
![]()
我们同样对“softmax回归的从零开始实现”一节中定义的train_ch3函数略作修改,确保计算使用的数据和模型同在内存或显存上。


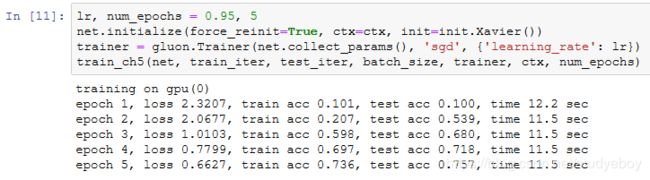
我们重新将模型参数初始化到设备变量ctx之上,并使用Xavier随机初始化。损失函数和训练算法则依然使用交叉熵损失函数和小批量随机梯度下降。
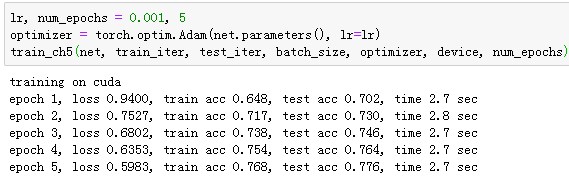
小结
- 卷积神经网络ius含卷积层的网络。
- LeNet交替使用卷积层和最大池化层后接全连接层来进行图像分类。
深度卷积神经网络(AlexNet)
![]()
学习特征表示
缺失要素一:数据
缺失要素二:硬件
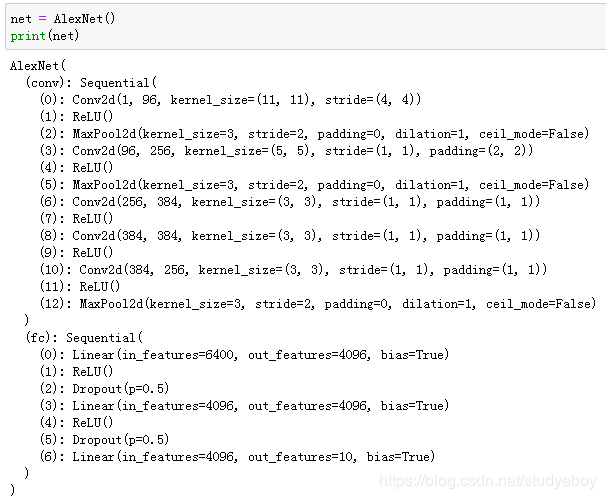
AlexNet


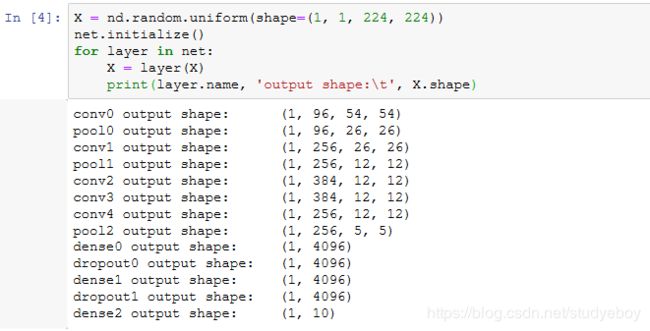
构造一个高和宽均为224的单通道数据样本来观察每一层的输出形状。
读取数据
虽然论文中AlexNet使用ImageNet数据集,但因为ImageNet数据集训练时间较长,我们仍用前面的Fashion-MNIST数据集来演示AlexNet。读取数据的时候我们额外做了一步将图像高和宽扩大到AlexNet使用的图像高和宽224。这个可以通过Resize实例来实现。也就是说,我们在ToTensor实例前使用Resize实例,然后使用Compose实例来将这两个变换串联以方便调用。
训练
这时候我们可以开始训练AlexNet了。相对于上一节的LeNet,这里的主要改动是使用了更小的学习率。


小结
- AlexNet跟LeNet结构类似,但使用了更多的卷积层和更大的参数空间来拟合大规模数据集ImageNet。它是浅层神经网络和深度神经网络的分界线。
- 虽然看上去AlexNet的实现比LeNet的实现也就多了几行代码而已,但这个观念上的转变和真正优秀实验结果的产生令学术界付出了很多年。
使用重复元素的网络(VGG)
VGG块
对于给定的感受野(与输出有关的输入图像的局部大小),采用堆积的小卷积核优于采用大的卷积核,因为可以增加网络深度来保证学习更复杂的模式,而且代价还比较小(参数更少)。例如,在VGG中,使用了3个3x3卷积核来代替7x7卷积核,使用了2个3x3卷积核来代替5x5卷积核,这样做的主要目的是在保证具有相同感知视野的条件下,提升网络的深度,在一定程度上提升了神经网络的效果。
VGG网络
VGG-11=5个卷积块(前2块单层卷积,后3块双层卷积)=前2块x单层卷积层+后3块x双层卷积=8个卷积层
![]()

下面我们实现VGG-11。


下面构造一个高和宽均为224的单通道数据样本来观察每一层的输出形状。
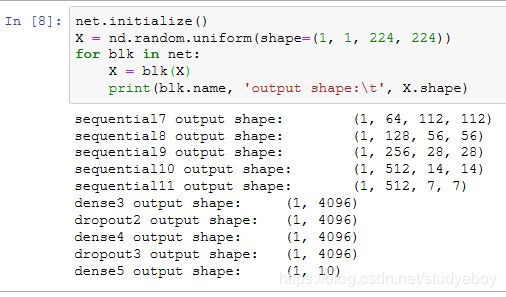


可以看到,每次我们将输入的高和宽减半,直到最终高和宽变成7后传入全连接层。与此同时,输出通道数每次翻倍,直到变成512。因为每个卷积层的窗口大小一样,所以每层的模型参数尺寸和计算复杂度与输入高、输入宽、输入通道数和输出通道数的乘积成正比。VGG这种高和宽减半以及通道翻倍的设计使得多数卷积层都有相同的模型参数尺寸和计算复杂度。
获取数据和训练模型
因为VGG-11计算上比AlexNet更加复杂,出于测试的目的我们构造一个通道数更小,或者说更窄的网络在Fashion-MNIST数据集上进行训练。

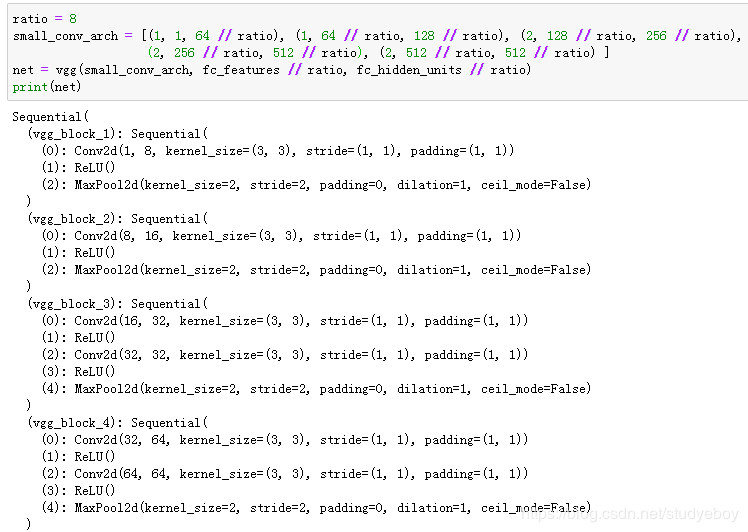

除了使用了稍大些的学习率,模型训练过程与上一节的AlexNet中的类似。
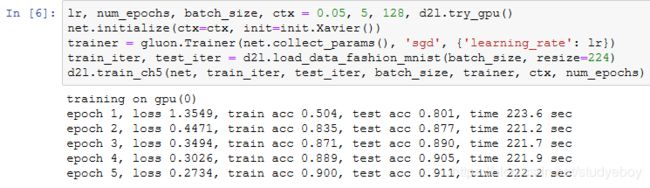
小结
- VGG-11通过5个可以重复使用的卷积块来构造网络。根据每块里卷积层个数和输出通道数的不同可以定义出不同的VGG模型。
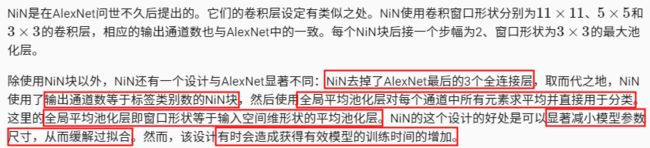
网络中的网络(NiN)
NiN块
NiN模型
获取数据和训练模型
我们依然使用Fashion-MNIST数据集来训练模型。NiN的训练与AlexNet和VGG的类似,但这里使用的学习率更大。
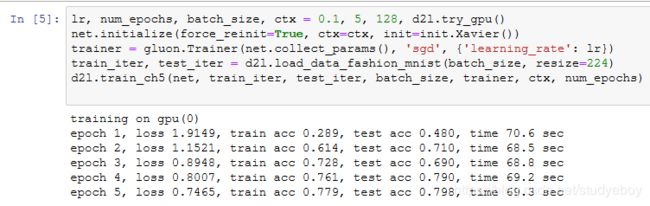
小结
- NiN重复使用由卷积层和代替全连接层的 1×1 卷积层构成的NiN块来构建深层网络。
- NiN去除了容易造成过拟合的全连接输出层,而是将其替换成输出通道数等于标签类别数的NiN块和全局平均池化层。
- NiN的以上设计思想影响了后面一系列卷积神经网络的设计。
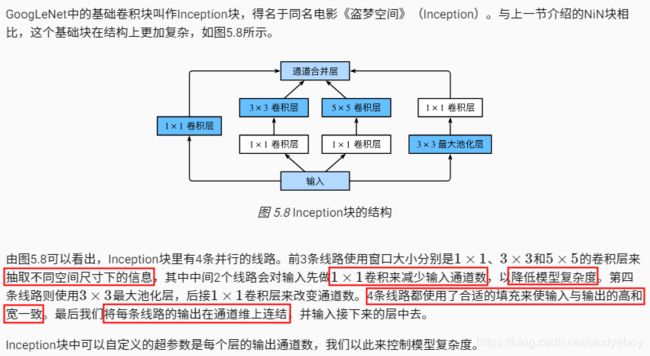
含并行连接的网络(GoogLeNet)
Inception块
GoogLeNet模型
获取数据和训练模型
我们使用高和宽均为96像素的图像来训练GoogLeNet模型。训练使用的图像依然来自Fashion-MNIST数据集。
![]()
![]()
小结
- Inception块相当于一个有4条线路的子网络。它通过不同个窗口形状的卷积层和最大池化层来并行抽取信息,并使用1x1卷积层减少通道数从而降低模型复杂度。
- GoogLeNet将多个设计精细的Inception块和其他层串联起来。其中Inception块的通道数分配之比是在ImageNet数据集上通过大量的实验得来的。
- GoogLeNet和它的后继者们一度是ImageNet上最高效的模型之一:在类似的测试精度下,它们的计算复杂度往往更低。
批量归一化
批量归一化层
对全连接层和卷积层做批量归一化的方法稍有不同。下面我们将分别介绍这两种情况下的批量归一化。
对全连接层做批量归一化
对卷积层做批量归一化
预测时的批量归一化
从零开始实现
下面我们通过NDArray来实现批量归一化层。

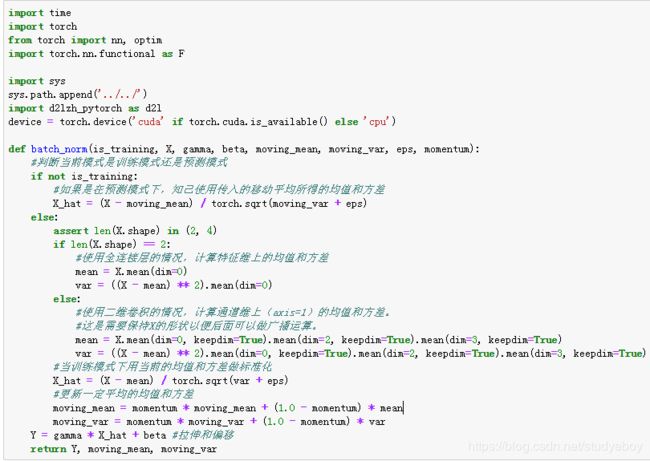
接下来,我们自定义一个BatchNorm层。它保存参与求梯度和迭代的拉伸参数gamma和偏移参数beta,同时也维护移动平均得到的均值和方差,以便能够在模型预测时被使用。BatchNorm实例所需指定的num_features参数对于全连接层来说应为输出个数,对于卷积层来说则为输出通道数。该实例所需指定的num_dims参数对于全连接层和卷积层来说分别为2和4。

![]()
使用批量归一化层的LeNet
下面修改卷积神经网络LeNet模型,从而应用批量归一化层。在所有的卷积层或全连接层之后、激活层之前加入批量归一化层。


下面训练修改后的模型。


最后查看第一个批量归一化层学习到的拉伸参数gamma和偏移参数beta。


简洁实现
与我们刚刚自己定义的BatchNorm类相比,Gluon中nn模块定义的BatchNorm类使用起来更加简单。它不需要指定自己定义的BatchNorm类中所需的num_features和num_dims参数值。在Gluon中,这些参数值都将通过延后初始化而自动获取。下面我们用Gluon实现使用批量归一化的LeNet。
![]()
![]()
使用同样的超参数进行训练。
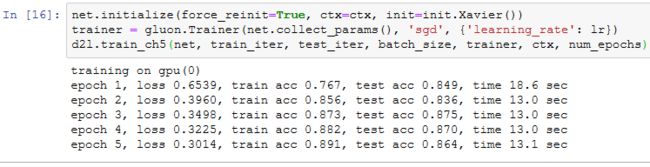

小结
- 在模型训练时,批量归一化利用小批量上的均值和标准差,不断调整神经网络的中间输出,从而使整个神经网络在各层的中间输出的数值更稳定。
- 对全连接层和卷积层批量归一化的方法稍有不同。
- 批量归一化层和丢弃层一样,在训练模式和预测模式的计算结果不一样的。
- Gluon提供的BatchNorm类使用起来简单、方便。
残差网络(ResNet)
残差块
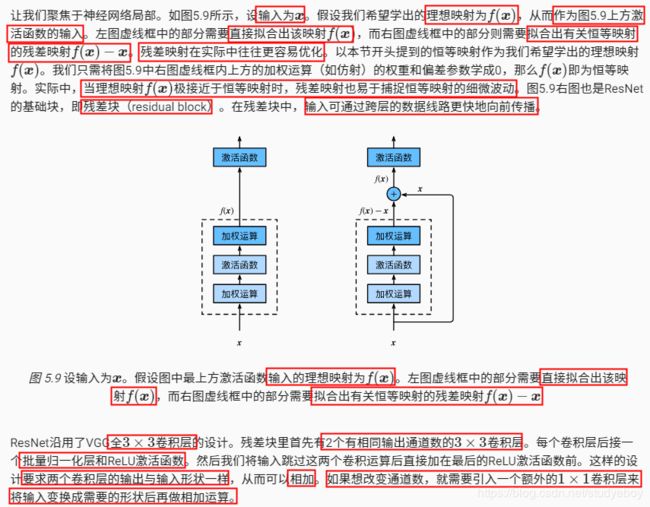
残差块的实现如下。它可以设定输出通道数、是否使用额外的 1×1 卷积层来修改通道数以及卷积层的步幅。
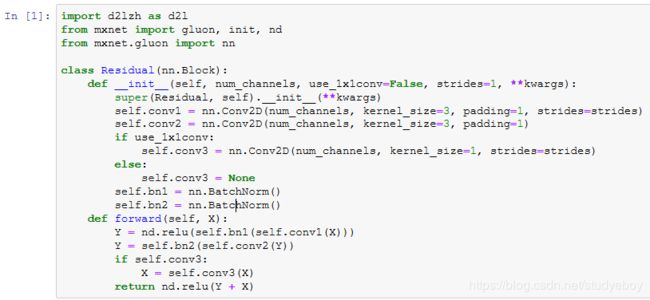

下面我们来查看输入和输出形状一致的情况。

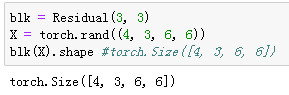
我们也可以在增加输出通道数的同时减半输出的高和宽。

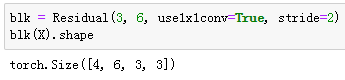
ResNet模型
![]()

![]()


接着我们为ResNet加入所有残差块。这里每个模块使用两个残差块。

![]()
最后,与GoogLeNet一样,加入全局平均池化层后接上全连接层输出。
![]()


在训练ResNet之前,我们来观察一下输入形状在ResNet不同模块之间的变化。


获取数据和训练模型
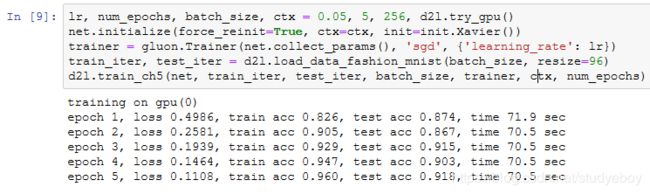
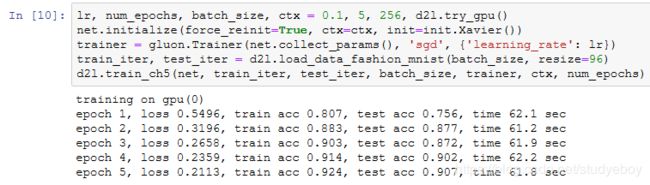
下面我们在Fashion-MNIST数据集上训练ResNet。

小结
- 残差块通过跨层的数据通道从而能够训练处有效的深度神经网络。
- ResNet深刻影响了后来的深度神经网络的设计。
稠密连接网络(DenseNet)
![]()
稠密块
DenseNet使用了ResNet改良版的“批量归一化、激活和卷积”结构,我们首先在conv_block函数里实现这个结构。

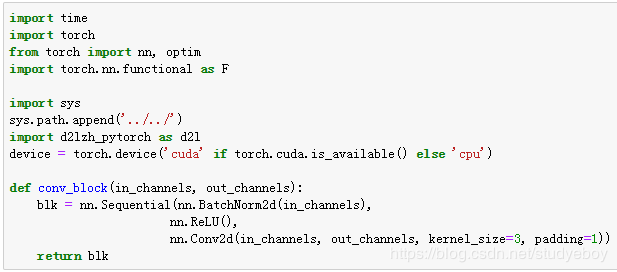
稠密块由多个conv_block组成,每块使用相同的输出通道数。但在前向计算时,我们将每块的输入和输出在通道维上连结。





过渡层
由于每个稠密块都会带来通道数的增加,使用过多则会带来过于复杂的模型。过渡层用来控制模型复杂度。它通过 1×1 卷积层来减小通道数,并使用步幅为2的平均池化层减半高和宽,从而进一步降低模型复杂度。

对上一个例子中稠密块的输出使用通道数为10的过渡层。此时输出的通道数减为10,高和宽均减半。

![]()
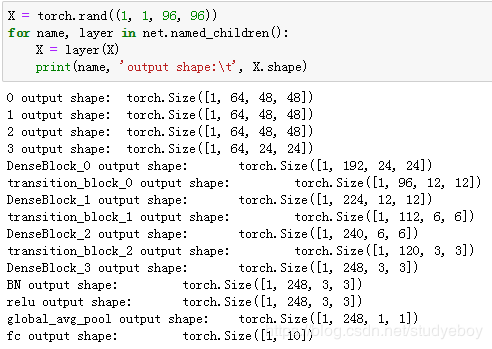
DenseNet模型
我们来构造DenseNet模型。DenseNet首先使用同ResNet一样的单卷积层和最大池化层。
![]()




同ResNet一样,最后接上全局池化层和全连接层来输出。


在训练DenseNet之前,我们来观察一下输入形状在DenseNet不同模块之间的变化。


获取数据并训练模型
由于这里使用了比较深的网络,本节里我们将输入高和宽从224降到96来简化计算。

小结
- 在跨层连接上,不同于ResNet中将输入与输出相加,DenseNet在通道维上连接输入与输出。
- DenseNet的主要构件模块是稠密块和过渡块。
循环神经网络
语言模型
语言模型的计算
n元语法
小结
- 语言模型是自然语言处理的重要技术。
- N 元语法是基于n−1阶马尔可夫链的概率语言模型,其中n权衡了计算复杂度和模型准确性。
循环神经网络
不含隐藏状态的神经网络
含隐藏状态的循环神经网络
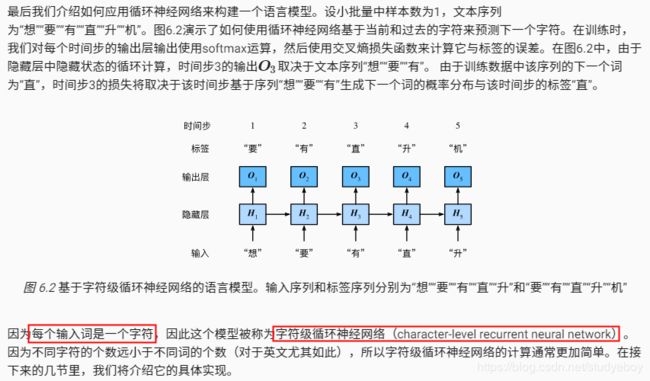
应用:基于字符级循环神经网络的语言模型
小结
- 使用循环计算的网络即循环神经网络
- 循环神经网络的隐藏层状态可以捕捉截至当前时间步的序列的历史信息。
- 循环神经网络模型参数的数量不随时间步长的增加而增长。
- 可以基于字符级循环神经网络来创建语言模型。
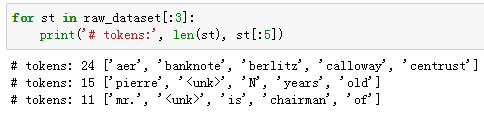
语言模型数据集(周杰伦专辑歌词)
读取数据集
首先读取这个数据集,看看前40个字符是什么样的。

![]()
这个数据集有6万多个字符。为了打印方便,我们把换行符替换成空格,然后仅使用前1万个字符来训练模型。


建立字符索引
我们将每个字符映射成一个从0开始的连续整数,又称索引,来方便之后的数据处理。为了得到索引,我们将数据集里所有不同字符取出来,然后将其逐一映射到索引来构造词典。接着,打印vocab_size,即词典中不同字符的个数,又称词典大小。


之后,将训练数据集中每个字符转化为索引,并打印前20个字符及其对应的索引。


我们将以上代码封装在d2lzh包里的load_data_jay_lyrics函数中,以方便后面章节调用。调用该函数后会依次得到corpus_indices、char_to_idx、idx_to_char和vocab_size这4个变量。
时序数据的采样
![]()
随机采样



让我们输入一个从0到29的连续整数的人工序列。设批量大小和时间步数分别为2和6。打印随机采样每次读取的小批量样本的输入X和标签Y。可见,相邻的两个随机小批量在原始序列上的位置不一定相毗邻。


相邻采样

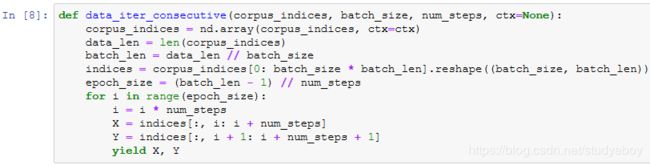

同样的设置下,打印相邻采样每次读取的小批量样本的输入X和标签Y。相邻的两个随机小批量在原始序列上的位置相毗邻。


小结
- 时序数据采样方法包括随机采样和相邻采样。使用这两种方式的循环神经网络训练在实现上略有不同。
循环神经网络的从零开始实现
从零开始实现一个基于字符级循环神经网络的语言模型,并在周杰伦专辑歌词数据集上训练一个模型来进行歌词创作。首先,读取周杰伦专辑歌词数据集:


one-hot向量
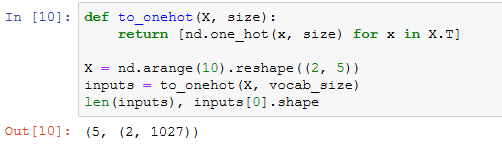
为了将词表示成向量输入到神经网络,一个简单的办法是使用one-hot向量。假设词典中不同字符的数量为 N (即词典大小vocab_size),每个字符已经同一个从0到 N−1 的连续整数值索引一一对应。如果一个字符的索引是整数 i , 那么我们创建一个全0的长为 N 的向量,并将其位置为 i 的元素设成1。该向量就是对原字符的one-hot向量。下面分别展示了索引为0和2的one-hot向量,向量长度等于词典大小。





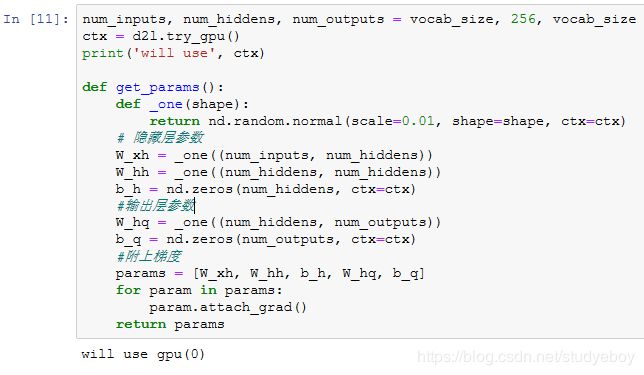
初始化模型参数
接下来,我们初始化模型参数。隐藏单元个数 num_hiddens是一个超参数。

定义模型
根据循环神经网络的计算表达式实现该模型。首先定义init_rnn_state函数来返回初始化的隐藏状态。它返回由一个形状为**(批量大小, 隐藏单元个数)**的值为0的NDArray组成的元组。使用元组是为了更便于处理隐藏状态含有多个NDArray的情况。

![]()
下面的rnn函数定义了在一个时间步里如何计算隐藏状态和输出。这里的激活函数使用了tanh函数。当元素在实数域上均匀分布时,tanh函数值的均值为0。


做个简单的测试来观察输出结果的个数(时间步数),以及第一个时间步的输出层输出的形状和隐藏状态的形状。

![]()
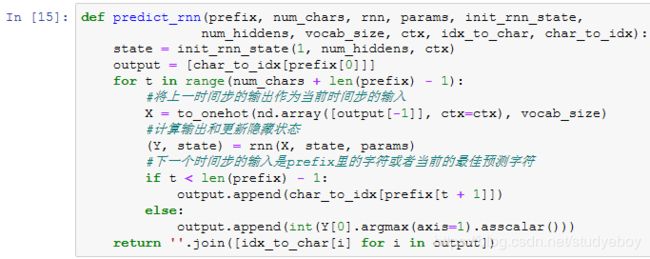
定义预测函数
以下函数基于前缀prefix(含有数个字符的字符串)来预测接下来的num_chars个字符。这个函数稍显复杂,其中我们将循环神经单元rnn设置成了函数参数,这样能重复使用这个函数。

先测试一下predict_rnn函数。将根据前缀“分开”创作长度为10个字符(不考虑前缀长度)的一段歌词。因为模型参数为随机值,所以预测结果也是随机的。



裁剪梯度
困惑度
定义模型训练函数
训练模型并创作歌词
现在我们可以训练模型了。首先,设置模型超参数。我们将根据前缀“分开”和“不分开”分别创作长度为50个字符(不考虑前缀长度)的一段歌词。我们每过50个迭代周期便根据当前训练的模型创作一段歌词。


下面采用随机采样训练模型并创作歌词。


接下来采用相邻采样训练模型并创作歌词。


小结
- 可以使用基于字符级循环神经网络的语言模型来生成文本序列,例如创作歌词。
- 当训练循环神经网络时,为了应对梯度爆炸,可以裁剪梯度。
- 困惑度是对交叉熵损失函数做指数运算后得到的值。
循环神经网络的简洁实现
定义模型
Gluon的rnn模块提供了循环神经网络的实现。下面构造一个含单隐藏层、隐藏单元个数为256的循环神经网络层rnn_layer,并对权重做初始化。


接下来调用rnn_layer的成员函数begin_state来返回初始化的隐藏状态列表。它有一个形状为**(隐藏层个数, 批量大小, 隐藏单元个数)**的元素。




![]()
接下来我们继承Block类来定义一个完整的循环神经网络。它首先将输入数据使用one-hot向量表示后输入到rnn_layer中,然后使用全连接输出层得到输出。输出个数等于词典大小vocab_size。


训练模型
同上一节一样,下面定义一个预测函数。这里的实现区别在于前向计算和初始化隐藏状态的函数接口。


让我们使用权重为随机值的模型来预测一次。


接下来实现训练函数。算法同上一节的一样,但这里只使用了相邻采样来读取数据。


使用和上一节实验中一样的超参数来训练模型。


小结
- Gluon的rnn模块提供了循环神经网络层的实现。
- Gluon的rnn.RNN实例在前向计算后会分别返回输出和隐藏状态。该前向计算并不涉及输出层计算。
通过时间反向传播
![]()
定义模型
模型计算图
方法
小结
- 通过时间反向传播是反向传播在循环神经网络中的具体应用。
- 当时间步数较大或者时间步较小时,循环神经网络的梯度较容易出现衰减或爆炸。
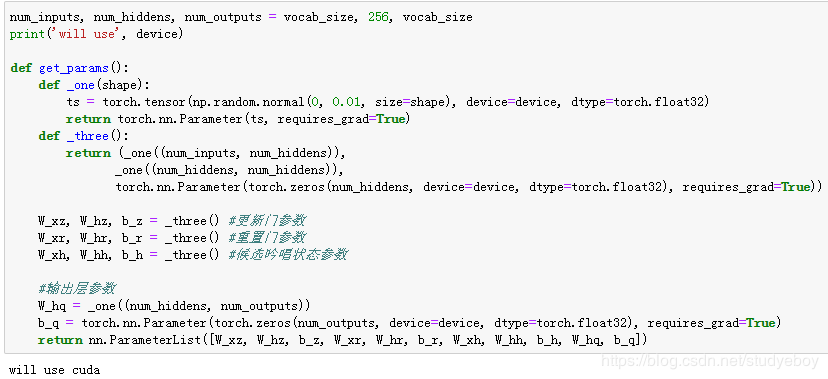
门控循环单元(GRU)
门控循环单元
重置门和更新门
候选隐藏状态
隐藏状态
读取数据集
为了实现并展示门控循环单元,下面依然使用周杰伦歌词数据集来训练模型作词。

从零开始实现
初始化模型参数
下面的代码对模型参数进行初始化。超参数num_hiddens定义了隐藏单元的个数。

定义模型
下面的代码定义隐藏状态初始化函数init_gru_state。它返回由一个形状为(批量大小, 隐藏单元个数)的值为0的NDArray组成的元组。
![]()

下面根据门控循环单元的计算表达式定义模型。


训练模型并创作歌词
我们在训练模型时只使用相邻采样。设置好超参数后,我们将训练模型并根据前缀“分开”和“不分开”分别创作长度为50个字符的一段歌词。

![]()
我们每过40个迭代周期便根据当前训练的模型创作一段歌词。


简洁实现
小结
- 门控循环神经网络可以更好的捕捉时间序列中的时间步距离较大的依赖关系。
- 门控循环单元引入了门的概念,从而修改了循环神经网络中隐藏状态的计算方式。它包括重置门、更新门、候选隐藏状态和隐藏状态。
- 重置门有助于捕捉时间序列里短期的依赖关系。
- 更新门有助于捕捉时间序列里长期的依赖关系。
长短期记忆(LSTM)
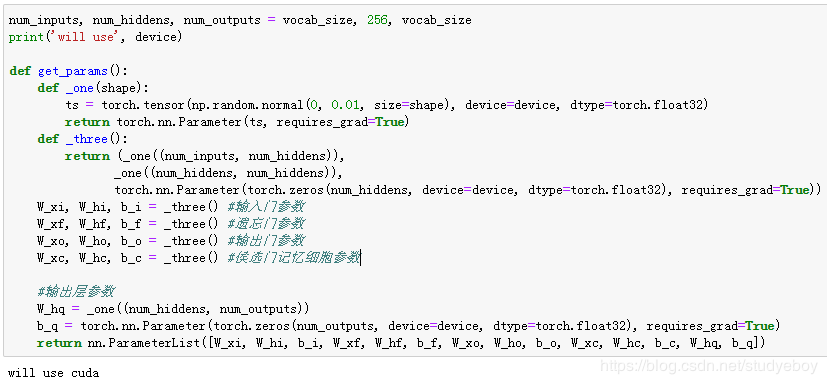
长短期记忆(long short-term memory,LSTM)是另一种常见的门控循环神经网络。它比门控循环单元的结构稍微复杂一点。
长短期记忆
LSTM 中引入了3个门,即输入门(input gate)、遗忘门(forget gate)和输出门(output gate),以及与隐藏状态形状相同的记忆细胞(某些文献把记忆细胞当成一种特殊的隐藏状态),从而记录额外的信息。
输入门、遗忘门、和输出门
候选记忆细胞
记忆细胞
隐藏状态
读取数据集
下面我们开始实现并展示长短期记忆。这里依然使用周杰伦歌词数据集来训练模型作词。

从零开始实现
初始化模型参数
下面的代码对模型参数进行初始化。超参数num_hiddens定义了隐藏单元的个数。

定义模型
在初始化函数中,长短期记忆的隐藏状态需要返回额外的形状为(批量大小, 隐藏单元个数)的值为0的记忆细胞。


下面根据长短期记忆的计算表达式定义模型。需要注意的是,只有隐藏状态会传递到输出层,而记忆细胞不参与输出层的计算。
![]()

训练模型并创作歌词
我们在训练模型时只使用相邻采样。设置好超参数后,我们将训练模型并根据前缀“分开”和“不分开”分别创作长度为50个字符的一段歌词。


我们每过40个迭代周期便根据当前训练的模型创作一段歌词。


简洁实现
小结
- 长短记忆的隐藏层输出包括隐藏层状态和记忆细胞。只有隐藏层状态会传递到输出层。
- 长短记忆的输入门、遗忘门和输出门可以控制信息的流动。
- 长短记忆可以应对循环神经网络中的梯度衰减问题,并更好的捕捉时间序列中时间步距离较大的依赖关系。
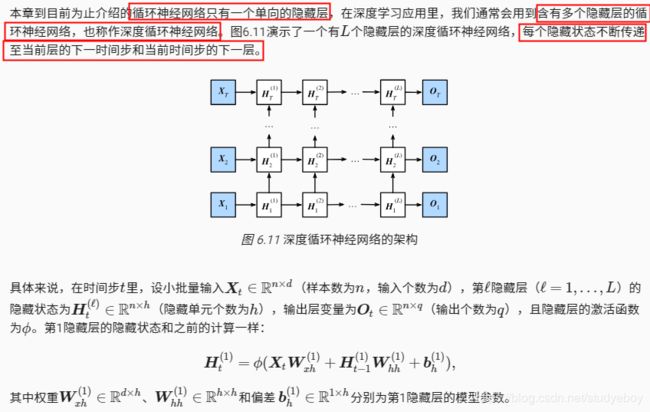
深度循环神经网络
小结
- 在深度循环神经网络中,隐藏状态的信息不断传递至当前层的下一时间步和当前时间步的下一层。
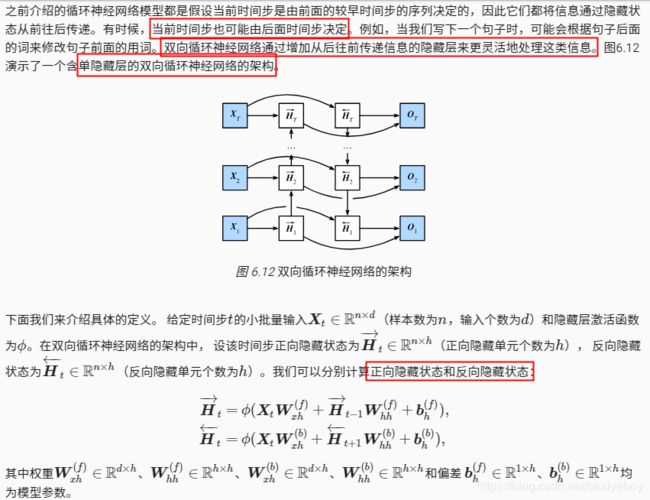
双向循环神经网络
小结
- 双向循环神经网络在每个时间步的隐藏状态同时取决于该时间步之前和之后的子序列(包括当前时间步的输入)。
优化算法
优化与深度学习
优化与深度学习的关系
优化在深度学习中的挑战
局部最小值
鞍点
小结
- 由于优化算法的目标函数通常是一个基于训练数据集的损失函数,优化的目标在于降低训练误差。
- 由于深度学习模型参数通常都是高维的,目标函数的鞍点通常比局部最小值更常见。
梯度下降和随机梯度下降
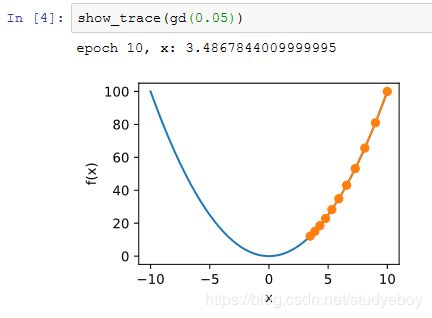
一维梯度下降


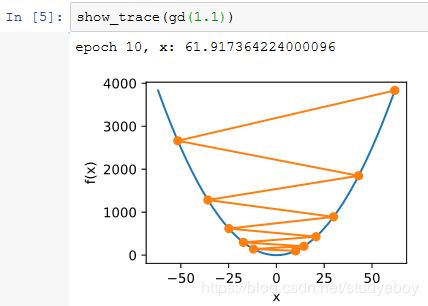
接下来使用 x=10 作为初始值,并设 η=0.2 。使用梯度下降对 x 迭代10次,可见最终 x 的值较接近最优解。

下面将绘制出自变量 x 的迭代轨迹。

学习率
多维梯度下降

![]()

然后,观察学习率为 0.1 时自变量的迭代轨迹。使用梯度下降对自变量 x 迭代20次后,可见最终 x 的值较接近最优解 [0,0] 。

随机梯度下降

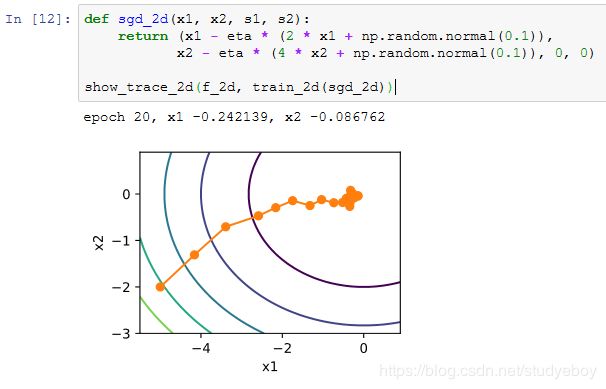
可以看到,随机梯度下降中自变量的迭代轨迹相对于梯度下降中的来说更为曲折。这是由于实验所添加的噪声使模拟的随机梯度的准确度下降。在实际中,这些噪声通常指训练数据集中的无意义的干扰。
小结
- 使用适当的学习率,沿着梯度反方向更新自变量可能降低目标函数值。梯度下降重复这一更新过程直到得到满足要求的解。
- 学习率过大或过小都有问题。一个合适的学习率通常是需要通过多次实验找到的。
- 当训练数据集的样本较多时,梯度下降每次迭代的计算开销较大,因而随机梯度下降通常更受青睐。
小批量随机梯度下降
读取数据
我们将使用一个来自NASA的测试不同飞机机翼噪音的数据集来比较各个优化算法 [1]。我们使用该数据集的前1,500个样本和5个特征,并使用标准化对数据进行预处理。

从零开始实现



下面实现一个通用的训练函数,以方便本章后面介绍的其他优化算法使用。它初始化一个线性回归模型,然后可以使用小批量随机梯度下降以及后续小节介绍的其他算法来训练模型。

当批量大小为样本总数1,500时,优化使用的是梯度下降。梯度下降的1个迭代周期对模型参数只迭代1次。可以看到6次迭代后目标函数值(训练损失)的下降趋向了平稳。


当批量大小为1时,优化使用的是随机梯度下降。为了简化实现,有关(小批量)随机梯度下降的实验中,我们未对学习率进行自我衰减,而是直接采用较小的常数学习率。随机梯度下降中,每处理一个样本会更新一次自变量(模型参数),一个迭代周期里会对自变量进行1,500次更新。可以看到,目标函数值的下降在1个迭代周期后就变得较为平缓。


虽然随机梯度下降和梯度下降在一个迭代周期里都处理了1,500个样本,但实验中随机梯度下降的一个迭代周期耗时更多。这是因为随机梯度下降在一个迭代周期里做了更多次的自变量迭代,而且单样本的梯度计算难以有效利用矢量计算。
当批量大小为10时,优化使用的是小批量随机梯度下降。它在每个迭代周期的耗时介于梯度下降和随机梯度下降的耗时之间。
![]()
![]()
简洁实现
在Gluon里可以通过创建Trainer实例来调用优化算法。这能让实现更简洁。下面实现一个通用的训练函数,它通过优化算法的名字trainer_name和超参数trainer_hyperparams来创建Trainer实例。


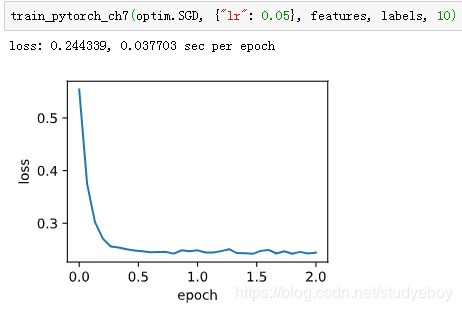
使用Gluon重复上一个实验。

小结
- 小批量随机梯度每次随机均匀采样一个小批量的训练样本来计算梯度。
- 在实际中(小批量)随机梯度下降的学习率可以在迭代过程中自我衰减。
- 通常小批量随机梯度在每个迭代周期的耗时介于梯度下降和随机梯度下降的耗时之间。
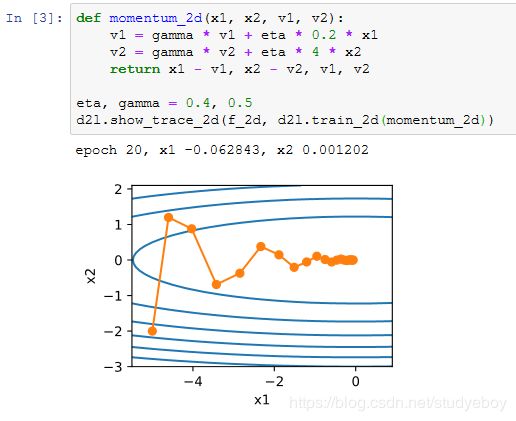
动量法
![]()
梯度下降的问题
动量法
指数加权移动平均
由指数加权移动平均理解动量法
从零开始实现
相对于小批量随机梯度下降,动量法需要对每一个自变量维护一个同它一样形状的速度变量,且超参数里多了动量超参数。实现中,我们将速度变量用更广义的状态变量states表示。
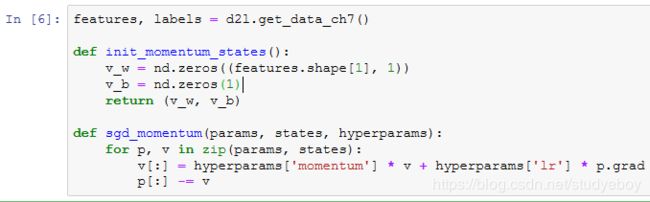

我们先将动量超参数momentum设0.5,这时可以看成是特殊的小批量随机梯度下降:其小批量随机梯度为最近2个时间步的2倍小批量梯度的加权平均。
![]()
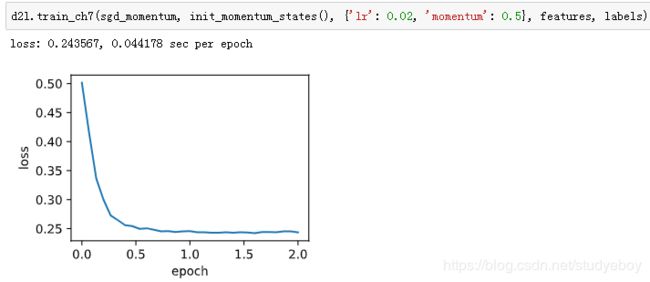
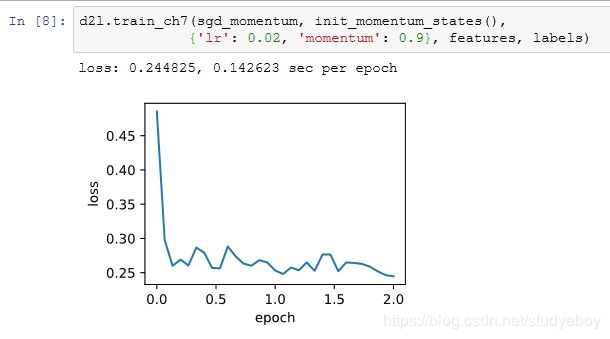
将动量超参数momentum增大到0.9,这时依然可以看成是特殊的小批量随机梯度下降:其小批量随机梯度为最近10个时间步的10倍小批量梯度的加权平均。我们先保持学习率0.02不变。
![]()
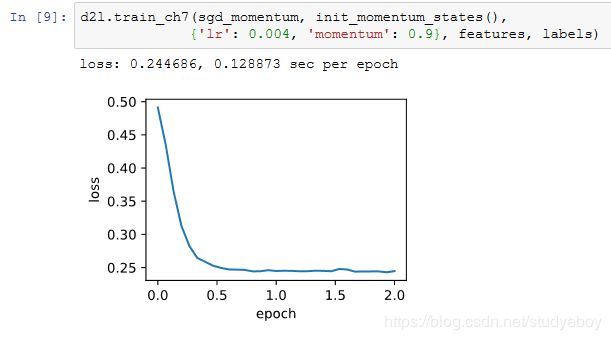
可见目标函数值在后期迭代过程中的变化不够平滑。直觉上,10倍小批量梯度比2倍小批量梯度大了5倍,我们可以试着将学习率减小到原来的1/5。此时目标函数值在下降了一段时间后变化更加平滑。

简洁实现
在Gluon中,只需要在Trainer实例中通过momentum来指定动量超参数即可使用动量法。
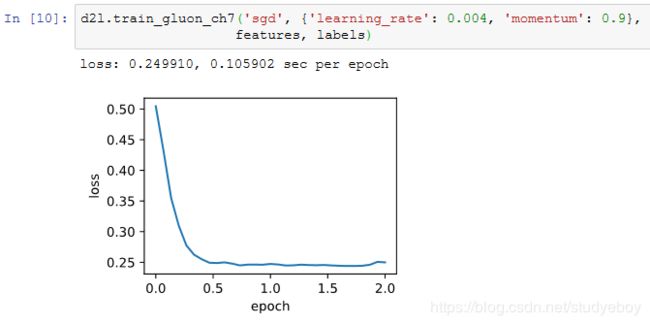
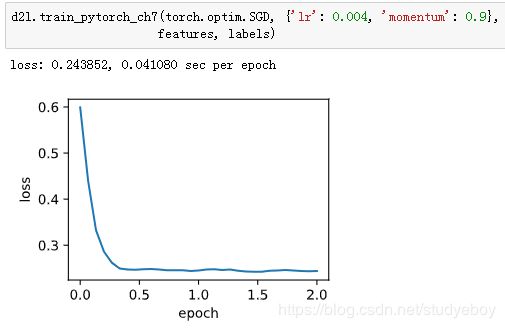
小结
- 动量法使用了指数加权移动平均的思路。它将过去时间步的梯度做了加权平均,且权重按时间步指定数衰减。
- 动量法使得相邻时间步的自变量更新在方向上更加一致。
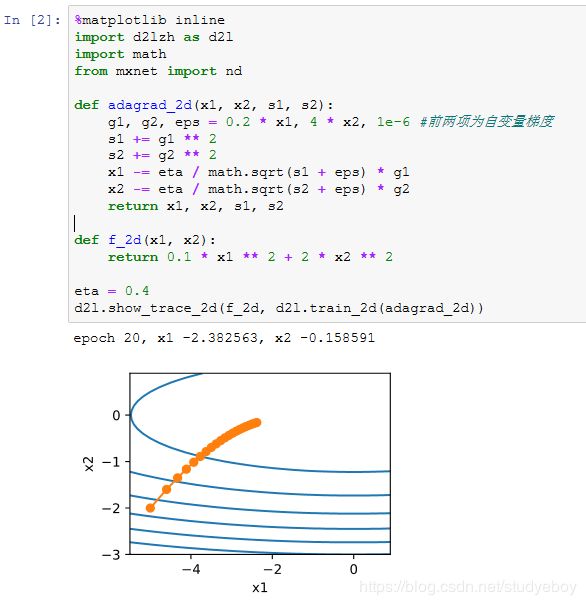
AdaGrad算法
算法
特点

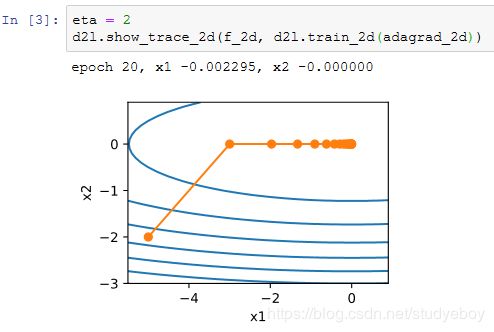
下面将学习率增大到2。可以看到自变量更为迅速地逼近了最优解。
从零开始实现
同动量法一样,AdaGrad算法需要对每个自变量维护同它一样形状的状态变量。我们根据AdaGrad算法中的公式实现该算法。


与“小批量随机梯度下降”一节中的实验相比,这里使用更大的学习率来训练模型。
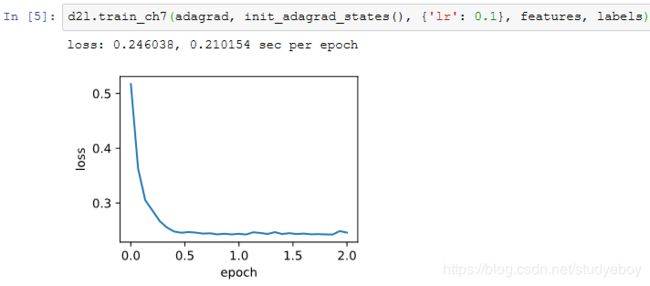

简洁实现
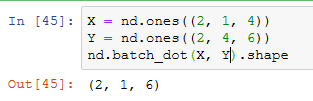
通过名称为“adagrad”的Trainer实例,我们便可使用Gluon提供的AdaGrad算法来训练模型。


小结
- AdaGrad算法在迭代过程中不断调整学习率,并让目标函数自变量中每个元素都分别拥有自己的学习率。
- 使用AdaGrad算法时,自变量中每个元素的学习率在迭代过程中一直在降低(或不变)。
RMSProp算法
算法
从零开始实现
接下来按照RMSProp算法中的公式实现该算法。


我们将初始学习率设为0.01,并将超参数 γ γ γ 设为0.9。此时,变量 s t s_t st 可看作是最近 1/(1−0.9)=10 个时间步的平方项 g t ⊙ g t g_t⊙g_t gt⊙gt 的加权平均。
![]()
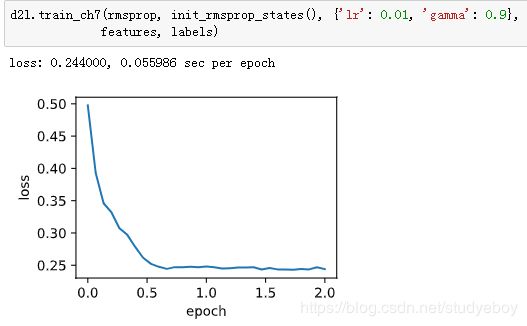
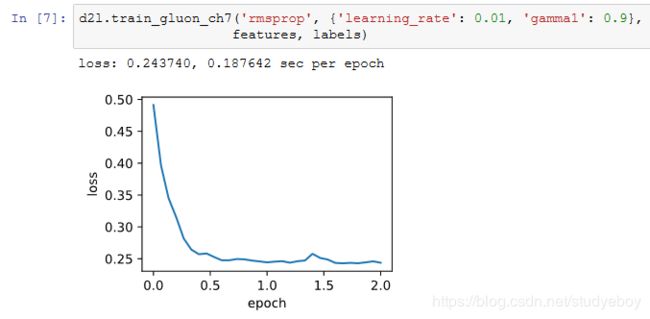
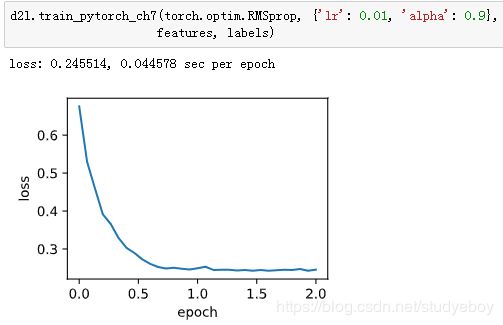
简洁实现
通过名称为“rmsprop”的Trainer实例,我们便可使用Gluon提供的RMSProp算法来训练模型。注意,超参数 γ 通过gamma1指定。
小结
- RMSProp算法和AdaGrad算法的不同在于,RMSProp算法使用了小批量随机梯度按元素平方的指数加权移动平均来调整学习率。
AdaDelta算法
算法
从零开始实现
AdaDelta算法需要对每个自变量维护两个状态变量,即 s t s_t st和 Δ x t Δx_t Δxt。我们按AdaDelta算法中的公式实现该算法。
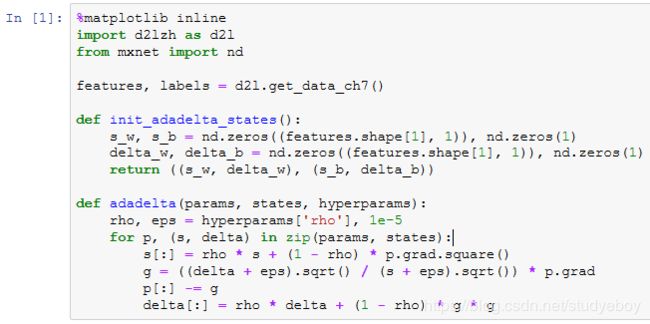
使用超参数 ρ = 0.9 ρ=0.9 ρ=0.9 来训练模型。
![]()
![]()
简洁实现
通过名称为“adadelta”的Trainer实例,我们便可使用Gluon提供的AdaDelta算法。它的超参数可以通过rho来指定。
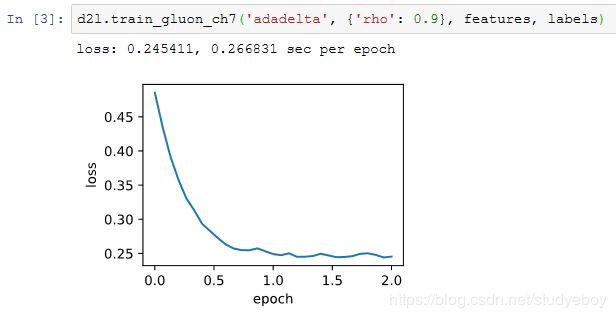

小结
- AdaDelta算法没有学习率超参数,它通过使用有关自变量更新量平方的指数加权移动平均的项来替代RMSProp算法中的学习率。
Adam算法
Adam算法在RMSProp算法基础上对小批量随机梯度也做了指数加权移动平均 。下面我们来介绍这个算法。
算法
从零开始实现
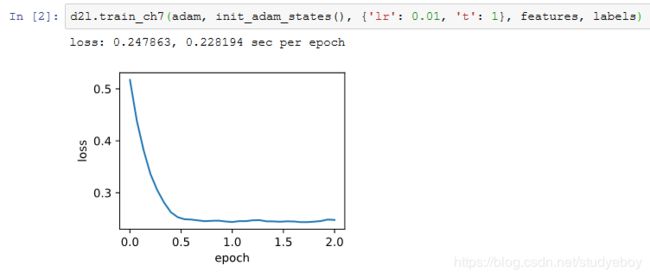
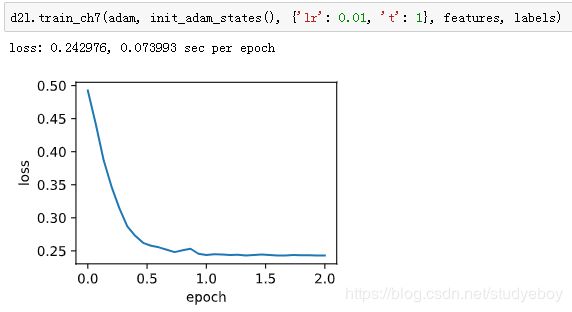
我们按照Adam算法中的公式实现该算法。其中时间步 t 通过hyperparams参数传入adam函数。


使用学习率为0.01的Adam算法来训练模型。
简洁实现
通过名称为“adam”的Trainer实例,我们便可使用Gluon提供的Adam算法。
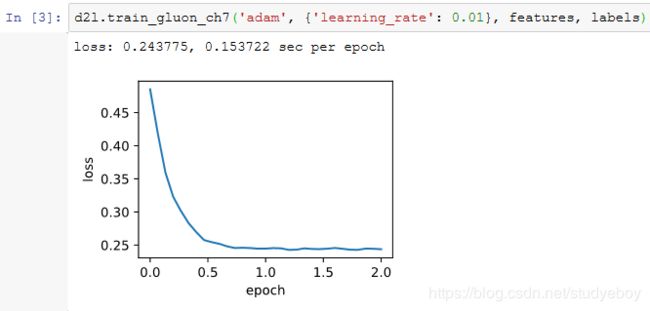

小结
- Adam算法在RMSProp算法的基础上对小批量随机梯度也做了指数加权移动平均。
- Adam算法使用了偏差修正。
计算性能
在深度学习中,数据集通常很大而且模型计算往往很复杂。因此,我们十分关注计算性能。本章将重点介绍影响计算性能的重要因子:命令式编程、符号式编程、异步计算、自动并行计算和多GPU计算。通过本章的学习,你将很可能进一步提升前几章已实现的模型的计算性能,例如,在不影响模型精度的前提下减少模型的训练时间。
命令式和符号式混合编程
混合式编程取两者之长
使用HybridSequential类构造模型
Sequential类用来串联多个层。为了使用混合式编程,将Sequential类替换成HybridSequential类。
通过调用hybridize函数来编译和优化HybridSequential实例中串联的层的计算。模型的计算结果不变。
需要注意的是,只有继承HybridBlock类的层才会被优化计算。例如,HybridSequential类和Gluon提供的Dense类都是HybridBlock类的子类,它们都会被优化计算。如果一个层只是继承自Block类而不是HybridBlock类,那么它将不会被优化。
计算性能
下面通过比较调用hybridize函数前后的计算时间来展示符号式编程的性能提升。这里我们对1000次net模型计算计时。在net调用hybridize函数前后,它分别依据命令式编程和符号式编程做模型计算。
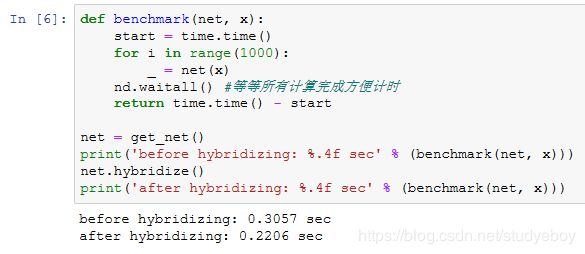
由上述结果可见,在一个HybridSequential实例调用hybridize函数后,它可以通过符号式编程提升计算性能。
获取符号式程序
在模型net根据输入计算模型输出后,例如benchmark函数中的net(x),我们就可以通过export函数将符号式程序和模型参数保存到硬盘。
![]()
![]()


使用HybridBlock类构造模型



![]()
再运行一次前向计算会得到同样的结果。
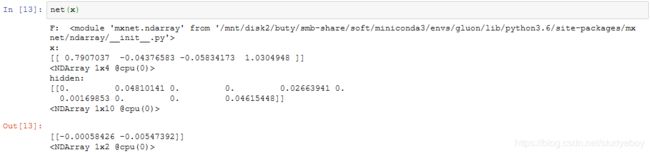
接下来看看调用hybridize函数后会发生什么。

可以看到,F变成了Symbol。而且,虽然输入数据还是NDArray,但在hybrid_forward函数里,相同输入和中间输出全部变成了Symbol类型。
再运行一次前向计算看看。


小结
- 命令式编程和符号式编程各有优劣。MXNet通过混合式编程取二者之长。
- 通过HybridSequential类和HybridBlock类构建的模型可以调用hybridize函数将命令式程序转成符号式程序。建议大家使用这种方法获得计算性能的提升。
异步计算
MXNet使用异步计算来提升计算性能。理解它的工作原理既有助于开发更高效的程序,又有助于在内存资源有限的情况下主动降低计算性能从而减小内存开销。我们先导入本节中实验需要的包或模块。
MXNet中的异步计算
用同步函数让前端等待计算结果


下面是使用waitall函数的例子。输出用时包含了变量y和变量z的计算时间。

此外,任何将NDArray转换成其他不支持异步计算的数据结构的操作都会让前端等待计算结果。例如,当我们调用asnumpy函数和asscalar函数时:


![]()
使用异步计算提升计算性能
异步计算对内存的影响


下面定义多层感知机、优化算法和损失函数。

这里定义辅助函数来监测内存的使用。需要注意的是,这个函数只能在Linux或macOS上运行。

现在我们可以做测试了。我们先试运行一次,让系统把net的参数初始化。

对于训练模型net来说,我们可以自然地使用同步函数asscalar将每个小批量的损失从NDArray格式中取出,并打印每个迭代周期后的模型损失。此时,每个小批量的生成间隔较长,不过内存开销较小。
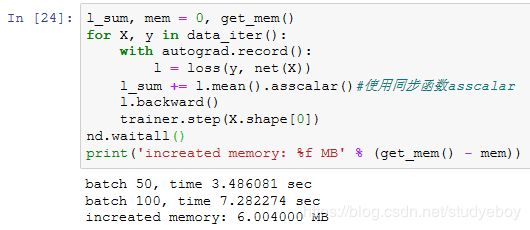
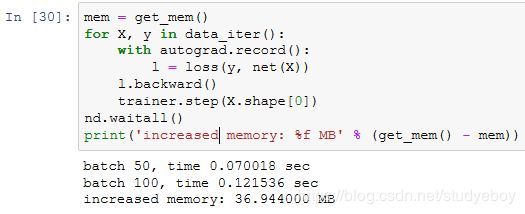
如果去掉同步函数,虽然每个小批量的生成间隔较短,但训练过程中可能会导致内存占用较高。这是因为在默认异步计算下,前端会将所有小批量计算在短时间内全部丢给后端。这可能在内存积压大量中间结果无法释放。实验中我们看到,不到一秒,所有数据(X和y)就都已经产生。但因为训练速度没有跟上,所以这些数据只能放在内存里不能及时清除,从而占用额外内存。
小结
- MXNet包括用户直接用来交互的前端和系统用来执行计算的后端。
- MXNet能够通过异步计算提升计算性能。
- 建议使用每个小批量训练或预测时至少使用一个同步函数,从而避免在短时间内将过多计算任务丢给后端。
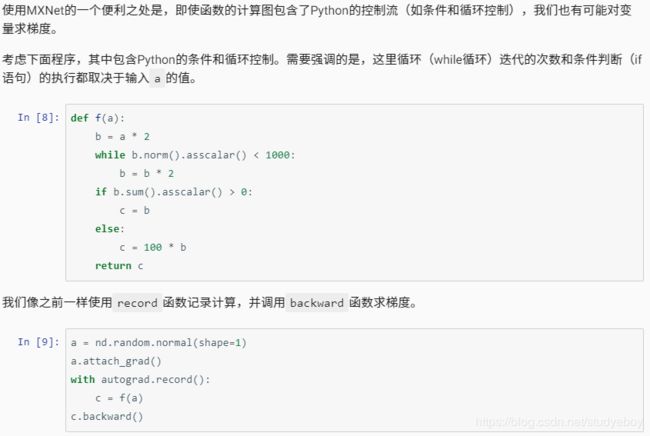
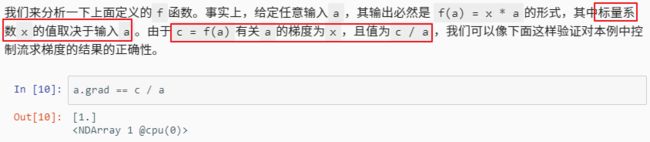
自动并行计算
CPU和GPU的并行计算
CPU和GPU的并行计算,例如,程序中的计算既发生在CPU上,又发生在GPU上。先定义run函数,令它做10次矩阵乘法。
![]()
接下来,分别在内存和显存上创建NDArray。
![]()
然后,分别使用它们在CPU和GPU上运行run函数并打印运行所需时间。
![]()
我们去掉run(x_cpu)和run(x_gpu)这两个计算任务之间的waitall同步函数,并希望系统能自动并行这两个任务。

可以看到,当两个计算任务一起执行时,执行总时间小于它们分开执行的总和。这表明,MXNet能有效地在CPU和GPU上自动并行计算。
计算和通信的并行计算
在同时使用CPU和GPU的计算中,经常需要在内存和显存之间复制数据,造成数据的通信。在下面的例子中,我们在GPU上计算,然后将结果复制回CPU使用的内存。我们分别打印GPU上计算时间和显存到内存的通信时间。
![]()
我们去掉计算和通信之间的waitall同步函数,打印这两个任务完成的总时间。
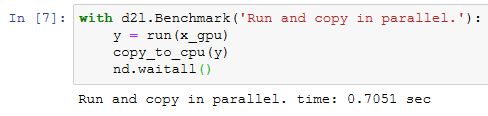

小结
- MXNet能够通过自动并行计算提升计算性能,例如CPU和GPU的并行计算以及计算和通信的并行。
多GPU计算
数据并行
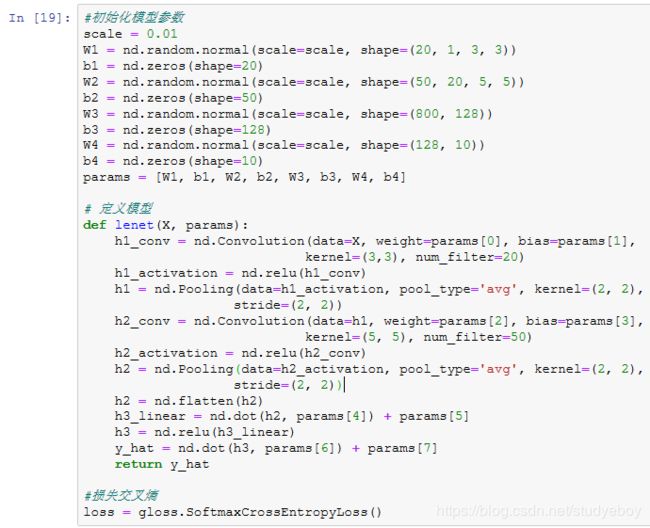
定义模型
LeNet来作为本节的样例模型。这里的模型实现部分只用到了NDArray。
多GPU之间同步数据
我们需要实现一些多GPU之间同步数据的辅助函数。下面的get_params函数将模型参数复制到某块显卡的显存并初始化梯度。

尝试把模型参数params复制到gpu(0)上。
![]()
给定分布在多块显卡的显存之间的数据。下面的allreduce函数可以把各块显卡的显存上的数据加起来,然后再广播到所有的显存上。
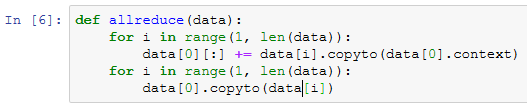
简单测试一下allreduce函数。
![]()
给定一个批量的数据样本,下面的split_and_load函数可以将其划分并复制到各块显卡的显存上。

让我们试着用split_and_load函数将6个数据样本平均分给2块显卡的显存。
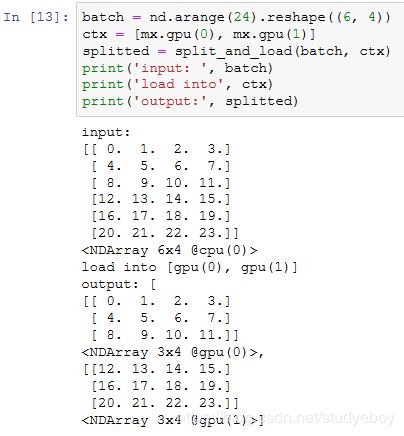
单个小批量上的多GPU训练
现在我们可以实现单个小批量上的多GPU训练了。它的实现主要依据本节介绍的数据并行方法。我们将使用刚刚定义的多GPU之间同步数据的辅助函数allreduce和split_and_load。

定义训练函数
在这里我们需要依据数据并行将完整的模型参数复制到多块显卡的显存上,并在每次迭代时对单个小批量进行多GPU训练。

多GPU训练实验
让我们先从单GPU训练开始。设批量大小为256,学习率为0.2。
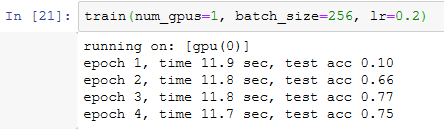
保持批量大小和学习率不变,将使用的GPU数量改为2。可以看到,测试精度的提升同上一个实验中的结果大体相当。因为有额外的通信开销,所以我们并没有看到训练时间的显著降低。因此,我们将在下一节实验计算更加复杂的模型。
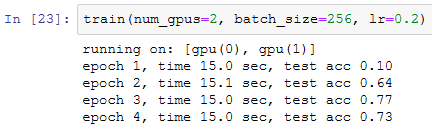
小结
- 可以使用数据并行更充分地利用多块GPU的计算资源,实现多GPU训练模型。
- 给定超参数的情况下,改变GPU数量时模型的训练精度大体相当。
多GPU计算的简洁实现
多GPU上初始化模型参数
多GPU训练模型
![]()
首先在单GPU上训练模型。
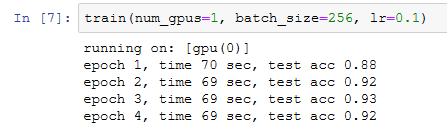
然后尝试在2块GPU上训练模型。与上一节使用的LeNet相比,ResNet-18的计算更加复杂,通信时间比计算时间更短,因此ResNet-18的并行计算所获得的性能提升更佳。

小结
- 在Gluon中,可以很方便地进行多GPU计算,例如,在多GPU及相应的显存上初始化模型参数和训练模型。
多GPU计算(PyTorch)
计算机视觉
图像增广
常用的图像增广方法
读取一张形状为 400×500 (高和宽分别为400像素和500像素)的图像作为实验的样例。


下面定义绘图函数show_images。

大部分图像增广方法都有一定的随机性。为了方便观察图像增广的效果,定义一个辅助函数apply。这个函数对输入图像img多次运行图像增广方法aug并展示所有的结果。

翻转和裁剪
左右翻转图像通常不改变物体的类别。它是最早也是最广泛使用的一种图像增广方法。下面我们通过transforms模块创建RandomFlipLeftRight实例来实现一半概率的图像左右翻转。


上下翻转不如左右翻转通用。但是至少对于样例图像,上下翻转不会造成识别障碍。下面我们创建RandomFlipTopBottom实例来实现一半概率的图像上下翻转。





变化颜色
![]()
![]()

类似地,我们也可以随机变化图像的色调。


我们也可以创建RandomColorJitter实例并同时设置如何随机变化图像的亮度(brightness)、对比度(contrast)、饱和度(saturation)和色调(hue)。



叠加多个图像增广方法
实际应用中我们会将多个图像增广方法叠加使用。我们可以通过Compose实例将上面定义的多个图像增广方法叠加起来,再应用到每张图像之上。
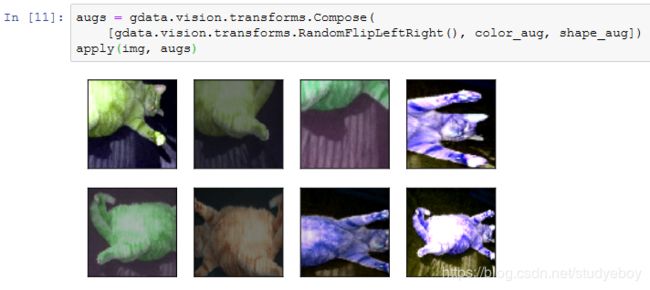

使用图像增广训练模型
使用多GPU训练模型


下面定义的辅助函数_get_batch将小批量数据样本batch划分并复制到ctx变量所指定的各个显存上。


接下来,我们定义train函数使用多GPU训练并评价模型。


现在就可以定义train_with_data_aug函数使用图像增广来训练模型了。该函数获取了所有可用的GPU,并将Adam算法作为训练使用的优化算法,然后将图像增广应用于训练数据集之上,最后调用刚才定义的train函数训练并评价模型。


下面使用随机左右翻转的图像增广来训练模型。
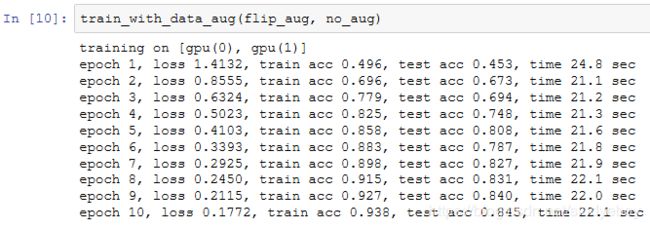
![]()
小结
- 图像增广基于现有训练数据生成随机图像从而应对过拟合。
- 为了在预测时得到确定的结果,通常只将图像增广应用在训练样本上,而不在预测时使用含随机操作的图像增广。
- 可以从Gluon的transforms模块中获取有关图片增广的类。
微调
热狗识别
获取数据集


我们创建两个ImageFolderDataset实例来分别读取训练数据集和测试数据集中的所有图像文件。


下面画出前8张正类图像和最后8张负类图像。可以看到,它们的大小和高宽比各不相同。
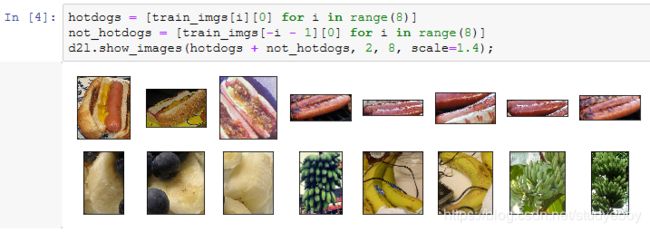
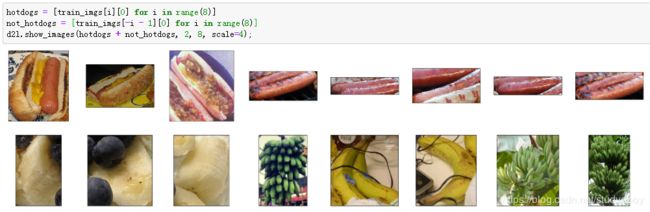
![]()
![]()

定义和初始化模型
我们使用在ImageNet数据集上预训练的ResNet-18作为源模型。这里指定pretrained=True来自动下载并加载预训练的模型参数。在第一次使用时需要联网下载模型参数。
![]()

![]()

![]()
![]()
![]()

微调模型
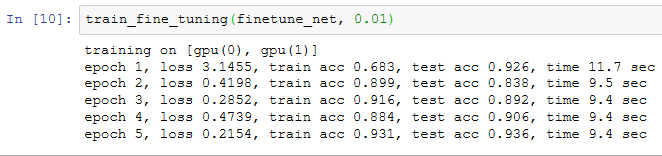
我们先定义一个使用微调的训练函数train_fine_tuning以便多次调用。


我们将Trainer实例中的学习率设得小一点,如0.01,以便微调预训练得到的模型参数。根据前面的设置,我们将以10倍的学习率从头训练目标模型的输出层参数。
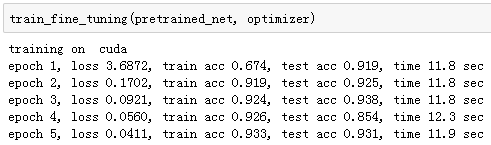
作为对比,我们定义一个相同的模型,但将它的所有模型参数都初始化为随机值。由于整个模型都需要从头训练,我们可以使用较大的学习率。
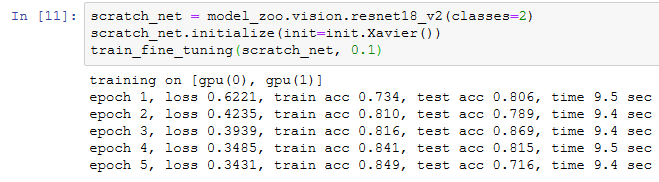

可以看到,微调的模型因为参数初始值更好,往往在相同迭代周期下取得更高的精度。
小结
- 迁移学习将从源数据集学到的知识迁移到目标数据集上。微调是迁移学习的一种常用技术。
- 目标模型复制了源模型上除了输出层外的所有模型设计及其参数,并基于目标数据集微调这些参数。而目标模型的输出层需要从头训练。
- 一般来说,微调参数会使用较小的学习率,而从头训练输出层可以使用较大的学习率。
目标检测和边界框


下面加载本节将使用的示例图像。可以看到图像左边是一只狗,右边是一只猫。它们是这张图像里的两个主要目标。

边界框
![]()
![]()
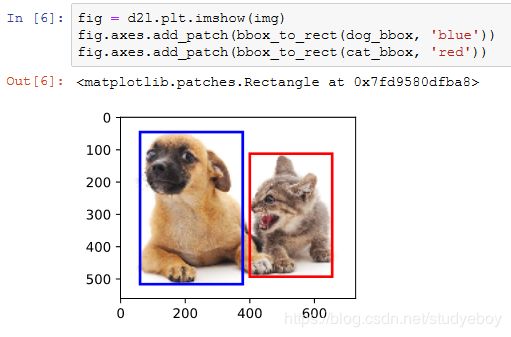
我们可以在图中将边界框画出来,以检查其是否准确。画之前,我们定义一个辅助函数bbox_to_rect。它将边界框表示成matplotlib的边界框格式。

我们将边界框加载在图像上,可以看到目标的主要轮廓基本在框内。
小结
- 在目标检测里不仅需要找出图像里面所有感兴趣的目标,而且要知道它们的位置。位置一般由矩形边界框来表示。
锚框
生成多个锚框

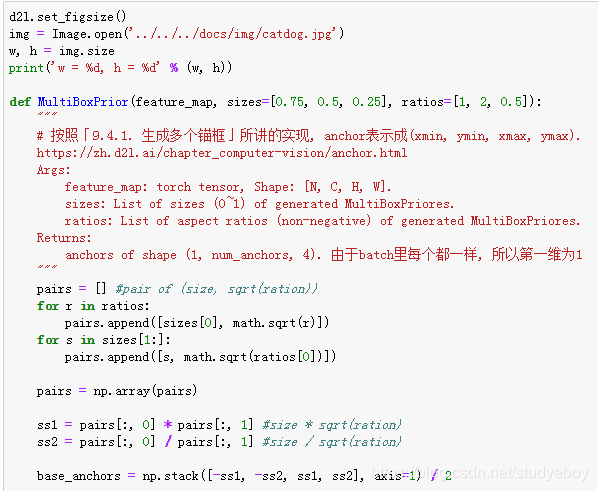






为了描绘图像中以某个像素为中心的所有锚框,我们先定义show_bboxes函数以便在图像上画出多个边界框。




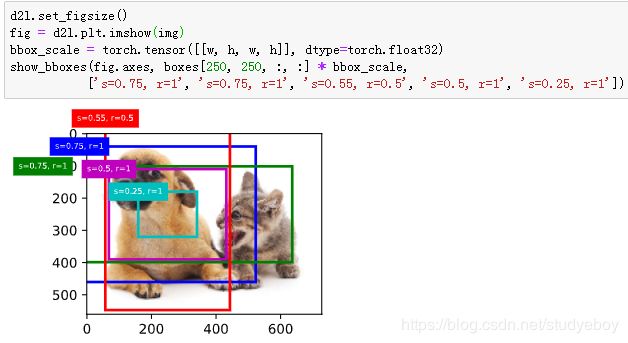
交并比
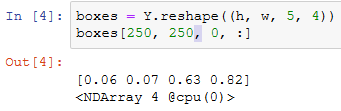
标注训练集的锚框

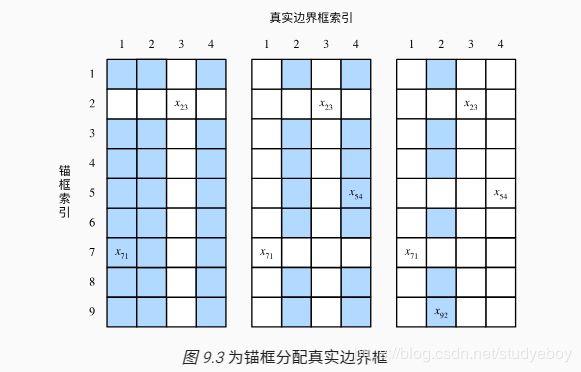




![]()



![]()

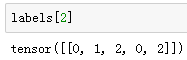
返回的结果里有3项,均为NDArray。第三项表示为锚框标注的类别。
![]()
![]()


返回的第一项是为每个锚框标注的四个偏移量,其中负类锚框的偏移量标注为0。

![]()
输出预测边界框



在图像上打印预测边界框和它们的置信度。

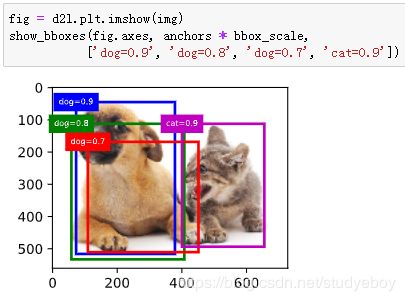






我们移除掉类别为-1的预测边界框,并可视化非极大值抑制保留的结果。
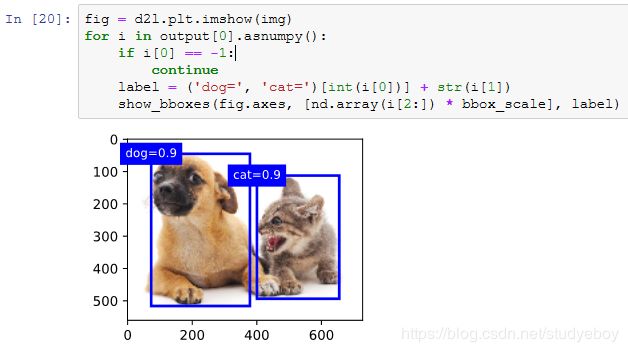

![]()
小结
- 以每个像素为中心,生成多个大小和宽高比不同的锚框。
- 交并比是两个边界框相交面积与相并面积之比。
- 在训练集中,为每个锚框标注两类标签:一是锚框所含目标的类别;二是真实边界框相对锚框的偏移量。
- 预测时,可以使用非极大值抑制来移除相似的预测边界框,从而令结果简洁。
多尺度目标检测

![]()

![]()

![]()
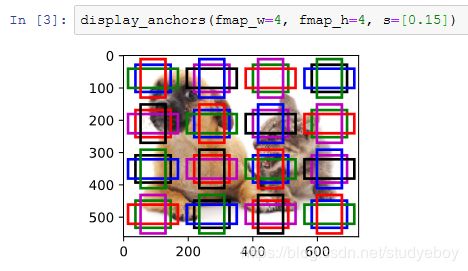

我们将特征图的高和宽分别减半,并用更大的锚框检测更大的目标。当锚框大小设0.4时,有些锚框的区域有重合。


最后,我们将特征图的高和宽进一步减半至1,并将锚框大小增至0.8。此时锚框中心即图像中心。

![]()

小结
- 可以在多个尺度下生成不同数量和不同大小的锚框,从而在多个尺度下检测不同大小的目标。
- 特征图的形状能确定任一图像上均匀采样的锚框中心。
- 用输入图像在某个感受野区域内的信息来预测输入图像上与该区域相近的锚框的类别和偏移量。
目标检测数据集(皮卡丘)
下载数据集
RecordIO格式的皮卡丘数据集可以直接在网上下载。下载数据集的操作定义在_download_pikachu函数中。


读取数据集
图示数据
小结
- 合成的皮卡丘数据集可用于测试目标检测模型。
- 目标检测的数据读取跟图像分类的类似。然而,在引入边界框后,标签形状和图像增广(如随机裁剪)发生了变化。
单发多框检测(SSD)
模型
类别预测层
边界框预测层
连接多尺度的预测
高和宽减半块
基础网络块
完整的模型
训练模型
训练单发多框检测模型来进行目标检测。
读取数据集和初始化
读取“目标检测数据集(皮卡丘)”一节构造的皮卡丘数据集。

在皮卡丘数据集中,目标的类别数为1。定义好模型以后,我们需要初始化模型参数并定义优化算法。

定义损失函数和评价函数


我们可以沿用准确率评价分类结果。因为使用了 L1 范数损失,我们用平均绝对误差评价边界框的预测结果。

训练模型
预测
在预测阶段,我们希望能把图像里面所有我们感兴趣的目标检测出来。下面读取测试图像,将其变换尺寸,然后转成卷积层需要的四维格式。

我们通过MultiBoxDetection函数根据锚框及其预测偏移量得到预测边界框,并通过非极大值抑制移除相似的预测边界框。

最后,我们将置信度不低于0.3的边界框筛选为最终输出用以展示。
![]()
小结
- 单发多框检测是一个多尺度的目标检测模型。该模型基于基础网络块和各个多尺度特征块生成不同数量和不同大小的锚框,并通过预测锚框的类别和偏移量检测不同大小的目标。
- 单发多框检测在训练中根据类别和偏移量的预测和标注值计算损失函数。
- 当目标在图像中占比较小时,模型通常会采用比较大的输入图像尺寸。
- 为锚框标注类别时,通常会产生大量的负类锚框。可以对负类锚框进行采样,从而使数据类别更加平衡。这个可以通过设置MultiBoxTarget函数的negative_mining_ratio参数来完成。
- 在损失函数中为有关锚框类别和有关正类锚框偏移量的损失分别赋予不同的权重超参数。
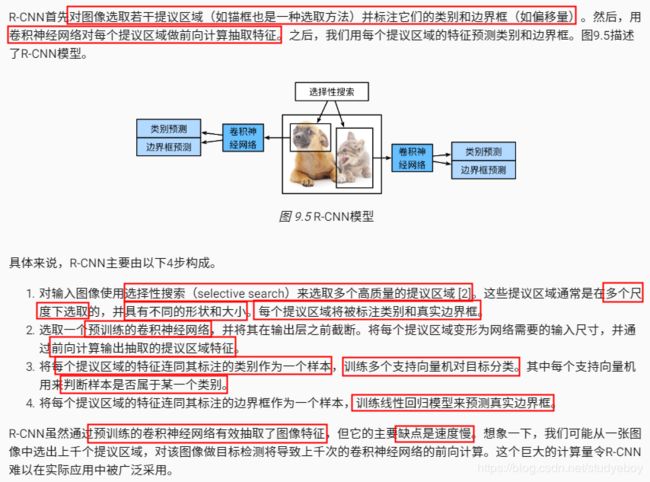
区域卷积神经网络(R-CNN)系列
R-CNN
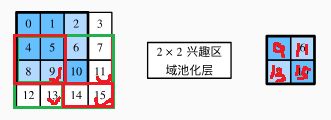
Fast R-CNN

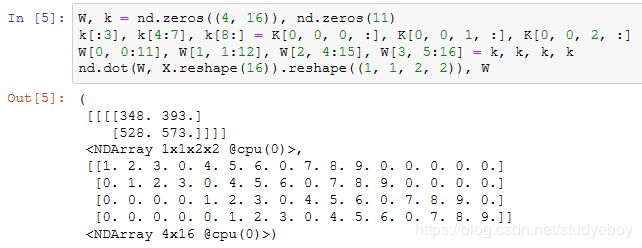
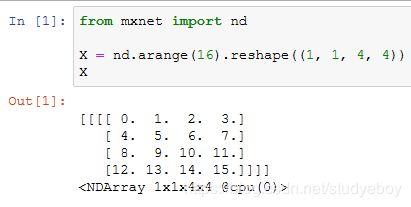
我们使用ROIPooling函数来演示兴趣区域池化层的计算。假设卷积神经网络抽取的特征X的高和宽均为4且只有单通道。

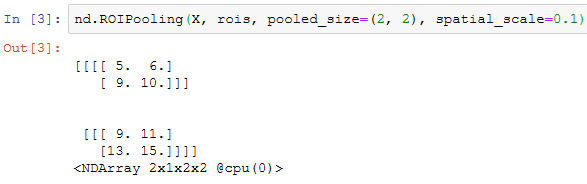
假设图像的高和宽均为40像素。再假设选择性搜索在图像上生成了两个提议区域:每个区域由5个元素表示,分别为区域目标类别、左上角的 x 和 y 轴坐标以及右下角的 x 和 y 轴坐标。
![]()
![]()
由于X的高和宽是图像的高和宽的 1/10 ,以上两个提议区域中的坐标先按spatial_scale自乘0.1,然后在X上分别标出兴趣区域X[:,:,0:3,0:3]和X[:,:,1:4,0:4]。最后对这两个兴趣区域分别划分子窗口网格并抽取高和宽为2的特征。
![]()
Faster R-CNN
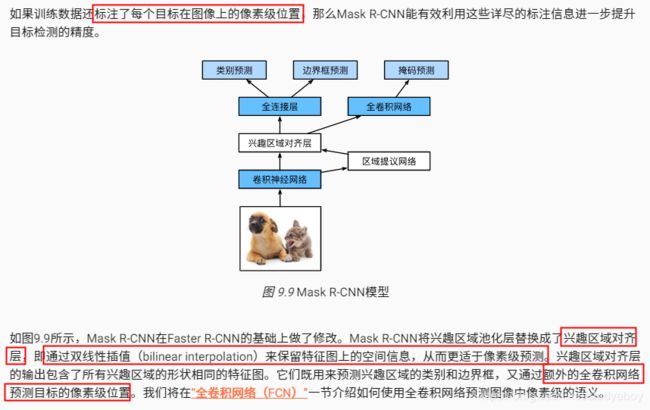
Mask R-CNN
小结
- R-CNN对图像选取若干提议区域,然后用卷积神经网络对每个提议区域做前向计算抽取特征,再用这些特征预测提议区域的类别和边界框。
- Fast R-CNN对R-CNN的一个主要改进在于只对整个图像做卷积神经网络的前向计算。它引入了兴趣区域池化层,从而令兴趣区域能够抽取出形状相同的特征。
- Faster R-CNN将Fast R-CNN中的选择性搜索替换成区域提议网络,从而减少提议区域的生成数量,并保证目标检测的精度。
- Mask R-CNN在Faster R-CNN基础上引入一个全卷积网络,从而借助目标的像素级位置进一步提升目标检测的精度。
语义分割和数据集
图像分割和实例分割
![]()
Pascal VOC2012语义分割数据集
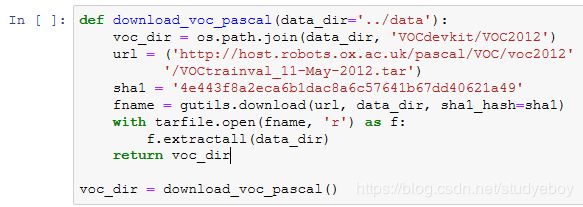
语义分割的一个重要数据集叫作Pascal VOC2012 [1]。为了更好地了解这个数据集,我们先导入实验所需的包或模块。
我们下载这个数据集的压缩包到…/data路径下。压缩包大小是2 GB左右,下载需要一定时间。解压之后的数据集将会放置在…/data/VOCdevkit/VOC2012路径下。

我们画出前5张输入图像和它们的标签。在标签图像中,白色和黑色分别代表边框和背景,而其他不同的颜色则对应不同的类别。

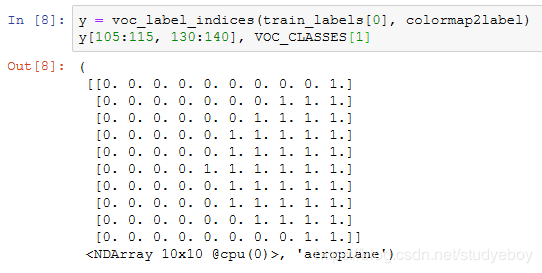
接下来,我们列出标签中每个RGB颜色的值及其标注的类别。

有了上面定义的两个常量以后,我们可以很容易地查找标签中每个像素的类别索引。

例如,第一张样本图像中飞机头部区域的类别索引为1,而背景全是0。
预处理数据
自定义语义分割数据集
读取数据集
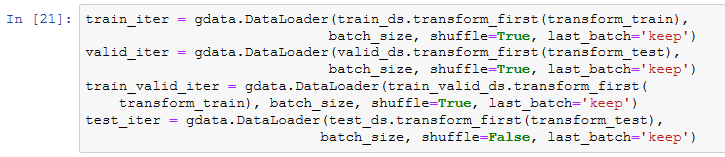
我们通过自定义的VOCSegDataset类来分别创建训练集和测试集的实例。假设我们指定随机裁剪的输出图像的形状为320×480。下面我们可以查看训练集和测试集所保留的样本个数。

设批量大小为64,分别定义训练集和测试集的迭代器。

打印第一个小批量的形状。不同于图像分类和目标识别,这里的标签是一个三维数组。

小结
- 语义分割关注如何将图像分割成属于不同语义类别的区域。
- 语义分割的一个重要数据集叫作Pascal VOC2012。
- 由于语义分割的输入图像和标签在像素上一一对应,所以将图像随机裁剪成固定尺寸而不是缩放。
全卷积网络(FCN)
转置卷积层
构造模型


下面我们创建全卷积网络实例net。它复制了pretrained_net实例成员变量features里除去最后两层的所有层以及预训练得到的模型参数。

给定高和宽分别为320和480的输入,net的前向计算将输入的高和宽减小至原来的 1/32 ,即10和15。



初始化转置卷积层

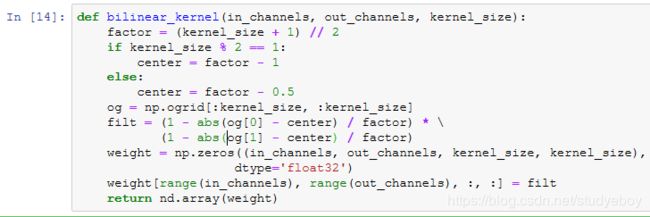
我们来实验一下用转置卷积层实现的双线性插值的上采样。构造一个将输入的高和宽放大2倍的转置卷积层,并将其卷积核用bilinear_kernel函数初始化。

读取图像X,将上采样的结果记作Y。为了打印图像,我们需要调整通道维的位置。

可以看到,转置卷积层将图像的高和宽分别放大2倍。值得一提的是,除了坐标刻度不同,双线性插值放大的图像和“目标检测和边界框”一节中打印出的原图看上去没什么两样。

在全卷积网络中,我们将转置卷积层初始化为双线性插值的上采样。对于 1×1 卷积层,我们采用Xavier随机初始化。

读取数据集
我们用上一节介绍的方法读取数据集。这里指定随机裁剪的输出图像的形状为 320×480 :高和宽都可以被32整除。

训练模型
预测像素类别
在预测时,我们需要将输入图像在各个通道做标准化,并转成卷积神经网络所需要的四维输入格式。
![]()
为了可视化每个像素的预测类别,我们将预测类别映射回它们在数据集中的标注颜色。


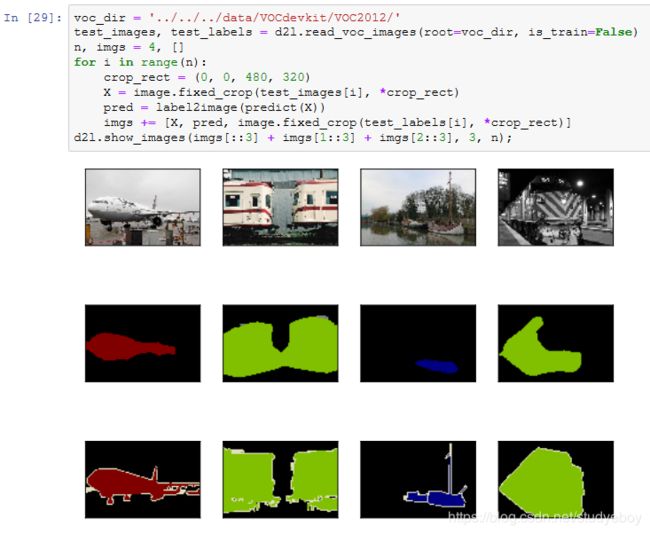
小结
- 可以通过矩阵乘法来实现卷积运算。
- 全卷积网络先使用卷积神经网络抽取图像特征,然后通过 1×1 卷积层将通道数变换为类别个数,最后通过转置卷积层将特征图的高和宽变换为输入图像的尺寸,从而输出每个像素的类别。
- 在全卷积网络中,可以将转置卷积层初始化为双线性插值的上采样。
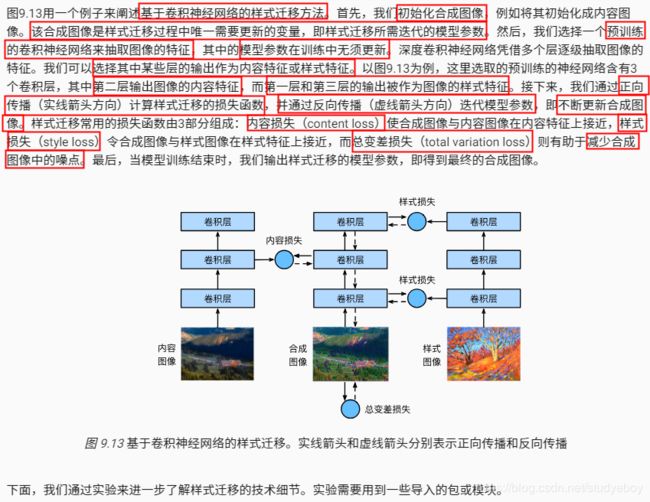
样式迁移
方法
读取内容图像和样式图像
首先,我们分别读取内容图像和样式图像。从打印出的图像坐标轴可以看出,它们的尺寸并不一样。


预处理后处理图像
抽取特征
我们使用基于ImageNet数据集预训练的VGG-19模型来抽取图像特征 。
![]()

![]()

在抽取特征时,我们只需要用到VGG从输入层到最靠近输出层的内容层或样式层之间的所有层。下面构建一个新的网络net,它只保留需要用到的VGG的所有层。我们将使用net来抽取特征。

给定输入X,如果简单调用前向计算net(X),只能获得最后一层的输出。由于我们还需要中间层的输出,因此这里我们逐层计算,并保留内容层和样式层的输出。



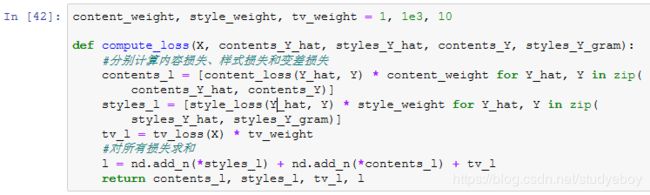
定义损失函数
下面我们来描述样式迁移的损失函数。它由内容损失、样式损失和总变差损失3部分组成。
内容损失
与线性回归中的损失函数类似,内容损失通过平方误差函数衡量合成图像与内容图像在内容特征上的差异。平方误差函数的两个输入均为extract_features函数计算所得到的内容层的输出。

样式损失


自然地,样式损失的平方误差函数的两个格拉姆矩阵输入分别基于合成图像与样式图像的样式层输出。这里假设基于样式图像的格拉姆矩阵gram_Y已经预先计算好了。

总变差损失
损失函数
样式迁移的损失函数即内容损失、样式损失和总变差损失的加权和。通过调节这些权值超参数,我们可以权衡合成图像在保留内容、迁移样式以及降噪三方面的相对重要性。
创建和初始化合成图像
在样式迁移中,合成图像是唯一需要更新的变量。因此,我们可以定义一个简单的模型GeneratedImage,并将合成图像视为模型参数。模型的前向计算只需返回模型参数即可。

下面,我们定义get_inits函数。该函数创建了合成图像的模型实例,并将其初始化为图像X。样式图像在各个样式层的格拉姆矩阵styles_Y_gram将在训练前预先计算好。
![]()
训练


下面我们开始训练模型。首先将内容图像和样式图像的高和宽分别调整为150和225像素。合成图像将由内容图像来初始化。
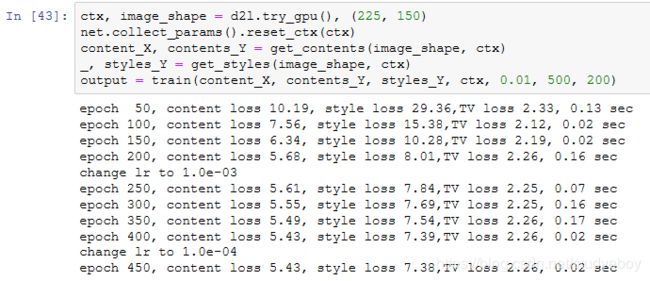
下面我们将训练好的合成图像保存起来。可以看到图9.14中的合成图像保留了内容图像的风景和物体,并同时迁移了样式图像的色彩。因为图像尺寸较小,所以细节上依然比较模糊。
![]()

为了得到更加清晰的合成图像,下面我们在更大的 300×450 尺寸上训练。我们将图9.14的高和宽放大2倍,以初始化更大尺寸的合成图像。
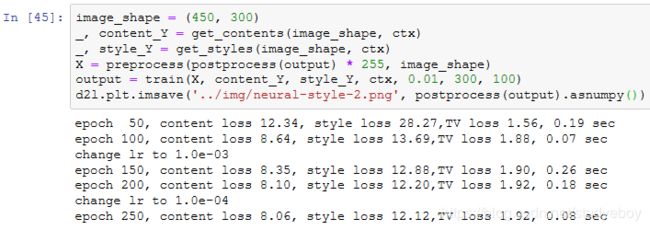
可以看到,由于图像尺寸更大,每一次迭代需要花费更多的时间。从训练得到的图9.15中可以看到,此时的合成图像因为尺寸更大,所以保留了更多的细节。合成图像里面不仅有大块的类似样式图像的油画色彩块,色彩块中甚至出现了细微的纹理。

小结
- 样式迁移常用的损失函数由3部分组成:内容损失使合成图像与内容图像在内容特征上接近,样式损失令合成图像与样式图像在样式特征上接近,而总变差损失则有助于减少合成图像中的噪点。
- 可以通过预训练的卷积神经网络来抽取图像的特征,并通过最小化损失函数来不断更新合成图像。
- 用格拉姆矩阵表达样式层输出的样式。
实战Kaggle比赛:图像分类(CIFAR-10)
获取和整理数据集
下载数据集
解压数据集
整理数据集
![]()
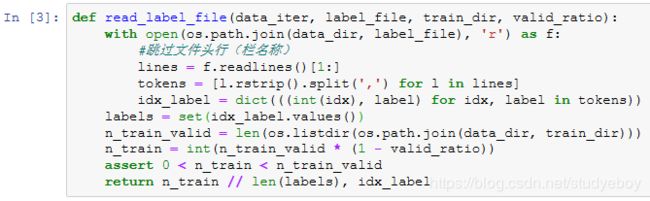
下面定义一个辅助函数,从而仅在路径不存在的情况下创建路径。


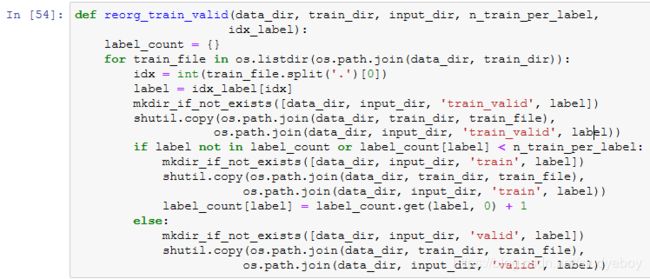
下面的reorg_test函数用来整理测试集,从而方便预测时的读取。

最后,我们用一个函数分别调用前面定义的read_label_file函数、reorg_train_valid函数以及reorg_test函数。



图像增广
读取数据集
定义模型
![]()

下面定义ResNet-18模型。

CIFAR-10图像分类问题的类别个数为10。我们将在训练开始前对模型进行Xavier随机初始化。
![]()
定义训练函数
训练并验证模型
对测试集分类并在Kaggle提交结果
小结
- 可以通过创建ImageFolderDataset实例来读取含原始图像文件的数据集。
- 可以应用卷积神经网络、图像增广和混合式编程来实战图像分类比赛。
实战Kaggle比赛:狗的品种识别(ImageNet Dogs)
获取和整理数据集
下载数据集
整理数据集


下面的reorg_dog_data函数用来读取训练数据标签、切分验证集并整理测试集。
![]()
因为我们在这里使用了小数据集,所以将批量大小设为1。在实际训练和测试时,我们应使用Kaggle比赛的完整数据集并调用reorg_dog_data函数来整理数据集。相应地,我们也需要将批量大小batch_size设为一个较大的整数,如128。

图像增广
本节比赛的图像尺寸比上一节中的更大。这里列举了更多可能有用的图像增广操作。

测试时,我们只使用确定性的图像预处理操作。
![]()
读取数据集
我们创建ImageFolderDataset实例来读取整理后的含原始图像文件的数据集。
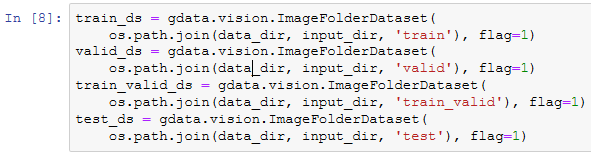
这里创建DataLoader实例的方法也与上一节中的相同。

定义模型


在计算损失时,我们先通过成员变量features来获取预训练模型输出层的输入,即抽取的特征。然后,将该特征作为自定义的小规模输出网络的输入,并计算输出。
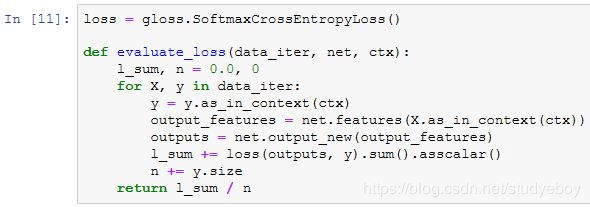
定义训练函数
我们将依赖模型在验证集上的表现来选择模型并调节超参数。模型的训练函数train只训练自定义的小规模输出网络。
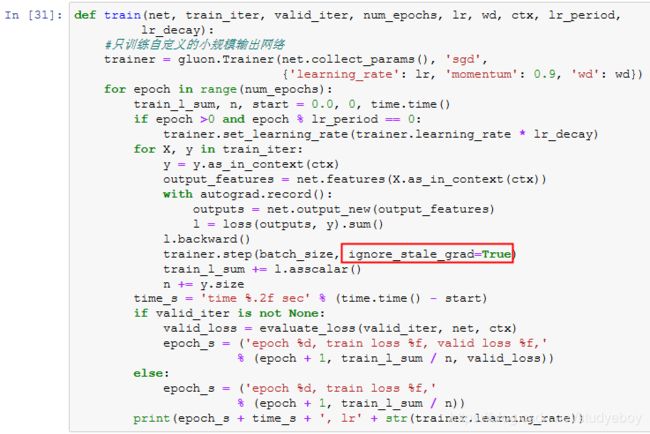
训练并验证模型
现在,我们可以训练并验证模型了。以下超参数都是可以调节的,如增加迭代周期等。由于lr_period和lr_decay分别设为10和0.1,优化算法的学习率将在每10个迭代周期后自乘0.1。
![]()
对测试集分类并在Kaggle提交结果
得到一组满意的模型设计和超参数后,我们使用全部训练数据集(含验证集)重新训练模型,并对测试集分类。注意,我们要用刚训练好的输出网络做预测。
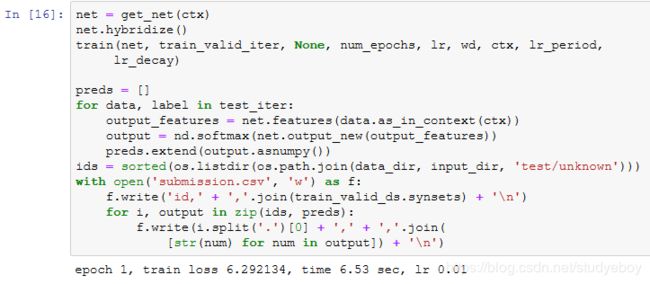
执行完上述代码后,会生成一个submission.csv文件。这个文件符合Kaggle比赛要求的提交格式。提交结果的方法与“实战Kaggle比赛:房价预测”一节中的类似。
小结
- 我们可以使用在ImageNet数据集上预训练的模型抽取特征,并仅训练自定义的小规模输出网络,从而以较小的计算和存储开销对ImageNet的子集数据集做分类。
自然语言处理
词嵌入(word2vec)
为何不采用one-hot向量
![]()
跳字模型
训练跳字模型
连续词袋模型
训练连续词袋模型
小结
- 词向量是用来表示词的向量。把词映射为实数域向量的技术也叫词嵌入。
- word2vec包含跳字模型和连续词袋模型。跳字模型假设基于中心词来生成背景词。连续词袋模型假设基于背景词来生成中心词。
近似训练
负采样
层序softmax
小结
- 负采样通过考虑同时含有正类样本和负类样本的相互独立事件来构造损失函数。其训练中每一步的梯度计算开销与采样的噪声词的个数线性相关。
- 层序softmax使用了二叉树,并根据根结点到叶结点的路径来构造损失函数。其训练中每一步的梯度计算开销与词典大小的对数相关。
word2vec实现
处理数据集
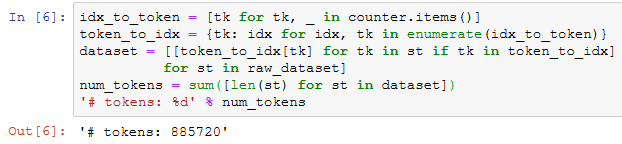
建立词语索引
为了计算简单,我们只保留在数据集中至少出现5次的词。


然后将词映射到整数索引。
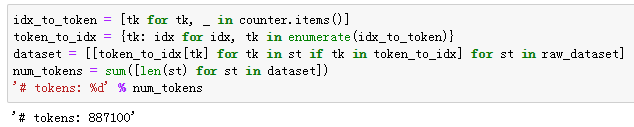
二次采样


![]()
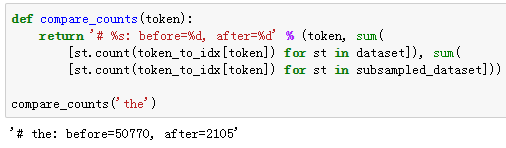
可以看到,二次采样后我们去掉了一半左右的词。下面比较一个词在二次采样前后出现在数据集中的次数。可见高频词“the”的采样率不足1/20。

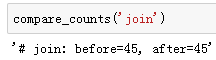
但低频词“join”则完整地保留了下来。

提取中心词和背景词
![]()


![]()
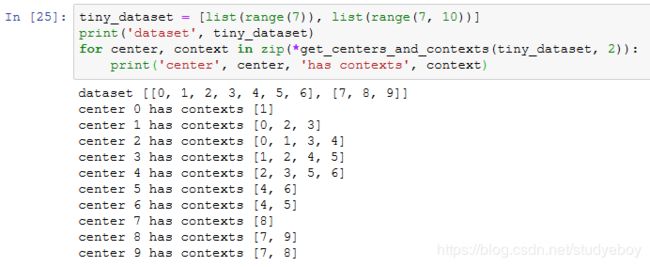
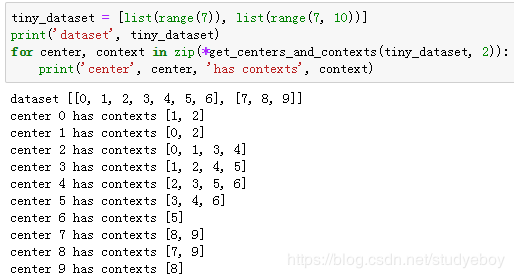
实验中,我们设最大背景窗口大小为5。下面提取数据集中所有的中心词及其背景词。
![]()
负采样
读取数据


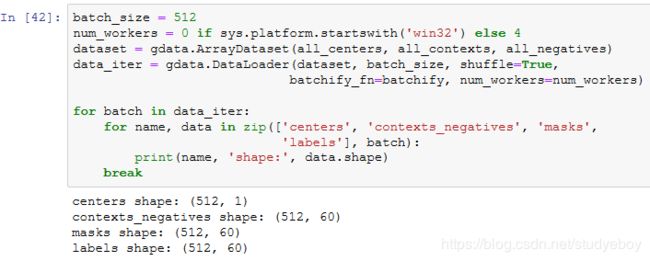
我们用刚刚定义的batchify函数指定DataLoader实例中小批量的读取方式,然后打印读取的第一个批量中各个变量的形状。
跳字模型
我们将通过使用嵌入层和小批量乘法来实现跳字模型。它们也常常用于实现其他自然语言处理的应用。
嵌入层
小批量乘法
跳字模型前向计算
训练模型
在训练词嵌入模型之前,我们需要定义模型的损失函数。
二元交叉熵损失函数
![]()
![]()

![]()
作为比较,下面将从零开始实现二元交叉熵损失函数的计算,并根据掩码变量mask计算掩码为1的预测值和标签的损失。

初始化模型参数
我们分别构造中心词和背景词的嵌入层,并将超参数词向量维度embed_size设置成100。

定义训练函数
下面定义训练函数。由于填充项的存在,与之前的训练函数相比,损失函数的计算稍有不同。
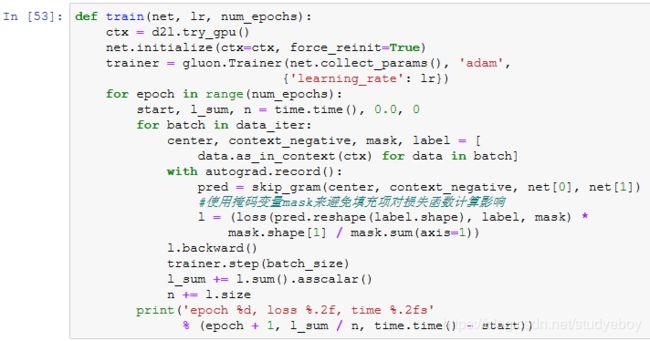
现在我们就可以使用负采样训练跳字模型了。

应用词嵌入模型
小结
- 可以使用Gluon通过负采样训练跳字模型。
- 二次采样试图尽可能减轻高频词对训练词嵌入模型的影响。
- 可以将长度不同的样本填充至长度相同的小批量,并通过掩码变量区分非填充和填充,然后只令非填充参与损失函数的计算。
子词嵌入(fastText)
小结
- fastText提出了子词嵌入方法。它在word2vec中的跳字模型的基础上,将中心词向量表示成单词的子词向量之和。
- 子词嵌入利用构词上的规律,通常可以提升生僻词表示的质量。
全局向量的词嵌入(GloVe)
GLoVe模型
从条件概率比值理解GloVe模型
小结
- 在有些情况下,交叉熵损失函数有劣势。GloVe模型采用了平方损失,并通过词向量拟合预先基于整个数据集计算得到的全局统计信息。
- 任意词的中心词向量和背景词向量在GloVe模型中是等价的。
求近义词和类比词
使用预训练的词向量
![]()

给定词嵌入名称,可以查看该词嵌入提供了哪些预训练的模型。每个模型的词向量维度可能不同,或是在不同数据集上预训练得到的。



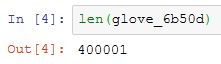
打印词典大小。其中含有40万个词和1个特殊的未知词符号。
我们可以通过词来获取它在词典中的索引,也可以通过索引获取词。

应用预训练的词向量
下面我们以GloVe模型为例,展示预训练词向量的应用
求近义词


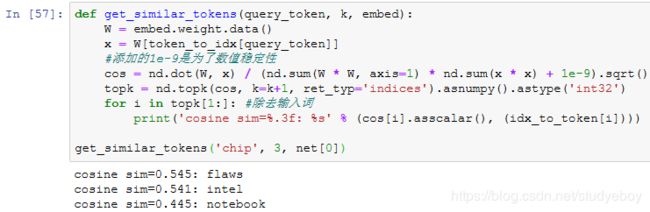
然后,我们通过预训练词向量实例embed来搜索近义词。

已创建的预训练词向量实例glove_6b50d的词典中含40万个词和1个特殊的未知词。除去输入词和未知词,我们从中搜索与“chip”语义最相近的3个词。
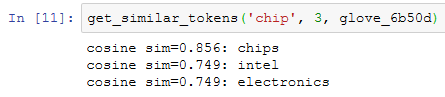
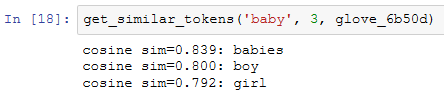
接下来查找“baby”和“beautiful”的近义词。

求类比词


验证一下“男-女”类比。

“首都-国家”类比:“beijing”(北京)之于“china”(中国)相当于“tokyo”(东京)之于什么?答案应该是“japan”(日本)。

“形容词-形容词最高级”类比:“bad”(坏的)之于“worst”(最坏的)相当于“big”(大的)之于什么?答案应该是“biggest”(最大的)。
![]()
“动词一般时-动词过去时”类比:“do”(做)之于“did”(做过)相当于“go”(去)之于什么?答案应该是“went”(去过)。

小结
- 在大规模语料上预训练的词向量常常可以应用于下游自然语言处理任务中。
- 可以应用预训练的词向量求近义词和类比词。
文本情感分类:使用循环神经网络
文本情感分类数据
读取数据
首先下载这个数据集到…/data路径下,然后解压至…/data/aclImdb下。
![]()
接下来,读取训练数据集和测试数据集。每个样本是一条评论及其对应的标签:1表示“正面”,0表示“负面”。

预处理数据
我们需要对每条评论做分词,从而得到分好词的评论。这里定义的get_tokenized_imdb函数使用最简单的方法:基于空格进行分词。

现在,我们可以根据分好词的训练数据集来创建词典了。我们在这里过滤掉了出现次数少于5的词。

因为每条评论长度不一致所以不能直接组合成小批量,我们定义preprocess_imdb函数对每条评论进行分词,并通过词典转换成词索引,然后通过截断或者补0来将每条评论长度固定成500。
![]()
创建数据迭代器
现在,我们创建数据迭代器。每次迭代将返回一个小批量的数据。

打印第一个小批量数据的形状以及训练集中小批量的个数。

使用循环神经网络的模型
加载预训练的词向量
由于情感分类的训练数据集并不是很大,为应对过拟合,我们将直接使用在更大规模语料上预训练的词向量作为每个词的特征向量。这里,我们为词典vocab中的每个词加载100维的GloVe词向量。

然后,我们将用这些词向量作为评论中每个词的特征向量。注意,预训练词向量的维度需要与创建的模型中的嵌入层输出大小embed_size一致。此外,在训练中我们不再更新这些词向量。

训练并评价模型
这时候就可以开始训练模型了。

最后,定义预测函数。

下面使用训练好的模型对两个简单句子的情感进行分类。


小结
- 文本分类把一段不定长的文本序列变换为文本的类别。它属于词嵌入的下游应用。
- 可以应用预训练的词向量和循环神经网络对文本的情感进行分类。
文本感情分类:使用卷积神经网络(textCNN)
一维卷积层
时序最大池化层
读取和预处理IMDb数据集
textCNN模型



创建一个TextCNN实例。它有3个卷积层,它们的核宽分别为3、4和5,输出通道数均为100。

加载预训练的词向量
加载预训练的100维GloVe词向量,并分别初始化嵌入层embedding和constant_embedding,前者参与训练,而后者权重固定。

训练并评价模型
现在就可以训练模型了。

下面,我们使用训练好的模型对两个简单句子的情感进行分类。

![]()
小结
- 可以使用一维卷积来表征时序数据。
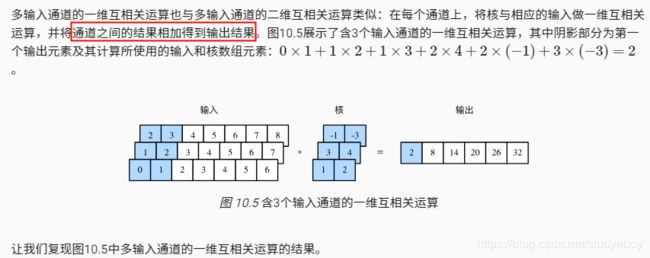
- 多输入通道的一维互相关运算可以看作单输入通道的二维互相关运算。
- 时序最大池化层的输入在各个通道上的时间步数可以不同。
- textCNN主要使用了一维卷积层和时序最大池化层。
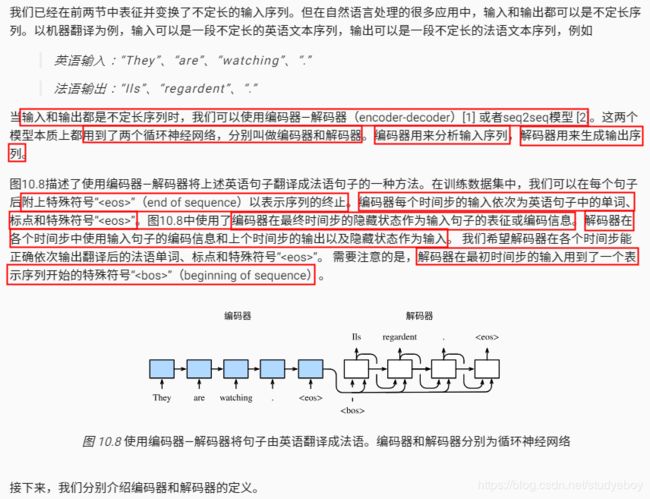
编码器-解码器(seq2seq)
编码器
解码器
训练模型
小结
- 编码器-解码器(seq2seq)可以输入并输出不定长的序列。
- 编码器-解码器使用了两个循环神经网络。
- 在编码器-解码器的训练中,可以采用强制教学。
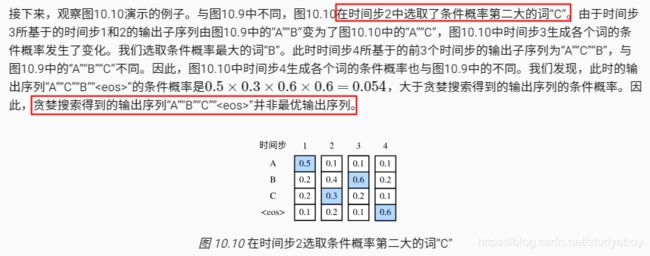
预测不定长序列的方法
贪婪搜索
穷举搜索
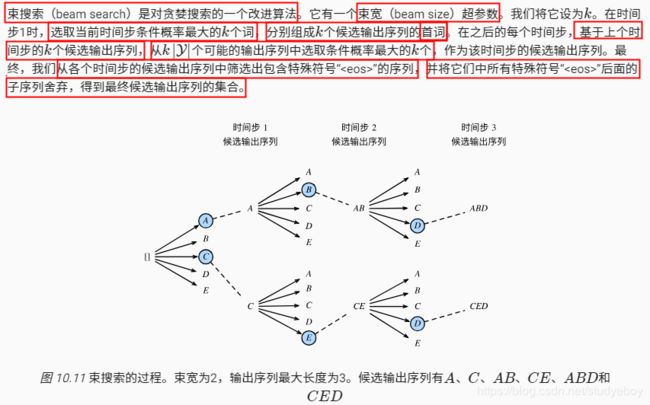
束搜索
小结
- 预测不定长序列的方法包括贪婪搜索、穷举搜索和束搜索。
- 束搜索通过灵活的束宽来权衡计算开销和搜索质量。
注意力机制
计算背景变量
矢量化计算
更新隐藏层状态
发展
小结
- 可以在解码器的每个时间步使用不同的背景变量,并对输入序列中不同时间步编码的信息分配不同的注意力。
- 广义上,注意力机制的输入包括查询项以及一一对应的键项和值项。
- 注意力机制可以采用更为高效的矢量化计算。
机器翻译
机器翻译是指将一段文本从一种语言自动翻译到另一种语言。因为一段文本序列在不同语言中的长度不一定相同,所以我们使用机器翻译为例来介绍编码器—解码器和注意力机制的应用。
读取和预处理数据
含注意力机制的编码器-解码器
编码器
注意力机制
含注意力机制的解码器
训练模型
预测不定长的序列
评价翻译结果
小结
附录
主要符号一览
数学基础
线性代数
微分
梯度向量和Jacobian矩阵
- 梯度向量
目标函数 f f f为单变量,是关于自变量 x = ( x 1 , x 2 , . . . x n ) T x=(x_1,x_2,...x_n)^T x=(x1,x2,...xn)T的函数,单变量函数 f f f对向量 x x x求梯度,结果为一个与向量 x x x同维度的向量,称之为梯度向量。
- Jacobian矩阵
目标函数 f f f为一个函数向量, f = ( f 1 ( x ) , f 2 ( x ) , . . . , f m ( x ) ) T f=(f_1(x),f_2(x),...,f_m(x))^T f=(f1(x),f2(x),...,fm(x))T,其中,自变量 x = ( x 1 , x 2 , . . . x n ) T x=(x_1,x_2,...x_n)^T x=(x1,x2,...xn)T,函数向量 f f f对 x x x求梯度,结果为一个矩阵,行数为 f f f的维度,列数为 x x x的维度,称之为Jacobian矩阵,其中每一行都是由相应函数的梯度向量转置构成的。