12.混淆——混叠图像,对比敏感度,图像压缩_4
目录
混叠图像
对比敏感度
图像压缩
总结
混叠图像
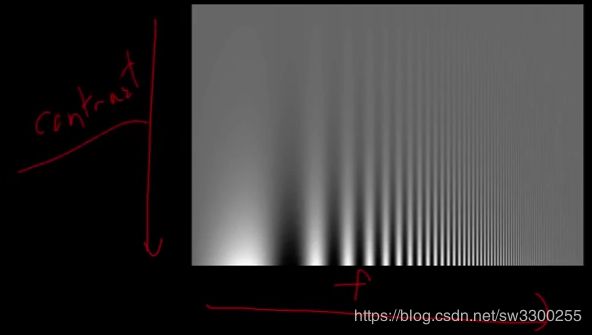
我们可以在图像中看到。这是一张更好的图片显示图像混叠。所以你可以看到,这是一个径向正弦波(Radio sine wave),你可以看到,当你越来越近的时候,像素应该摆动得越来越快(如图)。
最后像素就用完了。Okay,我没有足够的样本来知道变化有多快,这就是混叠的例子(如图)。
那么,它对你有什么影响呢?它对你的影响是你必须谨慎对待你的图像,例如,这来自史蒂夫,all right?假设我有这个图像,一个美丽的梵高图片。 假设它太大而无法放在屏幕上。 我想要一个较小的版本。 我们怎样才能减少它? 我不知道。 使它的尺寸减小一半或四分之一。
嗯,一个明显的方法是扔掉所有其他的列和其他的行,all right?把那些扔掉,这就是所谓的图像子采样(Sub-Sampling)。顺便说一下,这里说的是一半,我的意思是,我扔掉一半的列和一半的行,这当然小了四分之一,right。但一半的意思,一半的行,一半的列。如果我再次这样做,我现在将有四分之一的总行,四分之一的总列,十六分之一的大小。我可以再做一次,八分之一(如图1)。事实上,你可能会注意到这已经有些丑陋了(如图2)。
实际上,为了弄清楚它到底有多丑,让我放大一半,四分之一和八分之一放大两个像素。你会注意到,这很糟糕(如图),okay.
1 / 2看起来不太糟(如图1),但记住这里我们只取了8列中的1列和8行中的1行,然后我们让这个原始图像爆炸。你可以看到这看起来不像原始图像的模糊版本(如图2),原因是我们有混叠。我们不太频繁地进行抽样,因为存在大量的变异。从本质上说,这里的东西摆动的频率比八分之一的要高。所以如果我只取1 / 8,那么,我没有捕捉到所有的摆动。那么,正确的做法是什么呢?
好吧,我们需要做那个抗锯齿(Anti-Aliasing),我们刚刚学会了。 所以,一个简单的就是做高斯,okay? 所以,我们要做的就是过滤,right,所以我们将采用高斯,然后采取其他所有行(如图1),all right? 然后,如果你想对此不那么聪明,你可以做一个高斯,并采取其他每一行,得到四分之一(如图2)。 你可以再次做高斯,并做到这一点(如图3), 或者,你可以做的是你开始做一个更大的高斯,并从每八个中取出一个。 你可以说服自己在数学上这些都是等价的。
当我这样做,并且我将高斯八分之一炸掉时(如图1),你会发现这实际上看起来非常像一个模糊的版本(如图2),对吧? 将此与我们对子采样所做的相比(如图3),right?
所以这是我们的原创(如图1)。这是高斯第八次4倍变焦(如图2)。这里是子样本4倍缩放(如图3),你可以看到高斯函数做的比较好,因为它是抗锯齿(Anti-Aliasing)的。
所以如果你在做电脑视觉,你决定,你知道,我有一个巨大的1920×1080的图像进来,但我只是想识别人脸,好吧,我的脸只有100像素大。你说,你知道吗? 我能做的是,做面部识别是很昂贵的。我们会在整个系列结束时讲到人脸识别。在整个图像上这样做是很昂贵的,因为它太大了。让我画一个图像,八分之一的大小是这样的,八分之一的大小是这样的(手势)。我要把我的脸缩小一点,这样找。你知道吗?如果你做这个,如果你做抗锯齿(Anti-Aliasing),那就会很好。如果你把任意像素都拉出来,就会把整件事弄得一团糟。你会得到混叠,然后脸就不好看了。这就是为什么在计算机视觉中做这些事情很重要。
对比敏感度
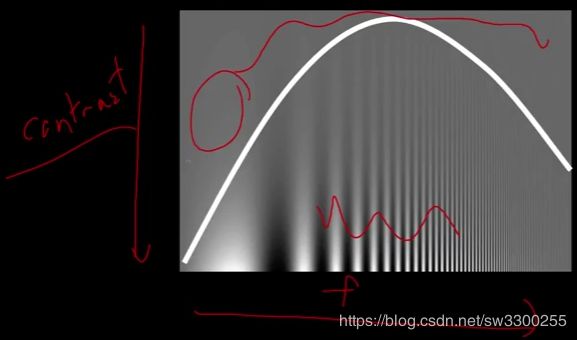
这几乎结束了我们关于频率的课程。还有一件事我今天想和你们谈谈,因为它在你们将要做的处理过程中非常普遍。一些心理学家,坎贝尔和罗布森很久以前研究过人眼的对比敏感度,人类的视觉系统不仅仅是眼睛。现在你看到的是一个频率上升到右边,对比度下降的曲线(如图)。
也许,如果你像我一样,希望你不要像我一样,我中的一个已经足够了,我的孩子们会告诉我的。
但不管怎样,如果你像大多数人一样,你可能会很好地看到这些东西(如图1),但在这上面没有那么多(如图2)。
在那里的某个地方,那条曲线就是坠落的地方(如图),
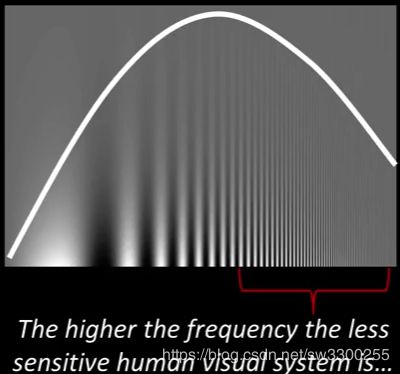
本质上,你知道,这里的对比度比较低(如图1),你看不到变化。高对比度也一样(如图2),okay?你的眼睛在不同方面都很敏感。所以这意味着一些频率在图像中对你的重要性更大,okay。特别是,如果我把一组FRQ,FRQ是频率(如图3)。也就是说,如果在高频处有低对比度(如图4),你甚至不知道,所以你可以用它来做图像压缩(Image Compression)。
图像压缩
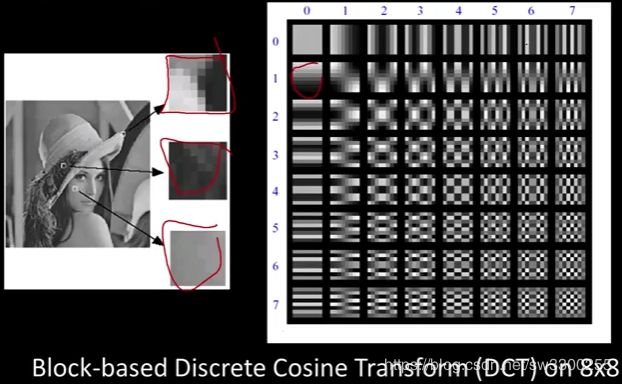
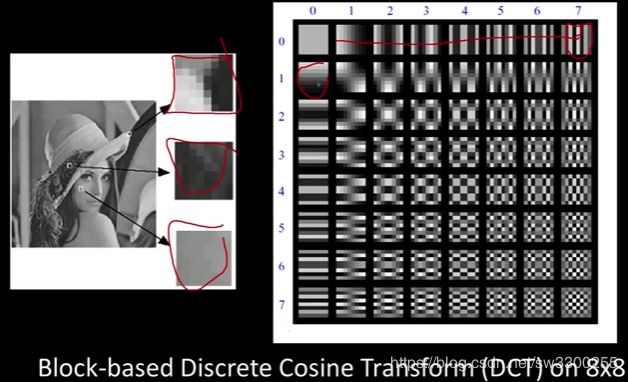
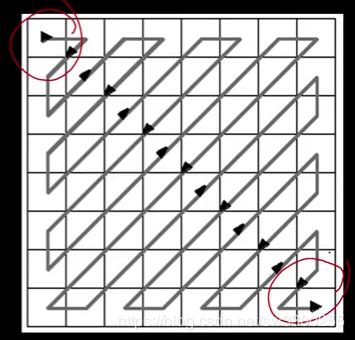
你可能听说过JPEG,可能在你周围都有JPEG图像,okay。JPEG使用所谓的离散余弦变换,或者其中的变换。一种基本的思考方式是取图像的8x8区域,把整个区域分割成8x8的小块(如图)。
然后它把这些正弦(sinusoids)(如图1)和 协正弦(co-sinusoids)(如图2)作为基集。这里我们有垂直的(如图3),这里有下来的(如图4),这里是它们的乘积(如图5)。
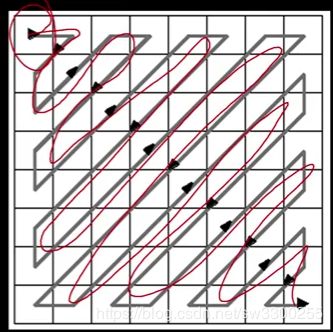
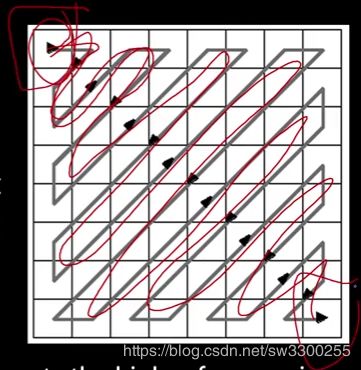
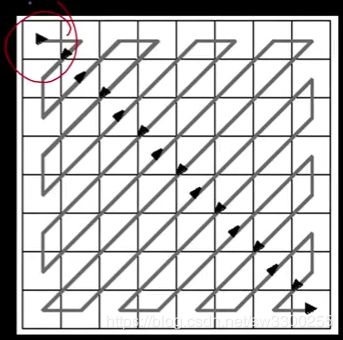
你可以看到低频在左上角,高频在右下角(如图1)。所以你能做的是,你可以说,这些中有多少是我需要画出来的? 实际上你可以对它们进行排序。你可以这样排列它们(如图2)。这个想法是,左上角可能是(如图3),事实上回到这里(如图4)。你知道这是常数吗?(如图5)okay,那就是,如果你,这只是图片的平均值。所以左上角,有时称为B(0,0),就是直流分量,平均值,然后随着你越来越远,频率越来越高(如图6),所以左上角代表较低的频率,右下角代表更高的频率(如图7)。
我们之前说过,我们不需要表示更高的频率,right? 只是一些高对比度的成分。 这样做的一个方法是,如果我们把这些系数(如图1)编码得更好,比这些系数(如图2)多一些?
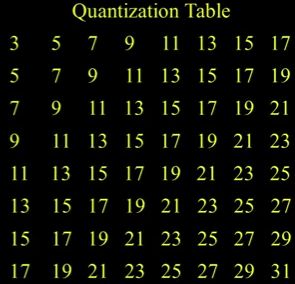
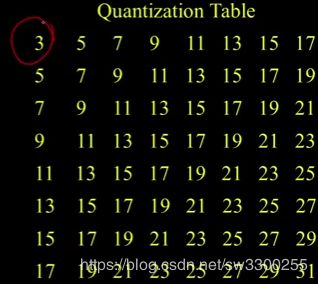
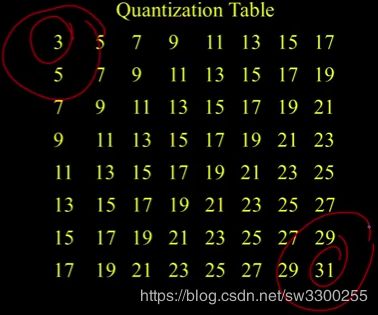
这就是所谓的量化表(如图1),DCT(离散余弦变换-Discrete Cosine Transform)做压缩,所以这3的意思是(如图2),我们保持系数为最近的三个值,所以如果你用比特来考虑这个,你可以把它平移2个单位,它的思想是把这个四舍五入到最近的3,okay。
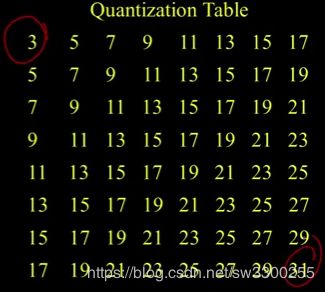
而这个四舍五入到最近的31(如图1)。换句话说,左上角的表示法比右下角的表示法要多(如图2),okay,所以这意味着你失去了信息,但你在这里失去了很多信息(如图3),okay。
顺便说一下,在给定频谱的情况下,您可以进行逆傅立叶变换,您可以重建信号。DCT也是如此。IDCT,逆DCT(inverse DCT)。给定这些系数,我可以重建图像。但是现在,我不会精确地保持所有这些系数,我只会保留更多关于低频系数的信息而不是高频系数的信息。这对于人类的视觉系统非常有效。
如果你看一下你的普通JPEG图片,这里有一个我从网上偷来的例子,所以他们用89000字节的信息来表示这张图片,只使用原始强度和为12000字节的图片,两者是是7比1的比例,使用DCT系数,JPEG标准,all right。它之所以能起作用,总而言之,是因为图像的频率是不同的,这是我们的基集。人类的视觉系统对不同频率、不同数量的图像是敏感的。通过做类似于傅里叶变换的运算你得到这个积分或者这个和,这个点积和摆动的正弦信号,DCT是它的一个变体,我们可以算出每个频率的系数。然后,为了在描述图像时节省大量的字节,可以实质上阈值化或降低高频的表示水平。
总结
好了,这就结束了我们在频率上的系列。我敢打赌你很高兴,因为这一切结束了。正如我刚才所说的,如果你作为一名电气工程师进行图像处理,你将会做大量的工作,根据图像的频率内容分析图像。你会考虑图像处理操作的频率特性。然而,我们只会做一点点,因为作为计算机科学家,我们倾向于把图像看成是数据结构,而不是信号。但是,当我们尝试做像光流这样的事情时,我们仍然需要担心像频率内容这样的事情,在这些事情中,我必须使图像在近似的距离上变化不大。所以实际上你必须做一个过滤,去除那种高频率。所以,希望你现在对傅立叶的分析和频率有足够的了解是危险的。我们将继续练习在即将到来的演讲中练习危险。
——学会编写自己的代码,才能练出真功夫。