“抽象”《大话数据结构》第七章——图(至存储结构)
图的定义
基本定义
图是由 顶点的有穷非空集合 和 顶点之间边的集合 组成。通常表示为:G(V,E),其中G代表一个图,V代表顶点,E代表边缘。
顶点的有穷限制了边的有穷性,但是在顶点非空的情况下,边可以是空集。
| 无向图 | 有向图 |
|---|---|
| 由无向边构成,无向边用无序偶对(Vi , Vj)表示 | 由有向边构成,有向边用有序偶对 |
| 无向边没有方向 | 有向边有方向,由弧尾指向弧头 |
| – | – |
| 无向完全图 | 有向完全图 |
| 任意两个顶点之间都存在边 | 任意两个顶点之间都存在方向相反的两条弧 |
接下来是有向图和无向图共有的称呼:
| 稀疏图 | 稠密图 |
|---|---|
| 边或者弧相对较少 | 边或者弧相对较多 |
有些图的边或弧具有与它相关的数字,这种与图的边或弧相关的数叫做权。这种带权的图通常叫做网。
假设有两个图G = (V,{E})和G’ = (V’,{E’}),如果V’包含于V且E’包含于E,则称G’为G的子图。
若不存在顶点到其自身的边,且同一条边不重复出现,则称这样的图为简单图。
其它概念定义
邻接点:两个顶点之间存在边,这两个顶点就互为邻接点。在有向图里面成为相关联。
依附:两个顶点之间存在边,这条边依附于这两个顶点。
度:某一个顶点有多少条边跟它有依附关系,度就边的数目。在有向图里面还分出度和入度。
环:路径最终回到起始点
简单路径:除了起始点和
连通图:任意两点都是连通的,而不是任意两点间都有边或者弧
强连通图:针对有向图,对任意一对顶点,都存在路径。
连通分量:无向图的极大连通子图
强连通分量:有向图的极大强连通子图
生成树:对于n个顶点的图
- 若边数 < n-1,能构成生成树
- 若边数 > n-1,必构成环
- 若边数 = n-1,不一定
有向树:如果一个有向图恰有一个顶点的入度为0,其余顶点的入度均 为1
图的抽象数据类型
数据部分:
- 顶点的有穷非空集合
- 边的集合
操作部分
1.增加结点,删除结点
2.深度优先遍历,广度优先遍历
3. 创建图
4. 增加弧,删除弧
图的存储结构
邻接矩阵
存储思路
邻接矩阵存储方式是用两个数组来表示图。一个一维数组存储图中顶点信息,一个二维数组存储图中的边或者弧,这个二维数组就称为邻接矩阵。
 这是无向图的邻接矩阵,由于无向图里面(V1,V2)= (V2,V1),所以该邻接矩阵就成为了对称矩阵。
这是无向图的邻接矩阵,由于无向图里面(V1,V2)= (V2,V1),所以该邻接矩阵就成为了对称矩阵。
- 某个顶点的度其实就是该顶点所在的行或者列的元素加起来。
- 某个顶点的邻接点,其实就是该顶点所在的行或者列不为零元素的另一个维。
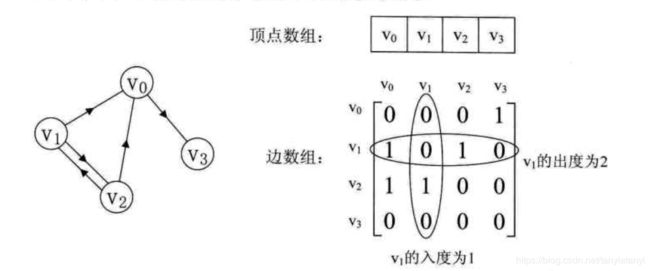
这是有向图的邻接矩阵,由于有向图的每一条弧都是有向的,所以可以约定二维数组的行标代表弧尾,列的序号代表弧头。
1.某一顶点的出度为该顶点所在的行不为0的元素之和
2 .某一顶点的入度为该顶点的列不为0的元素之和
无向图和有向图都存在每条边或者弧带有权值的情况,术语叫做网。
约定:
typedef char VertexType;
typedef int EdgeType;
#define maxvex 100
#define INFINITY 65536
typedef struct
{
VertexType vexs[maxvex];
EdgeType edges[maxvex][maxvex];
int numvertexes,numedges;
}GRPH;
创建一个无向网图:
1 获取网图的顶点数和边的数目
2 通过循环写入顶点信息
3 初始化邻接矩阵
4 通过循环建立邻接矩阵
代码如下:
void CreateGraph(GRPH G)
{
int i,j,k,weight;
printf("please input the number of vex and edge");
scanf("%d, %d",&G->numvertexes,&G->numedges);
printf("Please input vex");
for(i = 0; i < G->numvertexes; i++)
scanf(&G->vexs[i]);
for(i = 0; i < G->numvertexes; i++)
for(j = 0; j < G->numvertexes; j++)
G->edges[i][j] = INFINITY;
for(k = 0; k < G->numvertexes; k++)
{
printf("please input (Vi,Vj) and weight")
scanf("%d %d %d",&i,&j,&weight);
G->edges[i][j] = weight;
G->edges[j][i] = G->edges[i][j];
}
}
邻接表
邻接表是针对顶点多,边数少时,邻接矩阵造成的存储空间浪费改进的,它是数组和链表相结合的存储方法。
无向图:

顶点存储在数组中,数组中指针域指向该顶点的邻接表的第一个结点。
1 求某一顶点的度,就去遍历它的邻接表
2 求某一顶点是否和另一顶点之间是否有边,还是需要遍历某一顶点的邻接表,看是否有另一顶点的下标
3 若求某一定点的所有邻接点,则需要遍历该顶点的邻接表
有向图:

以顶点为弧尾来存储邻接表的方式,可以很容易的到某一个顶点的出度。同理,若以顶点为弧头来存储邻接表,则通过遍历邻接表,可以很容易的到该顶点的入度。
网图:

这是有向图的网图。
数据结构:
1 边表结点 = 邻接点域 + 权值 + 指针域
2 顶点表结点 = 顶点数据域 + 边表指针
3 操作结点 = 顶点表的指针 + 顶点数和边数
代码如下:
typedef struct EdgeNode
{
int adjvex;
int weight;
struct EdgeNode *next;
}EdgeNode;
typedef struct VerterNode
{
VertexType data;
EdgeNode *firstedge;
}VerterNode,Verter[maxvex];
typedef struct
{
Verter *verter;
int numvertexes,numedges;
}GraphVerter;
创建邻接表
1 通过输入获取图的顶点数和边的数目
2 通过循环输入顶点的数据,同时指针域为NULL
3 通过循环分别在两个相关顶点的邻接表采用头插法插入新的结点
代码如下:
void CreatALGraph(GraphVerter *G)
{
EdgeNode *e;
int i,j,k,weight;
printf("Please input number of VEX and EGDE");
scanf("%d %d",&G->numvertexes,&G->numedges);
for(i = 0; i < G->numvertexes; i++)
{
scanf(&G->verter[i]->data);
G->verter[i]->firstedge = NULL;
}
for(k = 0; k < G->numedges; k++)
{
printf("Please input Vi, Vj and weight")
scanf("%d %d %d",&i,&j,&weight);
e = (EdgeNode*)malloc(sizeof(EdgeNode));
e->weight = weight;
e->adjvex = j;
e->next = G->verter[i]->firstedge;
G->verter[i]->firstedge = e;
e = (EdgeNode*)malloc(sizeof(EdgeNode));
e->weight = weight;
e->adjvex = i;
e->next = G->verter[j]->firstedge;
G->verter[j]->firstedge = e;
}
}
十字链表
为了解决同时能够比较方便知道某一顶点的出度和入度,重新定义顶点结点和边表结点。(针对有向图或者网)

顶点结点分别拥有数据域,出度指针域,入度指针域,指针分别指向入度边表和出度边表的第一个结点。

数据域:
tailvex是指弧的起点在顶点表中的序号
headvex是指弧的终点在顶点表中的序号
指针域:
headlink指向终点相同的下一条边
taillink指向起点相同的下一条边

邻接多重表
解决有时候更多的是对边进行操作带来的不便**(针对无向图)**
重新定义边表结点:

指针域:
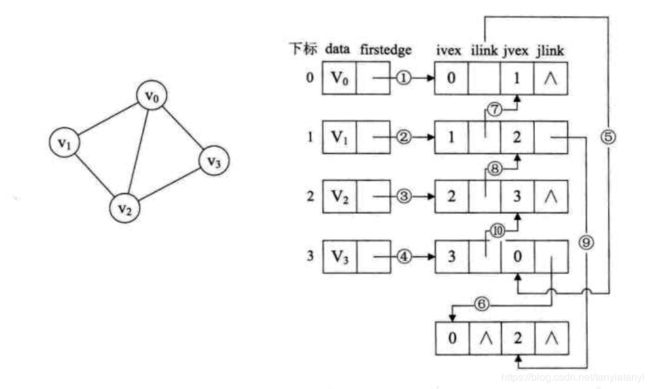
ilink指向依附于顶点ivex的下一条边
jlink指向依附于顶点jvex的下一条边
数据域:
ivex和jvex是成对出现的,是某一条边依附的两个顶点
边集数组
由两个以为数组组成,一个存储顶点信息,一个存储边表信息。存储边表信息的数组的每个元素包含每条变得起始顶点和结束顶点,还有权值。

