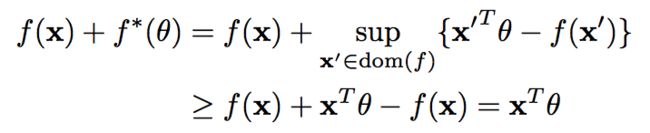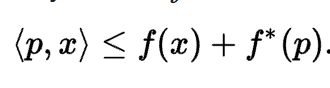首先听闻唯一的女性菲尔兹奖得主,玛利亚姆·米尔扎哈尼Maryam Mirzakhani, 去世了,有点伤心。 因为一般数学家, 除了意外, 都还活的比较久。 据说压力太大, 罹患癌症。 但愿大家不要长期处于大鸭梨下生活。玛丽亚姆, 脱下头巾, 站上讲台, 绘出那美丽眼睛看到的神奇世界, BLESS!
然后, 这里回到最优化的武侠世界,我们开始走进天下五绝之首,中神通Fenchel。 我们在"一挑三 FJ vs KKT"给出最优化之东西西毒,南帝北丐,中神通 (见附录)。
前言
Fenchel出生在德国柏林的犹太家庭, 博士毕业于柏林大学。
这个德国出生的年轻人的第一份工作就在哥廷根数学研究所(the Mathematical Institute in Gottingen),跟从Edmund Landau做凸优化相关研究, 注意这个Landau不是物理界的神Lev Landau。
首先哥廷根数学研究所不是一个简单的地方,高斯,黎曼,希尔伯特,克莱因,卡拉西奥多里,狄利克莱,冯诺依曼都在这里工作过。
其次, 他的博士导师Ludwig Bieberbach就是研究不等式的大师, 而Ludwig的导师就是克莱因, 所以他是克莱因的徒孙。 Ludwig把自己优秀的学生Fenchel介绍给自己在Gottingen的好友Edmund做助理。
从此, Fenchel利用继承Ludwig搞不等式的精神来做Edmund的凸优化,这个世界上最优秀的凸优化大师的课题。 一下子奠定了凸优化的基础,开启了凸优化发展的新模式-对偶模式。
由于纳粹的影响, Fenchel被迫离开了心爱的哥根廷,去了丹麦的哥本哈根 。凡事好坏皆有, 好事是, 在那里他和犹太女数学家Käte Sperling结婚了。 Kate是非阿贝尔群方面的大师。 两人数学伉俪在哥本哈根也被占领后被迫去了美国, 但是战后, 又回到了哥本哈根大学, 并在那里生活了一辈子。
另外,随便提一下。Fenchel有个微分几何数学家好朋友,叫Busemann。就是下面图片,浅色西装那位,他会的工作语言有French, German, Spanish, Italian, Russian, 和 Danish。口语还有Arabic, Latin, Greek and Swedish。 简直太牛了! 我们知道Boltzmann、Lagrange和Kolmogorov等大数学家,最早也是学习语言和历史,然后转到数学的。所以如果想要学好数学, 请先学好语言学。
下图: Werner Fenchel, Alexander Danilowitsch Alexandroff, Herbert Busemann, Børge Jessen 的合影。
从Legendre变换到Fenchel共轭
Fenchel共轭的研究,是对Legendre变换的一个扩展(参考 "Legendre变变变" ), 突破了Legendre对凸可导的限制。
对于不可以求导的, 没有导数。
另外一种情况下, 就是对于非凸的情况,导数不唯一。
那么, Fenchel是怎么解决这个问题的呢? 一方面要兼容Legendre的导数支撑面, 另外一方面要让不可导或者非凸情况下, 具有函数的唯一性。
Fenchel利用了罗尔定理到中值定理中描述的极值和导数的关系。用极大或者极小值来隐含导数的关系。
另外极值, 在非凸情况下的线性外包络是凸函数。
这样使得Fenchel共轭函数的性质非常好。 当然Legendre肯定不是故意忽视这个方面的, 而是在当时物理的发展应用下, 没有这个需求。
Fenchel共轭的三个视角
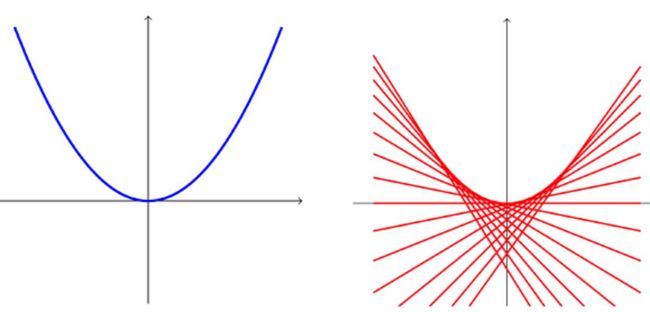
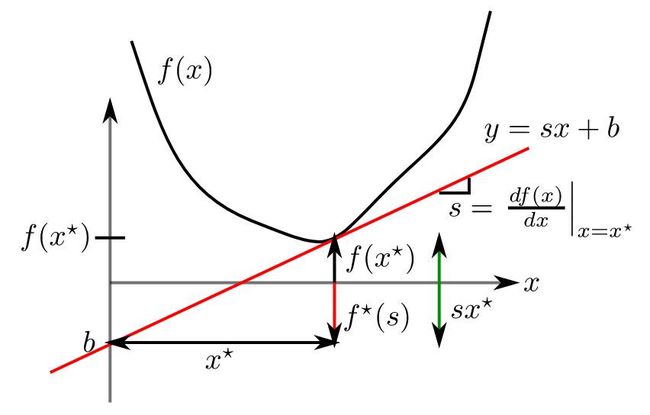
一:切线支持面
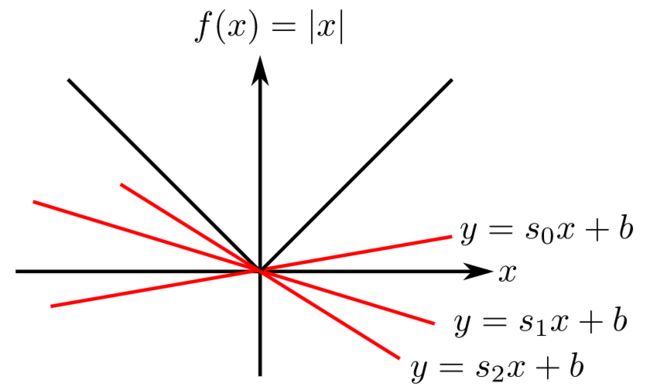
在这种理解下, 我们细看一下,Fenchel共轭函数,它是切线簇的截距b的负值簇。
假设斜率s,那么固定s情况下, 经过一个切点( x*, f(x*) )的直线的截距和x*围成一个直角三角形。 这个直角三角形的斜率s为垂直边长度比上水平边长度的比值。 或者说水平边长度乘以斜率得到垂直边长度。
这样我们找到了截距和斜率直接的关系, 在这个关系里面, 稍微有点不和谐的是负的斜率。 但是这样写成斜率的一阶形式,比较好看些。 那剩下来的问题, 只要确定这个切点就可以了。
在这一层理解上, 你会发现一个很有意思的东西,就是一个函数和它的Fenchel共轭之间通过切线联系起来。 更好玩的是,如果继续对共轭再取共轭,又回到了原函数。 所以,开启了凸可到函数和切线之间的神奇模式。
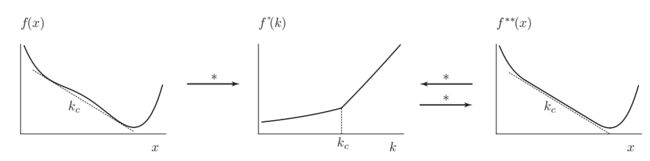
二: 曲线上到过原点斜线最远距离
对于非凸的情况,切线支撑面可能就不太好理解了。 但是这个毕竟是最早的思想的来源。 如果换成极值的情况下。 就是先固定一个斜率, 然后作过原点的直线, 然后找直线上所有的点里面到这个点垂直距离最大的点, 当然这里要考虑正负号的计算。
用固定斜率直线上的点, 减去曲线上的点。 当然, 如果你从最远点做一条平行线, 可以证明这个线在凸可导的情况下是切线的。所以,这样可以从图形上理解, 从Legendre变换到Fenchel共轭的演变。 就是把切线平移到过原点, 把截距变成了斜线上点到切点的垂直距离。
这是理解Fenchel共轭的第二层境界, 有了这层境界,就可以理解Bregmen Divergence距离的用意了。Bregman散度的定义如下:
Bregmen散度的几何意义非常清楚, 就是下图,红色线的长度。 但是为什么要计算这个距离呢?假如你不知道Bregman散度,但是知道KL散度,那么KL散度,可以看成是Bregmen散度的一个特例, 是不是一下子就重要了?
我们看一个东西, Fenchel共轭的共轭:
从上面,可以看到很明显的有如下公式
而Bregman距离,就是告诉你在Fenchel共轭里面, 这个单一线情况的距离。 尤其对于部分非凸的情况下的闭包设计。 这样,大家也可以去理解一下,共轭的共轭的对于非凸函数的伟大意义了。
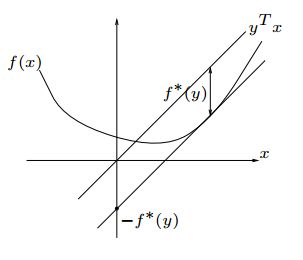
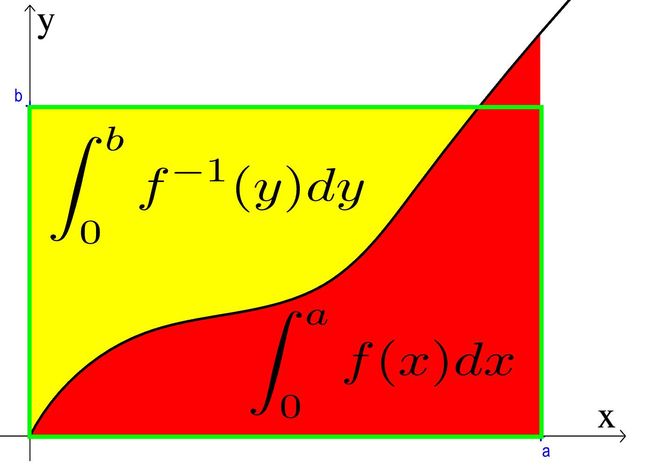
三:曲线的垂直轴的积分
接下来, 我们要讲Fenchel共轭理解的第三层境界。 理解了这一层境界,就可以对Fenchel函数的各种高深性质进行直观理解了。
如果我们直接把切线看成一个函数,把凸函数本身看成是一个积分, 那么一个函数和它的共轭就是同一个导数曲线分别对X轴和Y轴的积分, 所以他们相加起来, 结果为正方形的大小XY。 根据逆函数的性质, 所以我们知道共轭函数的导数互为逆函数。 这就是在第一层境界里面理解的神奇的本质关系。
那么, 按这个理解, 对于其他情况呢?其实也是类似的, 只是不是XY,而是差了一个曲线围住的常数。 这里就不展开了。
Fenchel-Young 不等式
直观上理解Fenchel不等式
Fenchel不等式证明非常容易。
但是如何联系图形图像去理解, 一旦有了第三层对Fenchel共轭的理解之后就很容易从图形上去理解Fenchel不等式了。
如下图所示, 当给定的矩阵,不是刚好落在导数上的时候, 那么矩阵的面积就小于两个积分之和了。
其实这个积分性质最早是William Henry Young发现的。 不过Fenchel在凸优化里面应用的出神入化!
Fenchel 不等式的巨大能力
Fenchel不等式的强大在于对一些对偶问题建立了统一的理论解释。
譬如, 学过SVM的朋友肯定知道Lagrange Duality 对偶方法。而且根据对偶的解释也知道了KKT条件(参考一挑三 FJ vs KKT)。
之前, 我们理解Lagrange对偶的方法, 都是通过冯诺依曼的最小最大定理(von Neumann-Fan Minimax Theorem)来说明的:
但是没有解释Lagrange表达式是如何来的。 也没有几何上的很好的解释。但是, 通过Fenchel不等式就可以直观的解释这些。那么, 神奇的Lagrange表达式是如何来的呢?
从上面, 我们清楚的看到了Lagrange表达式是Fenchel对偶的演绎。既然是Fenchel对偶, 那么就有Fenchel不等式成立。
再回到,Fenchel不等式理解什么时候等式成立的条件, 又回到了Legendre变换和Fenchel共轭的的差异。 再回过来体会, Lagrange对偶的成立条件。 是不是一下子就联系起来了?
Fenchel对偶
基于扰动函数的对偶
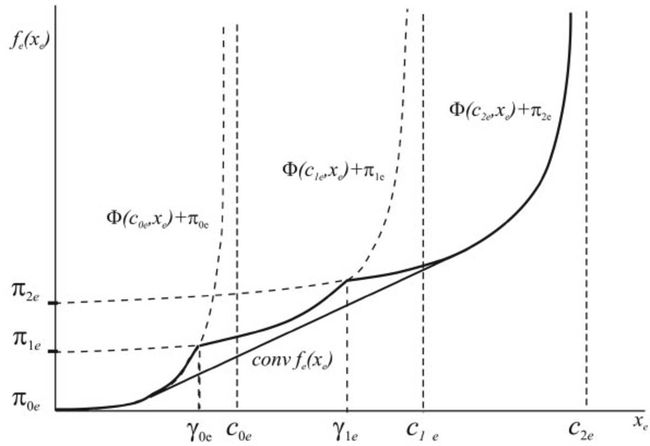
有了上面对Fenchel共轭的理解, 那么我们就可以知道共轭的共轭,是对原来函数的一个凸闭包。 当然, 如果原来函数已经是凸函数了, 那么共轭的共轭就是自己了。
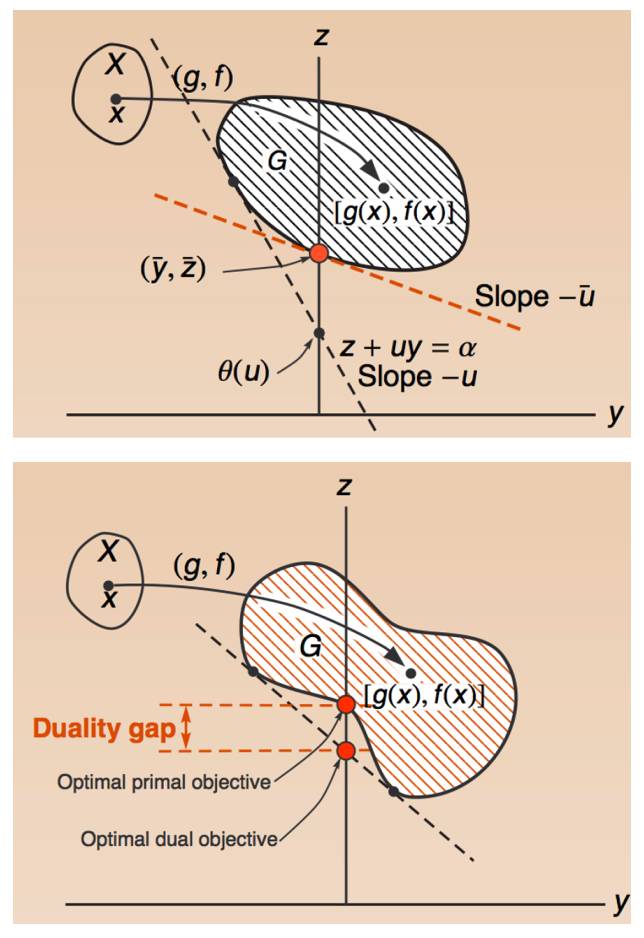
如果我们把前面提到的Perturbation函数拿出来分析, 而不去考虑后面具体的公式。 我们可以看到强对偶和弱对偶的情况下的不一致。
假如我们直接基于Perturbation扰动函数,利用Fenchel共轭的关系开始建立对偶关系。 详细的推理过程就省略了, 大家有兴趣可以自己根据前面类似的过程, 利用Fenchel不等式, 推理一下。
注意这里0点的选择,这也是为什么你看到的所有的对偶的图示里面, 基本围绕扰动函数0点的值。
Fenchel对偶
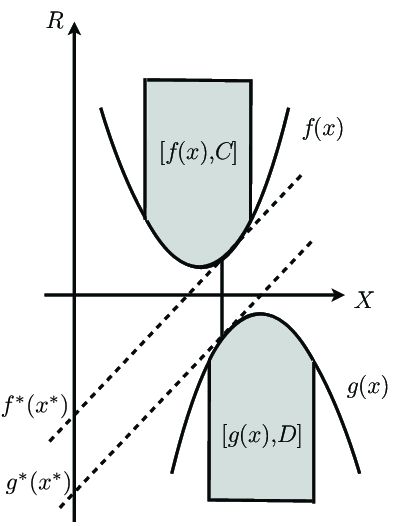
Fenchel对偶,可以看成是Lagrange对偶的一种应用。
当然,你也可以表示成两个函数的和的形式。 只是, 第二个函数在图示上,就变成了-f2(x)了。
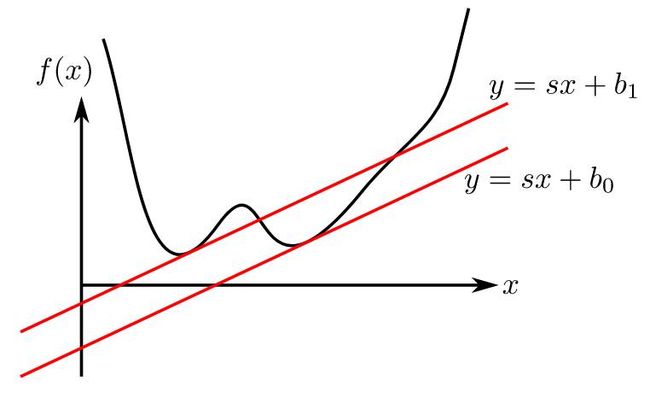
可以看到,Fenchel对偶的含义就是找到, 截距值差最大的那组平行切线。
小结:
我们这里介绍了凸优化和对偶的中神通Fenchel, 有了Fenchel,有了FJ,KKT(参考一挑三 FJ vs KKT)等等就有了很强大的凸优化的工具集合了。
最后,这种扰动函数加切线闭包的思想,进一步衍生, 可以把切线修改成切二次曲线, 然后就会得到更为神奇的结论, 是什么呢? 希望以后有时间具体描述。
这一系列对优化继续深入的公众号文章,希望能够帮到您学习最深的人工智能和机器学习。的确个人时间不够,难以深入太多!
附录:
最优化之 东邪西毒 南帝北丐
东邪 Dimitri Bertsekas MIT
西毒 Stephen P. Boyd Stanford University
南帝 Andrzej Ruszczyński Rutgers University
北丐 Stephen J. Wright, University of Wisconsin
郭靖 Mark Schmidt, University of British Columbia
中神通 Werner Fenchel
中顽童 Jean Jacques Moreau
相关话题:
概率分布の三奥义
变分の美
矩阵分解 (乘法篇)
矩阵分解 (加法篇)
矩有四子
最大似然估计的2种论证
信息熵的由来
“66天写的逻辑回归” 引
一步一步走向锥规划 - LS
一挑三 FJ vs KKT
收敛率概述 (Overview of Rates of Convergence)
迭代优化算法之直观概述 (SVRG)
参考:
http://aapt.scitation.org/doi/pdf/10.1119/1.4795320
http://odessa.phy.sdsmt.edu/~andre/PHYS743/lfth2.pdf
https://mli7.wordpress.com/2011/04/
https://opc.mfo.de/detail?photo_id=1094