深度学习 第一章 深度学习简介

深度学习入门-唐宇迪 （笔记加自我整理）

深度学习 第一章 简介

1.安装anaconda

     Anaconda是最方便的环境，其他的库都可以安装，建议使用anaconda自带的安装命令。初学者不建议再环境上浪费太多时间，容易打消积极性，anaconda集成环境非常棒。

2.常规套路

    和考试的套路一样，要先收集之前的测试题，要知道这些题的正确答案是什么；然后开始做题训练，大概率会有个知识体系，知道什么样的题答案是什么；然后需要通过一些模拟考试测试评估，评估下自己学习的程度，比如满分100分自己可以得到多少分。

• 收集数据，给定标签
• 训练一个分类器
• 测试、评估

3.超参数选择

      参数一般是可以学习到的，比如用线性回归模型，每个特征的重要性是多少，也就是权重，都是可以学习到的；而超参数一般都是指定的，比如说k近邻算法，判断一个样本属于哪一类，是和这个样本周围最近的样本相关的，k就是超参数，比如指定为3，那么就是最近3个样本属于哪一类，如果指定为5，就是最近的5个样本属于哪一类。

     不管是机器学习还是深度学习，一般用于训练模型的数据，和用于评测的数据，是完全不重复的，就好像要准备考试，考试题不会是联系题原题。但是训练集中也会存在问题，比如收集到的题覆盖度是不是够，会不会这次的题比较简单，下一波题比较难，两波题的难度不一样怎么综合衡量能力。

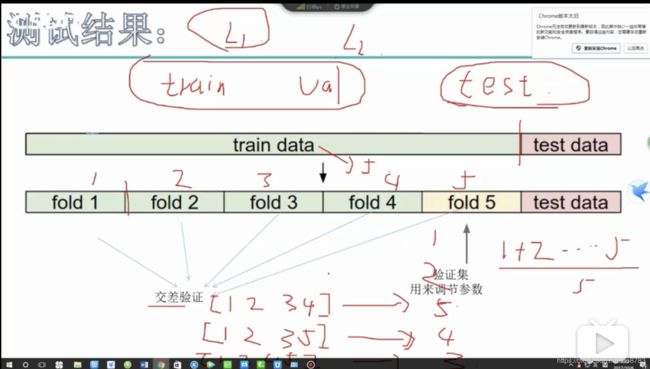
     这里很常见也很关键的方法，就是交叉验证，就是把训练集分成多份，一般会选择5、10份，分成其他份也可以，然后把一份留出来作为测试集，就是考卷，其他几份数据当做训练集，放到模型里建模学习；对于每一份测试集都采用同样的操作，把每一份测试集的评测结果取平均值，就是最终的效果，这样的好处是，不管简单的题还是难的题都学习到了，而且取得的平均值，更能衡量学习能力。

• 交叉验证：平均值作为验证集总效果
  • k-fold，将训练集切分成k份，这里是5
  • 每一份作为验证集，其他四份作为训练集训练
    • 【1，2，3，4】->建模， 5作为验证集
    • 【1，2，3，5】->建模， 4作为验证集
    • 【1，2，4，5】->建模， 3作为验证集
    • 【1，3，4，5】->建模， 2作为验证集
    • 【2，3，4，5】->建模， 1作为验证集
  • 验证集效果：1+2+3+4+5/5 (5份验证集结果取平均）

            

 

4.得分函数

     得分函数，可以理解为最终要使用的规则，也就是最终产出的模型，模型用函数的方式表示。以线性模型为例，有不同维度的数据输入，比如身高、体重、年龄、收入、花销等等，来预测这个人消费水平大概是多少，通过一些数据去建模学习，最终想要知道每个维度对应的重要性，比如身高的重要性是多少，收入这个维度的重要性是多少，这里每个维度对应的重要性就是权重，就是每个维度数值*该维度的重要性，得到的结果值就是这个人的消费水平，而这个过程就是得分函数。

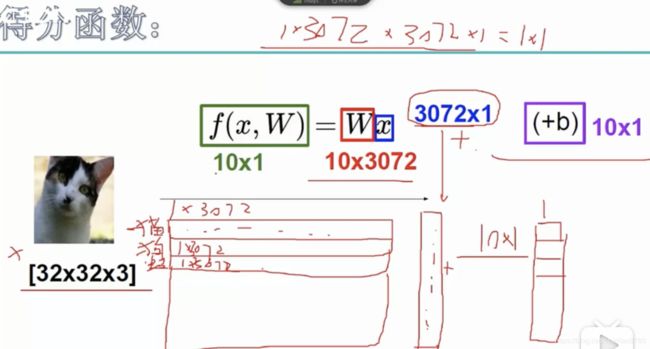
    下面的例子是图像识别的例子，输入的是图片的像素，图片在人脑里面就是一张图片，在计算机中是采用像素来存储的，可以简单理解为存储方式不一样，反正内容还是看到的图片。假设输入一张图片，图片维度是3072，图片上每个维度的重要性是不一样的，图片像素乘上对应的权重，一般还要加上一个常量值，最后输出是每个类别的概率值，比如这个得分函数有10个类别，每个类别对应一组权重和偏置项，每个类别会一个得分值，最终哪个类别的得分值高，比如预测为猫的概率值最大，那么就判断为该图片是猫。这就是得分函数计算的过程。

    一般用W表示权重，大写表示是矩阵，b表示偏置项或者是常量，有了b梯度下降的时候才会收敛。

• 函数定义：
  • f（x，w） = W * x + b 
    • W表示权重参数，b表偏置项

                              

• 计算过程： 
  • W = 3*4 ，3表示预测类别，4表示每个类别向量的维度 
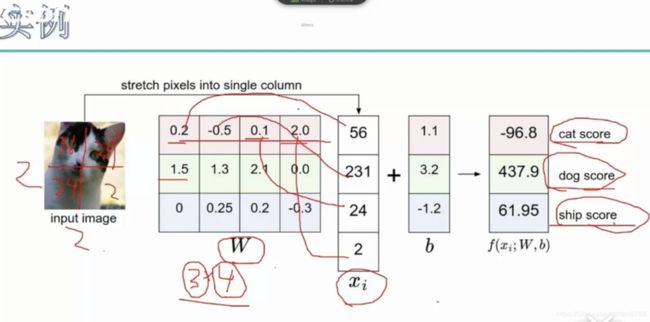
  • Cat score : 0.2*56+-0.5*231+0.1*24+2.0*2 + 1.1 = -96.8
  •  dog socre：1.5*56+ 1.3*231+ 2.1*24+0*2 + 3.2 = 437.9
  •  ship score:  0* 56 + 0.25* 231+0.2*24+-0.3*2+ -1.2 = 41.95

     这里可以简单理解为，一张图片xi一共有四个输入，W表示每个维度输入的重要性，假如对于猫来说，第一个为维度重要，对于狗来说，第二个维度重要，就是用W来表示的，这里假设我们要判断的是3分类，就是最后从猫，狗，青蛙三者选一种，具体计算过程如上图所示，最终狗类别的得分比较高，模型会判断该图片是狗（人眼看图片是猫，说明这个模型学的不好）

                 

 

5.损失函数

    损失函数，可以评估学习到的规则好不好的衡量标准，比如上面把一张图片是猫的判定成了狗，那怎么衡量这个模型错误的程度呢，又有一张图片也是猫，同样预测为狗，但是猫这个类别的预测值是400，那这次的错误程度是怎么样，所有的东西都需要用数学计算出一个值，来表示程度。

   一般会采用一种方式来衡量，预测对的情况和预测错的情况之间的差距，就是损失函数。损失函数可以有很多种，这里展示了一个SVM的损失函数，这个方式是对于每一种错误的类别和正确类别之间的差值来衡量错误程度，比如一张图片，预测为猫的值是3.2，预测为车的值是5.1，预测为青蛙的值是-1.7，正确类别为猫，那么分别计算猫和车的误差，猫和青蛙的误差，最终误差和就是改成预测的损失函数，损失程度越大，说明误差越大，模型的效果越不好。

• svm损失函数
  • 计算每个错误类别和正确类别之间的差距的和（小于零取0值）
  • Li 越大，效果越差
  • 评估的是权重参数，权重即重要程度

                        

 

6. sigmoid函数 vs  softmax分类器

    一般对于深度学习的分类问题，一般都是多分类，一般会采用sigmoid函数或者softmax分类器，不管输入是什么样的值，我们期望得到的一个0-1之间的概率值。

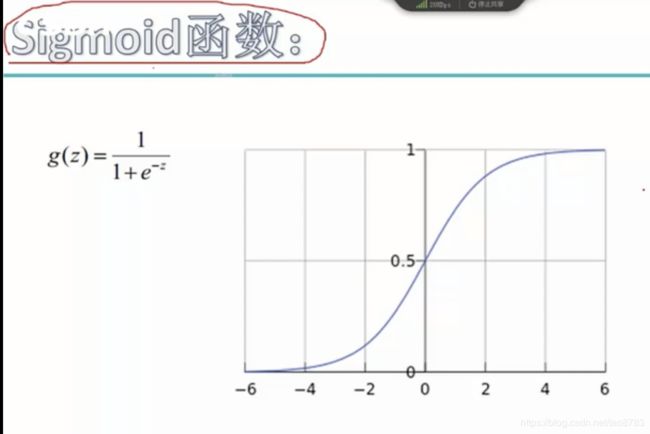
    对于sigmoid函数刚好有这个功能，可以将任意值，转换成0到1之间的小数，也是概率值。而且对于sigmoid函数来说，当x越接近于0的时候，梯度越大，越快收敛，这也是很多模型使用sigmoid函数，学习率一般都会调整为很小值的原因。

• sigmoid函数：x越接近于0，梯度越大；x越大，梯度越接近于0

      

• softmax分类器：
  • 输出：概率
  • 步骤：
    • 第一步exp：放大差异
    • 第二步归一化：希望输出的是概率
    • 第三步-log：交叉熵，希望归一化的概率越接近于1，loss越小，表示分对损失值小；归一化的概率越接近于0，loss越大，表示分错损失值大，交叉熵可以达到这样效果

       softmax是另外一种计算方式，softmax的想法是先把计算出来的值放大差异，然后对于所有的类别计算各自占的比重，否则单纯数值多少并不能反映每个类别预测对还是预测错的程度，我们期望的是正确类别的预测值，同时错误类别预测值越小越好，所以正确类别预测值占所有类别预测值的比重最能代表我们的期望。

     这时引入交叉熵，最终输出Li是损失程度，我们期望正确概率越接近于1，我们得到的损失loss越小越好，目前归一化后的值和我们期望的刚好相反，所以引入交叉熵，可以达到我们的预期，正确类别归一化的值为大(接近于1），损失loss越小（接近于0）。这是为了达到预期，人为的引入一些计算方式，来达到我们的效果。

    交叉熵也可以理解为信息量，输入概率值越大，越可能发生，信息量越小；输入概率小，越不可能发生，一旦发生携带的信息量越大。